Активное и пассивное давление грунтов на подпорные стены. – 115
Активным давлением называется давление грунта на конструкцию (подпорную стенку). В этом случае конструкция воспринимает давление грунта и может получить наиболее вероятные смещения (1, 2), обозначенные на нижнем рисунке с левой стороны. Пассивное давление или отпор в грунте возникает тогда, когда конструкция оказывает давление на грунт (опорный фундамент арки). Такая схема работы основания представлена на нижнем рисунке с правой стороны. Схема воздействия активного давления грунта на подпорную стенку и возникновения пассивного отпора при давлении фундамента на грунт. Определение величин активного давления грунта и пассивного отпора является одной из важнейших задач механики грунтов при решении ряда инженерных задач, и, прежде всего, устойчивости подпорных стен.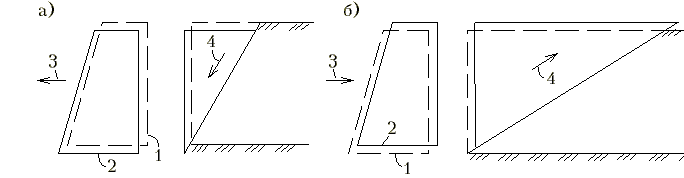 
Давление грунта на стену:а - активное; б - пассивное:1 - положение до начала перемещения стены; 2 - положение после перемещения стены; 3 - напрваление перемещения стены;
Аналитический метод расчета давления грунта на жесткую подпорную стену (грунт связанный, стена вертикальная, на поверхность засыпки пригрузка). – 116
В данном разделе рассмотрим аналитический метод определения давления грунтов на подпорные стенки при допущении плоских поверхностей скольжения. Этот метод в настоящее время наиболее широко применяется в практике проектирования.
Рассмотрим вначале давление на подпорные стенки сыпучих масс. Как было показано ранее, массив сыпучего грунта, ограниченный откосом, будет находиться в равновесии, если угол откоса равен углу внутреннего трения грунта. При вертикальном же откосе для удержания массива в равновесии требуется устройство подпорной стенки.
|
|
|
Если одна часть массива сыпучего грунта перемешается относительно другой по некоторой поверхности скольжения, то реакция неподвижной части массива будет направлена навстречу движению под углом трения, отложенным от нормали к поверхности скольжения. Рассмотрим наиболее характерные случаи давления грунтов на подпорные стенки.
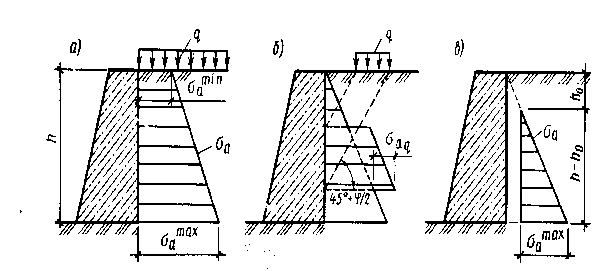
Основной случай — вертикальная гладкая стенка с горизонтальной поверхностью засыпки (рис. 162). Будем считать, что стенка жесткая и неподвижная; трением грунта о
стенку пренебрегаем. При сделанных ограничениях напряженное состояние грунта за подпорной стенкой будет совершенно одинаково с напряженным состоянием бесконечно распространенного слоя грунта. Для решения вопроса о давлении грунта на стенку можно применить следующий метод. Так как поверхность грунта горизонтальна, то горизонтальная площадка, выделенная на некоторой глубине от незагруженной поверхности грунта, будет испытывать только сжимаюшее давление (нормальное главное напряжение!), которое в рассматриваемом случае разно произведению объемного веса грунта на высоту столба грунта от поверхности до рассматриваемой площадки, т. е. Gi=yz
|
|
|
где у— объемный вес грунта; z — глубина рассматриваемой точки от горизонтальной поверхности засыпки.
Боковое дазление грунта при гладкой вертикальной стенке будет разно наименьшему главному напряжению сь при действии собственного веса грунта как сплошной нагрузки.
Обозначим боковое давление через и для определения его воспользуемся соотношением между главными напряжениями соответствующим состоянию предельного равновесия
грунта за подпорной стенкой, соответствующего возникновению поверхностей скольжения.
Действительно будет уравнение (44й )*. т. е.
Из уравнения (б)
°2 = °1 tg2(41°- "7")
а0 = о
или. подставляя значение а: из выражения (а), получим
3 случае же пассивного давления грунта, т. е. когда верх стенки будет перемешаться по направлению к грунту, аналогично предыдущему получим
Рис. 4. Зависимость пассивного давления от перемещения стены
Определение предельных значений давления грунта на вертикальные стены.
|
|
|
Предельные значения давления грунта на вертикальные стены, вызванные удельным весом, равномерной вертикальной поверхностной нагрузкой q и сцеплением с могут быть определены по формулам:
активное предельное состояние
sa(z) = Ka;h × [gz + q] – 2c√Kah ;
gta(z) = sa × tgd + a (положительно для движения грунта вниз);
пассивное предельное состояние
sp(z) = Kp;h × [gz + q] + 2c√Kph ;
tp(z) = sp × tgd+ a (положительно для движения грунта вверх),
где Ka;h и Kp;h – соответственно, коэффициенты горизонтального активного и пассивного давления;
s(z) и t(z) – нормальные и касательные напряжения на глубине z;
d – угол сопротивления сдвигу грунта по стене.
Приводятся графики для определения коэффициентов Ka;h и Kp;h. На рис. 2 и 3 приведены графики для совершенно гладкой стены (d = 0).
Дата добавления: 2018-02-15; просмотров: 3877; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!