Разобранные способы решения уравнений с модулями записать в тетрадь (примеры 5,6).
Классная работа
Метод интервалов для непрерывных функций
1) Вспомнить, как решаются уравнения с модулями. Разобранные способы решения уравнений с модулями записать в тетрадь (примеры 5,6).
1. Простейшими уравнениями с модулем являются уравнения вида 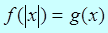 , (1)
, (1)
2. где 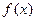 и
и 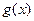 - некоторые функции.
- некоторые функции.
Для того чтобы решить данное уравнение, нужно найти сначала все решения уравнения 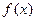 =
= 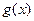 , принадлежащие множеству
, принадлежащие множеству 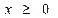 , затем решить уравнение
, затем решить уравнение 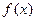 =
= 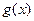 на множестве
на множестве 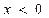 ; объединение множеств найденных решений составляет множество всех решений уравнения (1). Другими словами, уравнение (1) равносильно совокупности систем
; объединение множеств найденных решений составляет множество всех решений уравнения (1). Другими словами, уравнение (1) равносильно совокупности систем
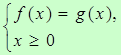 или
или 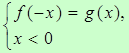
Пример 1.
Решите уравнение 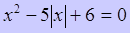 .
.
Решение.
Исходное уравнение равносильно совокупности систем:
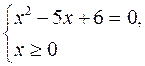 или
или 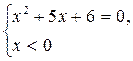 (1*)
(1*)
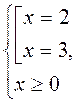 или
или 
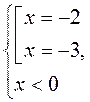
Ответ:  - 3; - 2; 2; 3.
- 3; - 2; 2; 3.
3. Уравнение вида 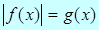 равносильно совокупности систем
равносильно совокупности систем 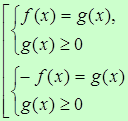
Пример 2.
Решите уравнение 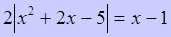
Решение.
Данное уравнение равносильно совокупности систем:
1) 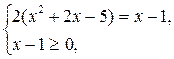
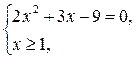
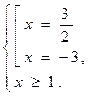
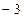 не удовлетворяет условию
не удовлетворяет условию 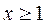 , следовательно, система имеет решение
, следовательно, система имеет решение  .
.
2)
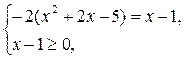
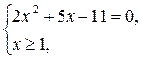
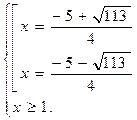
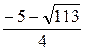 не удовлетворяет условию
не удовлетворяет условию 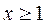 , следовательно, вторая система имеет решение
, следовательно, вторая система имеет решение 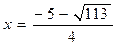 .
.
Ответ: 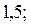
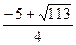 .
.
4. Уравнение вида 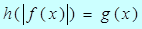 , где
, где 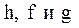 - некоторые функции, равносильно совокупности систем
- некоторые функции, равносильно совокупности систем
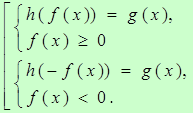
Пример 3.
Решите уравнение 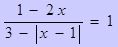
Решение.
Данное уравнение равносильно совокупности двух систем:
1) 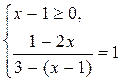
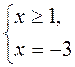 , система не имеет решений.
, система не имеет решений.
|
|
|
2) 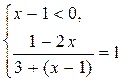
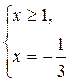 ,
, 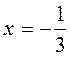 .
.
Ответ: 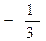
5. При решении уравнения, в котором под знаком модуля находится выражение, содержащее модуль, следует сначала освободиться от внутренних модулей, а затем в полученных уравнениях раскрыть оставшиеся модули.
Пример 4.
Решите уравнение 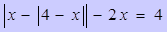 .
.
Решение.
Данное уравнение равносильно совокупности двух систем
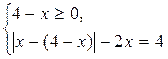 или
или 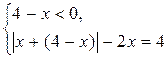
то есть совокупности систем
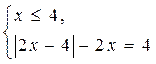 или
или 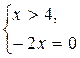
Вторая система решений не имеет. Первая система равносильна двум следующим системам:
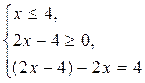 или
или 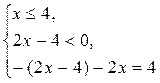
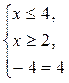 или
или 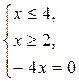
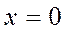
Ответ: 0.
5.Метод разбиения на промежутки. Уравнение вида 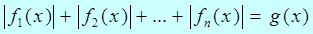 (2)
(2)
Решается методом интервалов (или методом разбиения на промежутки).
1. Найдем ОДЗ: х- любое (этот пункт можно опустить, как в примере 3, учитывать ОДЗ при решении уравнения без модуля)
2. Найдем нули всех подмодульных функций
Для этого находят все точки, в которых
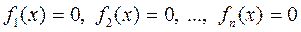
Эти точки делят область допустимых значений уравнения (2) на промежутки, на каждом из которых все функции 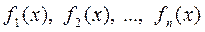 сохраняют знак (считаем знак каждого модуля на указанном промежутке).
сохраняют знак (считаем знак каждого модуля на указанном промежутке).
3. Отметим нули на ОДЗ и разобьем ОДЗ на интервалы
4. Найдем решение в каждом интервале (и проверим, входит ли решение в этот интервал)
Пример 5.
Решите уравнение 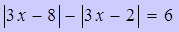 .
.
|
|
|
Решение.
1. Найдем ОДЗ: х- любое
2. Найдем нули всех подмодульных функций
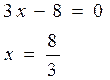
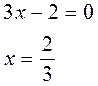
3. Отметим нули на ОДЗ и разобьем ОДЗ на интервалы
- - - + ++


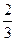
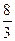
4. Найдем решение в каждом интервале (и проверим, входит ли решение в этот интервал)
1) 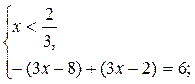
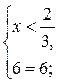
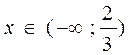
2) 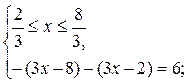
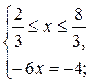
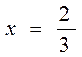
3) 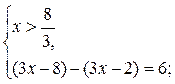
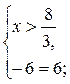
Ответ: 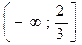
Пример 6.
Решите уравнение 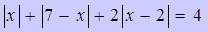 .
.
Решение.
1. Найдем ОДЗ: х- любое
2. Найдем нули всех подмодульных функций
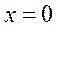
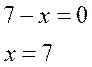
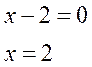
3. Отметим нули на ОДЗ и разобьем ОДЗ на интервалы
- + - + + - +++ +-+

0 2 7
1) 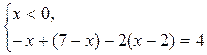
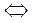
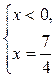 нет решений.
нет решений.
2) 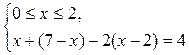
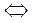
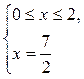 нет решений.
нет решений.
3) 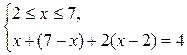
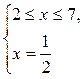 нет решений.
нет решений.
4) 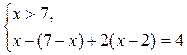
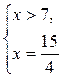 нет решений.
нет решений.
Ответ: корней нет.
Разобранные способы решения уравнений с модулями записать в тетрадь (примеры 5,6).
2) Разобрать уравнение под буквой ж) записать в тетрадь 
3) Прочитать п. 12.3. Вспомнить схему решения неравенств методом интервалов:
Найти ОДЗ
2. Найти нули функции f ( x ) [ f ( x )=0]
Дата добавления: 2021-06-02; просмотров: 45; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
