Знакопеременные и знакочередующиеся ряд. Абсолютная и условная сходимость. Признак сходимости Лейбница для знакочередующихся рядов
Числовые ряды
Понятие числового ряда
При изучении многих практических вопросов естествознания и техники применяется метод поэтапного исследования данного объекта. На первом этапе учитываются самые главные характеристики изучаемого процесса, явления - как говорят, выполняется этап первого приближения. Потом переходят к следующему этапу, учитывая новые или более точно старые характеристики предмета, и т.д.
Одним из математических понятий, при помощи которых моделируются такие ситуации, является понятие «суммы» бесконечного числа слагаемых, за которым утвердилось название ряда.
Числовым рядом называется сумма вида
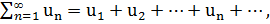 (1)
(1)
где числа 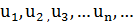 , называемые членами ряда, образуют бесконечную последовательность; член
, называемые членами ряда, образуют бесконечную последовательность; член  называется общим членом ряда.
называется общим членом ряда.
Суммы
S1= u1,
S2= u1+ u2,
S3= u1+ u2+u3,
…
Sn=u1+u2+u3+…+un,
составленный из первых членов ряда (1), называются частичными суммами этого ряда.
Каждому ряду можно сопоставить последовательность частичных сумм S1, S2, S3, …, Sn,.. Если при бесконечном возрастании номера n частичная сумма ряда Sn стремится к пределу S, то ряд называется сходящимся, а число S – суммой сходящегося ряда, т.е.
 или
или 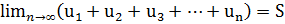
Эта запись равносильна записи

Если частичная сумма 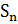 ряда (1) при неограниченном возрастании n не имеет конечного предела , то такой ряд называется расходящимся.
ряда (1) при неограниченном возрастании n не имеет конечного предела , то такой ряд называется расходящимся.
|
|
|
Если ряд сходится, то значение Sn при достаточно большом n является приближенным выражением суммы ряда S.
Разность rn= S - Sn называется остатком ряда. Если ряд сходится, то его остаток стремится к нулю, т. е. 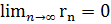 , и наоборот, если остаток стремится к нулю, то ряд сходится.
, и наоборот, если остаток стремится к нулю, то ряд сходится.
Признаки сходимости рядов
Необходимый признак сходимости ряда. Ряд  может сходиться только при условии, что его общий член un при неограниченном увеличении номера n стремится к нулю:
может сходиться только при условии, что его общий член un при неограниченном увеличении номера n стремится к нулю: 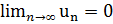 .
.
Если  , то ряд
, то ряд  расходится – это достаточный признак расходимости ряда.
расходится – это достаточный признак расходимости ряда.
Достаточные признака сходимости ряда с положительными членами.
а) Признак сравнения рядов с положительными членами. Исследуемый ряд сходится, если его члены не превосходят соответствующих членов другого, заведомо сходящегося ряда; исследуемый ряд расходится, если его члены превосходят соответствующие члены другого заведомо расходящегося ряда.
При исследовании рядов на сходимость и расходимость по этому признаку часто используется геометрический ря
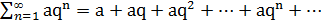 (a>0),
(a>0),
который сходится при 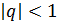 и расходится при
и расходится при 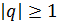 , и гармонический ряд
, и гармонический ряд
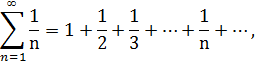
являющийся расходящимся.
При исследовании рядов используется также обобщенный гармонический ряд
|
|
|
1+ 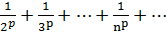 .
.
Если р=1, то данный ряд обращается в гармонический ряд, который является расходящимся.
Если р<1, то члены данного ряда больше соответствующих членов гармонического ряда и, значит, он расходится. При р>1 имеем геометрический ряд, в котором 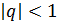 ; он является сходящимся. Итак, обобщенный гармонический ряд сходится при р>1 и расходится при р≤1.
; он является сходящимся. Итак, обобщенный гармонический ряд сходится при р>1 и расходится при р≤1.
б) Признак Даламбера. Если для ряда с положительными членами
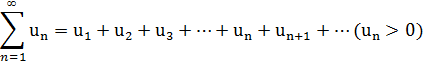
выполняется условие 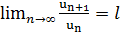 , то ряд сходится при l<1 и расходится при l>1.
, то ряд сходится при l<1 и расходится при l>1.
Признак Даламбера не дает ответа, если l=1. В этом случае исследования ряда применяются другие приемы.
Пример 1. Исследовать сходимость ряда, применяя необходимый признак сходимости:

Решение. Имеем
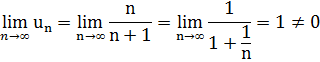
Здесь выполняется достаточный признак расходимости ряда; следовательно, ряд расходится.
Пример 2. Исследовать сходимость ряда, используя признак Даламбера:

Решение. Подставив в общий член ряда 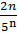 вместо n число n+1, получим
вместо n число n+1, получим 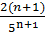 . Найдем предел отношения (n+1) – го члена к n –му члену при n→∞:
. Найдем предел отношения (n+1) – го члена к n –му члену при n→∞:

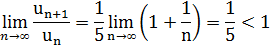
Следовательно, данный ряд сходится.
Знакопеременные и знакочередующиеся ряд. Абсолютная и условная сходимость. Признак сходимости Лейбница для знакочередующихся рядов
|
|
|
Числовой ряд
u 1 + u 2 + u 3 +…+ un +… (2)
называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные числа.
Числовой ряд (2) называется знакочередующимся, если любые два стоящие рядом члена имеют противоположные знаки. Этот ряд является частным случаем знакопеременного ряда.
Признак сходимости Лейбница для знакочередующихся рядов. Если члены знакочередующегося ряда (2) монотонно убывают по абсолютной величине и общий член un стремится к нулю при n →∞, то ряд (2) сходится.
Этот признак служит достаточным признаком сходимости знакочередующихся рядов.
Знакопеременный ряд (2) называется абсолютно сходящимся, если сходится ряд
│ u 1 │+│ u 2 │+│ u 3 │+…+│ un │+… (3)
составленный из абсолютных величин его членов, т.е. всякий абсолютно сходящийся ряд является сходящимся.
Если знакопеременный ряд (2) сходится, а составленный из абсолютных величин его членов ряд (3) расходится, то данный ряд (2) называется условно (неабсолютно) сходящимся. Заметим, что из расходимости ряда (3) в общем случае не следует расходимость ряда (2).
|
|
|
Пример 3. Исследовать на сходимость (абсолютную и условную) знакочередующийся ряд:

Решение. Члены данного ряда по абсолютной величине монотонно убывают: 1>  и
и 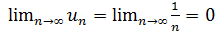 . Следовательно, согласно признаку Лейбница, ряд сходится. Выясним, сходится ли этот ряд абсолютно или условно.
. Следовательно, согласно признаку Лейбница, ряд сходится. Выясним, сходится ли этот ряд абсолютно или условно.
Ряд
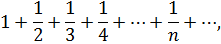
составленный из абсолютных величин членов данного ряда, является гармоническим рядом, который, как известно, расходится. Поэтому данный ряд сходится условно.
Пример 4. Исследовать сходимость знакопеременного ряда

Решение. Составим ряд из абсолютных величин членов данного ряда:
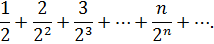
Для исследования этого ряда применим признак Даламбера. Имеем
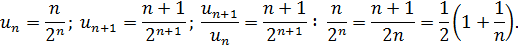

Ряд, составленный из абсолютных величин, сходится; следовательно, данный знакопеременный ряд сходится абсолютно. [1]
Упражнения для закрепления
1. Найдите первые четыре члена ряда по заданному общему члену:
а)  b)
b) 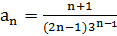
2. Найдите формулу общего члена ряда:
3. а)  б)
б) 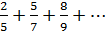
4. Используя признак Лейбница; исследуйте сходимость знакочередующегося ряда: а)  ;
;
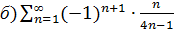
5. Используя признак Даламбера, исследуйте сходимость ряда 
Контрольные вопросы
1. Дайте определение числового ряда.
2. Какую сумму называют частичной суммой ряда?
3. Какой ряд называется сходящимся? расходящимся?
4. Сформулируйте признак Даламбера.
Дата добавления: 2021-06-02; просмотров: 203; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
