Разложение некоторых элементарных функций в ряд Маклорена
Лекция 6. Ряд Тейлора. Необходимое и достаточное условие разложения. Разложения основных элементарных функций
Разложение функций в степенные ряды. Ряд Тейлора
Представление функции в виде суммы степенного ряда или, иными словами, разложение функции в степенной ряд имеет важное теоретическое и практическое значение.
Определение 7.1. Функция 
в некоторой окрестности 
, 
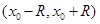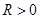, точки 
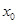разлагается в степенной ряд 
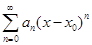если в этой окрестности данный степенной ряд сходится и его сумма равна , т.~е.
Определение 7.2. Пусть функция бесконечно дифференцируема в некоторой окрестности точки 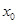. Ряд
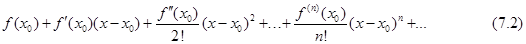
называется рядом Тейлора функции в точке .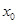
Теорема 7.1. Пусть функция в некоторой окрестности точки 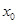разлагается в степенной ряд 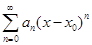, т.~е. для всех 
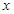из упомянутой окрестности справедливо равенство
Тогда этот степенной ряд определяется однозначно и является рядом Тейлора функции , то есть коэффициенты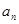 
данного степенного ряда находятся по формулам Тейлора
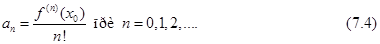
Доказательство
В силу следствия 6.1 функция бесконечно дифференцируема в окрестности точки 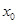и имеет место равенство
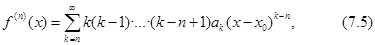
где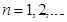 
В последнем равенстве, полагая 
,получим
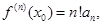
а следовательно,
Что и требовалось доказать.
Итак, доказано, что если функция в некоторой окрестности точки 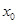разлагается в степенной ряд, то этот ряд является рядом Тейлора функции и, стало быть, это разложение единственное:
|
|
|
Поскольку ряд Тейлора можно составить для произвольной бесконечно дифференцируемой в окрестности точки 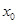функции, то возникает естественный вопрос: является лиряд Тейлора функции сходящимся в рассматриваемой окрестности точки 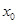, и если да, то будет ли его сумма равна ? Как показывает следующий пример, ответ на этот вопрос в общем случае отрицательный.
Пример 7.1. Исследовать сходимость ряда Тейлора функции
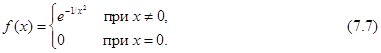
Данная функция бесконечно дифференцируема на всей оси 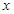, причем
т.~е. все коэффициенты ряда Тейлора рассматриваемой функции в точке 
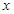равны нулю. Следовательно, ряд Тейлора этой функции в точке сходится на всей оси и его сумма равна нулю, в то время как данная функция не нулевая.
Таким образом, показано, что функция , определенная формулой (7.7), не разлагается в ряд Тейлора в точке . Необходимо найти условия, при которых функция разлагается в ряд Тейлора.
Теорема 7.2. Пусть бесконечно дифференцируемая в некоторой окрестности точки 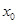функция. Для того, чтобы функцию в этой окрестности можно было разложить в ряд Тейлора, необходимо и достаточно, чтобы остаточный член в формуле Тейлора
|
|
|
стремился к нулю для всех точек указанной окрестности, когда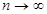 
:
Доказательство Необходимость. Пусть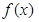 
разлагается в ряд Тейлора в некоторой окрестности точки 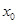, т.~е. имеет место разложение (7.6). Это означает, что разность между суммой и частичной суммой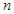 
-го порядка ряда (7.6), равная, согласно (7.8), остаточному члену 
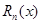в формуле Тейлора, стремится к нулю, при 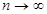и для всех точек из рассматриваемой окрестности точки .
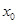Достаточность. Предположим, что имеет место равенство (7.9):
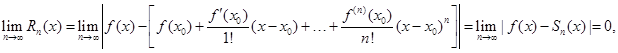
где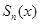 
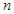- -частичная сумма ряда (7.6). Значит, ряд Тейлора (7.6) сходится и его сумма равна , то есть разлагается в ряд Тейлора.
Следующее достаточное условие разложимости функций в ряд Тейлора имеет большое практическое значение и охватывает ряд важных случаев.
Теорема 7.3. Пусть в некоторой окрестности точки 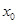функция имеет производные всех порядков. Если существует такая постоянна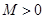 
, что
при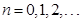 
и для всех 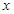из указанной окрестности точки 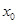, то функция разлагается в ряд Тейлора в этой окрестности.
Доказательство Согласно теореме 7.2, достаточно доказать, что остаточный член 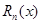в формуле Тейлора (7.8) стремится к нулю, при 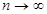и для всех точек из рассматриваемой окрестности точки 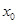. В самом деле, представив в форме Лагранжа дополнительный член 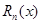, в силу (7.10) получим следующую оценку:
|
|
|
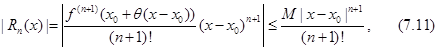
где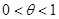 
.
С помощью признака Даламбера легко убедиться, что ряд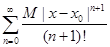 
сходится, поэтому, в силу необходимого признака сходимости, общий член этого ряда стремится к нулю, при :
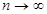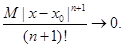
Значит, согласно оценкe (7.11),
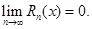
Что и требовалось доказать.
Чаще всего приходится иметь дело со случаем, когда и функция разлагается в ряд непосредственно по степеням :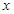
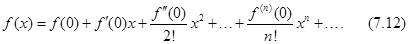
Этот ряд называется рядом Маклорена функции .
Разложение некоторых элементарных функций в ряд Маклорена
Теорема 7.3 охватывает ряд важных случаев.
I. Эта теорема непосредственно применима к функциям 
, 
, 
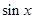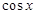в любом интервале 
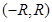. Действительно,
Итак, функции , 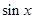и 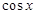разлагаются в ряд Тейлора по степеням 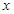. Вычисляя коэффициенты Тейлора 
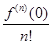этих функций, получим разложения
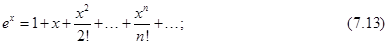
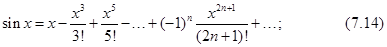
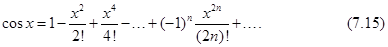
II. Как уже было установлено в примере 6.1 функции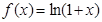 
и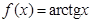 
разлагаются в ряд Маклорена следующим образом:
При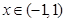 
;
при .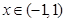
Замечание 7.1. Разложение (7.16) остается справедливым и при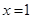 
. Следовательно,
Замечание 7.2. Разложение (7.17) также справедливо при 
. При этом имеем
Разложения (7.18) и (7.19) можно использовать для вычисления чисел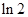 
и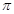 
с любой степенью точности. В качестве приближенных значений этих чисел можно брать частичные суммы рядов (7.18) и (7.19). При этом, в силу признака Лейбница, допущенная погрешность не превзойдет первого из отброшенных членов.
|
|
|
Дата добавления: 2021-06-02; просмотров: 68; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!