Критерий Найквиста часто используется для логарифмических частотных характеристик.

Частотные критерии устойчивости

Это графоаналитические методы, позволяющие по виду частотных характеристик САУ судить об их устойчивости. Их общее достоинство в простой геометрической интерпретации, наглядности и в отсутствии ограничений на порядок дифференциального уравнения.

Критерий Найквиста Этот критерий позволяет судить об устойчивости замкнутой САУ по виду АФЧХ разомкнутой САУ .Исследование разомкнутой САУ проще, чем замкнутой.

Критерий Найквиста позволяет определить устойчивость замкнутой системы, построив

частотную характеристику разомкнутой системы.

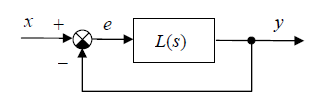
Пусть L(s) – передаточная функция разомкнутой системы, а L( jω) – ее частотная характеристика.

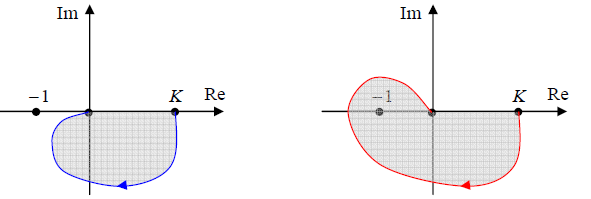
Годограф Найквиста– некоторая кривая, которая начинается в точке (K; 0) на вещественной оси и заканчивается в начале координат (если L(s) – строго правильная функция, то есть степень ее числителя меньше степени знаменателя).

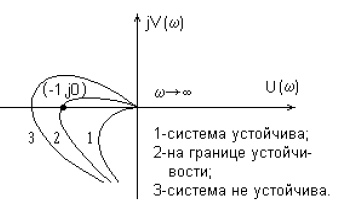
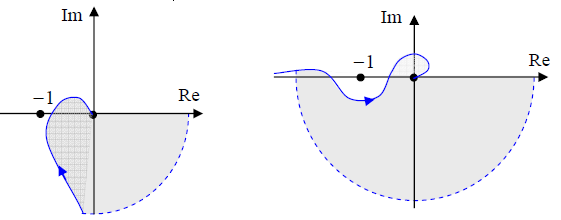
Можно доказать, что система устойчива тогда и только тогда, когда годограф L( jω) не охватывает точку (−1; 0) . На рисунке слева годограф не охватывает эту точку (и замкнутая система устойчива), а на рисунке справа – охватывает (система неустойчива).

Выражение «система находится на границе устойчивости» означает, что частотная характеристика проходит через точку (−1; 0) . В этом случае для некоторой частоты ω мы имеем A(ω) =1 и φ (ω) = −180° . Это говорит о том, что после прохождения контура величина сигнала меняет знак, сохраняя абсолютную величину (энергию), то есть устанавливаются незатухающие колебания.

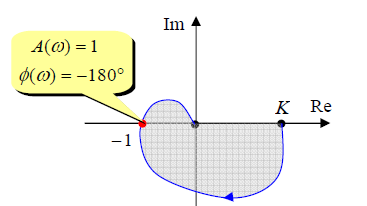
Частота ωс, для которой A (ωc) = 1, называется частотой среза. Для устойчивой системы значение фазы на частоте среза должно быть больше, чем −180; в этом случае годограф не охватит точку (−1; 0) .

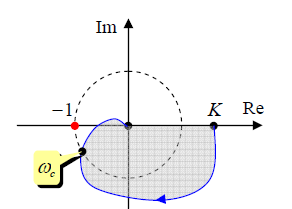
2.Если передаточная функция L(s) имеет полюса в точке s = 0 (то есть обращается в бесконечность в этой точке), ситуация усложняется. Теперь годограф начинается не на вещественной оси, а приходит из бесконечности. Тогда в контур необходимо включить не только полученную кривую, но и часть окружности бесконечного радиуса от вещественной оси до годографа в порядке обхода по часовой стрелке. Если функция L(s) имеет k полюсов в точке s = 0,нужно добавить k секторов по 90° . На рисунках показаны годографы Найквиста устойчивых систем, в которых функция L(s) имеет соответственно 1 и 2 полюса в точке s = 0. Эти годографы не охватывают точку (−1; 0) .

Если в системе есть запаздывание на время τ , на любой частоте появляется дополнительный сдвиг фазы на −τω (без изменения амплитуды). Это значит, что каждая точка годографа поворачивается на некоторый угол против часовой стрелки.

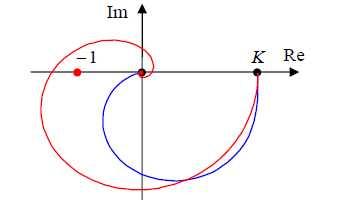
На рисунке синяя линия – частотная характеристика системы без запаздывания, а крас-

ная – аналогичная характеристика для системы с запаздыванием. Видно, что запаздывание привело к неустойчивости системы (годограф охватил критическую точку (−1; 0) ). Таким образом,система может потерять устойчивость из-за «медленного» датчика. Можно говорить о том, что запаздывание всегда ухудшает устойчивость системы, и этот факт важно учитывать при проектировании.

Если L(s) имеет полюса с положительной вещественной частью (разомкнутая система неустойчива) , нужно считать, сколько раз годограф пересекает ось абсцисс левее точки ( − 1; 0) . Причем переходы «сверху вниз» считаются положительными, а переходы «снизу вверх» - отрицательными

Для того, чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы раз-

ница между числом положительных и отрицательных переходов была равна l / 2 , где l – число неустойчивых полюсов функции L(s) . Начальная точка на оси абсцисс левее точки (−1; 0) считается за половину перехода. На рисунке показаны годографы устойчивых систем для случая l = 1.

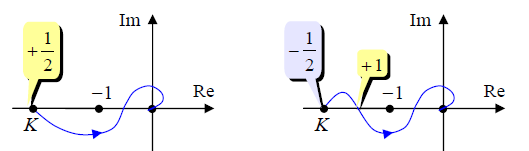
Частотная характеристика начинается на вещественной оси левее точки (−1; 0) . На рисун-

ке слева годограф сначала идет вниз (половина положительного перехода) и больше нигде не пересекает ось абсцисс левее точки (−1; 0) , поэтому разница переходов равна 1/ 2 = l / 2 и замкнутая система устойчива.

На правом рисунке частотная характеристика сначала идет вверх (считаем это за половину

отрицательного перехода), а затем переходит в нижнюю полуплоскость (положительный переход). Разница снова равна 1/ 2 = l / 2 и система устойчива.

Критерий Найквиста часто используется для логарифмических частотных характеристик.

Сначала предположим, что передаточная функция разомкнутой системы не имеет неустойчивых полюсов. Как мы уже знаем, для анализа устойчивости наиболее важно поведение частотной характеристики в районе частоты среза

ωc, где A (ωc) = 1 и Для устойчивой системы значение фазы на частоте среза должно быть больше, чем − 180 ° . На графике представлены три фазовых характеристики устойчивых систем. Кривая 1 соответствует случаю, когда в разомкнутой системе нет интеграторов (и фазовая характеристика начинается с нуля), кривая 2 – системе с одним интегратором, а кривая 3 – c двумя.

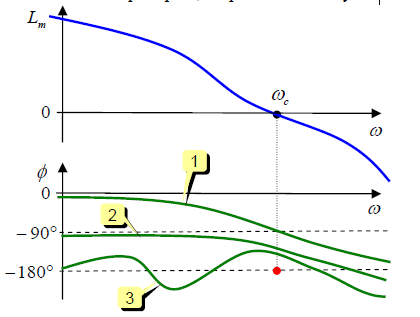
Если разомкнутая система имеет неустойчивые звенья, нужно считать переходы фазовой

характеристики через линию φ (ω) = −180° левее частоты среза. Здесь положительным считается переход снизу вверх, а отрицательным – сверху вниз. Если фазовая характеристика начинается на линии φ (ω) = −180° (на нулевой частоте), это считается за половину перехода. Для устойчивой системы разность между числом положительных и отрицательных переходов должна быть равна l / 2 , где l – число неустойчивых полюсов передаточной функции L(s) .

Достоинство . Критерий Найквиста очень нагляден. Он позволяет не только выявить, устойчива ли САУ, но и, в случае, если она неустойчива, наметить меры по достижению устойчивости.

Критерий устойчивости Михайлова

То есть САУ будет устойчива, если вектор D(j ) при изменении частоты от 0 до + 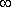повернется на угол n /2.

При этом конец вектора опишет кривую, называемую годографом Михайлова. Она начинается на положительной полуоси, так как D(0) = a _n, и последовательно проходит против часовой стрелки n квадрантов комплексной плоскости, уход в бесконечность в n - ом квадранте (рис.69а).

Если это правило нарушается (например, число проходимых кривой квадрантов не равно n, или нарушается последовательность прохождения квадрантов (рис.69б)), то такая САУ неустойчива - это и есть необходимое и достаточное условие критерия Михайлова.

Достоинства . Этот критерий удобен своей наглядностью. Так, если кривая проходит вблизи начала координат, то САУ находится вблизи границы устойчивости и наоборот. Этим критерием удобно пользоваться, если известно уравнение замкнутой САУ.

Контрольныевопросы

1. Что называется частотными критериями устойчивости САУ?

2. В чем преимущество частотных критериев устойчивости перед алгебраическими.

3. Сформулируйте критерий устойчивости Михайлова.

4. Сформулируйте критерий устойчивости Найквиста.

5. В чем особенность использования критерия Найквиста для астатических САУ?

Дата добавления: 2021-06-02; просмотров: 142; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!