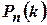Наиболее вероятное число успехов
Раздел «Повторение независимых испытаний»
Содержание
Тема 4. Схема независимых испытаний и формула Бернулли
Схема независимых испытаний Бернулли
Производится серия из 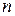 испытаний, удовлетворяющих следующим условиям:
испытаний, удовлетворяющих следующим условиям:
1) каждое испытание имеет два исхода (появление события 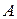 - «успех» и появление события «не-
- «успех» и появление события «не- 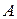 » =
» = 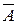 - «неудача») – взаимно несовместных и противоположных события;
- «неудача») – взаимно несовместных и противоположных события;
2) в каждом испытании вероятность появления события 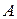 постоянна и равна
постоянна и равна 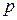 (
( 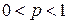 ), тогда вероятность события
), тогда вероятность события 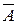 равна
равна 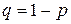 ;
;
3) все 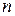 испытаний независимы, т.е. вероятность наступления события в любом из
испытаний независимы, т.е. вероятность наступления события в любом из 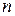 повторных испытаний не зависит от результатов других испытаний.
повторных испытаний не зависит от результатов других испытаний.
Такая схема называется последовательностью испытаний Бернулли, или схемой Бернулли.
Пример 1. Испытания Бернулли:
1) многократное подбрасывание монеты,
2) многократная стрельба по мишени,
3) проверка деталей на годность (для партии, содержащей достаточно большое количество деталей),
4) телефонные звонки по определенному номеру.
Теорема и формула Бернулли
Теорема. Вероятность того, что в схеме независимых испытаний Бернулли событие 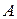 появится ровно
появится ровно 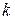 раз, вычисляется по формуле Бернулли
раз, вычисляется по формуле Бернулли
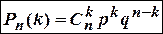 ,
,
где 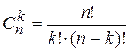 - биномиальный коэффициент.
- биномиальный коэффициент.
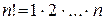 - факториал числа
- факториал числа 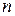 . Считается, что
. Считается, что 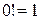 .
.
Вероятности 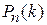 называются биномиальными.
называются биномиальными.
Названа в честь выдающегося швейцарского математика Якоба Бернулли, который вывел эту формулу.
|
|
|
Пример 2. Произведены четыре независимых выстрела по мишени. Вероятность попадания в мишень при одном выстреле равна 0,6. Найти вероятность того, что мишень будет поражена: 1) три раза; 2) ни разу.
Решение
Последовательность испытаний удовлетворяет всем условиям последовательности повторных независимых испытаний:
§ число испытаний конечно 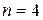 ;
;
§ каждое испытание заканчивается событием 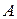 «попадание в мишень», либо
«попадание в мишень», либо 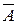 - «промах»;
- «промах»;
§ вероятность попадания при каждом выстреле 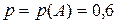 , тогда
, тогда 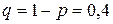 ;
;
§ все испытания независимы.
1) Применяя формулу Бернулли при 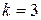 , получим:
, получим:
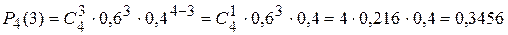 .
.
2) Применяя формулу Бернулли при 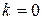 , получим:
, получим:
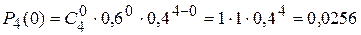 .
.
Вероятности сложных событий в схеме Бернулли для малого числа испытаний
1. Сумма вероятностей 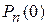 ,
, 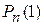 , …,
, …, 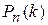 , …,
, …, 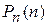 равна единице:
равна единице:
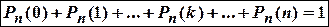 .
.
2. Вероятность того, что в последовательности 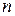 независимых испытаний событие
независимых испытаний событие 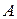 наступит:
наступит:
1) менее 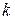 раз
раз 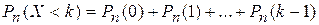 ;
;
2) более 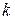 раз
раз 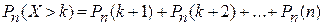 ;
;
3) не менее 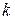 раз
раз 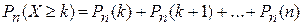 ;
;
4) не более 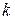 раз
раз 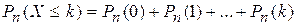 ;
;
5) от 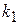 до
до 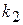 раз
раз 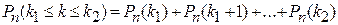 .
.
Пример 3. В условиях примера 2 найти вероятность того, что мишень будет поражена от одного до четырех раз.
Здесь 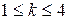 .
.
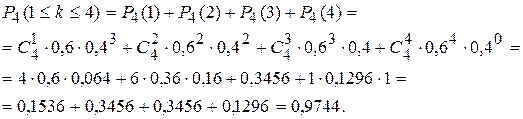
Пример 4. Найти вероятность того, что в четырех независимых выстрелах мишень будет поражена хотя бы один раз (см. пример 2).
|
|
|
Очевидно, что 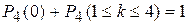 как вероятность достоверного события. Отсюда
как вероятность достоверного события. Отсюда 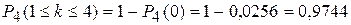 (вероятность
(вероятность 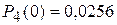 найдена в примере 2).
найдена в примере 2).
Наиболее вероятное число успехов
Наиболее вероятное число успехов в серии повторных независимых испытаний – это такое число 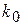 , при котором биномиальная вероятность
, при котором биномиальная вероятность 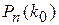 является наибольшей для данного числа испытаний
является наибольшей для данного числа испытаний 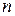 .
.
Таким образом, вероятность 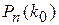 является наибольшей среди вероятностей
является наибольшей среди вероятностей 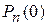 ,
, 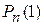 , …,
, …, 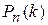 , …,
, …, 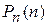 .
.
Наиболее вероятное число успехов удовлетворяет неравенству
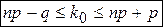 , или
, или 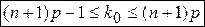 .
.
Отметим, что 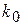 - целое число и может быть не единственным.
- целое число и может быть не единственным.
Пример 5. Найти наивероятнейшее число годных деталей среди 19 проверяемых, если вероятность детали быть годной, равна 0,9.
По условию задачи 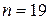 ,
, 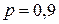 ,
, 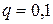 . Найдем целое число
. Найдем целое число 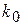 , удовлетворяющее неравенству:
, удовлетворяющее неравенству: 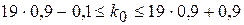 , или
, или 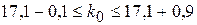 , или
, или 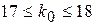 .
.
Это означает, что вероятности 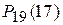 и
и 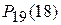 - наибольшие среди всех биномиальных вероятностей
- наибольшие среди всех биномиальных вероятностей 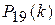 при
при 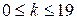 .
.
Наивероятнейшее число годных деталей равно 17 или 18. Другими словами, при заданных условиях среди 19 проверяемых деталей вероятнее всего будет 17 или 18 годных деталей.
Тема 5. Вычисление биномиальных вероятностей 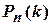 при большом числе испытаний
при большом числе испытаний
|
|
|
Локальная теорема Лапласа
Пусть проведено большое число 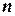 независимых испытаний Бернулли, причем выполняется условие
независимых испытаний Бернулли, причем выполняется условие 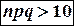 . Рекомендуемое минимальное количество испытаний – примерно 50-100.
. Рекомендуемое минимальное количество испытаний – примерно 50-100.
Теорема. При больших значениях 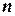 и не малых
и не малых 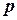 биномиальная вероятность
биномиальная вероятность 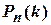 появления события
появления события 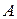
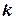 раз в
раз в 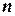 независимых испытаниях Бернулли приближенно вычисляется по формуле Лапласа
независимых испытаниях Бернулли приближенно вычисляется по формуле Лапласа
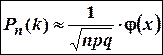 , где
, где 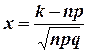 .
.
Функция 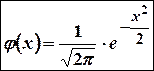 называется локальной (малой) функцией Лапласа. Ее значения приведены в таблице (Приложение 1).
называется локальной (малой) функцией Лапласа. Ее значения приведены в таблице (Приложение 1).
Локальная теорема Лапласа работает тем лучше, чем вероятность 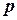 ближе к 0,5, и наоборот – даёт существенную погрешность при значениях
ближе к 0,5, и наоборот – даёт существенную погрешность при значениях 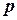 , близких к нулю либо единице.
, близких к нулю либо единице.

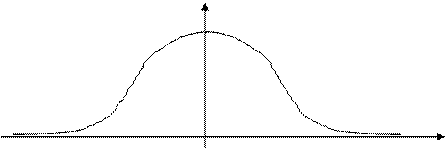
Свойства и график функции 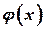
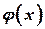
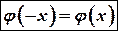
-5 0 5 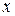
Свойства функции 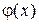
§ Функция 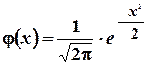 четная:
четная: 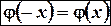 . Значит, ее график симметричен относительно оси ординат.
. Значит, ее график симметричен относительно оси ординат.
§ Функция 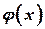 принимает только положительные значения. Значит, ее график выше оси абсцисс.
принимает только положительные значения. Значит, ее график выше оси абсцисс.
§ Если значения аргумента 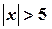 , то значение функции
, то значение функции 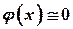 . Поэтому в таблице приведены значения функции
. Поэтому в таблице приведены значения функции 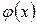 только для положительных значений аргумента от 0 до 5.
только для положительных значений аргумента от 0 до 5.
|
|
|
Пример 6. Найти вероятность того, что при 100 подбрасываниях монеты герб появится ровно 50 раз.
Событие 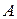 - появление герба при одном подбрасывании монеты,
- появление герба при одном подбрасывании монеты, 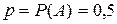 . По условию задачи
. По условию задачи 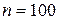 . Так как число испытаний достаточно велико, то искомую вероятность
. Так как число испытаний достаточно велико, то искомую вероятность 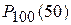 найдем по приближенной формуле Лапласа.
найдем по приближенной формуле Лапласа.
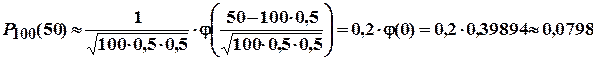 .
.
Значение 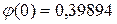 найдено по таблице в Приложении.
найдено по таблице в Приложении.
2. Вычисление 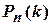 при больших
при больших 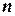 и малых
и малых 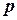 . Формула Пуассона
. Формула Пуассона
Теорема. Пусть число независимых испытаний Бернулли 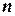 велико (
велико ( 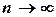 ), а вероятность появления «успеха»
), а вероятность появления «успеха» 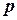 в каждом испытании мала (
в каждом испытании мала ( 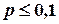 ).
).
Тогда для вычисления вероятности наступления ровно 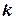 успехов
успехов 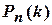 применяют приближенную формулу Пуассона
применяют приближенную формулу Пуассона
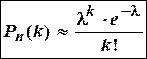 ,
,
где 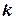 - число появления успеха в
- число появления успеха в 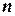 независимых испытаниях;
независимых испытаниях;
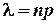 - среднее число появления успеха в
- среднее число появления успеха в 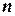 испытаниях.
испытаниях.
Значения функции Пуассона 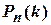 приведены в таблице (Приложение 3).
приведены в таблице (Приложение 3).
Пример 8. Телефонная станция обслуживает 400 абонентов. Для каждого абонента вероятность того, что в течение часа он позвонит на станцию, равна 0,01. Найти вероятность того, что в течение часа позвонят на станцию только один абонент.
Испытание – звонок на телефонную станцию – проводится 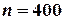 раз (велико). «Успех» - абонент позвонил, «неудача» – не позвонил.
раз (велико). «Успех» - абонент позвонил, «неудача» – не позвонил.
Вероятность 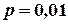 того, что абонент дозвонится в течение часа (успех) мала,
того, что абонент дозвонится в течение часа (успех) мала, 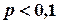 . Число одинаковых испытаний (звонки абонентов) велико
. Число одинаковых испытаний (звонки абонентов) велико 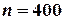 . Требуется найти вероятность
. Требуется найти вероятность 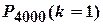 .
.
Для нахождения вероятности 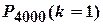 применим формулу Пуассона. Вычислим значение
применим формулу Пуассона. Вычислим значение 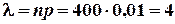 - это среднее количество абонентов, дозвонившихся на телефонную станцию в течение часа. Тогда вероятность
- это среднее количество абонентов, дозвонившихся на телефонную станцию в течение часа. Тогда вероятность  .
.
Схема применения формул вычисления биномиальных вероятностей 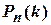
|
| |||||||||||||||
| Вероятность того, что событие А произойдет ровно
| |||||||||||||||
Условия
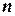 невелико, невелико,
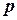 не мало не мало
| Условия
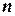 велико, велико,
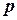 не мало ( не мало ( 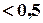 ), ),
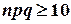
| Условия
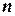 велико, велико,
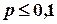
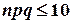
| |||||||||||||
Формула Бернулли
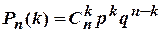
| Формула Лапласа
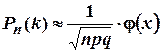
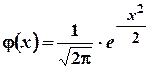 , ,
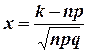
| Формула Пуассона
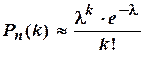 , ,
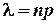
| |||||||||||||
Тема 6.Вычисление 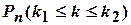 при большом числе испытаний
при большом числе испытаний
Ф ормула Муавра-Лапласа
Пусть проведено большое число 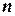 независимых испытаний Бернулли, причем выполняется условие
независимых испытаний Бернулли, причем выполняется условие 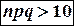 .
.
Тогда вероятность того, что число успехов находится в промежутке от 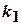 до
до 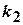 приближенно вычисляется по интегральной формуле Муавра-Лапласа
приближенно вычисляется по интегральной формуле Муавра-Лапласа 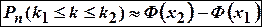 ,
,
где 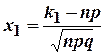 и
и 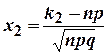 .
.
Функция
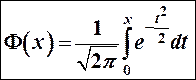
называется функцией Лапласа (интеграл вероятностей). Другое название – стандартная (или нормированная) функция Лапласа.
Ее значения приведены в таблице (Приложение 2).
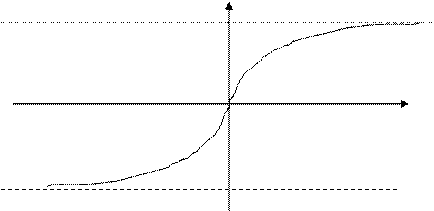
Свойства и график функции Лапласа 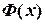
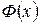
0,5
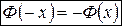
- 5 0 5 
-0,5
График функции Лапласа 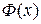
Свойства функции Лапласа 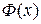
§ 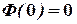 , т.е. график
, т.е. график 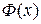 проходит через начало координат.
проходит через начало координат.
§ 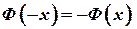 - нечетная функция, т.е. график
- нечетная функция, т.е. график 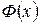 симметричен относительно начала координат.
симметричен относительно начала координат.
§ 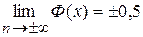 , значит, прямые
, значит, прямые 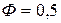 и
и 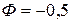 являются горизонтальными асимптотами. При
являются горизонтальными асимптотами. При 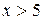 полагают
полагают 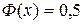 , а при
, а при 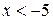 полагают
полагают 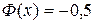 .
.

Пример 7. Найти вероятность того, что при 100 подбрасываниях монеты герб появится от 40 до 60 раз.
Решение
Здесь: 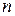 =100;
=100; 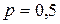 ;
; 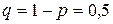 ;
; 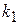 =40;
=40; 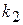 =60.
=60.
Найти вероятность 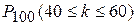 .
.
1) Проверим выполнение неравенства npq > 10 :
100*0,5*0,5=25 > 10 (выполняется).
Применим приближенную формулу Муавра Лапласа.
2) Вычислим значения
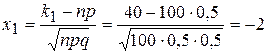 ;
; 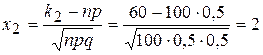 .
.
3) По таблице найдем значения
Ф(2) = 0,4772; тогда Ф(-2)= - Ф(2) = - 0,4772.
Здесь использовано свойство нечетности функции Лапласа 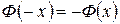 . Значение
. Значение 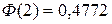 найдено по таблице.
найдено по таблице.
По формуле 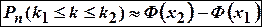 получим:
получим:
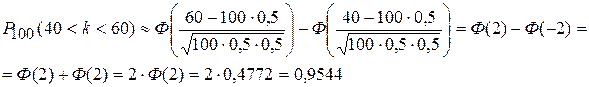
.ПРИЛОЖЕНИЯ


Таблица значений функции Пуассона: 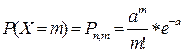
| m | a | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6. | 0.7 | 0.8 | 0.9 |
| 0 | 0.9048 | 0.8187 | 0.7408 | 0.6703 | 0.6065 | 0.5488 | 0.4966 | 0.4493 | 0.4066 | |
| 1 | 0.0905 | 0.1638 | 0.2222 | 0.2681 | 0.3033 | 0.3293 | 0.3476 | 0.3596 | 0.3639 | |
| 2 | 0.0045 | 0.0164 | 0.0333 | 0.0536 | 0.0758 | 0.0983 | 0.1217 | 0.1438 | 0.1648 | |
| 3 | 0.0002 | 0.0011 | 0.0033 | 0.0072 | 0.0126 | 0.0198 | 0.0284 | 0.0383 | 0.0494 | |
| 4 | - | 0.0001 | 0.0003 | 0.0007 | 0.0016 | 0.0030 | 0.0050 | 0.0077 | 0.0111 | |
| 5 | - | - | - | 0.0001 | 0.0002 | 0.0004 | 0.0007 | 0.0012 | 0.0020 | |
| 6 | - | - | - | - | - | - | 0.0001 | 0.0002 | 0.0003 | |
| m | a | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0. | 7.0 | 8.0 | 9.0 |
| 0 | 0.3679 | 0.1383 | 0.0498 | 0.0183 | 0.0067 | 0.0025 | 0.0009 | 0.0003 | 0.0001 | |
| 1 | 0.3679 | 0.2707 | 0.1494 | 0.0733 | 0.0337 | 0.0149 | 0.0064 | 0.0027 | 0.0011 | |
| 2 | 0.1839 | 0.2707 | 0.2240 | 0.1465 | 0.0842 | 0.0446 | 0.0223 | 0.0107 | 0.0050 | |
| 3 | 0.0613 | 0.1805 | 0.224 | 0.1984 | 0.1404 | 0.0892 | 0.0521 | 0.0286 | 0.0150 | |
| 4 | 0.0153 | 0.0902 | 0.1680 | 0.1954 | 0.1755 | 0.1339 | 0.0912 | 0.0572 | 0.0337 | |
| 5 | 0.0031 | 0.0361 | 0.1008 | 0.1563 | 0.1755 | 0.1606 | 0.1277 | 0.0916 | 0.0607 | |
| 6 | 0.0005 | 0.0120 | 0.0504 | 0.1042 | 0.1462 | 0.1606 | 0.1490 | 0.1221 | 0.0911 | |
| 7 | 0.0001 | 0.0034 | 0.0216 | 0.0595 | 0.1045 | 0.1377 | 0.1490 | 0.1396 | 0.1171 | |
| 8 | - | 0.0009 | 0.0081 | 0.0298 | 0.0655 | 0.1033 | 0.1304 | 0.1396 | 0.1318 | |
| 9 | - | 0.0002 | 0.0027 | 0.0132 | 0.0363 | 0.0689 | 0.1014 | 0.1241 | 0.1318 | |
| 10 | - | - | 0.0008 | 0.0053 | 0.0181 | 0.0413 | 0.0710 | 0.0993 | 0.1186 | |
| 11 | - | - | 0.0002 | 0.0019 | 0.0082 | 0.0255 | 0.0452 | 0.0722 | 0.0970. | |
| 12 | - | - | 0.0001 | 0.0006 | 0.0034 | 0.0113 | 0.0264 | 0.0481 | 0.0728 | |
| 13 | - | - | - | 0.0002 | 0.0013 | 0.0052 | 0.0142 | 0.0296 | 0.0504 | |
| 14 | - | - | - | 0.0001 | 0.0005 | 0.0022 | 0.0071 | 0.0169 | 0.0324 | |
| 15 | - | - | - | - | 0.0002 | 0.0009 | 0.0033 | 0.0090 | 0.0194 | |
| 16 | - | - | - | - | - | 0.0003 | 0.0015 | 0.0045 | 0.0109 | |
| 17 | - | - | - | - | - | 0.0001 | 0.0006 | 0.0021 | 0.0058 | |
| 18 | - | - | - | - | - | - | 0.0002 | 0.0009 | 0.0029 | |
| 19 | - | - | - | - | - | - | 0.0001 | 0.0004 | 0.0014 | |
| 20 | - | - | - | - | - | - | - | 0.0002 | 0.0006 | |
| 21 | - | - | - | - | - | - | - | 0.0001 | 0.0003 | |
| 22 | - | - | - | - | - | - | - | - | 0.0001 | |
Дата добавления: 2021-04-05; просмотров: 221; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!