ЭЛЕМЕНТАРНЫЕ ПРИЕМЫ И ИСПОЛЬЗОВАНИЕ
Пример 4.
1. Составить список элементов множеств, заданных характеристическими свойствами: 1) А= {x : x2 – 8 x +15=0 };( X 1=3, X 2=5)
2) А = { x : x∈N, –11<x≤–3}. (???) A =0 (нулевое множество?)
2. Доказать, что если А= {x : x2 – 7 x +6=0 } и В={1, 6}, то А=В.
3. Описать множества точек М плоск., таких, что: 1) {М: │ОМ │= R}; (???)
2) {М: │ОМ │≤ R}; 3) {М: │АМ │= │ВМ │}, где А и В — заданные точки.
4. Какая разница в записях А⊂В и А∈В? (первое про подмножество принадлежащее множеству, а второе про элемент принадлежащий множеству?)
5. Доказать, что {{1, 2}, {2, 3}}≠{1, 2, 3}.
6. Верно ли, что {1, 2}∈ (???){{1, 2, 3}, {1, 3}, 1, 2}? Верно ли, что {1, 2}⊆{{1, 2, 3}, {1, 3}, {1, 2}?
7. Привести примеры таких множеств А, В и С, что: 1) А∈В, В∈С, А 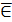 С ; (???)
С ; (???)
2)А⊆В, В⊆С, А⊆С; 3) А∈В, А⊂В.
8. Является ли множество, состоящее из числа 0, пустым?
9. Доказать справедливость соотношения:  ≠ {
≠ {  }.
}.
10. Доказать, что существует только одно множество, не имеющее элементов.
11. Найти все подмножества множеств: 1)  ; 2) {
; 2) {  }; 3) {1, 2}; 4) {a , b , c , d}. (2 ^n )
}; 3) {1, 2}; 4) {a , b , c , d}. (2 ^n )
12. Доказать, что если А⊆В, В⊆А, то А=В, и обратно, если А=В, то А⊆В, В⊆А.
§2. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
Объединением А 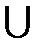 В множеств А и В называется множество, состоящее из элементов, входящих в множества А и В, и только из них, т.е. А
В множеств А и В называется множество, состоящее из элементов, входящих в множества А и В, и только из них, т.е. А 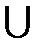 В ={x : x∈A или x∈В}.
В ={x : x∈A или x∈В}.
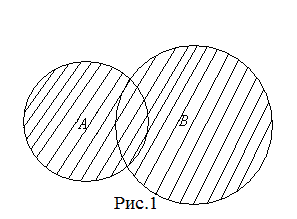 Если один и тот же элемент содержится и во множестве А и во множестве В, то в их объединение он входит только один раз. Схематически объединение множеств А и В изображено на рис.1.
Если один и тот же элемент содержится и во множестве А и во множестве В, то в их объединение он входит только один раз. Схематически объединение множеств А и В изображено на рис.1.
|
|
|
Объединением 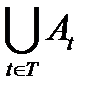 множеств At (t∈T) называется множество, состоящее из элементов, входящих в множества At (t∈T), и только из них (здесь предполагается, что индекс t пробегает все значения из некоторого множества T.
множеств At (t∈T) называется множество, состоящее из элементов, входящих в множества At (t∈T), и только из них (здесь предполагается, что индекс t пробегает все значения из некоторого множества T.
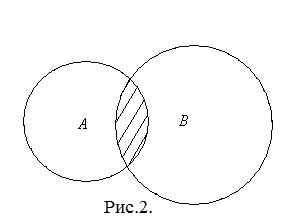
Пересечением А  В множеств А и В называется множество, состоящее из элементов, принадлежащих как множеству А, так и множеству В, и только из них, т.е. А
В множеств А и В называется множество, состоящее из элементов, принадлежащих как множеству А, так и множеству В, и только из них, т.е. А  В={x : x∈A и x∈B}. Схематически пересечение множеств А и В изображено на рис.2.
В={x : x∈A и x∈B}. Схематически пересечение множеств А и В изображено на рис.2.
Пересечением 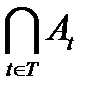 множеств At (t∈T) называется множество, состоящее из элементов, принадлежащих множествам At (t∈T), и только их них.
множеств At (t∈T) называется множество, состоящее из элементов, принадлежащих множествам At (t∈T), и только их них.
Если пересечение множеств не является пустым, то множества называют пересекающимися.
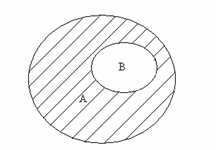 Разностью А∖В множеств А и В называется множество, состоящее из элементов множества А, не входящих в множество В, и только из них, т.е.
Разностью А∖В множеств А и В называется множество, состоящее из элементов множества А, не входящих в множество В, и только из них, т.е.
А∖В={ x : x∈А и x∈???В }. Схематически разность множеств А и В изображена на рис.3.
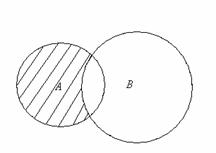
Рис.3.
Разность J∖B, где J — универсальное множество, называется дополнением множества В и обозначается  .
.
Пример 1. Доказать тождество А  А= А
А= А  А=А.
А=А.
|
|
|
Пример 2. Доказать, что если А t⊆B для всех t∈T, то  At⊆В.
At⊆В.
Пример 3. Доказать, что если А⊆В  С, то А
С, то А 
 ⊆С, и обратно.
⊆С, и обратно.
Пример 4. В каком из отношений (X⊂Y, X⊃Y, X=Y) находятся множества X и Y, если: 1) X= А  (В∖С), Y=(А
(В∖С), Y=(А 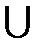 В) ∖ (А
В) ∖ (А 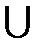 С); ( X ⊃ Y )
С); ( X ⊃ Y )
2) X=(А  В) ∖ С; Y=(А∖С)
В) ∖ С; Y=(А∖С)  (В ∖С); ( x = y )
(В ∖С); ( x = y )
3) X= А ∖ (В 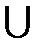 С), Y=(А∖В)
С), Y=(А∖В) 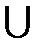 (А∖С). ( x = y )
(А∖С). ( x = y )
Пример 5. Доказать, что: 1) (если)для всех t∈T, В⊆ (знак ⊆, и знак ⊂– абсолютно идентичны???) А t , то В⊆ 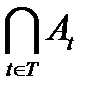 ;
;
2) если для всех t∈T А t⊆В t, то 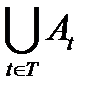 ⊆
⊆ 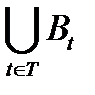 и
и 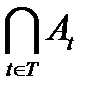 ⊆
⊆ 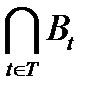 ;
;
3) 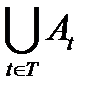 ∖
∖ 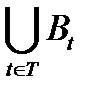 =
=  ∖ В t);
∖ В t);
4) 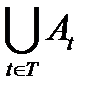 есть наименьшее множество, включающее все множества А t;
есть наименьшее множество, включающее все множества А t;
5) 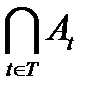 есть наименьшее множество, содержащееся во всех множествах А t.
есть наименьшее множество, содержащееся во всех множествах А t.
(и как всё это доказывать???)
§3. ЭКВИВАЛЕНТНОСТЬ МНОЖЕСТВ
Если каждому элементу множества А по какому-то правилу можно сопоставить один и только один элемент множества В и обратно каждому элементу множества В можно сопоставить один и только один элемент множества А, то говорят, что между множествами А и В установлено взаимно-однозначное взаимодействие.
Множества А и В называются эквивалентными, А ~ В, если между ними можно установить взаимно-однозначное соответствие, в противном случае множества называются неэквивалентными, А  B .
B .
|
|
|
Для установления факта эквивалентности двух множеств достаточно указать какое-либо правило установления их взаимно-однозначного соответствия.
Отношение эквивалентности между множествами обладает свойствами:
1) рефлексивности — A ~ A;
2) симметричности — если A ~ B, то B ~ A;
3) транзитивности — если A ~ B, а В ~ С, то A ~ С.
Мощностью множества А называется класс всех множеств, эквивалентных множеству А, т.е. мощность есть то общее, чем характеризуются все эквивалентные между собой множества.
Если А 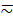 B и А ~ B 1 ⊂B, то мощность множества А считается меньшей мощности множества В.
B и А ~ B 1 ⊂B, то мощность множества А считается меньшей мощности множества В.
Непустое множество А называется конечным, если существует такое число
n∈N, что А ~ {1, 2, …, n}. В этом случае говорят, что множество А имеет мощность, равную n, или что оно имеет n элементов.
Пустое множество также считается конечным, и его мощность равна нулю.
Множество, не являющееся конечным, называется бесконечным.
Множество А, эквивалентное множеству N натуральных чисел, называется счетным, и его мощность обозначается символом  . Для установления счетности множества достаточно указать правило пересчета его элементов всеми натуральными числами.
. Для установления счетности множества достаточно указать правило пересчета его элементов всеми натуральными числами.
|
|
|
Множество, эквивалентное множеству R вещественных чисел, называется множеством мощности континуума, и его мощность обозначается символом с.
Мощности произвольных множеств называются кардинальными числами. Мощности конечных множеств выражаются натуральными числами (или нулем для пустого множества), т.е. кардинальные числа для конечных множеств — натуральные числа (или нуль для пустого множества).
Над мощностями (кардинальными числами) выполнимы только две операции — сложение и умножение. Суммой 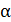 +β двух мощностей α и β множеств А и В, не имеющих общих элементов, называется мощность множества С, являющегося объединением множеств А и В. Произведением αβ двух мощностей α и β множества А и В называется мощность множества С, элементами которого являются все упорядоченные пары, составленные из элементов множеств А и В.
+β двух мощностей α и β множеств А и В, не имеющих общих элементов, называется мощность множества С, являющегося объединением множеств А и В. Произведением αβ двух мощностей α и β множества А и В называется мощность множества С, элементами которого являются все упорядоченные пары, составленные из элементов множеств А и В.
Действия над мощностями:
1) коммутативны — α+β=β+α, αβ=βα;
2) ассоциативны — (α+β) + γ= α + (β+ γ), (αβ) γ= α(βγ);
3) дистрибутивны — (α+β) γ= αγ +βγ.
Пример 1. Можно ли сказать, что если A = B, то A ~ B ?(ДА – по свойству рефлексивности)
Пример2. Установить взаимно-однозначное соответствие между множествами А = { x : x∈R, 0 ≤ x <1} и В = { y : y∈R, a ≤ y <b}.
Пример 3. Доказать равномощность: 1) множества точек окружности и множества точек контура квадрата; 2) множества точек окружности без одной точки и множества точек прямой; 3) множества точек сферы без одной точки и множества точек плоскости.
Пример 4. Доказать, что для любого бесконечного множества А можно выделить его собственное подмножество А1 такое, что А1 ~ A.
Пример 5. Доказать, что: 1) конечное множество не эквиваленто никакому своему собственному подмножеству; 2) два конечных множества эквивалентны тогда и только тогда, когда они содержат одинаковое количество элементов.
Пример 6. Доказать, что: 1) всякое подмножество конечного множества конечно; 2) объединение конечного числа конечных множеств конечно.
Пример 7. Доказать, что не существует множества, содержащего все множества. (В каком смысле? Если учитывать множество элементов списка продуктов в магазине, то конечно- да, а так, почему бы не С)
Пример 8. Доказать, что из всякого бесконечного множества можно выделить счетное подмножество.
Пример 9. Доказать, что среди всех бесконечных множеств счетные множества имеют наименьшую мощность.
Пример 10. Доказать, что всякое подмножество счетного множества счетно или конечно.
Пример 11. Доказать, что множество нечетных чисел счетное.(2n+1)
Пример 12. Доказать, что множество целых неотрицательных чисел счетное.
Пример 13. Доказать, что множество целых чисел, делящихся на 10, счетное.
Пример 14. Доказать, что множество рациональных чисел счетное. (???)
Пример 15.Доказать, что множество точек плоскости с целыми координатами счетное.
Пример 16. Доказать, что если из множества мощности континуума удалить конечное число или счетное подмножество, то оставшееся множество будет множеством мощности континуума.
Пример 17. Определить мощность множества иррациональных чисел.
Пример 18. Доказать, что кардинальных чисел бесконечно много и среди них нет наибольшего.
Пример 19. Доказать, что 2+2=4, 2∙2=4.
§4. ПОНЯТИЕ ФУНКЦИИ.
1.Области определения и значений. График функции. Сложная и обратная функции.
Если даны числовые множества X ={x} и Y={y} и по некоторому закону f каждому элементу x∈X поставлен в соответствие один и только один элемент
y∈Y , то говорят, что на множестве X задана функция y = f ( x ), x называют аргументом функции, y — ее значением.
Через f ( a ) или y ( a ) обозначается то значение y, которое соответствует значению x = a.
Множество X называется областью определения, или областью существования функции, множество Y — областью изменения функции, или областью ее значений.
Для лучшего понимания определения функции следует познакомиться с элементами входящие в это определение.
Df . Величина «у» называется функцией переменной величины «х» если каждому значению переменной х из указанной её области изменения D ( f ) соответствует одно или несколько определенных значений «у».
Записывают это так: 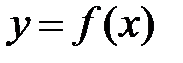 х – аргумент (независимая переменная). Если каждому значению «х» соответствует одно определенное значение у, то функцию «у» называют однозначной.
х – аргумент (независимая переменная). Если каждому значению «х» соответствует одно определенное значение у, то функцию «у» называют однозначной.
Если аргумент «х» может принимать только значения действительных чисел, то функция у называется функцией действительной переменной х.
Если же каждому значению «х» соответствует несколько определенных значений у (два, три и т.д.) то функция «у» называется многозначной (двузначной, трехзначной и т.д.)
Буква 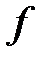 , входящая в равенство
, входящая в равенство 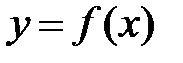 в отличии от букв «
в отличии от букв « 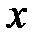 » и «
» и « 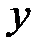 » обозначает не переменную величину, а то правило (закон), по которому устанавливается соответствие между «
» обозначает не переменную величину, а то правило (закон), по которому устанавливается соответствие между « 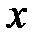 » и «
» и « 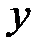 » .
» .
В частности, буква 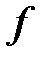 может обозначать совокупность математических операций, которые нужно произвести над аргументом «
может обозначать совокупность математических операций, которые нужно произвести над аргументом « 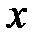 » чтобы получить соответствующее значение «
» чтобы получить соответствующее значение « 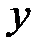 », и указывать последовательность их выполнения.
», и указывать последовательность их выполнения.
Символ 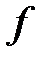 называют характеристикой функции.
называют характеристикой функции.
Буква 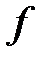 может обозначать не только математические операции и последовательность их выполнения, а и правило сформулированное любым способом (словами, таблицей, графиком и т.д.) по которому каждому значению «
может обозначать не только математические операции и последовательность их выполнения, а и правило сформулированное любым способом (словами, таблицей, графиком и т.д.) по которому каждому значению « 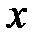 » можно найти соответствующее значение «
» можно найти соответствующее значение « 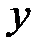 ».
».
Если функция 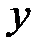 задана формулой
задана формулой 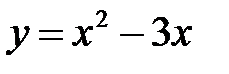 , то роль
, то роль 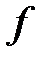 здесь играет предложение:
здесь играет предложение:
«Чтобы получить значение 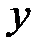 , зная значения х нужно из квадрата числа
, зная значения х нужно из квадрата числа 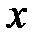 вычесть утроенное это число».
вычесть утроенное это число».
Если функция y = f ( x ) задана аналитически (при помощи формулы), то под областью Х ее определения понимается множество тех вещественных значений аргумента x, при которых аналитическое выражение f ( x ) имеет смысл, т.е. выполнимы все действия, указанные в задании функции. Нахождение области определения функции, как правило, сводится к решению некоторой системы неравенств, содержащих аргумент x. Нахождение области Y значений функции производится либо преобразованием данного аналитического выражения к виду, содержащему функции, области изменения которых известны, либо к нахождению области определения функции, обратной данной.
Функция, заданная разными формулами для различных значений аргумента, называется кусочно-аналитической. Например, 
 — кусочно-аналитическое задание функции (эта функция может быть задана и одной формулой y = x +│ x │). Функция знака числа x , y = sign x, задается так:
— кусочно-аналитическое задание функции (эта функция может быть задана и одной формулой y = x +│ x │). Функция знака числа x , y = sign x, задается так:
y = 

ее график изображен на рис.1.
Если задано уравнение F (x , y)=0, связывающее функцию y и аргумент x, то говорят, что функция y задана неявно. Например, уравнение 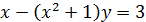
является неявным заданием функции y. Если разрешить это уравнение относительно y, то получим 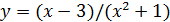 — явное аналитическое задание функции y.
— явное аналитическое задание функции y.
З а м е ч а н и е. Обычно выражение y через x при неявном задании функции не так просто, как в приведенном примере. Но при решении многих задач и не требуется выражать функцию явно.
| Рис.1 |
Пусть функция z = φ(y) определена на множестве Y — множество значений некой функции y = f ( x ) с областью определения X; тогда переменная z является функцией от x на множестве X : z = φ(f(x)).
Функция z = φ(f(x)), аргументом которой является другая функция (точнее, функция другого аргумента), называется сложной функцией переменной x; функция y = f ( x ) называется внутренней, а функция z = φ(y) — внешней. Говорят также, что сложная функция является суперпозицией этих функций или что задана композиция двух функций.
Например, функции 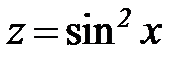 ,
,  являются сложными функциями. Функция
являются сложными функциями. Функция 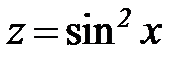 может быть представлена как
может быть представлена как 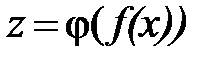 , где
, где  — внутренняя функция, а
— внутренняя функция, а  — внешняя. Пример сложной функции
— внешняя. Пример сложной функции  демонстрирует «трехступенчатую» функциональную зависимость функции z от аргумента x: z=g(φ(f(x))), где t = f(x) =cos x — тригонометрическая функция; y=φ(t) = lg t — логарифмическая функция; z=g(y) =
демонстрирует «трехступенчатую» функциональную зависимость функции z от аргумента x: z=g(φ(f(x))), где t = f(x) =cos x — тригонометрическая функция; y=φ(t) = lg t — логарифмическая функция; z=g(y) = 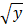 — степенная функция.
— степенная функция.
Функция y = f(x) с областью определения X и множеством значений Y называется взаимно-однозначной, если для любых х1 и х2 из области ее определения Х из неравенства х1≠х2 следует, что f(x 1) ≠ f(x 2), т.е. различным значениям аргумента соответствуют различные значения функции.
Примером взаимно-однозначных функций являются строго монотонные функции. Для функций, не являющихся взаимно-однозначными на всей области определения, часто удается выделить промежутки, на которых они взаимно-однозначны. Например, функция y=x 2 не являются взаимно-однозначной для всех x (для x≠0 различным значениям аргумента x и –x соответствуют равные значения функции y=x 2), но на промежутках (–∞; 0] и [0; +∞) она взаимно-однозначна.
Функция, определенная на множестве Y (множестве значений взаимно-однозначной функции y = f(x)), ставящая в соответствие каждому y∈Y то значение x∈X (из области определения функции y = f(x)), для которого y = f(x), называется обратной к функции y = f(x).
Для нахождения функции (если она существует), обратной данной y = f(x), необходимо выразить x через y : x = φ(y), а затем записать полученную функцию в обычном виде : y = f(x). Например, обратной для функции y =2х+4 является функция y =  х–2.
х–2.
Условия существования обратной функции приведены в § 2 главы III.
Область определения обратной функции совпадает с множеством значений исходной функции, и наоборот, множество значений обратной функции совпадает с областью определения исходной функции.
Графики прямой и обратной функций симметричны относительно прямой y = x.
Суперпозиция взаимно-обратных функций y = f(x) и x = f -1(y) является тождественной функцией: f(f -1(y)) = y; f(f -1(x)) = x .
Пример 1. 1) Выразить объем цилиндра, вписанного в шар радиусом R, как функцию его высоты h.
2) Имеются два куска сплава меди с серебром. В первом куске содержится p % меди, во втором — q % меди (p < q).
| Задание функции | Способ построения ее графика | График | ||||||||||||||||||
| 1. y = f(x)+A |
Параллельный перенос (сдвиг) графика функции y=f(x) вдоль оси OY на |A| единиц вверх, если А>0, или вниз, если A<0. (рис.2.) | |||||||||||||||||||
| 2. y = f(x+a) |
Параллельный перенос графика функции y = f(x) вдоль оси OX на |a| единиц влево, если a>0, или вправо, если a<0. (рис.3.)
| |||||||||||||||||||
| 3. y=kf(x) |
  
–1<k<0 (рис.6).
| |||||||||||||||||||
| 4. y=|f(x)| |
| |||||||||||||||||||
| 5. y=f (kx) |
Сжатие графика функции y=f(x) вдоль оси OX в k раз, если k>1, растяжение вдоль оси OX в 1/k раз, если 0<k<1 (рис.8), симметричное отображение относительно оси OY, если k= –1.(рис.9)
| |||||||||||||||||||
| 6. y=f (|x|) |
 Отбросить часть графика y=f(x), лежащую в левой полуплоскости; остальную часть графика (лежащую в правой полуплоскости) сохранить и, кроме того, отобразить относительно оси OY (рис.10). Отбросить часть графика y=f(x), лежащую в левой полуплоскости; остальную часть графика (лежащую в правой полуплоскости) сохранить и, кроме того, отобразить относительно оси OY (рис.10).
| |||||||||||||||||||
При переплавке х кг первого сплава с у кг второго получили сплав, содержащий r % меди. Выразить зависимость у от х.
2.Четные и нечетные функции.
Функция y = f(x)называется четной , если для всех х из области ее определения выполняется равенство f( – x)= f(x).
Функция y = f(x) называется нечетной, если для всех х из области ее определения выполняется равенство f( – x)= – f(x).
Функции, не четные и не нечетные, называются функциями общего вида.
Свойства четных и нечетных функций.
1. Область определения четной и нечетной функций симметрична относительно начала координат.
2. График четной функции симметричен относительно оси координат.
3. График нечетной функции симметричен относительно начала координат.
4. Сумма, разность, произведение и частное двух четных функций с одной и той же областью определения (знаменатель дроби при этом должен быть отличен от нуля) также являются четными функциями.
5. Сумма и разность двух нечетных функций (с одной областью определения) есть нечетные функции.
6. Произведение и частное двух нечетных функций являются четными функциями.
7. Произведение и частное четной и нечетной функций есть нечетные функции.
При построении графиков четных и нечетных функций достаточно построить только ту часть графика, которая лежит в правой полуплоскости (при х≥0), а затем отобразить ее симметрично относительно оси ординат (для четной функции) или относительно начала координат (для нечетной функции).
Пример 2. Установить, какие из следующих функций являются четными, нечетными и какие — функциями общего вида.
1) y = 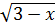 , 2) y =x2 + |x|, 3) y =tg2x – cos x, 4) y = lg
, 2) y =x2 + |x|, 3) y =tg2x – cos x, 4) y = lg  , 5) y = x
, 5) y = x 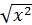 ,
,
6) y = 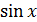 +
+ 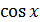 , 7) y =
, 7) y =  , 8) y = (2x –1)/( 2x +1), 9) доказать свойство 5.
, 8) y = (2x –1)/( 2x +1), 9) доказать свойство 5.
Решение 4): Область определения функции y = lg  , симметрична относительно начала координат: x∈(–1,1).При этом f (–x)= lg
, симметрична относительно начала координат: x∈(–1,1).При этом f (–x)= lg  =lg
=lg  = – lg
= – lg  = – f (x), следовательно, функция нечетная.
= – f (x), следовательно, функция нечетная.

3. Периодические функции.
Функция y = f(x) называется периодической, если существует такое число Т>0 (не зависящее от х), что:
1) х+Т и х–Т также входят в область определения функции f(x);
2) для всех х из области определения функции выполняется равенство: f(x +Т)= f(x);
3) среди всех Т есть наименьшее.
Это наименьшее число Т называется периодом функции.
Свойства периодических функций.
1. Область определения периодической функции симметрична относительно начала координат.
2. Для периодической функции y = f(x) справедливо равенство f(x + k Т) = f(x), где Т — период функции, k∈Z; в частности, f(x–Т) = f(x).
3. Если функция y = f(x) периодическая с периодом Т, то функция y = f(ax) также периодическая с периодом Т/| a | (при a ≠0).
4. Если функция y = f(x) периодическая с периодом Т, то функция y = f(x + a) также периодическая с периодом Т.
При построении графика периодической функции достаточно построить часть графика на интервале, равном одному периоду, а затем продолжить его на всю область определения функции.
Пример 3. Исследовать на периодичность следующие функции:
1) y=x2+x–1; 2) y=2; 3)y=sin  x+1; 4) y=sin x – cos x; 5)y=sin 2x – 2tg
x+1; 4) y=sin x – cos x; 5)y=sin 2x – 2tg  ; 6)y=cos2x; 7)y=x–|x|.
; 6)y=cos2x; 7)y=x–|x|.
4. Возрастающие, убывающие и ограниченные функции.
Функция y = f(x), определенная на множестве Х, называется возрастающей, если для любых х1, х2 множества Х из неравенства х1 <х2 следует, что:
f ( x 1 )< f ( x 2 ) (1)
т.е. функция y = f(x) называется возрастающей, если большему значению ее
| Y |
| 0 |
| x2 |
| x1 |
| X |
| f(x1) |
| f(x2) |
аргумента из области определения соответствует большее значение функции (рис.11)
| 0 |
| Y |
| X |
| x2 |
| x1 |
| f(x2) |
| f(x1) |
Рис.11 Рис. 12
Функция y = f(x), определенная на множестве Х, называется убывающей, если для любых х1, х2 множества Х из неравенства х1 <х2 следует, что:
f ( x 1 )< f ( x 2 ), (2)
т.е. функция y = f(x) называется возрастающей, если большему значению ее аргумента из области определения соответствует меньшее значение функции (рис. 12).
Возрастающие и убывающие функции называются строго монотонными.
Если в определении возрастающей функции неравенство (1) заменить на нестрогое f ( x 1 )≤ f ( x 2 ), то такая функция называется неубывающей ( рис.13). Если в определении убывающей функции неравенство (2) заменить на нестрогое f ( x 1 )≥ f ( x 2 ) , то такая функция называется невозрастающей (рис. 14).
Возрастающие, убывающие, невозрастающие, неубывающие функции называются монотонными функциями.
| 0 |
| X |
| Y |
| 0 |
| X |
| Y |
Рис.13 Рис.14
Свойства монотонных функций:
1. Сумма двух возрастающих (убывающих) функций есть функция возрастающая (убывающая).
2. Если функция y = f(x) возрастающая (убывающая), то функция y = –f(x) убывающая (возрастающая).
3. Если функция y = f(x) возрастающая (убывающая), то функция y = 1 / f(x)
убывающая (возрастающая) (f(x)≠0).
4. Суперпозиция двух монотонно возрастающих (убывающих) функций есть
монотонно возрастающая функция.
5. Суперпозиция двух функций, из которых одна монотонно возрастающая, а
другая монотонно убывающая, является монотонно убывающей функцией.
Функция y = f(x), определенная на множестве Х, называется ограниченной сверху на данном множестве, если существует число М такое, что f(x) ≤ М для любого х∈Х.
Функция y = f(x), определенная на множестве Х, называется ограниченной снизу, если существует число m такое, что f(x) ≥ m для любого х∈Х.
Функция y = f(x), определенная на множестве Х, называется ограниченной на данном множестве, на данном множестве, если существует число N >0такое, что |f(x)| ≤ N для любого х∈Х. Ясно, что функция y = f(x) является ограниченной тогда и только тогда, когда она ограничена и сверху, и снизу.
Сумма и произведение ограниченных функций являются также ограниченными функциями.
Пример 4. Исследовать на монотонность следующие функции:
1) y = sin x на отрезке [–π/2, π/2 ]; 2) y = arctg (x 2–2x +3);
2) y = (x 2 +4x +6) ln (x 2 +4x +6); 4) y = (1–x 2)/x; 5) доказать свойство 1 для монотонно убывающих функций
5. Функция натурального аргумента (числовая последовательность).
Частным случаем функции является функция натурального аргумента y = f(n), (n∈N), которая обычно обозначается xn и называется числовой последовательностью. Областью определения такой функции является множество N натуральных чисел, а каждое значение xn называется членом последовательности. Значению аргумента n соответствует число xn , стоящее на месте с номером n в этой последовательности. Последовательность считается заданной, если указано правило, по которому каждому значению аргумента n (натуральному числу) поставлено в соответствие единственное значение xn. Число xn называется общим членом последовательности. Для задания последовательности достаточно знать ее общий член, ибо, зная номер члена последовательности, всегда можно найти и сам член. Так, если xn= 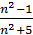 — общий член последовательности, то ее первые члены равны 0, 3/9, 8/14, …, а, например, десятый член x 10=99/105.
— общий член последовательности, то ее первые члены равны 0, 3/9, 8/14, …, а, например, десятый член x 10=99/105.
Если существует число m (М) такое, что для всех (n∈N) справедливо неравенство xn ≥m (xn ≤ M).
Последовательность xn называется ограниченной, если существует число L такое, что справедливо неравенство |xn| ≤ L.
Последнее определение равносильно тому, что последовательность xn ограничена и снизу и сверху.
Последовательность xn называется возрастающей (неубывающей), если для всех (n∈N) справедливо неравенство xn +1 ≥ xn, и убывающей (невозрастающей), если для всех (n∈N) справедливо неравенство xn +1 ≤ xn. Если верны соответственно строгие неравенства xn +1 > xn или xn +1 < xn, то последовательности называются строго возрастающей или строго убывающей.
Пример 5. 1) Найти формулу общего члена последовательности xn , если x 1=1, а xn= xn -1 + d.
3) Доказать, что последовательность xn= 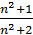 ограничена.
ограничена.
4) Доказать, что последовательность xn = lg n – lg (n – 1) монотонна, начиная с некоторого номера n ( n >1).
5) Найти наибольший член последовательности xn = n 2 /2n.
6) Найти наибольший член последовательности xn = n 2 – 5n +1.
7) Доказать, что последовательность xn = 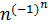 не ограничена.
не ограничена.
8) Найти области определения функций:
1. y = 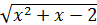 ; 2. y = 1/(
; 2. y = 1/( 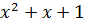 ); 3. y =
); 3. y =  ;
;
4. y =  ; 5. y =
; 5. y =  ; 6. y =
; 6. y = 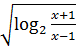 ;
;
7. y = 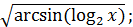 8. y =
8. y =  +
+  ; 9. y =tg
; 9. y =tg  ;
;
10. y =  .
.
9) Найти множество значений функций:
1) y =sin2x – cos2x; 2) y = 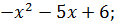 3) y =
3) y =  ;
;
4) y = 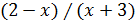 ; 5)
; 5) 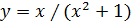 ; 6)
; 6) 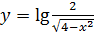 ;
;
7) 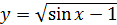 ; 8)
; 8) 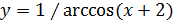 .
.
10) Построить графики функций:
1) 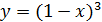 ; 2)
; 2)  ; 3)
; 3) 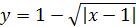 ; 4)
; 4) 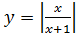 ;
;
5) 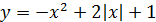 ; 6)
; 6) 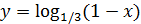 ; 7)
; 7) 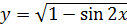 ;
;
8) 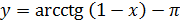 ; 9)
; 9)  ; 10)
; 10) 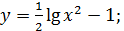
11)  1/3)|x|; 12)
1/3)|x|; 12)  ; 13)
; 13)  x/2)
x/2) 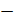 cos(x/2))2;
cos(x/2))2;
14) 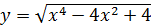 ; 15)
; 15)  .
.
11) Найти суперпозиции функций 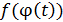 :
:
1)  ,
, 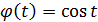 ; 2)
; 2) 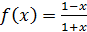 ,
,  ;
;
3) 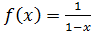 ,
, 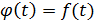 ; 4)
; 4) 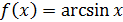 ,
,  ;
;
5) 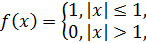
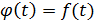 ;
;
6) 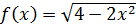 ,
, 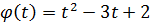 .
.
12) Найти функции, обратные данным:
1) 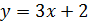 ; 2)
; 2)  ; 3)
; 3) 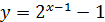 ; 4)
; 4) 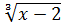 ;
;
5)  ; 6)
; 6) 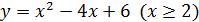 .
.
13) Установить, какие из следующих функций являются четными, нечетными и функциями общего вида:
1) 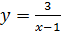 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ;
;
5) 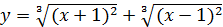 ; 6)
; 6) 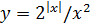 ; 7)
; 7) 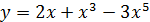 ;
;
8) 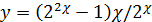 ;
;
9) доказать свойства 4) –7) четных и нечетных функций;
10) доказать, что любую функцию с областью определения, симметричной относительно начала координат, можно представить в виде суммы четной и нечетной функций.
14) Исследовать на периодичность следующие функции:
1)  ; 2)
; 2)  ; 3)
; 3) 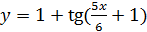 ;
;
4)  ; 5)
; 5) 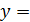 sin4 x – sin4 x; 6)
sin4 x – sin4 x; 6)  ;
;
7) 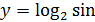 2 x; 8)
2 x; 8) 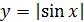 .
.
15) Исследовать на монотонность следующие функции:
1)  2)
2) 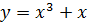 ; 3)
; 3) 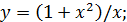
4)  ; 5)
; 5)  ; 6)
; 6) 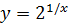 .
.
16) Установить, являются ли ограниченными следующие функции:
1)  ; 2)
; 2) 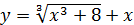 ;
;
3) 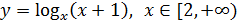 ; 4)
; 4) 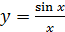 ;
;
5) 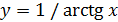 ; 6)
; 6)  .
.
17) Доказать, что последовательность ограничена:
1) 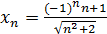 ; 2)
; 2)  ; 3)
; 3) 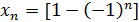 .
.
18) Найти наибольший член последовательности:
1) 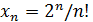 2)
2)  ; 3)
; 3) 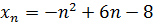 .
.
19) Найти формулу общего члена последовательности 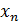 :
:
 ,
, 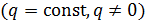 .
.
20) Найти наименьший член последовательности:
1) 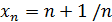 ; 2)
; 2) 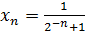 ; 3)
; 3) 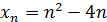 .
.
21) Доказать, что последовательность не является ограниченной:
1)  ; 2)
; 2) 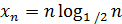 ; 3)
; 3)  .
.
22) Доказать, что последовательность монотонна:
1) 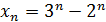 ; 2)
; 2)  ; 3)
; 3) 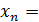
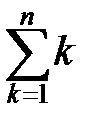 .
.
ГЛАВА II
ПРЕДЕЛ
§1 ПОНЯТИЕ ПРЕДЕЛА ФУНКЦИИ
1.Предел функции.
Число А называется пределом функции f(x) при х, стремящемся к a , если функция f(x) определена в некоторой окрестности точки х= a , исключая, может быть, саму эту точку, и для любого числа ε >0 существует такое число 𝛿(ε)>0, что для всех х ≠ a , таких, что | х– a | <𝛿, выполняется неравенство | f(x) – A | <ε.
Иными словами, число А называется пределом функции f(x) при х→ a , если для произвольной ε-окрестности точки у=А существует 𝛿-окрестность точки х= a , для всех точек которой (кроме, может быть, точки х= a) значения функции f(x) попадают в ε-окрестность точки А.
| A |
| A–ε |
| A+ε |
| a |
| a+δ |
| a–δ |
| Y |
| 0 |
| X |
| Рис.1 |

:
для x∈(a – 𝛿, a +𝛿) график размещается внутри полосы, ограниченной прямыми y = A ± ε.
Следует иметь в виду, что существует бесконечное множество значений 𝛿, отвечающих заданному ε, среди которых есть наибольшее. Однако если речь идет о проверке равенства
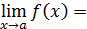 A , то достаточно найти одно значение 𝛿(или доказать его существование), соответствующее произвольному ε>0, заменив неравенство | f(x)– A | <ε более простым, к нему приводящим. При этом часто бывает удобной замена переменной x – a
A , то достаточно найти одно значение 𝛿(или доказать его существование), соответствующее произвольному ε>0, заменив неравенство | f(x)– A | <ε более простым, к нему приводящим. При этом часто бывает удобной замена переменной x – a  t .
t .
Пример 1. Доказать, пользуясь определением предела функции, что 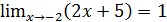 . Каким должно быть число 𝛿>0, чтобы для x∈(–2– 𝛿, –2+𝛿) значения функции 2x +5 отличались от 1 меньше, чем на 0,1; 0,01; 0,001?
. Каким должно быть число 𝛿>0, чтобы для x∈(–2– 𝛿, –2+𝛿) значения функции 2x +5 отличались от 1 меньше, чем на 0,1; 0,01; 0,001?
Решение: Рассмотрим произвольное число ε >0. Надо убедиться в существовании такого числа 𝛿(ε)>0, чтобы из неравенства |x+2| <𝛿, x ≠ –2, следовало неравенство 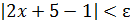 , т.е
, т.е 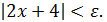 Последнее неравенство равносильно следующему:
Последнее неравенство равносильно следующему: 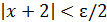 , так что можно взять 𝛿(ε)= ε/2 или любое положительное число меньше его. Значит,
, так что можно взять 𝛿(ε)= ε/2 или любое положительное число меньше его. Значит, 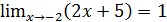 , ибо для любого числа ε >0 найдено 𝛿= ε/2 такое, что для всех x ≠ –2 и удовлетворяющих неравенству
, ибо для любого числа ε >0 найдено 𝛿= ε/2 такое, что для всех x ≠ –2 и удовлетворяющих неравенству 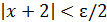 ,выполняется неравенство
,выполняется неравенство 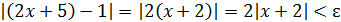 .
.
Полагая в формуле 𝛿(ε)= ε/2 ε=0,1; ε=0,01; ε=0,001, находим 𝛿(0,1)=0,05; 𝛿(0,01)=0,005; 𝛿(0,001)=0,0005.
Пример 2. Доказать, исходя из определения предела функции, что

Решение. Возьмем произвольное число ε >0 и выясним, существует ли такое число 𝛿>0, что из неравенства  , x≠1, следует неравенство
, x≠1, следует неравенство  . Если положить х–1=t, то доказательство сводится к решению вопроса: найдется ли такое число 𝛿>0, чтобы из неравенства
. Если положить х–1=t, то доказательство сводится к решению вопроса: найдется ли такое число 𝛿>0, чтобы из неравенства  вытекало, что
вытекало, что  ?
?
С этого момента рассуждения можно вести по-разному. Используя известное неравенство  , получим
, получим 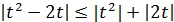 и потребуем, чтобы каждое слагаемое, стоящее в правой части, было меньше ε/2:
и потребуем, чтобы каждое слагаемое, стоящее в правой части, было меньше ε/2: 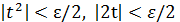 . Полученная система неравенств равносильна следующей:
. Полученная система неравенств равносильна следующей: 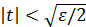 ,
, 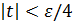 , и за 𝛿 можно взять любое число меньше
, и за 𝛿 можно взять любое число меньше 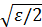 и
и  , например
, например 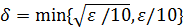 .
.
Или иначе, поскольку  , то при
, то при 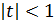 ,
, 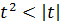 и
и  . Отсюда ясно, что если
. Отсюда ясно, что если  , т.е.
, т.е. 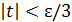 , то тем более
, то тем более  . Последнее неравенство есть результат одновременного выполнения условий
. Последнее неравенство есть результат одновременного выполнения условий 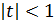 и
и 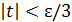 . Поэтому, взяв
. Поэтому, взяв 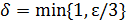 , для
, для  , т.е. для
, т.е. для  , будем иметь одновременно и
, будем иметь одновременно и 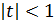 , и
, и  , из чего следует, что
, из чего следует, что  , т.е.
, т.е.  . Значит,
. Значит,

Пример 3. Проверить равенство
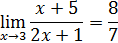
Решение. Задавшись некоторым числом ε >0, составим неравенство 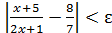 . Элементарными преобразованиями он приводится к равносильному
. Элементарными преобразованиями он приводится к равносильному 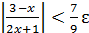 . Если неравенство верно, то существует 𝛿>0 такое, что множество значений x, определяемых условием
. Если неравенство верно, то существует 𝛿>0 такое, что множество значений x, определяемых условием 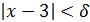 , удовлетворяет этому неравенству. Сделав замену переменной
, удовлетворяет этому неравенству. Сделав замену переменной 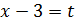 , получим два неравенства:
, получим два неравенства:  и
и  , из которых первое должно быть следствием второго. Пусть
, из которых первое должно быть следствием второго. Пусть 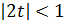 , т.е.
, т.е. 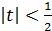 , тогда
, тогда  и
и  . Поэтому если
. Поэтому если  , то тем более
, то тем более  . Приняв
. Приняв 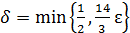 , нетрудно проверить, что для любого ε >0 найдено 𝛿>0 зависящее от ε, а именно
, нетрудно проверить, что для любого ε >0 найдено 𝛿>0 зависящее от ε, а именно 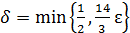 такое, что для любых x ≠ 3 из области определения функции, удовлетворяющих неравенству
такое, что для любых x ≠ 3 из области определения функции, удовлетворяющих неравенству 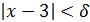 , выполняется неравенство
, выполняется неравенство 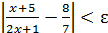 , следовательно,
, следовательно,
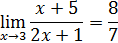
Пример 4. Доказать, что
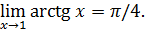
Решение. Возьмем некоторое число ε >0. Чтобы убедиться в справедливости равенства, достаточно найти такое число 𝛿>0, для которого неравенство  приводит к неравенству
приводит к неравенству  < ε. Это неравенство верно при любом х, если
< ε. Это неравенство верно при любом х, если 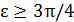 (ибо
(ибо  ). Для таких значений ε в качестве 𝛿 можно взять любое положительное число. Чтобы найти 𝛿 при ε
). Для таких значений ε в качестве 𝛿 можно взять любое положительное число. Чтобы найти 𝛿 при ε 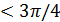 , заметим, что условие
, заметим, что условие  < ε равносильно такому
< ε равносильно такому  , т.е.
, т.е.  . Если ε
. Если ε 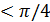 , то
, то 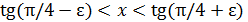 и
и 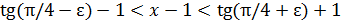 .
.
Если же 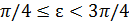 , то двойное неравенство можно заменить одним, а именно неравенством
, то двойное неравенство можно заменить одним, а именно неравенством 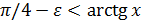 (ибо
(ибо 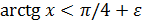 при всех х) или неравенством
при всех х) или неравенством  . В этом последнем случае, очевидно, можно взять
. В этом последнем случае, очевидно, можно взять  . При ε
. При ε 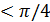 из двух чисел
из двух чисел 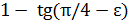 и
и 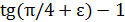 первое будет меньше (это видно из формул
первое будет меньше (это видно из формул 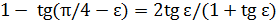 ;
; 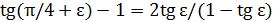 ), так что для 𝛿 можно принять то же выражение. Учитывая, что при
), так что для 𝛿 можно принять то же выражение. Учитывая, что при 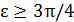 в качестве 𝛿 можно взять любое положительное число, получаем окончательно
в качестве 𝛿 можно взять любое положительное число, получаем окончательно
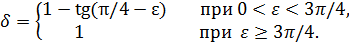
Тогда при таких 𝛿 для любого ε >0 из неравенства  выполняется неравенство
выполняется неравенство  < ε, следовательно,
< ε, следовательно,
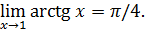
2.Односторонние пределы.
Число А называется левосторонним пределом функции f(x), или пределом слева, в точке х= a, если функция f(x) определена в некоторой левосторонней окрестности точки х= a, исключая, может быть, саму эту точку, и если для любого числа ε >0 существует такое число 𝛿(ε)>0, что из неравенства a – 𝛿< x <a следует неравенство |f(x) – A|< ε.
Для предела слева применяются обозначения  , или f (a –0), так что приведенное определение можно записать, например, в виде равенства
, или f (a –0), так что приведенное определение можно записать, например, в виде равенства  равосторонний предел функции, или предел справа, определяется аналогично и обозначается
равосторонний предел функции, или предел справа, определяется аналогично и обозначается
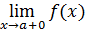 или f (a +0).
или f (a +0).
При a =0 применяются обозначения 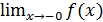 , или f (–0) для предела слева и
, или f (–0) для предела слева и  , или f (+0) для предела справа.
, или f (+0) для предела справа.
Формально понятие предела слева(справа) получается из определения предела функции при условии 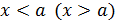 и может быть изложено так: равенство
и может быть изложено так: равенство
 (или f (a –0) =
(или f (a –0) =  ) означает, что произвольной ε-окрестности точки y =
) означает, что произвольной ε-окрестности точки y =  можно поставить в соответствие левостороннюю δ-окрестность точки х= a, для всех точек которой, кроме, может быть, самой точки х= a, значения функции f(x) попадают в ε-окрестность точки
можно поставить в соответствие левостороннюю δ-окрестность точки х= a, для всех точек которой, кроме, может быть, самой точки х= a, значения функции f(x) попадают в ε-окрестность точки  . Аналогичный смысл имеет равенство
. Аналогичный смысл имеет равенство
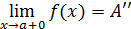
(или f (a +0) = 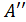 ).
).
Вообще говоря, f (a –0) ≠ f (a +0). Такая ситуация и представлена на рис.2, где (a – δ′, a) есть левосторонняя δ′-окрестность точки х= a, отвечающая ε-окрестности точки y =  , а (a , a +δ″) есть правосторонняя δ″-окрестность точки х= a, соответствующая ε-окрестности точки
, а (a , a +δ″) есть правосторонняя δ″-окрестность точки х= a, соответствующая ε-окрестности точки 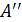 .
.
Условие f (a –0) = f (a +0) является необходимым и достаточным условием существования  . (Тогда
. (Тогда
 = f (a –0) = f (a +0).)
= f (a –0) = f (a +0).)
| Рис.3 |
| Рис.2 |
| a |
| a –δ″ |
| a+δ″ |
| A′′ |
| A′′ – ε |
| A′′ + ε |
| A + ε |
| A′ |
| A′– ε |
| A′+ ε |
| –b |
| b |
| 0 |
| 0 |
| A |
| A – ε |
| Y |
| Y |
| X |
| X |


Пример 5. Доказать, что

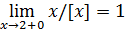 . (Символ [x] означает целую часть от числа x, т.е. наибольшее целое число, не превосходящее x.)
. (Символ [x] означает целую часть от числа x, т.е. наибольшее целое число, не превосходящее x.)
Решение. Для x∈[1,2) [x]=1 и x /[x]=x . При произвольном ε >0 неравенство  можно записать так:
можно записать так: 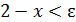 . Следовательно, если принять
. Следовательно, если принять  , то из неравенства
, то из неравенства 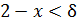 , с одной стороны, следует, что x∈(1,2) (ибо 𝛿>0), а с другой стороны
, с одной стороны, следует, что x∈(1,2) (ибо 𝛿>0), а с другой стороны 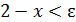 , что формально можно записать и так:
, что формально можно записать и так: 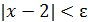 или
или  , следовательно,
, следовательно, 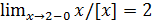 .
.
Чтобы доказать второе равенство, заметим, что для x∈(2,3) неравенство 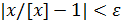 переходит в неравенство
переходит в неравенство 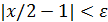 или
или 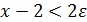 . Поэтому, взяв
. Поэтому, взяв 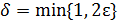 для
для 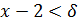 , т.е. для x∈(2,3), получим
, т.е. для x∈(2,3), получим 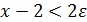 , или
, или 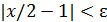 . Поскольку [x]=2, то x /2 = x /[x], и условие
. Поскольку [x]=2, то x /2 = x /[x], и условие 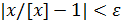 есть следствие неравенства
есть следствие неравенства 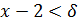 . Значит,
. Значит,  .
.
3.Предел функции в бесконечно удаленной точке.
Понятие предела функции, естественно, обобщается на тот случай, когда a не есть конечное число, если ввести понятие окрестности бесконечно удаленной точки как множества всех значений х, для которых |x| >b, где b >0 — произвольное число. Тогда равенство 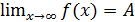 по определению означает, что всякому числу
по определению означает, что всякому числу 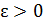 можно поставить в соответствие число b(ε)>0, такое, что при |x|>b выполняется неравенство |f(x)–A|< ε.
можно поставить в соответствие число b(ε)>0, такое, что при |x|>b выполняется неравенство |f(x)–A|< ε.
Число b(ε), зависящее от выбранного ε, играет в этом определении ту же роль, что число 𝛿(ε) в определении предела
 . Каждому значению ε отвечает бесконечное множество значений b , среди которых есть наименьшее, соответствующее наибольшей окрестности бесконечно удаленной точки.
. Каждому значению ε отвечает бесконечное множество значений b , среди которых есть наименьшее, соответствующее наибольшей окрестности бесконечно удаленной точки.
Геометрический смысл записи
 виден на рис.3 произвольной ε-окрестности точки y = A можно сопоставить окрестность бесконечно удаленной точки, т.е. множество x таких, что |x|>b, для всех точек которой A– ε < f(x)< A+ ε, т.е. график функции размещается в полосе, ограниченной прямыми у=А±ε.
виден на рис.3 произвольной ε-окрестности точки y = A можно сопоставить окрестность бесконечно удаленной точки, т.е. множество x таких, что |x|>b, для всех точек которой A– ε < f(x)< A+ ε, т.е. график функции размещается в полосе, ограниченной прямыми у=А±ε.
В частности, если x →+∞ или x → –∞, определение предела функции выглядит следующим образом:
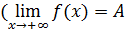 ), если для любого положительного числа ε существует число b , такое, что как только x > b , выполняется неравенство |f(x)–A|< ε (рис.4);
), если для любого положительного числа ε существует число b , такое, что как только x > b , выполняется неравенство |f(x)–A|< ε (рис.4);
число А называется пределом функции f(x) при x → –∞
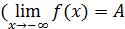 ), если для любого положительного числа ε существует число b , такое, что как только x < b , выполняется неравенство |f(x)–A|< ε (рис.5).
), если для любого положительного числа ε существует число b , такое, что как только x < b , выполняется неравенство |f(x)–A|< ε (рис.5).
Понятия, определяемые равенствами
 ,
,
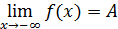 обобщают понятия односторонних пределов функции. Рис.4 и 5 дают их геометрическую интерпретацию.
обобщают понятия односторонних пределов функции. Рис.4 и 5 дают их геометрическую интерпретацию.
Пример 6. Доказать, что
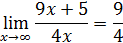 . Каким должно быть число b, чтобы для |x | > b значения функции отличались от 9/4 меньше, чем на 0,1; 0,002; 0,000005?
. Каким должно быть число b, чтобы для |x | > b значения функции отличались от 9/4 меньше, чем на 0,1; 0,002; 0,000005?
Решение. Пусть ε >0 — произвольное число. Доказываемое утверждение верно, если существует b >0 такое, что при |x | > b выполняется неравенство |f(x)–9/4|< ε, т.е. 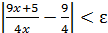 , или
, или  . Последнее неравенство равносильно следующему: |x | >5/(4ε), так что положив b =5/(4ε), при |x | > b получим как следствие
. Последнее неравенство равносильно следующему: |x | >5/(4ε), так что положив b =5/(4ε), при |x | > b получим как следствие  , или
, или 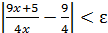 . Следовательно,
. Следовательно, 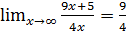 .
.
На остальные вопросы получаем ответ простым вычислением значений b(ε) = =5/(4ε) при ε, равном 0,1, 0,002 и 0,000005, который можно оформить так:
| ε | 0,1 | 0,002 | 0,000005 |
| b | 12,5 | 625 | 250000 |
Пример 7. Доказать, что 

Решение. Исходя из определения предела функции, для любого ε >0 надо найти такое b, что для всех x < b выполняется неравенство 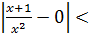 ε.
ε.
Преобразуем последнее неравенство:
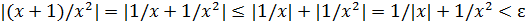 и потребуем, чтобы каждое из слагаемых было меньше ε/2, тогда их сумма будет меньше ε: 1/|x |< ε/2, 1/x 2 < ε/2, или |x |>2/ ε, |x |>
и потребуем, чтобы каждое из слагаемых было меньше ε/2, тогда их сумма будет меньше ε: 1/|x |< ε/2, 1/x 2 < ε/2, или |x |>2/ ε, |x |> 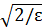 .
.
Так как x → –∞, то можно считать x <0 и тогда |x |= – x, и система неравенств будет равносильной следующей: – x>2/ε, – x > 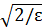 или x<–2/ε, x <–
или x<–2/ε, x <– 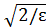 . Вместо b можно взять, например, min{–
. Вместо b можно взять, например, min{– 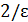 , –
, – 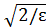 }. Итак, для всех x< min{–
}. Итак, для всех x< min{– 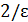 , –
, – 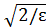 } при любом ε >0 выполняется неравенство
} при любом ε >0 выполняется неравенство 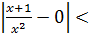 ε, следовательно,
ε, следовательно,  .
.
4.Предел числовой последовательности.
Функция, заданная на множестве натуральных чисел, называется числовой последовательностью.
Говорят, что последовательность {xn} имеет пределом число А ( 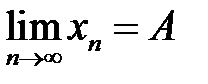 ), если для любого положительного числа ε существует такое число N, что для всех n>N выполняется неравенство | xn –A|< ε.
), если для любого положительного числа ε существует такое число N, что для всех n>N выполняется неравенство | xn –A|< ε.
Последовательность, имеющая конечный предел, называется сходящейся; всякая иная последовательность расходящаяся.
Пример 8. Доказать, что
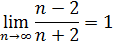 .
.
Решение. По определению предела последовательности надо по любому числу ε >0 найти такое число N, чтобы для любых n>N выполнялось неравенство  .
.
Если преобразовать левую часть неравенства, то  , откуда n >4/
, откуда n >4/ 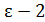 . Если 4/
. Если 4/ 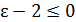 , т.е. при
, т.е. при  , то исходное неравенство будет выполняться для всех натуральных n, а если 4/
, то исходное неравенство будет выполняться для всех натуральных n, а если 4/ 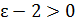 , то в качестве числа N можно рассмотреть число 4/
, то в качестве числа N можно рассмотреть число 4/ 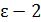 или его целую часть, т.е. N=[4/
или его целую часть, т.е. N=[4/ 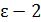 ].
].
Заметим, что здесь важно найти какое-либо число N, не обязательно наименьшее, поэтому можно упростить вычисления для его отыскания. От неравенства 4/(n+2)< ε перейдем к более простому 4/(n+2)<4/n , так как n +2>n. Если N выбрать так, чтобы для n>N выполнялось неравенство 4/n< ε, то тем более для этих n будет выполняться неравенство 4/(n+2)< ε. От неравенства 4/n< ε перейдем к эквивалентному n >4/ ε. За число N можно взять число 4/ε или, например, его целую часть, т.е. N=[4/ε].
Итак, для любого положительного числа ε найдено число N такое, что для всех n, больших его, выполняется неравенство
 .
.
Пример 9. Доказать, что
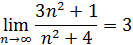
Решение. В соответствии с определением предела последовательности надо по любому числу ε >0 найти такое число N, чтобы для любых n>N выполнялось неравенство  .
.
Преобразуем его левую часть:
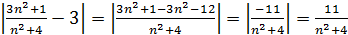 .
.
Заметим, что 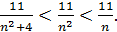 Если число N выбрать так, чтобы для всех n>N выполнялось неравенство 11/n <ε, то тем более для этих n будет выполняться неравенство 11/(n2+4)< ε, начиная с n >11/ε, т.е. за число N можно взять, например, 11/ε или его целую часть [11/ε].
Если число N выбрать так, чтобы для всех n>N выполнялось неравенство 11/n <ε, то тем более для этих n будет выполняться неравенство 11/(n2+4)< ε, начиная с n >11/ε, т.е. за число N можно взять, например, 11/ε или его целую часть [11/ε].
5.Бесконечно малые и бесконечно большие функции.
Функция f(x) называется бесконечно малой при x , стремящемся к a , если
 .
.
Из определения предела функции следует, что для выполнения равенства
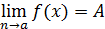 необходимо и достаточно, чтобы разность f(x)–A была бесконечно малой при x → a.
необходимо и достаточно, чтобы разность f(x)–A была бесконечно малой при x → a.
| V |
| V |
| Рис.6 |
| 0 |
| –E |
| E |
| a+δ |
| a–δ a |
| X |
| Y |
 Примерами бесконечно малых являются следующие функции: 2x +4 при x →–2, x 2–4x +3 при x →1, (x +5)/(2x +1)–8/7 при x →3, arctgx–π/4 при x →1, x /[x]–2 при x →2–0, x /[x]–1 при x →2+0, (9x +5)/(4x)–9/4 при x →∞, x+1/x2 при x →–∞, (n+2)/(n–2) – 1 при x →∞ (см. примеры 1–8).
Примерами бесконечно малых являются следующие функции: 2x +4 при x →–2, x 2–4x +3 при x →1, (x +5)/(2x +1)–8/7 при x →3, arctgx–π/4 при x →1, x /[x]–2 при x →2–0, x /[x]–1 при x →2+0, (9x +5)/(4x)–9/4 при x →∞, x+1/x2 при x →–∞, (n+2)/(n–2) – 1 при x →∞ (см. примеры 1–8).
Если f(x) и φ(x) — бесконечно малые при x → a, то их сумма и произведение есть бесконечно малая, кроме того, произведение бесконечно малой на величину ограниченную есть бесконечно малая функция. Функция f(x) называется бесконечно большой при x, стремящемся к a, если 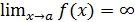 (или ±∞).
(или ±∞).
Иначе говоря, любой окрестности V точки y =∞ (или ±∞) можно поставить в соответствие δ-окрестность точки x = a, для всех точек которой, отличных от a, f(x)∈V . Геометрически это означает, что для x∈(a –δ, a +δ), x≠a , график функции y = f(x) лежит вне полосы, ограниченной прямыми y =± E .
Можно дать определение бесконечно большой иначе.
| Рис.8 |
| Рис.7 |
| a |
| a–δ |
| a–δ a |
| a+δ |
| a+δ |
| E |
| –E |
| 0 |
| 0 |
| Y |
| Y |
| X |
| X |
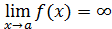 , если для любого числа Е>0 существует число δ(Е)>0, такое, что для всех х, удовлетворяющих неравенству |x – a|<δ и x≠a, выполняется неравенство | f(x)|>E .
, если для любого числа Е>0 существует число δ(Е)>0, такое, что для всех х, удовлетворяющих неравенству |x – a|<δ и x≠a, выполняется неравенство | f(x)|>E .
2)
 , если для любого числа Е>0 существует число δ(Е)>0, такое, что для всех х, удовлетворяющих неравенству |x – a|<δ и x≠a, выполняется неравенство f(x)>E (рис.7).
, если для любого числа Е>0 существует число δ(Е)>0, такое, что для всех х, удовлетворяющих неравенству |x – a|<δ и x≠a, выполняется неравенство f(x)>E (рис.7).
| X |
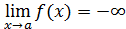 , если для любого числа Е существует число δ(Е)>0, такое, что для всех х, удовлетворяющих неравенству |x – a|<δ и x≠a, выполняется неравенство f(x)<E (рис.8).
, если для любого числа Е существует число δ(Е)>0, такое, что для всех х, удовлетворяющих неравенству |x – a|<δ и x≠a, выполняется неравенство f(x)<E (рис.8).
Понятие бесконечно большой распространяется и на случай, когда a=∞ (a=+∞, a= –∞).
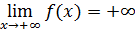 , если для любого числа Е>0 существует число такое b, что для всех х> b выполняется неравенство f(x)>E (рис.9);
, если для любого числа Е>0 существует число такое b, что для всех х> b выполняется неравенство f(x)>E (рис.9);
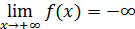 , если для любого числа Е существует число такое b, что для всех х> b выполняется неравенство f(x)<E (рис.10);
, если для любого числа Е существует число такое b, что для всех х> b выполняется неравенство f(x)<E (рис.10);
| X |

|
| 0 |
| E |
| Y |
| Y |
| 0 |
| b |
| X |
| E |
Рис. 9 Рис.10
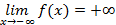 , если для любого числа
, если для любого числа 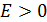 существует такое число
существует такое число 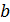 , что для всех
, что для всех 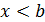 выполняется неравенство
выполняется неравенство  (рис. 11).
(рис. 11).
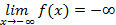 , если для любого числа
, если для любого числа 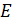 существует такое число
существует такое число 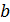 , что для всех
, что для всех 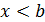 выполняется неравенство
выполняется неравенство  (рис. 12).
(рис. 12).
| b |
| 0 |
| X |
| E |
| Y |
| b |
| E |
| 0 |
| X |
| Y |
Рис. 11 Рис.12
Между бесконечно большими и бесконечно малыми существует простая связь: если  при
при 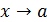 — бесконечно малая, то
— бесконечно малая, то 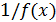 при
при 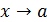 бесконечно большая, и обратно.
бесконечно большая, и обратно.
Пример 10. Доказать, что функция 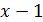 есть бесконечно малая при
есть бесконечно малая при 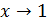 . (Иногда задачи такого типа можно встретить в такой формулировке: доказать, что функция
. (Иногда задачи такого типа можно встретить в такой формулировке: доказать, что функция 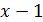 есть бесконечно малая в точке
есть бесконечно малая в точке 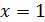 . Здесь подразумевается не значение функции в точке
. Здесь подразумевается не значение функции в точке 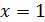 , а её изменения при значениях
, а её изменения при значениях 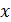 , близких к единице.)
, близких к единице.)
Решение. Согласно определению бесконечно малой достаточно показать, что 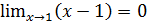 .
.
Зафиксируем число  и покажем существование такого числа
и покажем существование такого числа 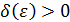 , что неравенство
, что неравенство  или
или  выполняется для всех
выполняется для всех 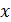 , удовлетворяющих неравенству
, удовлетворяющих неравенству 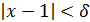 . Очевидно, что из неравенства
. Очевидно, что из неравенства 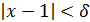 следует, что
следует, что  , значит,
, значит,
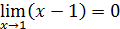 , и функция
, и функция 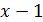 — бесконечно малая при
— бесконечно малая при 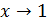 .
.
Пример 11. Доказать, что

Решение. Обозначим
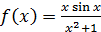 ,
, 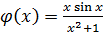 ,
, 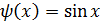 .
.
Тогда 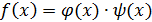 . Заметим, что
. Заметим, что
 , т.е.
, т.е. 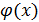 — бесконечно малая при
— бесконечно малая при  (докажите это самостоятельно, используя пример 7), а
(докажите это самостоятельно, используя пример 7), а  — ограниченная функция, так как
— ограниченная функция, так как 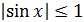 . Тогда
. Тогда
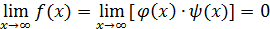 как произведение бесконечно малой на ограниченную функцию.
как произведение бесконечно малой на ограниченную функцию.
Пример 12. Доказать, что функция  бесконечно большая при
бесконечно большая при 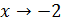 .
.
Решение. Так как при 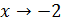 функция
функция  бесконечно малая, то функция
бесконечно малая, то функция  бесконечно большая.
бесконечно большая.
Пример 13. Доказать, что
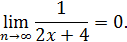
Решение. Так как при  функция
функция  бесконечно большая, то
бесконечно большая, то  бесконечно малая, а тогда
бесконечно малая, а тогда
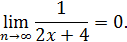
Пример 14. Доказать, что последовательность 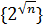 является бесконечно большой при
является бесконечно большой при 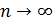 .
.
Решение. Здесь необходимо доказать, что 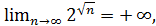 т.е. что
т.е. что 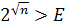 , где
, где 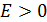 — произвольное число, для всех
— произвольное число, для всех 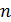 , начиная с некоторого номера
, начиная с некоторого номера 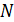 . Используя монотонность логарифмической функции (основание
. Используя монотонность логарифмической функции (основание 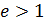 ), получим
), получим  ,
,  ,
,  , и за число
, и за число 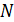 можно взять, например, целую часть числа
можно взять, например, целую часть числа 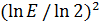 , т.е.
, т.е.
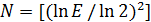 . Итак, для всех
. Итак, для всех  выполняется неравенство
выполняется неравенство 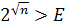 , следовательно, последовательность
, следовательно, последовательность 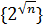 бесконечно большая.
бесконечно большая.
Пример 15. Доказать, что функция 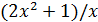 бесконечно большая при
бесконечно большая при  .
.
Решение. Взяв некоторое число 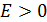 , выясним, существует ли такое
, выясним, существует ли такое  , чтобы при
, чтобы при  выполнялось неравенство
выполнялось неравенство  . Ясно, что
. Ясно, что  ибо
ибо  и
и 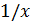 — числа одного знака. Требуемое неравенство верно, если
— числа одного знака. Требуемое неравенство верно, если  или
или  . Следовательно, можно положить
. Следовательно, можно положить 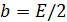 . Тогда из условия
. Тогда из условия  будет вытекать неравенство
будет вытекать неравенство  . Значит, данная функция бесконечно большая при
. Значит, данная функция бесконечно большая при  .
.
Пример 16. Доказать, что
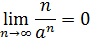 ,
,  .
.
Решение. Если  , то
, то 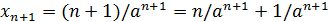 откуда
откуда
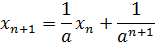 .
.
Заметим, что 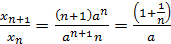 при
при 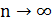 стремится к
стремится к  , причем
, причем 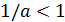 , следовательно, для достаточно больших
, следовательно, для достаточно больших 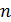 будет выполняться неравенство
будет выполняться неравенство 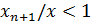 , т.е.
, т.е.  , а тогда последовательность
, а тогда последовательность 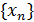 убывающая, а так как она ограничена снизу нулем, то имеет предел. Обозначим его
убывающая, а так как она ограничена снизу нулем, то имеет предел. Обозначим его 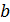 ,
,
 .
.
Если теперь в равенстве  перейти к пределу, то получим
перейти к пределу, то получим
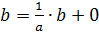 , что выполняется лишь при
, что выполняется лишь при 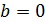 .
.
Замечание. Так как последовательность 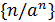 бесконечно малая при
бесконечно малая при  , то последовательность
, то последовательность 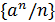 бесконечно большая, т.е.
бесконечно большая, т.е.
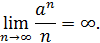
Основные теоремы о пределах.
Теорема 1. Если существует
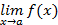 , то он единственный.
, то он единственный.
Теорема 2.
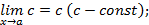
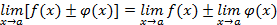

 , если
, если
 .
.
Теорема 3. Если функция 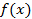 при
при  имеет конечный предел
имеет конечный предел 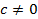 и существует предел функции
и существует предел функции 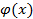 , то
, то
 .
.
Теорема 4. Если в некоторой окрестности точки 
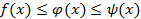 и
и
 то и
то и
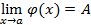 .
.
Теорема 5. Если при некотором 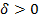 функция
функция 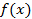 возрастает на
возрастает на 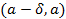 (убывает на
(убывает на 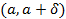 ) и ограничена сверху (снизу), то существует
) и ограничена сверху (снизу), то существует  (
( 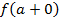 ).
).
Теорема 6. Если для любого 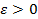 существует
существует 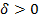 такое, что для произвольных
такое, что для произвольных 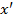 и
и 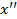 из интервала
из интервала  , отличных от
, отличных от  ,
, 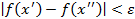 то существует
то существует
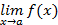 .
.
Теорема 7. Для существования предела
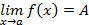 необходимо и достаточно, чтобы всякой последовательности
необходимо и достаточно, чтобы всякой последовательности  , сходящейся к
, сходящейся к  , отвечала последовательность
, отвечала последовательность 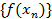 , сходящаяся к
, сходящаяся к  .
.
Теорема 8. Если в некоторой окрестности точки 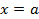 , кроме, может быть, самой этой точки,
, кроме, может быть, самой этой точки, 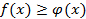 , то и
, то и
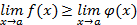 если эти пределы существуют и конечны.
если эти пределы существуют и конечны.
Замечание. Эти теоремы верны и в том случае, когда  не есть конечное число (иногда с очевидными изменениями формулировок.
не есть конечное число (иногда с очевидными изменениями формулировок.
Пример 17. Вычислить
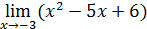 .
.
Решение. По теореме 2
 .
.
Пример 18. Доказать, что последовательность  имеет предел, равный нулю.
имеет предел, равный нулю.
Решение. Заметим, что 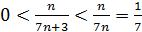 , отсюда
, отсюда
 .
.
По теореме 4 о переходе к переделу в неравенствах получаем
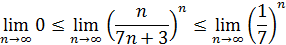
а так как 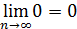 и
и
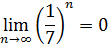 , то
, то
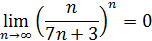 .
.
Пример 19. Доказать, что
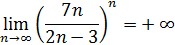
Решение. Заметим, что 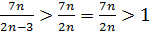 , отсюда
, отсюда  , и по теореме 8 о переходе к пределу в неравенствах
, и по теореме 8 о переходе к пределу в неравенствах
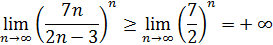 , отсюда
, отсюда
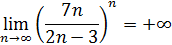 .
.
Пример 20. Вычислить

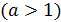 .
.
Решение. Функция, стоящая под знаком предела, по своей конструкции напоминает общий член последовательности из примера 16, и при любом  всегда можно указать такое натуральное число
всегда можно указать такое натуральное число 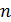 , что
, что 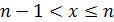 , а следовательно, и
, а следовательно, и  .
.
Теперь, если воспользоваться результатом решения примера 16, то
 и
и
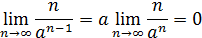
(если
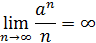 , то
, то 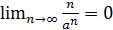 по свойству бесконечно малых и бесконечно больших), а тогда по теореме 4
по свойству бесконечно малых и бесконечно больших), а тогда по теореме 4
 .
.
Замечание. Более короткий и эффективный способ решения этого примера без использования результата решения примера 16 дает правило Лопиталя (см. §4):
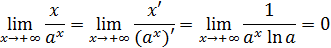 .
.
1. Исходя из определения предела функции, доказать, что:
1) 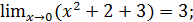 3)
3) 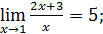 5)
5) 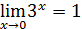 ;
7) ;
7) 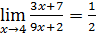 ;
9) ;
9)  ;
11) ;
11) 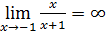 ; ;
| 2) 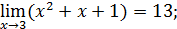 4)
4) 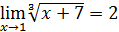 ;
6) ;
6)  ;
8) ;
8) 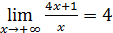 ;
10) ;
10) 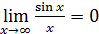 ;
12) ;
12) 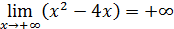 . .
|
2. Исходя из определения предела числовой последовательности, доказать, что:
1) 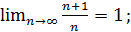 3)
3) 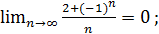 5)
5)  7)
7) 
| 2)  4)
4)  ;
6) ;
6) 
|
3. Используя основные теоремы, вычислить следующие пределы:
1)  3)
3) 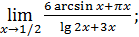 5)
5) 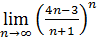 ;
7) ;
7) 
| 2)  4)
4)  ;
6) ;
6) 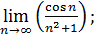
|
4. Вычислить пределы следующих последовательностей, заданных рекуррентными формулами:
1)  3)
3) 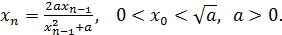
| 2) 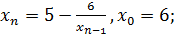
|
5. Доказать, что следующие переделы не существуют:
1) 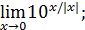 3)
3) 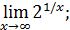
| 2) 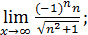 4)
4) 
|
ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ.
ЭЛЕМЕНТАРНЫЕ ПРИЕМЫ И ИСПОЛЬЗОВАНИЕ
ЗАМЕЧАТЕЛЬНЫХ ПРЕДЕЛОВ
1. Понятие неопределенности. В практике отыскания пределов наиболее часто применяется теорема 2 об арифметических действиях над пределами (см. § 1). Однако ее непосредственное применение бывает невозможно в особых ситуациях, называемых неопределенностями, которые возникают при нарушении ее условий. Например, если 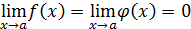 , то нельзя сказать ничего определенного о пределе
, то нельзя сказать ничего определенного о пределе 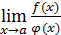 , не зная конкретного вида функции
, не зная конкретного вида функции  и
и 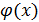 . В этом случае говорят о наличии неопределенного вида
. В этом случае говорят о наличии неопределенного вида  . Неопределенность возникает и при отыскании предела
. Неопределенность возникает и при отыскании предела 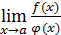 , если
, если  ,
, 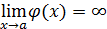 (
(  и
и 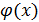 могут быть бесконечно большими определенного знака или нет). Ее обозначают символом
могут быть бесконечно большими определенного знака или нет). Ее обозначают символом 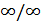 . Еще один пример: ищется
. Еще один пример: ищется 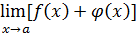 , причем
, причем  и
и 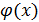 – бесконечно большие противоположных знаков – здесь неопределенность
– бесконечно большие противоположных знаков – здесь неопределенность 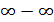 . При вычислении предела
. При вычислении предела  создается неопределенность
создается неопределенность 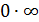 , если
, если 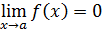 ,
, 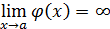 . Кроме этих неопределенностей, связанных с арифметическими действиями над пределами, существуют неопределенности
. Кроме этих неопределенностей, связанных с арифметическими действиями над пределами, существуют неопределенности 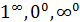 , относящиеся к пределу вида
, относящиеся к пределу вида 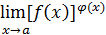 .
.
Чтобы найти пределы при наличии неопределенности, надо эту неопределенность устранить, открыв тем самым возможность использования тех или иных теорем о пределах. Это достигается, с одной стороны, применением алгебраических и тригонометрических преобразований (разложение функций на множители или на слагаемые, приведение дробей к общему знаменателю, добавление и вычитание некоторого выражения, умножение и деление на некоторую функцию, вынесение множителя за скобку и т.п.), заменой переменной, использованием эквивалентных бесконечно малых и бесконечно больших (см. § 3), а с другой стороны, использованием так называемых замечательных пределов.
I. 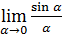 .
.
II. 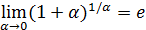 (
( 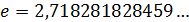 — иррациональное число. Оно является основанием системы логарифмов, называемых натуральными. Вместо
— иррациональное число. Оно является основанием системы логарифмов, называемых натуральными. Вместо 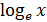 принято писать
принято писать 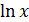 ).
).
Из предела II выводятся следующие пределы, широко применяемые при раскрытии неопределенностей:
III. 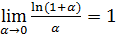 .
.
IV.  (в частности,
(в частности, 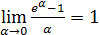 ).
).
V. 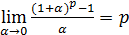 .
.
Замечание. Применение замечательных пределов требует понимания и запоминания структуры каждого из них и при этом необходимости ее воспроизведения. Так, для предела 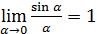 характерно отношение синуса бесконечно малого угла к самому углу. Поэтому всякий предел вида
характерно отношение синуса бесконечно малого угла к самому углу. Поэтому всякий предел вида  равен 1, если
равен 1, если  . Например, каждый из пределов
. Например, каждый из пределов  ,
,  ,
, 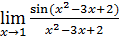 есть, в сущности, первый замечательный предел и потому равен 1, чего нельзя сказать ни об одном из пределов
есть, в сущности, первый замечательный предел и потому равен 1, чего нельзя сказать ни об одном из пределов 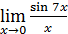 ,
,  ,
, 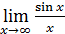 .
.
Для предела 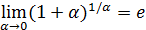 характерно, что сумма, равная единице плюс бесконечно малая, возводится в степень, обратную этой бесконечно малой. Следовательно, если
характерно, что сумма, равная единице плюс бесконечно малая, возводится в степень, обратную этой бесконечно малой. Следовательно, если  , то и
, то и 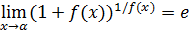 . Такова структура каждого из пределов
. Такова структура каждого из пределов 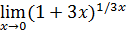 ,
, 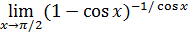 ,
, 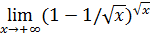 , и потому все они равны
, и потому все они равны 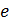 , но структура пределов
, но структура пределов 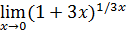 ,
, 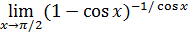 ,
,  отлична от срукткры замечательного предела.
отлична от срукткры замечательного предела.
Подобные рассуждения справедливы и для пределов III–V.
Заметим, что если заданный предел не обладает структурой ни одного из пределов I–V, это не исключает возможности использования их для его отыскания.
2. Неопределенность 0/0. В простейших случаях такая неопределенность устраняется путем выделения в числителе и знаменателе общего множителя, создающего неопределенность, и сокращения на него, после чего можно применять теорему о пределе частного. Этот прием основан на теореме: если в окрестности точки 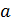
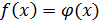 для всех
для всех 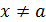 и существует один из пределов
и существует один из пределов 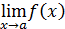 или
или  , то существует и другой, и они равны. Например, функции
, то существует и другой, и они равны. Например, функции  и
и  равны при
равны при  . Поскольку
. Поскольку 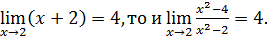
Способ выделения общего множителя, да и сам его вид зависят от структуры числителя и знаменателя. Иногда вид выделяемого множителя зависит от способа его выделения (см. ниже пример 5). Для раскрытия неопределенности 0/0 применяются и другие элементарные приемы, а также пределы I, III–V, используются эквивалентные бесконечно малые.
Пример 1. Вычислить 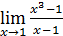 .
.
Решение. Многочлены, стоящие в числителе и знаменателе, обращаются в нуль при  . По теореме Безу каждый из них должен делиться на
. По теореме Безу каждый из них должен делиться на 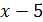 , т.е. каждый из них может быть представлен в виде произведения
, т.е. каждый из них может быть представлен в виде произведения 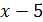 на некоторый многочлен.
на некоторый многочлен.
Таким образом, нахождение предела сводится прежде всего к выделению в числителе и знаменателе множителя 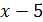 , незримое присутствие которого и создает неопределенность 0/0. Практически это достигается каким-либо способом разложения числителя и знаменателя на множители, например делением «уголком»*.
, незримое присутствие которого и создает неопределенность 0/0. Практически это достигается каким-либо способом разложения числителя и знаменателя на множители, например делением «уголком»*.
[ДЕЛЕНИЕ СТОЛБИКОМ]
Теперь искомый предел можно представить в виде
 .
.
Неопределенность исчезла. По теореме о пределе частного находим ответ:  .
.
Замечание. Веденный пример решения всегда приводит к цели, когда ищется  , где
, где 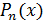 и
и  — многочлены степеней m и n относительно x. Можно применить и непосредственное разложение многочленов на множители путем группировки слагаемых с выделением множителя
— многочлены степеней m и n относительно x. Можно применить и непосредственное разложение многочленов на множители путем группировки слагаемых с выделением множителя 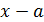 , если такая группировка очевидна. В приведенном примере такое разложение легко получить для числителя:
, если такая группировка очевидна. В приведенном примере такое разложение легко получить для числителя:
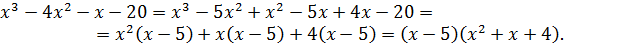
1. Раскрыть неопределенность 0/0:
1)  ;
3) ;
3)  5)
5)  ;
7) ;
7) 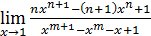 (m и n – натуральные числа);
9)
(m и n – натуральные числа);
9) 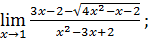 11)
11) 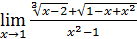 ;
13) ;
13) 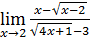 ;
15) ;
15) 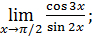 17)
17) 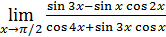 ;
19) ;
19) 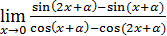 ( (  );
21) );
21)  23)
23) 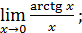 25)
25)  27)
27) 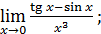 29)
29) 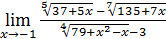 ;
31) ;
31) 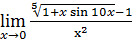 ;
33) ;
33)  (n – натуральное число);
35)
(n – натуральное число);
35) 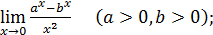 37)
37) 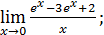 39)
39)  ;
41) ;
41) 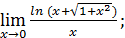 43)
43)  45)
45) 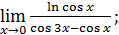 47)
47) 
| 2) 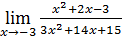 ;
4) ;
4)  ;
6) ;
6)  ;
8) ;
8) 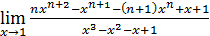 (n – натуральное число);
10)
(n – натуральное число);
10) 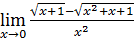 ;
12) ;
12) 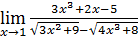 ;
14) ;
14)  ;
16) ;
16) 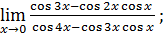 18)
18) 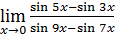 ;
20) ;
20)  ;
22) ;
22)  24)
24)  26)
26)  28)
28)  30)
30) 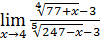 ;
32) ;
32)  ;
34) ;
34)  36)
36) 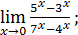 38)
38) 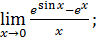 40)
40) 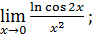 42)
42) 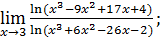 44)
44) 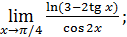 46)
46) 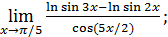 48)
48) 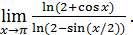
|
3. Неопределенность ∞ / ∞ . Эта неопределенность раскрывается теми же методами, что и неопределенность 0/0, а иногда просто сводится к последней элементарными преобразованиями.
Пример 3. Вычислить 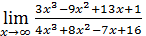 .
.
Решение. При достаточно больших значениях 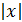 величина числителя определяется членом
величина числителя определяется членом 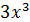 , а роль остальных слагаемых тем незначительней, чем больше
, а роль остальных слагаемых тем незначительней, чем больше 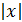 . В знаменателе при росте
. В знаменателе при росте 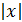 доминирующее значение приобретает слагаемое
доминирующее значение приобретает слагаемое 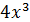 . Поэтому именно присутствие членов, содержащих
. Поэтому именно присутствие членов, содержащих  , является причиной возникновения неопределенности ∞/∞. Если в числителе и знаменателе вынести множитель
, является причиной возникновения неопределенности ∞/∞. Если в числителе и знаменателе вынести множитель  за скобки и сократить на него, то неопределенность исчезнет:
за скобки и сократить на него, то неопределенность исчезнет:
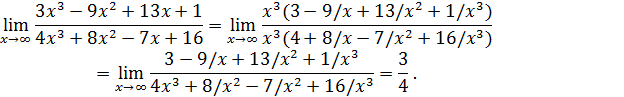
(Слагаемые 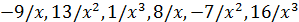 есть бесконечно малые при
есть бесконечно малые при  ).
).
Замечание. Проведенные преобразования фактически сводятся к делению числителя и знаменателя на старшую степень x. Часто этого бывает достаточно для раскрытия неопределенности ∞/∞. (В сущности, к этому же премк можно отнести замену переменной  . Тогда
. Тогда 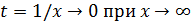 и
и

Пример 4. Вычислить 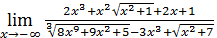 .
.
Решение. Воспользуемся замечанием к примеру 15. Заметив, что старшая степень 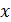 в данном случае равна 3, разделим почленно ислитель и знаменатель на
в данном случае равна 3, разделим почленно ислитель и знаменатель на  :
:

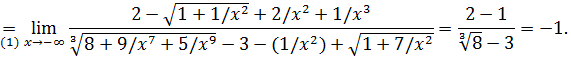
(Смена знака перед двумя радикалами в переходе (1) объясняется тем, что при 
 и аналогично
и аналогично 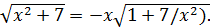
Пример 5. Вычислить 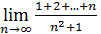 .
.
Решение. В числителе стоит сумма членов арифметической прогрессии. Следовательно, 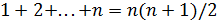 и
и

Пример 6. Вычислить 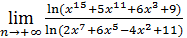 .
.
Решение. Множителем, создающим неопределенность, в данном примере является 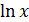 , что видно из равенств
, что видно из равенств
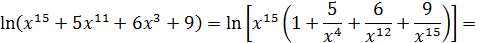
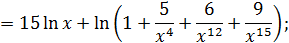
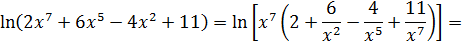

Заменив числитель и знаменатель правыми частями этих равенств и поделив их затем на 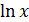 , добьемся исчезновения неопределенности:
, добьемся исчезновения неопределенности:

2. Раскрыть неопределенность ∞/∞:
| 49) | 1) 
| 2) 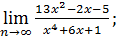
| 3) 
|
Вывести простое правило вычисления предела  , где
, где 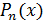 и
и 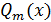 – многочлены степеней n и m.
– многочлены степеней n и m.
50) 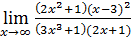 ;
52) ;
52)  54)
54) 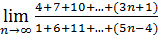 ;
56) ;
56)  ;
58) ;
58) 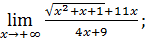 60)
60) 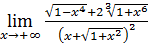 ;
62) ;
62)  ;
64) ;
64) 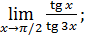 66)
66) 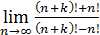 ;
68) ;
68)  ;
70) ;
70) 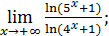
| 51) 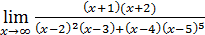 ;
53) ;
53)  ;
55) ;
55) 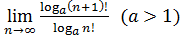 ;
57) ;
57)  ;
59) ;
59)  ;
61) ;
61) 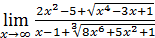 ;
63) ;
63) 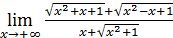 ;
65) ;
65)  67)
67) 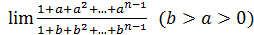 ;
69) ;
69) 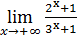 ;
71) ;
71) 
|
4. Неопределенность  . Неопределенности такого вида элементарными преобразованиями, использованием замечательных пределов или заменой переменной сводятся к одной из неопределенностей вида 0/0 или ∞/∞.
. Неопределенности такого вида элементарными преобразованиями, использованием замечательных пределов или заменой переменной сводятся к одной из неопределенностей вида 0/0 или ∞/∞.
Пример 7. Вычислить  .
.
Решение.

Пример 8. Вычислить 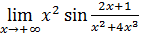 .
.
Решение. Заметив, что при 
 , выделим замечательны предел I:
, выделим замечательны предел I:
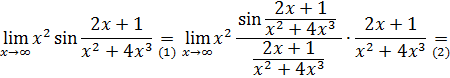

После выделения замечательного предела I делением и умножением на 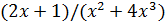 (переходы (1) – (3)) неопределенность
(переходы (1) – (3)) неопределенность 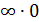 свелась к неопределенности
свелась к неопределенности 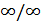 , ликвидация которой произведена делением числителя и знаменателя на старшую степень переменной (переход (4)).
, ликвидация которой произведена делением числителя и знаменателя на старшую степень переменной (переход (4)).
Вычислить следующие пределы:
72) 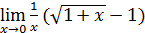 ;
74) ;
74) 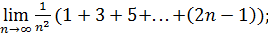 76)
76) 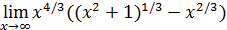 ;
78) ;
78) 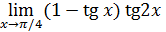 ;
80) ;
80) 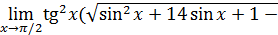
 82)
82) 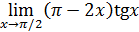 ;
84) ;
84)  ;
86) ;
86)  88)
88) 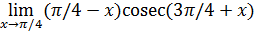 ; ;
| 73) 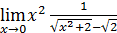 ;
75) ;
75)  ;
77) ;
77) 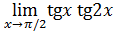 ;
79) ;
79) 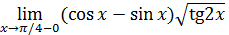 ;
81) ;
81) 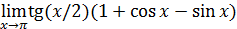 ;
83) ;
83) 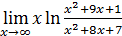 ;
85) ;
85) 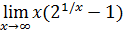 ;
87) ;
87) 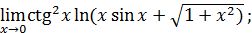
|
5. Неопределенность 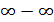 . Раскрытие этой неопределенности, нередко сопряженное с большими трудностями, достигается использованием замечательных пределов или сведением к одной из неопределенностей 0/0, ∞/∞,
. Раскрытие этой неопределенности, нередко сопряженное с большими трудностями, достигается использованием замечательных пределов или сведением к одной из неопределенностей 0/0, ∞/∞, 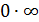 с помощью элементарных преобразований.
с помощью элементарных преобразований.
Пример 9. Вычислить 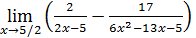 .
.
Решение. Приведение дробей к общему знаменателю сменяет неопределенность 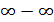 на неопределенность 0/0, которая раскрывается сокращением дроби на множитель
на неопределенность 0/0, которая раскрывается сокращением дроби на множитель  . Действительно, учитывая, что
. Действительно, учитывая, что  , находим последовательно
, находим последовательно

∞/∞, 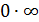 с помощью элементарных преобразований.
с помощью элементарных преобразований.
Пример 10. Вычислить 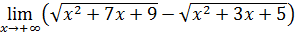 .
.
Решение. Умножение и деление на одно и то же выражение, сопряженное данному двучлену, сводит неопределенность 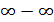 к неопределенности
к неопределенности 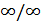 :
:

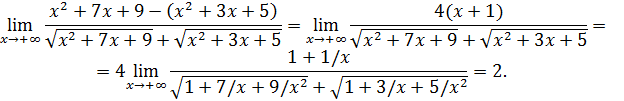
89)  ;
91) ;
91) 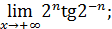
| 90) 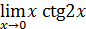 ;
92) ;
92) 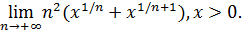
|
5. Неопределенность 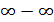 . Раскрытие этой неопределенности, нередко сопряженное с большими трудностями, достигается использованием замечательных пределов или сведением к одной из неопределенностей 0/0, ∞/∞,
. Раскрытие этой неопределенности, нередко сопряженное с большими трудностями, достигается использованием замечательных пределов или сведением к одной из неопределенностей 0/0, ∞/∞, 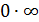 с помощью элементарных преобразований.
с помощью элементарных преобразований.
Пример 11. Вычислить 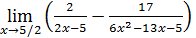 .
.
Решение. Приведение дробей к общему знаменателю сменяет неопределенность 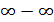 на неопределенность 0/0, которая раскрывается сокращением дроби на множитель
на неопределенность 0/0, которая раскрывается сокращением дроби на множитель  . Действительно, учитывая, что
. Действительно, учитывая, что  , находим последовательно
, находим последовательно

∞/∞, 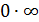 с помощью элементарных преобразований.
с помощью элементарных преобразований.
Пример 12. Вычислить 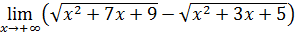 .
.
Решение. Умножение и деление на одно и то же выражение, сопряженное данному двучлену, сводит неопределенность 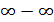 к неопределенности
к неопределенности 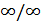 :
:

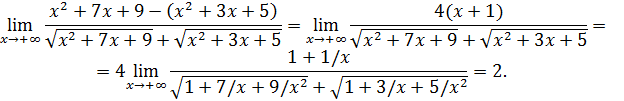
Вычислить следующие пределы:
93)  ; ;
| 94) 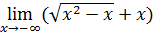 ; ;
|
95)  ; ;
| 96)  ; ;
|
97) 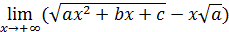 ; ;
| 98) 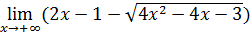 ; ;
|
| 99)
| |
| 100)
| |
| 101)
| |
| 102)
| |
| 103)
| |
104) 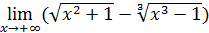 ; ;
| 105) 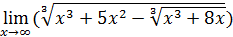 ; ;
|
| 106)
| |
107)  ; ;
| 108) 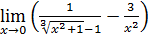 ; ;
|
109) 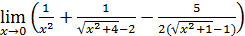 ; ;
| 110) 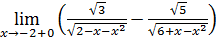 ; ;
|
111) 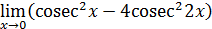 ; ;
| 112)  ; ;
|
113) 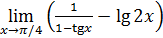 ; ;
| 114)  ; ;
|
115)  ; ;
| 116)  ; ;
|
117)  ; ;
| 118) 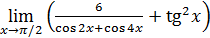 ; ;
|
119) 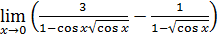 ; ;
| 120)  ; ;
|
6. Неопределенность 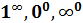 . Условия, при которых возникают эти неопределенности, связанные с пределом
. Условия, при которых возникают эти неопределенности, связанные с пределом 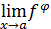 , где
, где 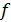 и
и 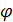 — функции от x, можно пояснить таблицей:
— функции от x, можно пояснить таблицей:

| 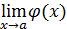
| 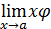
|
| 1 | 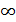
| 
|
| 0 | 0 | 
|
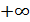
| 0 | 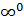
|
Из тождества  и непрерывности показательной функции (см. главу III) следует, что
и непрерывности показательной функции (см. главу III) следует, что  . Таким образом, раскрытие неопределенностей
. Таким образом, раскрытие неопределенностей 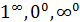 сводится к отысканию предела функции
сводится к отысканию предела функции  , который связан с неопределенностью
, который связан с неопределенностью 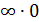 , как это видно из таблицы. Если S найдено, то
, как это видно из таблицы. Если S найдено, то  . Заметим, что
. Заметим, что 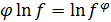 . Следовательно, для раскрытия любой из неопределенностей рассматриваемых типов достаточно найти предел натурального логарифма функции, стоящей под знаком предела, и по его значению S восстановить искомый предел
. Следовательно, для раскрытия любой из неопределенностей рассматриваемых типов достаточно найти предел натурального логарифма функции, стоящей под знаком предела, и по его значению S восстановить искомый предел 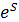 . Неопределенность
. Неопределенность  может быть раскрыта помимо изложенного способа, общего для этих неопределенностей, способом непосредственной «подгонки» к замечательному пределу II
может быть раскрыта помимо изложенного способа, общего для этих неопределенностей, способом непосредственной «подгонки» к замечательному пределу II  , например, по такой схеме:
, например, по такой схеме:

Выражение, построенное внутри квадратных скобок, имеет вид 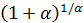 , где
, где  — бесконечно малая при
— бесконечно малая при 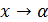 . Нахождение предела
. Нахождение предела
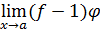 требует раскрытия неопределенности
требует раскрытия неопределенности 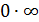 .
.
Пример 13. Вычислить  .
.
Решение. Поскольку 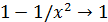 при
при  , то имеем неопределенность вида
, то имеем неопределенность вида 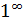 . Выделим замечательный предел II:
. Выделим замечательный предел II:

Пример 14. Вычислить 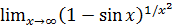 .
.
Решение.  при
при 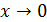 стремится к единице, а
стремится к единице, а 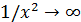 , следовательно, здесь неопределенность вида
, следовательно, здесь неопределенность вида  . Выделим замечательный предел II:
. Выделим замечательный предел II:
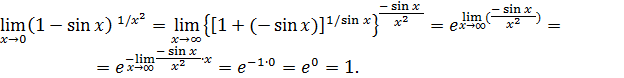
Пример 15. Вычислить 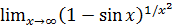 .
.
Решение.  при
при 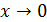 стремится к единице, а
стремится к единице, а 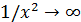 , следовательно, здесь неопределенность вида
, следовательно, здесь неопределенность вида  . Выделим замечательный предел II:
. Выделим замечательный предел II:
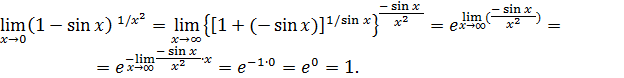
Пример 16. Вычислить 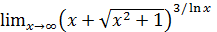 .
.
Решение.  при
при 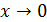 стремится к единице, а
стремится к единице, а 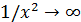 , следовательно, здесь неопределенность вида
, следовательно, здесь неопределенность вида 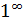 . Выделим замечательный предел II:
. Выделим замечательный предел II:
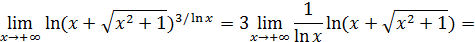
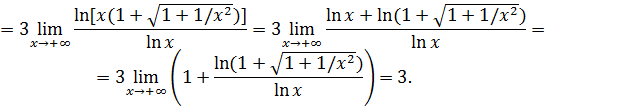
Следовательно, 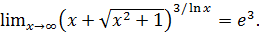
Вычислить:
121) 
| 122) 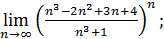
|
123) 
| 124) 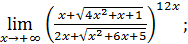
|
125) 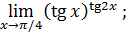
| 126) 
|
127) 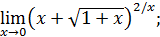
| 128) 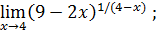
|
129) 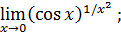
| 130) 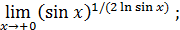
|
131) 
| 132) 
|
133) 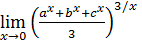
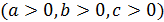 ; ;
| 134) 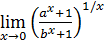
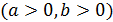 ; ;
|
135) 
| 136) 
|
137) 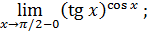
| 138) 
|
139) 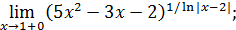
| 140) 
|
141) 
| 142) 
|
143) 
| 144) 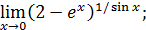
|
145) 
|
СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ
И БЕСКОНЕЧН БОЛЬШИХ.
Дата добавления: 2021-06-02; просмотров: 172; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

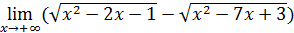 ;
;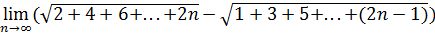 ;
;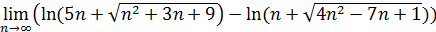 ;
;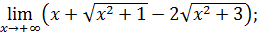
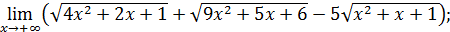
 ;
;