Основное логарифмическое тождество
Логарифмы
Использование логарифмов позволяет заменить умножение на значительно более простое сложение, деление — на вычитание, а возведение в степень и извлечение корня заменяются соответственно на умножение и деление на показатель степени числа.
История логарифмов, применение, интересные факты
Толчком к применению логарифмов стало свойство степеней: при перемножении степеней с одинаковыми основаниями степени складываются: 
. В 8 веке индийский математик Вирасена представил таблицу целочисленных показателей (т.е. логарифмов) оснований 2, 3 и 4. В начале 17 века шотландский математик Джон Непер (1550 - 1617) опубликовал сочинение "Описание удивительной таблицы логарифмов", в котором кратко было описано понятие логарифма, свойства. Термин "логарифм", предложенный ученым, прижился. Теория логарифмов была представлена Непером в книге "Построение удивительной таблицы логарифмов". На разработку теории логарифмов Непера толкнули громоздкие астрологические расчеты. Основным свойством логарифма Непера было следующее свойство: если данные величины образую геометрическую прогрессию, то логарифмы этих величин образую арифметическую.
Через несколько лет после выхода книги Непера появились логарифмические таблицы, использующие более близкое к современному понимание логарифма. В 1617 году английский математик Генри Бригс (1561 - 1630) издал 14-значные таблицы десятичных логарифмов. Двумя годами позже лондонский учитель математики Джон Спайделл переиздал таблицы Непера, внеся в них исправления и дополнения.
|
|
|
До конца 19 века общепринятого обозначения логарифма не было, основание 
указывалось то левее и выше символа 
, то над ним. В итоге математики пришли к выводу, что наиболее удобное место для основания - ниже строки, после символа , т.е. современный вариант 
. Обозначения десятичного и натурального логарифмов lg, ln появились намного раньше в работах сразу нескольких ученых, но окончательно также закрепились где-то в конце 19 века.
Операция логарифмирования впервые появилась в работах английского математика Джона Валлиса (1616 - 1703) и швейцарского ученого Иоганна Бернулли (1667 - 1748), а окончательно закрепилось после работы Леонарда Эйлера (1707 - 1783) "Введение в анализ бесконечных".
Свое применение и развитие теория логарифмов нашла в рекурсивных алгоритмах, теории фракталов, в теории чисел и математическом анализе, в статистике и теории вероятностей, информатике и вычислительной технике, механике и физике, химии, теории музыки, психологии и философии.
Определение
Логарифмом числа 
по основанию ( ) называется такое число 
, что 
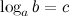, то есть записи 
и равносильны. Логарифм имеет смысл, если 
.
|
|
|
Другими словами Логарифм числа по основанию определяется как показатель степени, в которую надо возвести число , чтобы получить число (Логарифм существует только у положительных чисел).
Логарифм в переводе с греческого буквально означает "число, изменяющее отношение".
Специальные обозначения:
1. Натуральный логарифм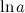 
- логарифм по основанию 
, где - число Эйлера.
2. Десятичный логарифм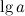 
- логарифм по основанию 10.
Свойства логарифмов
1°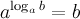 
- основное логарифмическое тождество.
2°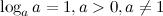 
3°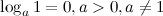 
Логарифм единицы по любому положительному, отличному от 1, основанию равен нулю. Это возможно потому, что из любого действительного числа можно получить 1 только возведя его в нулевую степень.
4°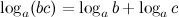 
- логарифм произведения.
Логарифм произведения равен сумме логарифмов сомножителей.
5° 
- логарифм частного.
Логарифм частного (дроби) равен разности логарифмов сомножителей.
6°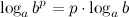 
- логарифм степени.
Логарифм степени равен произведению показателя степени на логарифм ее основания.
7°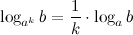 
8°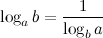 
9°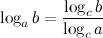 
- переход к новому основанию.
Основное логарифмическое тождество
Показательное уравнение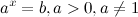 
не имеет решений при 
и имеет единственный корень в случае, когда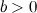 
. Этот корень называют логарифмом числа по основанию и обозначают , то есть
|
|
|
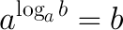
Выражение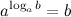 
с учетом того, что называется - основным логарифмическим тождеством.
Дата добавления: 2021-06-02; просмотров: 78; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!