Вероятность события. Сложение вероятностей.
Сочетания без повторений. Бином Ньютона
Сочетаниями из n элементов по m в каждом (m ≤ n) называются такие соединения, каждое из которых содержит m элементов, взятых из данных n различных элементов, и которые отличаются одно от другого по крайней мере одним элементом.
Иногда такие сочетания называют сочетаниями без повторений.
Число всевозможных сочетаний из n различных элементов по m элементов обозначают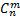 
Формула для подсчёта числа сочетаний:
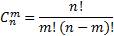
Используя данную формулу можно отметить основные свойства сочетаний.
Простейшие свойства сочетаний:
1) 
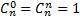
2) 
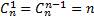
3) 
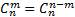
При возведении суммы или разности двух чисел во вторую или третью степень мы пользовались формулами сокращенного умножения, которые являются частным случаем бинома Ньютона.
Бином Ньютона – формула разложения произвольной натуральной степени двучлена в многочлен.
Числа 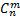являются коэффициентами в формуле бинома Ньютона:
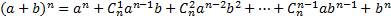
Пример 1.
В вазе лежат двенадцать конфет, четыре из которых шоколадные, а остальные карамель. Вы хотите угоститься, выбрав две шоколадные и три карамельные конфеты. Сколькими способами вы можете это сделать?
Решение :
Мы имеем два события. Это выбор шоколадных и выбор карамельных конфет. Порядок конфет не важен. Поэтому мы можем использовать формулу сочетания для каждого из событий. Так, как шоколадных конфет всего четыре, а выбрать мы хотим две, то это можно сделать способами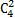 
.
|
|
|
1) 
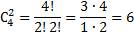
Теперь посчитаем количество выбора карамельных конфет. Их общее количество в вазе 12-4=8, а выбрать мы хотим три. Рассчитаем сочетание из восьми по три.
2) 
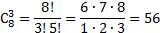
События выбора разных видов конфет между собой независимы, поэтому по правилу умножения получаем
3) 
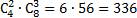
Ответ: 336
Пример 2.
Представить разложение двучлена в n степени в виде многочлена, где n=0, 1, 2, 3
Решение:
Первые четыре разложения мы хорошо умеем делать, используя формулы квадрата и куба разности.
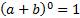
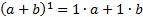
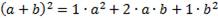
Сочетания с повторениями.
Выбор m элементов из множества, содержащего n элементов с повторением и без упорядочивания выбранных элементов в последовательную цепочку называют сочетаниями с повторениями из n элементов по m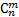 
Пусть множество содержит n элементов, а выборка будет содержать m элементов. Аналогично тому, как мы делали в примере, зашифруем каждую выборку единицами и нулями.
Число единиц равно числу выбираемых элементов, то есть m. Поскольку всего различных элементов в множестве n, то мы должны поставить между единицами (n-1) «перегородку», то есть (n-1) нулей. Число размещений с повторениями 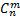равно числу перестановок с повторениями элементов полученного множества из m единиц и (n-1) нулей
|
|
|
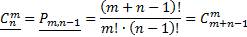
Сочетания с повторениями используем тогда, когда порядок расположения элементов в выборке не имеет значения и элементы могут повторяться
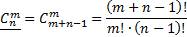
Пример 1.
Сколько существует треугольников, длины сторон которых принимают одно из следующих значений: 5, 6, 7, 8, 9?
Решение:
Данные стороны таковы, что любые три из них соответствуют правилу треугольника, т.е. каждая сторона меньше суммы двух других. Значит, любая комбинация из трех сторон образует треугольник. Здесь речь идет о числе сочетаний из 5 элементов по 3 с повторениями:
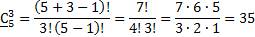
Ответ: 35
Пример 2.
Сколько всего чисел (не больше 100000) можно составить из цифр 1, 2, 3, 4 и 5 в каждом из которых цифры расположены в неубывающем порядке?
Решение. Это задача о числе сочетаний из пяти цифр по одному, по два, по три, по четыре и по пяти с повторениями в каждом случае.
Поскольку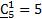 
, 
, 
, 
, 
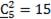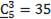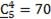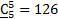, то существует 5+15+35+70+126=251 чисел, удовлетворяющих условию задачи.
Ответ: 126
Вероятность события. Сложение вероятностей.
Теория вероятностей – раздел математики, изучающий случайные события, случайные величины, их свойства и операции над ними. Рассмотрим некоторые ключевые понятия, которые используются в теории вероятностей.
|
|
|
Испытанием называется осуществление определенных действий.
Событие- факт, который может произойти в результате испытания.
Любой результат испытания называется исходом.
Достоверным называют событие, которое в результате испытания обязательно произойдёт.
Невозможным называют событие, которое заведомо не произойдёт в результате испытания.
Пространство элементарных событий Ω — множество всех различных исходов произвольного испытания.
Если события не могут произойти одновременно в одном испытании, то события называются несовместными.
Противоположное событие происходит тогда, когда исходное событие А не происходит.
Полной группой событий называется такая система событий, что в результате испытания непременно произойдет одно и только одно из них.
Число испытаний, в которых событие наступило, назовем абсолютной частотой и обозначим n. Общее число произведенных испытаний обозначим N.
Отношение абсолютной частоты к числу испытаний n/N называется относительной частотой события.
Относительная частота показывает, какая доля испытаний завершилась наступлением данного события. Эта относительная частота и определяет вероятность случайного события. Её ещё называют статистической вероятностью события.
|
|
|
Равновозможные события - такие события, для которых нет никаких объективных оснований считать, что одно является более возможным, чем другие.
Суммой событий А и В называется событие А+В, которое состоит в том, что наступит или событие А, или событие В, или оба события одновременно.
Произведением событий А и В называется событие А•В, состоящее в совместном осуществлении событий А и В.
События обычно обозначаются заглавными буквами латинского алфавита (А, В, С, D,…).
Например:
1. Пусть А - идет дождь, B - идет снег, тогда А + В – «идет снег или дождь»
2. При 3-х выстрелах по мишени события: А0 – «попаданий нет», А1 – «одно попадание», А2 – «два попадания», тогда А=А0+А1+А2 - «произошло не больше двух попаданий»
3. Пусть С - из урны вынули белый шар, D - из урны вынули белый шар, тогда C⋅D - из урны вынули два белых шара
4. Пусть С - из урны вынули белый шар, D - из урны вынули белый шар, тогда C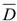 
⋅- из урны вынули два шара: белый и не белый
Теорема сложения вероятностей несовместных событий: вероятность появления одного из двух несовместных событий А или В равна сумме вероятностей этих событий:
Р(А+В)=Р(А)+Р(В)
Пример 1.
Известна история о том, как однажды к Г. Галилею явился солдат и попросил помочь ему в решении насущного вопроса: какая сумма 9 или 10 очков при бросании трех костей выпадает чаще?
Может показаться, что шансы равны, так как каждая сумма из 9 и 10 очков может быть получена одним их шести способов:
9 = 1 + 2 + 6 = 1 + 3 + 5 = 1 + 4 + 4 = 2 + 2 + 5 = 2 + 3 + 4 = 3 + 3 + 3;
10 = 1 + 3 + 6 = 1 + 4 + 5 = 2 + 2 + 6 = 2 + 3 + 5 = 2 + 4 + 4 = 3 + 3 + 4.
Однако с учетом перестановок для суммы 9 очков получается 25 различными способами (по 6 способов для первого, второго, пятого вариантов суммы, по 3 способа для третьего и четвертого вариантов, 1 способ для последнего варианта 6 + 6 + 3 + 3 + 6 + 1), а для суммы 10 очков – 27 различными способами (6 + 6 + 3 + 6 + 3 + 3). Как видно, шансы этих случайных событий довольно близки между собой и относятся друг к другу как 25:27, что и вызвало затруднения солдата.
Таким образом, чаще выпадает сумма 10.
Дата добавления: 2021-06-02; просмотров: 135; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!