Графическое изображение вариационного ряда
Занятие 10
Тема: Статистические методы изучения изменчивости. Построение вариационного ряда
Предметом вариационной статистики служит группа биологических объектов (совокупность) составляющих вид, породу, стада животных, линии, семейства, количество эритроцитов в определенном объеме крови животного и т.д. Совокупность состоит из членов или единиц. Для стада коров единицей является каждая корова.
При изучении биологических явлений используют статистические методы обработки данных. Особенно большое значение биометрическая обработка приобретает при решении теоретических и практических вопросов генетики, селекции, ветеринарии.
Цель занятия – научиться составлять вариационные ряды, изображать их графически и на основании этого делать заключение об изменчивости и наследуемости признаков.
Основные термины:
Вариационная статистика (биометрия, биологическая статистика) – наука о способах применения математических методов в биологии.
Объект совокупности (n) - число единиц входящее в совокупность.
Варианта (V) — величина изучаемого признака для каждой единицы совокупности.
Количественные признаки – изучают путем измерений и выражают цифрами, например: удой, живая масса, настриг шерсти и др.
Качественные признаки описываются словами, например: масть – черная, красная; животное больное и т.д.
Генеральная совокупность – это группа животных, составляющих вид, породу, например: коровы красной степной породы, свиньи крупной белой породы.
Выборочная совокупность (выборка) – это гpyппa животных, отобранная из генеральной совокупности по принципу случайности. Выборки бывают: многочисленными (n>30) и малочисленными (n<30) или их еще называют большие и малые выборки.
Статистическая обработка многочисленной (большой) выборки начинается из составления вариационного ряда.
Вариационный ряд – это ряд чисел сгруппированных в классы в зависимости от величины изучаемого признака. Он отображает, как происходит изменение признака от минимальной до максимальной величины, какая частота вариант в каждом классе.
Модальный класс – это класс, в котором встречается наибольшее число вариант выборочной совокупности.
Методика построения вариационного ряда
1. Из всей выборки найти лимиты (lim) т.е. максимальную (max) и минимальную (min) величину и разность между ними (max – min).
2. Определить предварительное количество классов, которое зависит от объема выборки:
| Число вариант | 25-46 | 47-93 | 94-187 | 188-377 | 378-755 |
| Число классов | 6 | 7 | 8 | 9 | 10 |
3. Определить классовый промежуток (k) путем деления разности между max и min на предполагаемое число классов, исходя из наличия вариант в совокупности:
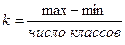
4. Установить начало классов, для чего к минимальному значению признака прибавляют классовый промежуток (k), пока не включится максимальное значение признака.
5. Установить верхние границы классов путем вычитания из нижней границы каждого последующего класса единицы, если точность измерения признака в целых числах; 0,1 – если точность измерения признака до десятых и т.д.
6. Последовательно, начиная с первой варианты, разнести их все по классам, применяя метод конверта:
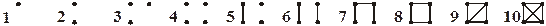 .
.
Пример. На одной из ферм хозяйства определяли живую массу телят при рождении у 51 теленка красной степной породы (кг). Каждое животное характеризовалось следующими показателями:
| 28, | 31, | 30, | 33, | 23, | 20, | 33, | 20, | 26, | 25, | 27, | 26, | 34, | 24, |
| 35, | 42, | 28, | 24, | 27, | 22, | 26, | 42, | 31, | 35, | 30, | 22, | 26, | 39, |
| 39, | 36, | 28, | 27, | 29, | 29, | 28, | 29, | 33, | 32, | 34, | 28, | 26, | 29, |
| 29, | 28, | 34, | 30, | 33, | 36, | 32, | 31, | 34. |
Для построения вариационного ряда, согласно вышеизложенной методики, производим следующие расчеты:
1. n = 51; max = 42; min = 20,
разность между лимитами lim = 42 – 20 = 22.
2. Предварительное число классов – 7.
3. Находим классовый промежуток:
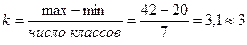 .
.
4. Находим нижние границы классов, min:
min + k; 20 + k или 20 + 3 = 23; 23 + 3 = 26;
26 + 3 = 29; 29 + 3 = 32; 32 + 3 = 35; 35 + 3 = 38; 38 + 3 = 41; 41 + 3 = 44.
5. Находим верхние границы классов, min-1:
23 – 1 = 22; 26 – 1 = 25; 29 – 1 = 28; 32 – 1 = 31; 35 – 1 = 34; 38 – 1 = 37; 41 – 1 = 40; 44 – 1 = 43.
6. Последовательно, начиная с первой варианты разносим их методом конверта по классам (табл).
Таблица – Построение вариационного ряда
| Границы | 20-22 | 23-25 | 26-28 | 29-31 | 32-34 | 35-37 | 38-42 |
| Частоты |  4
4
|  4
4
|   14
14
|   11
11
|  10
10
|  4
4
|  4
4
|
| модальный класс |
По вариационному ряду судят о развитии и распространении признака в данной группе. В крайних классах находится наименьшее число вариант, а в средних – наибольшее.
Графическое изображение вариационного ряда
Вариационный ряд можно представить в виде ступенчатой кривой, называемой гистограммой. Для этого на горизонтальной линии (оси абсцисс) наносят классы, а на вертикальной (ось ординат) – частоты. Основанием каждого столбика является соответствующее значение класса, а высота – число особей в нем. Если соединить прямыми линиями середины всех столбиков, получится вариационная кривая или полигон распределения. Полигон распределения должен своими ветвями касаться на оси абсцисс середины соседних классов.
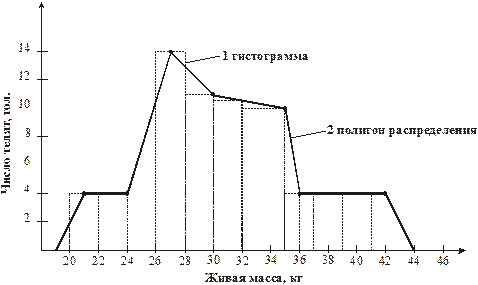
Рис. Распределение телят по живой массе при рождении.
1) – гистограмма; 2) – полигон распределения
При анализе графика можно видеть:
1. около середины вариационной кривой располагается наибольшее количество вариант;
2. распределение вариант по обе стороны от варианты вариационной кривой примерно симметрично;
3. число телят убывает к краям вариационного ряда. Вышеназванные закономерности характерны для большинства вариационных рядов. Для сравнения на одном графике нескольких распределений удобно пользоваться не гистограммой, а полигоном распределения.
Если взято малое количество животных, то в некоторых классах вариационного ряда варианты могут отсутствовать, тогда вариационная кривая бывает разорванной. При малом числе особей и растянутых вариационных рядах часто наблюдается двухвершинность или многовершинность. Если выборка взята достаточно большой, то двухвершинность указывает на смешение двух различных совокупностей (двух пород, линий и т.д.) или на выращивание и содержание животных в разных условиях и т.д.
Встречаются ассиметричные вариационные кривые со смещением вершин влево или вправо, т.е. положительная или отрицательная ассиметрия. Это объясняется неоднородностью условий развития животных данной совокупности, наличием в изучаемой группе большого количества особей с лучшими или худшими наследственными задатками, отбором. На нашем примере наблюдается небольшая отрицательная ассиметрия, т.е. вершина смещена влево. Если в средних классах вариационного ряда наблюдается преобладание вариант, то получается островершинная кривая, называемая эксцессом.
Дата добавления: 2021-05-18; просмотров: 273; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
