Вывод формулы Ньютона-Лейбница
Лекция . Определенный и несобственный интеграл
Понятие определенного интеграла и его свойства
Что такое определённый интеграл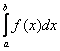 
?
Пусть функция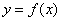 
определена на промежутке 
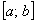. Для определённости и простоты считаем, что функция положительна 
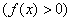и непрерывна на данном отрезке. Поставим задачу найти площадь 
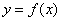криволинейной трапеции, ограниченной графиком функции , прямыми 
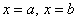и осью 
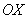. Обращаю внимание на тот факт, что непрерывность функции на отрезке заведомо гарантирует существование конечной площади .
Разобьём отрезок 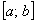на 
частей следующими точками:
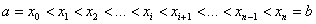(красные точки):
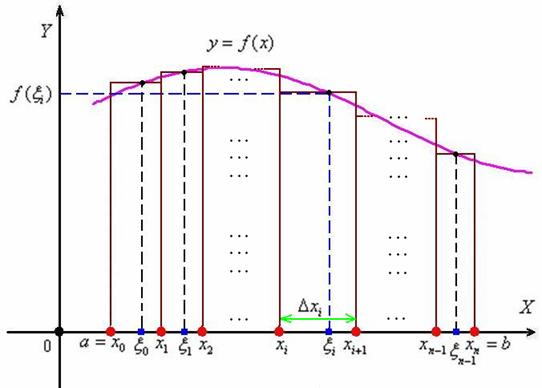
В результате получено частичных промежутков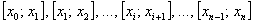 
с длинами 
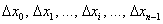соответственно. В общем случае длины различны – какие-то отрезки короче, какие-то длиннее. Максимальную длину называют диаметром разбиения и обозначают буквой «лямбда»: 
.
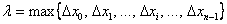Примечание: последняя запись читается, как «максимальное значение из множества (набора) 
»
В каждом из полученных промежутков опять же произвольно выбираем точки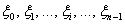 
(синие квадратики).
Примечание: 
(«кси») – 14-я буква греческого алфавита
Рассмотрим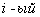 
промежуток 
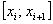. Его длина, очевидно, равна 
(зелёная обоюдоострая линия). Значению аргумента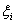 
соответствует значение функции 
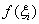(синие пунктирные линии), и произведение 
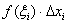в точности равно площади соответствующего коричневого прямоугольника.
Аналогично устроен каждый отрезок. Составим сумму, которая равна площади коричневой ступенчатой фигуры:
|
|
|
Данная сумма называется интегральной суммой, и её часто записывают в свёрнутом виде:
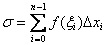
Примечание: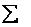 
– это значок суммы, а переменная 
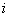– своеобразный «счётчик», т.е. сначала 
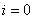, затем 
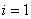, потом 
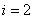, … и, наконец,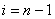 
Что означает прилагательное «интегральной»? В широком смысле слова, интегрировать – это значит, что-то объединять. В данном случае интегральная сумма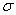 
объединяет площади коричневых прямоугольников и с некоторой точностью приближает площадь криволинейной трапеции: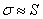 
Теперь зададимся вопросом: как улучшить точность приближения? Действия очевидны – увеличиваем и увеличиваем значение . При этом количество отрезков 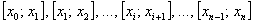растёт, а их длины 
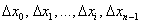– уменьшаются, в том числе неизбежно уменьшается и максимальная длина 
. Количество точек 
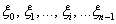тоже возрастает и ступенчатая фигура всё больше и больше напоминает криволинейную трапецию.
И, если количество отрезков разбиения устремить к бесконечности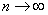 
, то интегральная сумма (площадь ступенчатой фигуры) будет стремиться к площади криволинейной трапеции: 
.
Таким образом, площадь криволинейной трапеции равна пределу интегральной суммы при диаметре разбиения, стремящемся к нулю:
Отметим:
1) В рассматриваемом контексте сумму 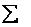ещё с 17 века обозначали растянутой буквой S (Summa). Это обозначение известно как значок интеграла:
|
|
|
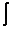
2) Если 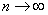(и, следовательно, 
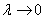), то значения 
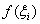стремятся «покрыть» все значения функции 
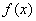из промежутка 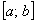, то есть:
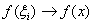, при этом пределы интегрирования: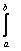 
3) И, наконец, длина любого промежуточного отрезка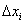 
становится бесконечно малой. Обозначение этой бесконечно малой длины мы тоже хорошо знаем, оно указывает, что объединение ведётся по переменной «икс»:
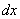
В результате, площадь криволинейной трапеции: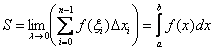 
Определение: конечный предел интегральной суммы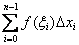 
при 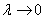, не зависящий ни от способа дробления отрезка 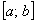, ни от выбора точек 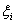, называется определённым интегралом функции 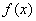по промежутку 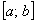и обозначается символом 
.
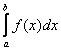При этом функция 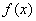называется интегрируемой в промежутке 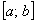. Для интегрируемости (а, значит, существования конечной площади), напоминаю, достаточно непрерывности функции на отрезке 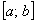. Если же на данном промежутке есть участки, где функция, например, не определена (нет её графика), то конечного предела 
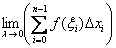и, соответственно, определённого интеграла 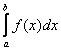не существует.
Формула Ньютона-Лейбница
Формулу 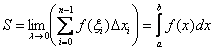очень трудно применить на практике (даже для простых функций), поэтому возникает задача отыскания более эффективного пути расчёта площади. И такой путь действительно существует – ведь из определения определённого интеграла следует, что он не зависит от способа разбиения промежутка 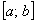и от выбора точек 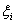. Важен лишь только нижний предел интегрирования «а», верхний предел интегрирования «бэ» и сама функция «эф от икс».
|
|
|
Вывод формулы Ньютона-Лейбница
Для нахождения определенного интеграла используют формулу Ньютона-Лейбница:
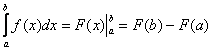, где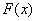 
– первообразная функция для функции .
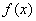Докажем ее.
Рассмотрим тот же график 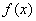и познакомимся с функцией переменной площади 
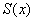. Что это за функция? Зафиксируем произвольную точку 
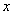(левая красная точка), лежащую между точками «а» и «бэ»:
В данной точке функция 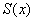равна площади криволинейной трапеции, которая расположена между зелёной и синей линиями и заштрихована синим цветом. Мысленно начните уменьшать значение «икс» и сдвигать синюю прямую влево – площадь 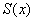начнёт уменьшаться и, в конце концов, в точке 
станет равной нулю: 
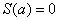(прямые совпадут). Теперь возвращаемся на исходную позицию и сдвигаем синюю линию вправо – в этом случае площадь 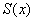начнёт расти. И когда мы достигнем верхнего предела 
(синяя прямая «закроет» красную), площадь будет равна в точности площади всей криволинейной трапеции: 
.
|
|
|
Таким образом, аргумент может изменяться в пределах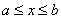 
, при этом функция 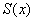(площадь) будет возрастать от 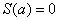до .
Докажем, что функция переменной площади 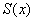является первообразной функцией для функции 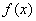, то есть докажем, что 
.
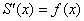Вернёмся к нашей точке «икс» и зададим в ней приращение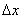 
(зелёная стрелка). Для определённости полагаем, что 
(случай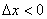 
доказывается аналогично). Приращение аргумента 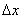влечёт приращение функции 
– геометрически это площадь криволинейной трапеции, которая заштрихована голубым цветом.
По так называемой теореме о среднем, на отрезке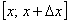 
существует точка «цэ» – такая, что площадь коричневого прямоугольника равна площади голубой трапеции:
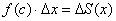
По определению производной, производная функции – это отношение приращения функции к приращению аргумента 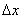при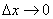 
:
.
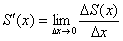И, ввиду равенства 
:
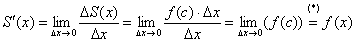
(*) Так как 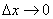, то точка «цэ» бесконечно близко приближается к точке «икс», и, соответственно: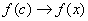 
Вспомним, что в предыдущей главе мы доказали, что площадь криволинейной трапеции – есть предел интегральной суммы: .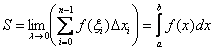
Но с другой стороны,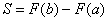 
.
И из этих двух фактов следует лаконичная формула Ньютона-Лейбница:
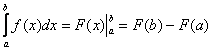, где 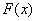– первообразная функция для функции .
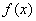Дата добавления: 2021-05-18; просмотров: 113; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!