Частные производные первого порядка. Полный дифференциал
Понятие функции двух и более переменных
Будем рассматривать функции двух переменных, так как все основные понятия и теоремы, сформулированные для функций двух переменных, легко обобщаются на случай большего числа переменных.
Пусть 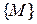 – множество упорядоченных пар действительных чисел
– множество упорядоченных пар действительных чисел 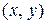 .
.
Определение. Если каждой упорядоченной паре чисел 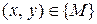 по некоторому закону
по некоторому закону 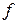 поставлено в соответствие единственное действительное число
поставлено в соответствие единственное действительное число 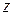 , то говорят, что задана функция двух переменных
, то говорят, что задана функция двух переменных 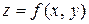 или
или  . Числа
. Числа 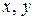 называются при этом независимыми переменными или аргументами функции, а число
называются при этом независимыми переменными или аргументами функции, а число 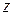 – зависимой переменной.
– зависимой переменной.
Пару чисел 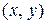 иногда называют точкой
иногда называют точкой  , а функцию двух переменных – функцией точки
, а функцию двух переменных – функцией точки 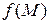 .
.
Значение функции 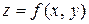 в точке
в точке 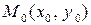 обозначают
обозначают 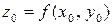 или
или 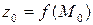 и называют частным значением функции двух переменных.
и называют частным значением функции двух переменных.
Совокупность всех точек  , в которых определена функция
, в которых определена функция 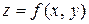 , называется областью определения этой функции. Для функции двух переменных область определения представляет собой всю координатную плоскость или ее часть, ограниченную одной или несколькими линиями.
, называется областью определения этой функции. Для функции двух переменных область определения представляет собой всю координатную плоскость или ее часть, ограниченную одной или несколькими линиями.
Например, область определения функции  – вся плоскость, а функции
– вся плоскость, а функции  – единичный круг с центром в начале координат (
– единичный круг с центром в начале координат ( 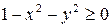 или
или 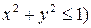 .
.

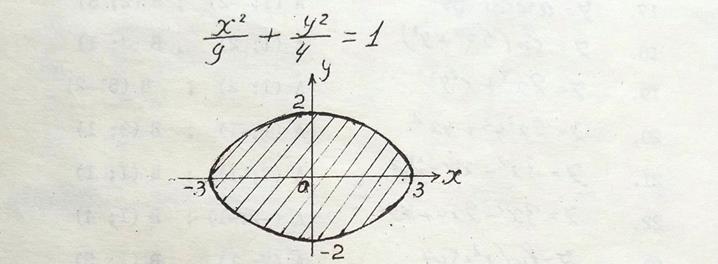
Предел и непрерывность функции двух переменных
Понятия предела и непрерывности функции двух переменных аналогичны случаю одной переменной.
Пусть 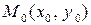 – произвольная точка плоскости.
– произвольная точка плоскости.  – окрестностью точки
– окрестностью точки 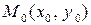 называется множество всех точек
называется множество всех точек  , координаты которых удовлетворяют неравенству
, координаты которых удовлетворяют неравенству 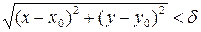 . Другими словами,
. Другими словами,  – окрестность точки
– окрестность точки 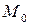 – это все внутренние точки круга с центром в точке
– это все внутренние точки круга с центром в точке 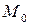 и радиусом
и радиусом  .
.
|
|
|
Определение. Число  называется пределом функции
называется пределом функции 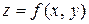 при
при  (или в точке
(или в точке 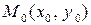 ), если для любого сколь угодно малого положительного числа
), если для любого сколь угодно малого положительного числа 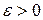 существует
существует 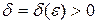 (зависящее от
(зависящее от 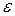 ) такое, что для всех
) такое, что для всех  и удовлетворяющих неравенству
и удовлетворяющих неравенству 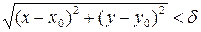 выполняется неравенство
выполняется неравенство  .
.
Обозначается предел следующим образом:
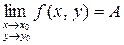 или
или  .
.

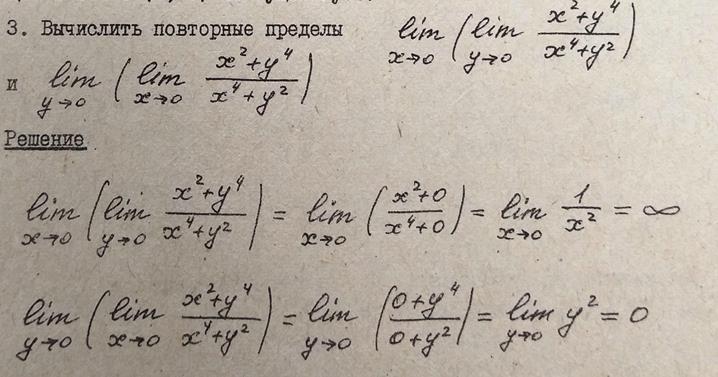
Пример. Найти предел  .
.
Решение. Введем обозначение 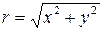 , откуда
, откуда 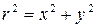 . При
. При  имеем, что
имеем, что 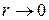 . Тогда
. Тогда
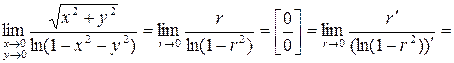
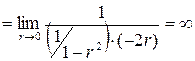 .
.

Определение. Функция 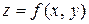 называется непрерывной в точке
называется непрерывной в точке 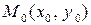 , если: 1)
, если: 1) 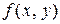 определена в точке
определена в точке 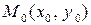 и ее окрестности; 2) имеет конечный предел
и ее окрестности; 2) имеет конечный предел 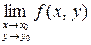 ; 3) этот предел равен значению функции в точке
; 3) этот предел равен значению функции в точке 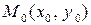 , т.е.
, т.е.  .
.
Функция 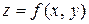 называется непрерывной в некоторой области, если она непрерывна в каждой точке этой области.
называется непрерывной в некоторой области, если она непрерывна в каждой точке этой области.
Точки, в которых условие непрерывности не выполняется, называются точками разрыва этой функции. В некоторых функциях точки разрыва образуют целые линии разрыва. Например, функция 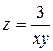 имеет две линии разрыва: ось
имеет две линии разрыва: ось 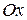 (
( 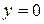 ) и ось
) и ось  (
(  ).
).
Пример. Найти точки разрыва функции 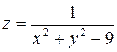 .
.
|
|
|
Решение. Данная функция не определена в тех точках, в которых знаменатель обращается в нуль, т. е. в точках, где 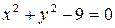 или
или 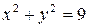 . Это окружность с центром в начале координат и радиусом
. Это окружность с центром в начале координат и радиусом 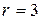 . Значит, линией разрыва исходной функции будет окружность
. Значит, линией разрыва исходной функции будет окружность 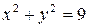 .
.
Частные производные первого порядка. Полный дифференциал
Пусть задана функция двух переменных 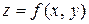 . Дадим аргументу
. Дадим аргументу 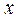 приращение
приращение 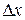 , а аргумент
, а аргумент  оставим неизменным. Тогда функция
оставим неизменным. Тогда функция 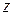 получит приращение
получит приращение 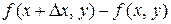 , которое называется частным приращением
, которое называется частным приращением 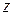 по переменной
по переменной 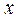 и обозначается
и обозначается 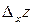 :
:  .
.
Аналогично, фиксируя аргумент 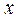 и придавая аргументу
и придавая аргументу  приращение
приращение 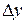 , получим частное приращение функции
, получим частное приращение функции 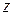 по переменной
по переменной  :
: 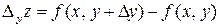 .
.
Величина 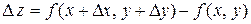 называется полным приращением функции
называется полным приращением функции 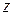 в точке
в точке  .
.
Определение. Частной производной функции двух переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению данной переменной, когда последнее стремится к нулю (если этот предел существует). Обозначается частная производная так: 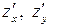 или
или 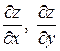 , или
, или 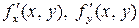 .
.
Таким образом, по определению имеем:
 ,
,
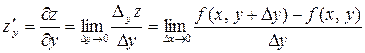 .
.
Частные производные функции 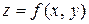 вычисляются по тем же правилам и формулам, что и функция одной переменной, при этом учитывается, что при дифференцировании по переменной
вычисляются по тем же правилам и формулам, что и функция одной переменной, при этом учитывается, что при дифференцировании по переменной 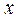 ,
,  считается постоянной, а при дифференцировании по переменной
считается постоянной, а при дифференцировании по переменной  постоянной считается
постоянной считается 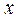 .
.
|
|
|
Пример. Найти частные производные функций:
а) 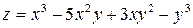 ;
;
Решение.
Чтобы найти  считаем
считаем  постоянной величиной и дифференцируем
постоянной величиной и дифференцируем 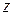 как функцию одной переменной
как функцию одной переменной 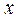 :
:
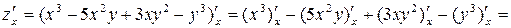
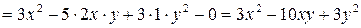 .
.
Аналогично, считая 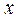 постоянной величиной, находим
постоянной величиной, находим 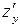 :
:
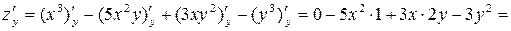
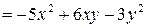 .
.

б) 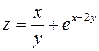 .
.
Решение.
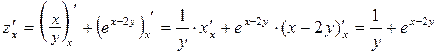 ;
;
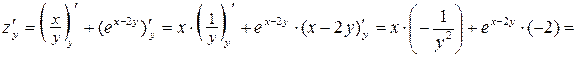
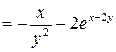 .
.
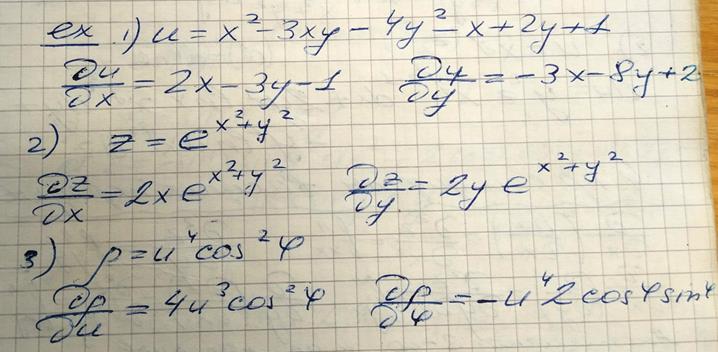



Определение. Полным дифференциалом функции 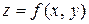 называется сумма произведений частных производных этой функции на приращения соответствующих независимых переменных, т.е.
называется сумма произведений частных производных этой функции на приращения соответствующих независимых переменных, т.е.  .
.

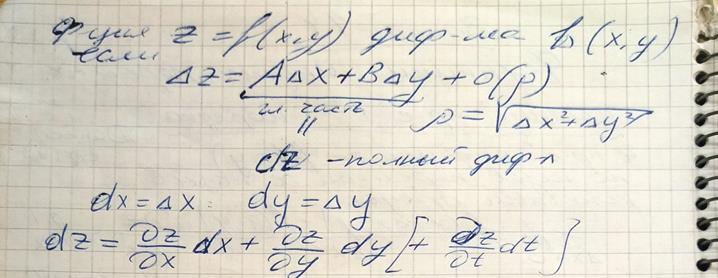
Учитывая, что дифференциалы независимых переменных совпадают с их приращениями, т.е. 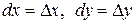 , формулу полного дифференциала можно записать в виде
, формулу полного дифференциала можно записать в виде
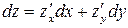 или
или 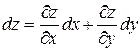 .
.
Пример. Найти полный дифференциал функции 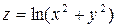 .
.
Решение. Так как 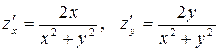 , то по формуле полного дифференциала находим
, то по формуле полного дифференциала находим 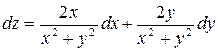 .
.
Дата добавления: 2021-04-05; просмотров: 68; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
