Числовые характеристики непрерывных случайных величин
Регрессия
Определение. Регрессией У на Х называется условное математическое ожидание У, при условии, что событие Х произошло, то есть
(6)
Регрессию У на Х можно рассматривать как функцию у(х). Рассмотрим как это происходит. Фиксируем, например, х1 и вычислим
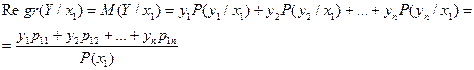 (7)
(7)
Аналогично вычисляется
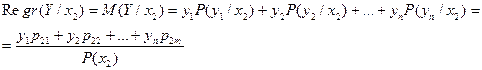 и т.д.
и т.д.
Отметим на плоскости (х;у) точки А1, А2 ,…, Ам с координатами (х1; 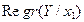 ),
),
(х2; 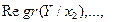 , (хм;
, (хм; 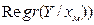 ). Соединим эти точки кривой, называемой кривой регрессии У на Х. Это график функции y(x).
). Соединим эти точки кривой, называемой кривой регрессии У на Х. Это график функции y(x).
Аналогично строится кривая регрессии Х на У, то есть график х=х(у).
Линейная регрессия
Имеем кривую регрессии У на Х. Это график функции y(x). Эта кривая проходит через центр тяжести, то есть через точку (М(Х); М(У)). Построим прямую у=кх+в, проходящую через точку (М(Х);М(У)), такую, что 
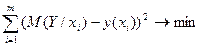 сумма квадратов расстояний от линии регрессии до этой прямой была наименьшей.
сумма квадратов расстояний от линии регрессии до этой прямой была наименьшей.
Уравнение линейной регрессии У на Х выглядит следующим образом:
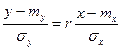 (8)
(8)
Построим теперь регрессию Х на У, то есть
Regr(X/Y)=M(X/Y). Это будет кривая х=х(у). Снова построим линейную регрессию Х на У, минимизируя квадраты расстояний, но уже по х, а не по у. Эта прямая также проходит через центр тяжести и имеет вид:
|
|
|
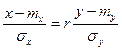 . (9)
. (9)
Чем меньше угол между прямыми, тем более жёсткая связь между Х и У. Если r=0, то прямые перпендикулярны. Одна горизонтальная, другая вертикальная. Случайные величины некоррелированные.
Функция распределения. Функция плотности распределения непрерывной случайной величины
Функцией распределения называют функцию 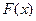 определяющую вероятность того, что случайная величина
определяющую вероятность того, что случайная величина 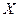 в результате испытания примет значение, меньшее
в результате испытания примет значение, меньшее 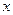 , т. е.
, т. е. 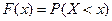 .
.
Пример 1. Дан ряд распределения случайной величины 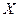 :
:
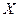
| –2 | 1 | 2 | 4 |
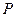
| 0,4 | 0,1 | 0,2 | 0,3 |
Составить функцию распределения 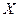 и построить ее график.
и построить ее график.
Решение:
при 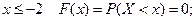
при 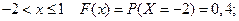
при 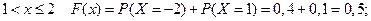
при 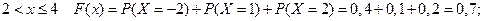
при 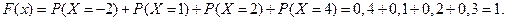
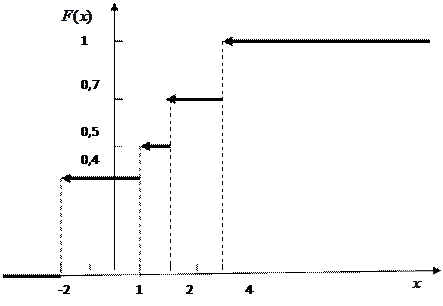
|
Рис. 1. График функции распределения
Вероятность того, что случайная величина примет значение, заключенное в интервале 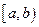 , равна приращению функции распределения на этом интервале:
, равна приращению функции распределения на этом интервале: 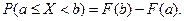
Для непрерывной случайной величины:
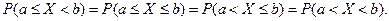
Пример 2. Случайная величина 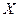 задана функцией распределения
задана функцией распределения
|
|
|
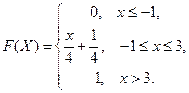
Равномерное распределение.
Найдите вероятность того, что в результате испытания 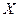 примет значение, принадлежащее интервалу
примет значение, принадлежащее интервалу 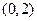 .
.
Решение. 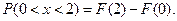 Так как на интервале
Так как на интервале 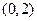
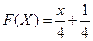 , то
, то 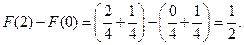 Следовательно,
Следовательно, 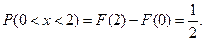
Плотностью распределения вероятностей непрерывной случайной величины 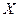 называют функцию
называют функцию 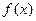 – первую производную от функции распределения
– первую производную от функции распределения 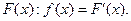
Свойства плотности распределения:
1. 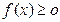 ;
;
2. Несобственный интеграл от плотности распределения в пределах
от 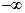 до
до 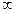 равен единице:
равен единице: 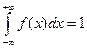 (основное условие нормировки).
(основное условие нормировки).
Пример 3. Дана функция распределения случайной величины 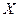 :
:
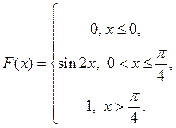
Найдите плотность распределения 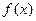 .
.
Решение. Плотность распределения равна первой производной от функции распределения:
распределения:
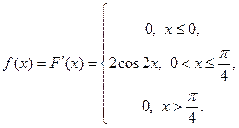
Вероятность того, что непрерывная случайная величина 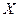 примет значение, принадлежащее интервалу
примет значение, принадлежащее интервалу 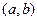 равна определенному интегралу от плотности распределения, взятому в пределах от
равна определенному интегралу от плотности распределения, взятому в пределах от 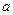 до
до 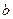 :
: 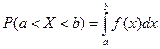 .
.
Пример 4. Задана плотность вероятности случайной величины 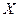
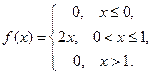
Найдите вероятность того, что в результате испытания X примет значение, принадлежащее интервалу 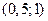 .
.
Решение. Искомая вероятность равна:
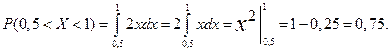
Зная плотность 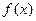 распределения можно найти функцию распределения по формуле
распределения можно найти функцию распределения по формуле 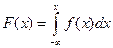 .
.
Пример 5 . Найдите функцию распределения 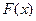 по данной плотности распределения:
по данной плотности распределения:
|
|
|
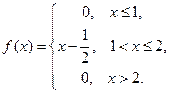
Решение. Используем формулу 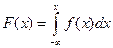 .
.
Если 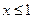 , то
, то 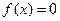 . Следовательно,
. Следовательно, 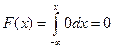 .
.
Если 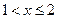 , то
, то 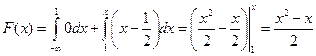 .
.
Если 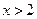 , то
, то 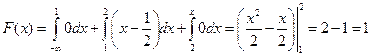 .
.
Итак, искомая функция распределения имеет вид:
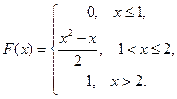
Несобственный интеграл от плотности распределения в пределах
от 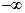 до
до 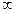 равен единице:
равен единице: 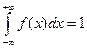 (основное условие нормировки).
(основное условие нормировки).
Пример 6 . Случайная величина задана плотностью распределения
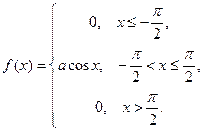
Найдите коэффициент 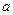 .
.
Решение. Воспользуемся формулой 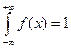 .
.
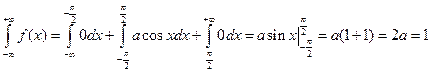 .
.
Следовательно, 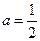 .
.
Числовые характеристики непрерывных случайных величин
Математическое ожидание непрерывной случайной величины 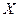 вычисляется по формуле:
вычисляется по формуле: 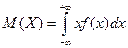 ; (10)
; (10)
дисперсия 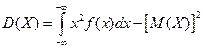 или (11)
или (11)

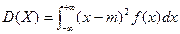 . (12)
. (12)
Пример 7. Найдите математическое ожидание, дисперсию, среднее квадратическое отклонение случайной величины 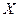 , заданной функцией распределения
, заданной функцией распределения 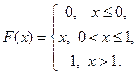
Решение. Найдем плотность распределения:
|
|
|
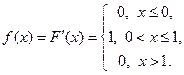
Математическое ожидание: 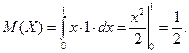
Среднее арифметическое.
Дисперсия 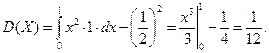
Следовательно, среднее квадратическое отклонение равно: 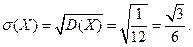
Пример 8. Плотность вероятности случайной величины имеет вид:
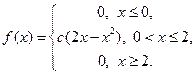
Найдите: 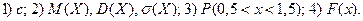
Решение. 1) По основному условию нормировки 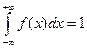 . Тогда получаем:
. Тогда получаем: 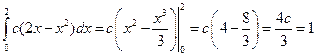 . Откуда
. Откуда 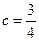 .
.
2) По формуле математического ожидания находим:
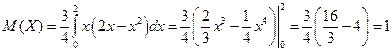 .
.
Дисперсия случайной величины равна: 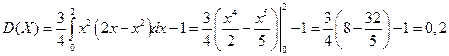 .
.
Следовательно, среднее квадратическое отклонение равно: 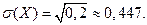
3) 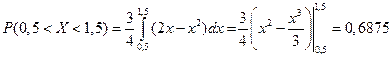 .
.
4) 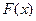 и
и 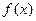 связаны формулой
связаны формулой 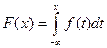 .
.
Поэтому, при 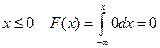 .
.
При 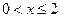
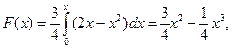
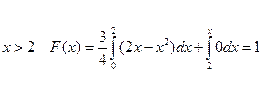 .
.
Следовательно, 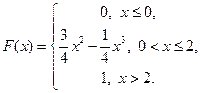
Дата добавления: 2021-05-18; просмотров: 43; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
