Замена переменной в определенном интеграле
Определенный интеграл, его свойства и вычисление.
Понятие определенного интеграла
Пусть функция y = f(x) определена на отрезке [a, b], a < b. Выполним следующие операции:
1) разобьем [a, b] точками a = x0 < x1 < ... < x i-1 < x i < ... < x n = b на n частичных отрезков [x0, x1], [x1, x2], ..., [x i-1, x i ], ..., [x n-1, x n ];
2) в каждом из частичных отрезков [x i-1, x i ], i = 1, 2, ... n, выберем произвольную точку и вычислим значение функции в этой точке: f(z i);
3) найдем произведения f(z i) · Δx i, где – длина частичного отрезка [x i-1, x i ], i = 1, 2, ... n;
4) составим интегральную сумму функции y = f(x) на отрезке [a, b]:
С геометрической точки зрения эта сумма σ представляет собой сумму площадей прямоугольников, основания которых – частичные отрезки [x0, x1], [x1, x2], ..., [x i-1, x i ], ..., [x n-1, x n ], а высоты равны f(z1), f(z2), ..., f(z n) соответственно (рис. 1). Обозначим через λ длину наибольшего частичного отрезка:
5) найдем предел интегральной суммы, когда λ → 0.
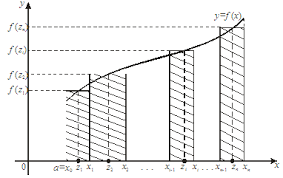
Рис. 1
Определение. Если существует конечный предел интегральной суммы (1) и он не зависит ни от способа разбиения отрезка [a, b] на частичные отрезки, ни от выбора точек z i в них, то этот предел называется определенным интегралом от функции y = f(x) на отрезке [a, b] и обозначается
Таким образом,
В этом случае функция f(x) называется интегрируемой на [a, b]. Числа a и b называются соответственно нижним и верхним пределами интегрирования, f(x) – подынтегральной функцией, f(x)dx – подынтегральным выражением, x – переменной интегрирования; отрезок [a, b] называется промежутком интегрирования.
|
|
|
Теорема 1. Если функция y = f(x) непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.
Определенный интеграл с одинаковыми пределами интегрирования равен нулю:
Если a > b, то, по определению, полагаем
Геометрический смысл определенного интеграла
Пусть на отрезке [a, b] задана непрерывная неотрицательная функция y = f(x). Криволинейной трапецией называется фигура, ограниченная сверху графиком функции y = f(x), снизу – осью Ох, слева и справа – прямыми x = a и x = b
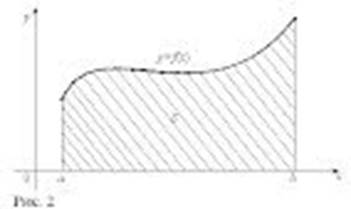
Определенный интеграл от неотрицательной функции y = f(x) с геометрической точки зрения равен площади криволинейной трапеции, ограниченной сверху графиком функции y = f(x), слева и справа – отрезками прямых x = a и x = b, снизу – отрезком оси Ох.
Основные свойства определенного интеграла
1.Значение определенного интеграла не зависит от обозначения переменной интегрирования:
2. Постоянный множитель можно выносить за знак определенного интеграла:
3. Определенный интеграл от алгебраической суммы двух функций равен алгебраической сумме определенных интегралов от этих функций:
|
|
|
4. Если функция y = f(x) интегрируема на [a, b] и a < b < c, то
5. (теорема о среднем). Если функция y = f(x) непрерывна на отрезке [a, b], то на этом отрезке существует точка , такая, что
Формула Ньютона–Лейбница
Теорема 2. Если функция y = f(x) непрерывна на отрезке [a, b] и F(x) – какая-либо ее первообразная на этом отрезке, то справедлива следующая формула:
,
которая называется формулой Ньютона–Лейбница. Разность F(b) - F(a) принято записывать следующим образом:
где символ называется знаком двойной подстановки.
Таким образом, формулу (2) можно записать в виде:
Пример 1. Вычислить интеграл
Решение. Для подынтегральной функции f(x) = x2 произвольная первообразная имеет вид
Так как в формуле Ньютона-Лейбница можно использовать любую первообразную, то для вычисления интеграла возьмем первообразную, имеющую наиболее простой вид:
Тогда
Замена переменной в определенном интеграле
Теорема 3. Пусть функция y = f(x) непрерывна на отрезке [a, b]. Если:
1) функция x = φ(t) и ее производная φ'(t) непрерывны при ;
2) множеством значений функции x = φ(t) при является отрезок [a, b];
3) φ(a) = a, φ(b) = b, то справедлива формула
|
|
|
которая называется формулой замены переменной в определенном интеграле.
В отличие от неопределенного интеграла, в данном случае нет необходимости возвращаться к исходной переменной интегрирования – достаточно лишь найти новые пределы интегрирования α и β (для этого надо решить относительно переменной t уравнения φ(t) = a и φ(t) = b).
Вместо подстановки x = φ(t) можно использовать подстановку t = g(x). В этом случае нахождение новых пределов интегрирования по переменной t упрощается: α = g(a), β = g(b).
Пример 2. Вычислить интеграл
Решение. Введем новую переменную по формуле . Возведя в квадрат обе части равенства , получим 1 + x = t2, откуда x = t2 - 1, dx = (t2 - 1)'dt = 2tdt. Находим новые пределы интегрирования. Для этого в формулу подставим старые пределы x = 3 и x = 8. Получим: , откуда t = 2 и α = 2; , откуда t = 3 и β = 3.
Дата добавления: 2021-05-18; просмотров: 60; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
