Нестационарное электрическое поле
Лекция ДО_4
ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ
В НЕСТАЦИОНАРНЫХ ЭЛЕКТРОМАГНИТНЫХ ПОЛЯХ
Нестационарное магнитное поле
Пусть теперь индукция магнитного поля B изменяется во времени.
Поскольку сила Лоренца всегда направлена перпендикулярно вектору B, магнитное поле не может передать энергию заряженной частице. Однако при изменении B во времени возникает вихревое электрическое поле Е:
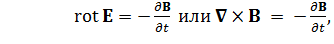 (1)
(1)
которое уже может ускорять частицы.
Рассмотрим этот процесс детальнее. Пусть l – элемент дуги вдоль траектории частицы, а 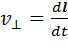 – ее поперечная скорость (скоростью vǁ в рамках нашего рассмотрения пренебрегаем!).
– ее поперечная скорость (скоростью vǁ в рамках нашего рассмотрения пренебрегаем!).
Запишем уравнение движения частицы в электромагнитных полях
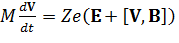 (2)
(2)
и умножим его левую и правую части скалярно на v^. Тогда, преобразовав его, получим:
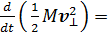
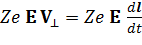 .
.
Интегрирование по периоду вращения позволяет вычислить изменение энергии частиц за 1 оборот:
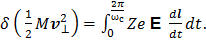 (3)
(3)
Если индукция магнитного поля меняется медленно (т.е. выполняется дрейфовое приближение), то интеграл по времени можно заменить интегралом вдоль невозмущенной орбиты
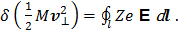 (4)
(4)
В этом выражении интеграл по замкнутому контуру по формуле Стокса можно заменить на поверхностный интеграл:
|
|
|
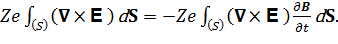 (5)
(5)
Здесь S -ориентированная поверхность, окруженная ларморовской орбитой. Направление нормали к ней определяется по правилу правой руки (пальцы указывают направление скорости V). Поскольку плазма является диамагнетиком, то для ионов произведение 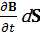 меньше нуля, а для электронов – больше нуля.
меньше нуля, а для электронов – больше нуля.
Т.к. зависимость B(t) считается слабой, будем считать, что за время одного оборота величина 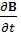 является постоянной и циклотронный радиус Rc также постоянен.
является постоянной и циклотронный радиус Rc также постоянен.
Тогда подставляя выражения для этих величин в формулу (5) и сокращая те же множители в числителе и знаменателе, получим:
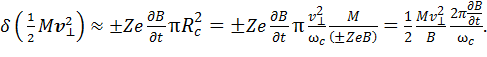
Но величина 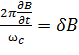 представляет собой изменение величины магнитной индукции за период вращения, а
представляет собой изменение величины магнитной индукции за период вращения, а 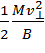 – магнитный момент µ.
– магнитный момент µ.
Таким образом, получаем
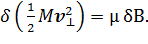 (6)
(6)
Поскольку левая часть этого равенства тождественно равна δ(μB), раскрывая приращение от произведения двух функций, придем к следующему соотношению:
|
|
|
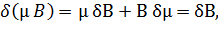 т.е.
т.е. 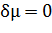 или
или
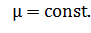 (7)
(7)
Таким образом, в медленно меняющемся магнитном поле магнитный момент остается постоянным.
При изменении индукции магнитного поля ларморовские орбиты сжимаются или расширяются, а поперечная энергия частиц уменьшается или увеличивается. Этот обмен энергией между магнитным полем и частицами очень просто описывается соотношением (7).
Инвариантность величины μ позволяет легко доказать следующую теорему:
Магнитный поток через поверхность, ограниченную ларморовской орбитой, постоянен.
Покажем это. Магнитный поток
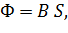 где
где 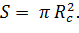
Подставляя сюда выражение для циклотронного радиуса, получим:
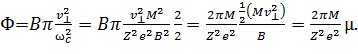 (8)
(8)
При этом в отличие от ситуации с постоянным по времени магнитным полем и ÑB ǁB параллельная скорость vǁ остается постоянной, а следовательно, в целом, энергия частицы меняется!
Нестационарное электрическое поле
Пусть теперь магнитное поле постоянно во времени, а поле E синусоидально меняется со временем с некоторой частотой ω.
|
|
|
Для определенности пусть вектор напряженности электрического поля E направлен по оси Ох:
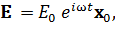 (9)
(9)
где x0 – орт в направлении Ox.
Дифференцируя записанное выражение, получим:
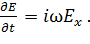 (9а)
(9а)
Учитывая, что вектор индукции магнитного поля направлен, как и ранее, по оси Оz, т.е. 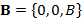 , уравнение движения заряженной частицы
, уравнение движения заряженной частицы
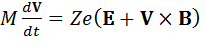 (10)
(10)
с учетом того, что векторное произведение представляется в виде определителя
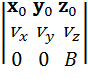 ,
,
можно записать в проекциях в следующем виде:
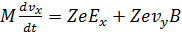 , (11)
, (11)
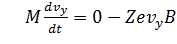 , (12)
, (12)
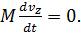 (13)
(13)
Если представить производные по времени как дифференцируемые величины с точкой сверху, первое уравнение (11) будет выглядеть так:
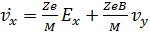 .
.
После дифференцирования по времени оно примет вид:
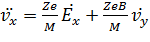 .
.
Подставляя в последнее уравнение значение производной по времени от проекции скорости v y из уравнения (12), получим:
|
|
|
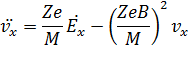
или, после умножения и деления второго слагаемого на B
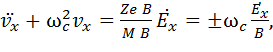 (14)
(14)
где ωc – циклотронная частота (как мы помним, всегда положительная величина!), а знаки ± учитывают сорт частицы (ион – электрон).
Аналогично тому, как было получено соотношение (14) относительно проекции v x, можно получить уравнение для проекции v y. Пожалуйста, сделайте это самостоятельно!!!!
Подставляя в уравнение (14) значение производной 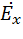 из (9а), запишем его в виде
из (9а), запишем его в виде
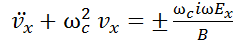 ,
,
откуда 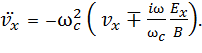 (15)
(15)
Аналогичную процедуру для получения выражения для 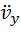 , п ожалуйста, сделайте самостоятельно.
, п ожалуйста, сделайте самостоятельно.
Введем обозначения
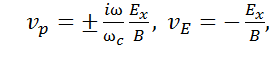 (16)
(16)
при этом верхний знак относится к частицам с положительным зарядом (ионам).
Тогда уравнения для вторых производных по времени от проекций скоростей примут вид:
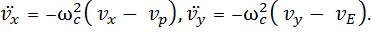 (17)
(17)
Как и ранее, в рамках дрейфового приближения для проекций скорости, перпендикулярной вектору индукции магнитного поля, будем искать решение в виде суперпозиции дрейфа и вращения v^:
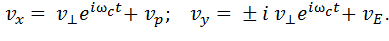 (18)
(18)
Если соотношения (18) дважды продифференцировать по времени и подставить в уравнения (17), получим следующее:
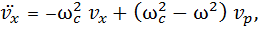 (19)
(19)
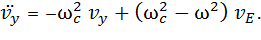 (20)
(20)
Последние уравнения совпадают с (17) только в том случае, когда ω2 мало по сравнению с 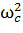 . Если теперь предположить, что напряженность электрического поля меняется медленно, т.е.
. Если теперь предположить, что напряженность электрического поля меняется медленно, т.е. 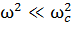 , то выражения (18) будут приближенными решениями уравнений (17).
, то выражения (18) будут приближенными решениями уравнений (17).
Из (18) следует, что движение ведущего центра в рассмотренном случае является более сложным, а его скорость имеет 2 составляющие:
а) y-компонента скорости, перпендикулярная векторам и напряженности электрического, и индукции магнитного поля – это обычный электрический дрейф в скрещенных электрическом и магнитном полях, за исключением лишь того, что vE теперь медленно осциллирует с частотой ω;
б) x-составляющая соответствует новому виду дрейфа вдоль направления E, который называется поляризационным дрейфом. Подумайте, пожалуйста, почему выбрано такое его название!
Заменяя в множителе перед мнимой частью формулы (16) 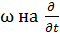 , можно обобщить это соотношение и записать скорость поляризационного дрейфа в виде:
, можно обобщить это соотношение и записать скорость поляризационного дрейфа в виде:
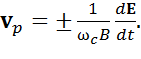 (21)
(21)
Поскольку скорости Vp у ионов и электронов направлены в разные стороны, возникает поляризационный ток. При Z = 1 его плотность составляет
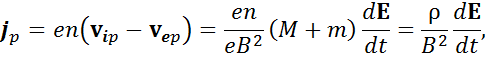
где ρ – массовая плотность плазмы.
Задание. Сформулируйте, для каких видов рассмотренных дрейфовых движений в плазме будут возникать дрейфовые токи, а для каких - нет. С чем это связано?
Рассмотрим далее другие виды дрейфа, не связанные с нестационарностью полей.
Гравитационный дрейф
В этом случае в качестве поперечной силы, приводящей к дрейфу, рассматривается сила тяжести F = M g. Выражение для скорости гравитационного дрейфа имеет вид:
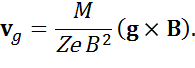
Ионы и электроны дрейфуют в различных направлениях, причем vge << vgi.
Плотность дрейфового тока в этом случае при Z = 1 составляет
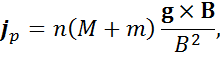
где M и m – массы иона и электрона соответственно.
Инерционный дрейф
В заключение рассмотрения дрейфового приближения для описания движения заряженных частиц в электромагнитных полях вернемся к ранее сформулированному парадоксу, связанному с пропорциональностью величине действующей силы не ускорения, а скорости дрейфа. Надеюсь, что вы уже думали об этой проблеме и имеете какое-то свое мнение на этот счет!
Если вы помните, при выводе формулы для скорости дрейфа мы предполагали ее постоянство во времени и опускали в уравнении движения слагаемое, содержащее производную по времени от скорости дрейфа. Давайте теперь в следующем приближении попробуем учесть это слагаемое и выяснить его влияние на результат и погрешность дрейфового приближения.
Для этого представим составляющую скорости частицы V^, перпендикулярную вектору индукции магнитного поля, в виде суммы не двух, а трех слагаемых, первое из которых представляет собой скорость быстрого вращения вокруг магнитной силовой линии, а два других характеризуют существенно более медленное смещение ведущего центра перпендикулярно вектору B, т.е. дрейфовое движение:
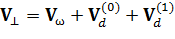 . (22)
. (22)
При этом 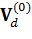 – та самая постоянная во времени скорость дрейфа, которую мы с вами исследовали в последних лекциях, а
– та самая постоянная во времени скорость дрейфа, которую мы с вами исследовали в последних лекциях, а 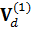 – некоторая поправка к ней в следующем приближении.
– некоторая поправка к ней в следующем приближении.
При подстановке последнего выражения в уравнение движения заряженной частицы
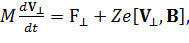 (23)
(23)
чтобы получить формулу для скорости дрейфа, мы пренебрегли 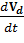 и получили выражение
и получили выражение
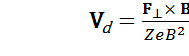 , (24)
, (24)
которое позволяет определить эту скорость 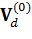 в нулевом приближении.
в нулевом приближении.
Для определения скорости дрейфа в первом приближении учтем слагаемое, содержащее производную от скорости дрейфа по времени. Подставив выражение (22) в уравнение движения (23), получим:
 (25)
(25)
Пренебрегая в этом выражении третьим слагаемым в левой части, которое содержит производную от скорости дрейфа в первом приближении по времени, отметим, что помеченные маркерами одного цвета слагаемые в левой и правой частях уравнения (25) тождественно равны друг другу. Так, из уравнения со слагаемыми только желтого цвета мы ранее определяли скорость вращения частицы вокруг магнитной силовой линии 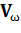 , а из уравнения только со слагаемыми голубого цвета – скорость дрейфа в нулевом приближении.
, а из уравнения только со слагаемыми голубого цвета – скорость дрейфа в нулевом приближении.
Оставшиеся слагаемые уравнения (25) дают нам возможность нахождения скорости дрейфа в следующем - первом – приближении (напоминаю, что слагаемым с производной по времени от скорости дрейфа в первом приближении – слагаемым, отмеченным красным маркером мы пренебрегаем!!!):
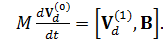 (26)
(26)
Искомая переменная 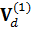 входит в уравнение (26) под знаком векторного произведения, поэтому для ее нахождения необходимо умножить обе части этого уравнения векторно на вектор индукции магнитного поля B и раскрыть тройное векторное произведение, как мы делали это при нахождении выражения для скорости дрейфа (24).
входит в уравнение (26) под знаком векторного произведения, поэтому для ее нахождения необходимо умножить обе части этого уравнения векторно на вектор индукции магнитного поля B и раскрыть тройное векторное произведение, как мы делали это при нахождении выражения для скорости дрейфа (24).
Не повторяя эти действия, приведу сразу ответ - выражение для скорости дрейфа в первом приближении:
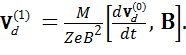 (27)
(27)
Отметим, что направление 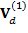 отличается от
отличается от 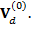
В соответствии с (27) выражением компоненту движения, определяемую скоростью 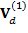 , можно рассматривать как дрейф под действием силы инерции
, можно рассматривать как дрейф под действием силы инерции 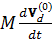 . (см. формулу (24)). Поэтому эта компонента получила название инерционного (инерциального) дрейфа. Рассмотрение этого вида дрейфа пригодится нам позже для анализа течения при генерации плазмы и заполнении ими магнитных ловушек.
. (см. формулу (24)). Поэтому эта компонента получила название инерционного (инерциального) дрейфа. Рассмотрение этого вида дрейфа пригодится нам позже для анализа течения при генерации плазмы и заполнении ими магнитных ловушек.
Подставив выражение для 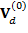 из (24), можно получить другую формулу для скорости дрейфа в первом приближении:
из (24), можно получить другую формулу для скорости дрейфа в первом приближении:
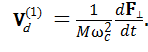 (28)
(28)
Т.к. в две последние формулы входят M и Z, частицы различных знаков заряда дрейфуют в различных направлениях и
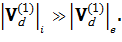
Аналогично приведенному рассмотрению можно найти поправки к скорости дрейфа и более высоких порядков малости. Для этого в уравнении (22) необходимо последовательно учитывать и другие слагаемые 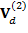 ,
, 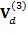 и т.д.
и т.д.
В заключение анализа движения независимых заряженных частиц обратим внимание, что дрейфовое приближение справедливо не для всех возможных электромагнитных конфигураций и не для всех параметров частиц и полей. Поэтому еще раз напоминаю условия его применимости!
Дата добавления: 2021-05-18; просмотров: 241; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
