Применение методов линейного программирования к решению матричных игр
Вычисление оптимальных стратегий
Соотношения превосходств и концепция доминирования
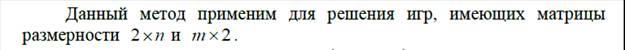
ПРИМЕР 2: Рассмотрим игру с матрицей
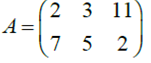
УКАЗАНИЕ:
ЦЕНА ИГРЫ В РАССМАТРИВАЕМОЙ ЗАДАЧЕ СООТВЕТСТВУЕТ ОРДИНАТЕ ВЕРХНЕЙ ТОЧКИ НИЖНЕЙ ОГИБАЮЩЕЙ ГРАФИКОВ ФУНКЦИЙ Y = M(x; j); j =1,2,...,n. ЭТО СПРАВЕДЛИВО ДЛЯ ИГР С МАТРИЦЕЙ 2´n.
ДЛЯ ИГР С МАТРИЦЕЙ m ´2 ГРАФИЧЕСКОЕ РЕШЕНИЕ АНАЛОГИЧНО, НО В ЭТОМ СЛУЧАЕ ЦЕНА ИГРЫ РАВНА ОРДИНАТЕ НИЖНЕЙ ТОЧКИ ВЕРХНЕЙ ОГИБАЮЩЕЙ ГРАФИКОВ ФУНКЦИЙ z = M (i; y);i =1,2,...,m.
Решение: Пусть игрок 1 применяет смешанную стратегию с вероятностями ( x,1- x) , а игрок 2 — чистую стратегию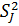 
. Обозначим математическое ожидание выигрыша игрока 1 в такой ситуации через M ( x; j) , где j -номер стратегии игрока 2. Тогда математическое ожидание выигрыша для игрока 1, если игрок 2 применяет чистую стратегию 
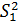, будет равно:
M( x;1)=2 x+ 7(1- x)= 7-5x.
Аналогично, если игрок 2 применяет чистую стратегию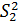 
, то:
M( x;2)=3 x+5(1- x)= 5-2x,
а если игрок 2 применяет чистую стратегию 
, то
M( x;3)=11x+2(1- x)= 2+ 9 x .
Дадим графическую интерпретацию решения. На плоскости введем ортогональную систему координат. По оси абсцисс отложим вероятность x. Тогда точки x =0 и x =1 соответствуют тому, что игрок 1 выберет чистые стратеги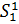и 
и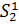 
соответственно. По оси ординат отложим выигрыш игрока 1, равный M ( x; j) и проведем три прямые
y=7-5x
y=5-2x
y=2+ 9 x, при xÎ[0,1]
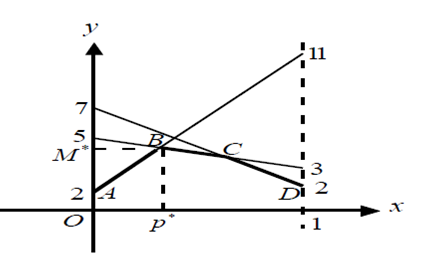
Рассуждения: Минимальное значение y при данном значении x соответствует выигрышу игрока 1 при выборе игроком 2 чистых стратегий 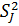при j=1,2,3 соответственно. То есть при каждом выборе игроком 1 стратегии x он может быть уверен в том, что получит, по крайней мере, выигрыш, соответствующий наименьшей из ординат точек построенных графиков.
|
|
|
Точки, удовлетворяющие такому условию, образуют ломаную ABCD , которую будем называть нижней огибающей трех построенных графиков функций. Таким образом, для игрока 1 выбрать оптимальное x ,значит, выбрать такое x , при котором ордината точки нижней огибающей будет наибольшей, то есть СЛЕДУЕТ НАЙТИ ВЕРХНЮЮ ТОЧКУ НИЖНЕЙ ОГИБАЮЩЕЙ.
Для точного нахождения x=p(абсцисса этой точки) и M(мат. ожидание) необходимо решить систему уравнений:
Решая эту систему получим y=49/11, x=3/11.
Тогда (1- x) = 8/11.
Вывод: Таким образом оптимальная стратегия игрока 1 есть вектор (3/11,8/11) ,
а цена игры при этом равна V =49/11.
Из рисунка видно, что стратегия 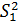в оптимальном решении не участвует, значит оптимальное решение для игрока 2 можно найти из приведенной матрицы вида
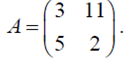
Решение легко определить графическим методом: пусть игрок 2 применяет смешанную стратегию ( y,1- y) , а игрок 1 выбирает чистые стратеги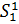и и .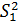
|
|
|
Обозначим математическое ожидание выигрыша игрока 2 через M(i; y) , где i - номер стратегии игрока 1.
Тогда имеем:
M( 1;y)=3y+ 11(1- y)= 11-8y.
M( 2;y)=5 y+2(1- y)= 2-3y,
Чертим графики:
z=11-8y
z=2-3y
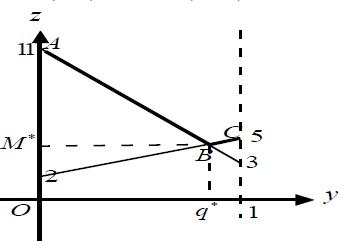
Находим точку пересечения графиков, решаем систему уравнений
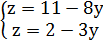
Решение системы: z=q*=49/11, x=M*=9/11.
Таким образом, оптимальная стратегия игрока 2 задается вектором (0 , 9/11 ,2/11) при цене игры V= 49/11.
Пример 2: Пусть задана платежная матрица
Пусть игрок 1 применяет смешанную стратегию (x, 1- x), а игрок 2 – чистые стратегии, тогда проделывая все, как в примере выше получим:
Тогда математическое ожидание выигрыша для игрока 1, если игрок 2 применяет чистую стратегию 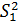, будет равно:
M( x;1)=2 x+ 7(1- x)= 7-5x.
Аналогично, если игрок 2 применяет чистую стратегию 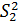, то:
M( x;2)=4x+4(1- x)= 4,
а если игрок 2 применяет чистую стратегию , то
M( x;3)=11x+2(1- x)= 2+ 9 x .
Чертим график. НУЖНО ПРОСЧИТЫВАТЬ ПРИ ПОСТРОЕНИИ ДВЕ ТОЧКИ Х=0 И Х=1 ДЛЯ КАЖДОГО ГРАФИКА:
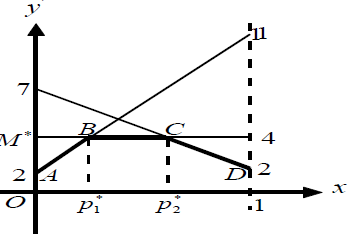
Решим совместно второе и третье, а также второе и первое уравнения:
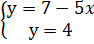и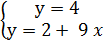 
Из первого x= p 2* =3/5, из второго x= p 1* =2/9. V = M *=4
Значит, оптимальной для игрока 1 является любая стратегия (x,1- x) , где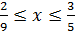 
, при этом цена игры V= 4 . Оптимальная стратегия для игрока 2 в этой игре равна (0,1,0)
|
|
|
Применение методов линейного программирования к решению матричных игр
прибавим ко всем элементам матрицы 2 A число k = 6. Получим матрицу
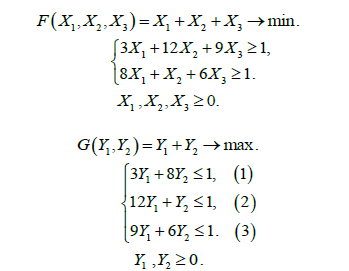
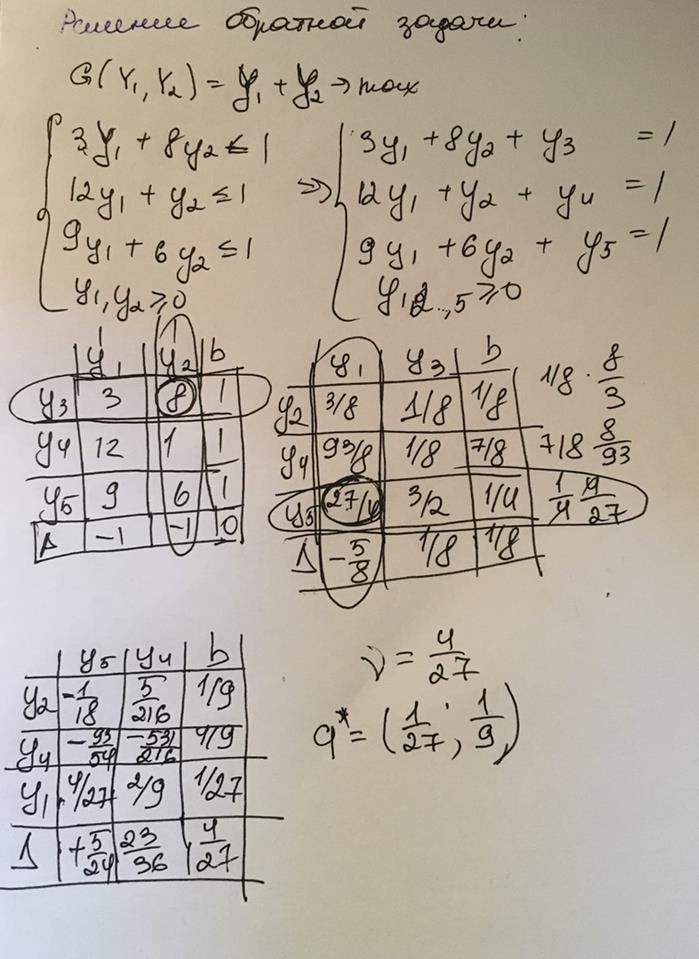
Задача (1) является двойственной к задаче (2). Для нахождения оптимального плана задачи (1) воспользуемся одной из теорем двойственности. Так как на оптимальном плане задачи (2) второе ограничение выполняется в виде строгого неравенства, оптимальное значение соответствующей ему двойственной переменной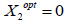 
. При этом, так как, то оба ограничения задачи (1) выполняются на оптимальном плане в виде равенств 
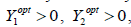. Таким образом, для того, чтобы найти оптимальные значения переменных и , следует решить систему линейных уравнений:
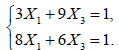
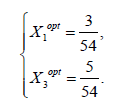
Цена игры и оптимальные стратегии игроков (1) и (2) в игре с платежной матрицей A
Дата добавления: 2021-05-18; просмотров: 70; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!