ЗАДАНИЯ РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ
РАСЧЕТНО-ГРАФИЧЕСКАЯ
РАБОТА
КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ
ИНТЕГРАЛЫ
ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ
КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
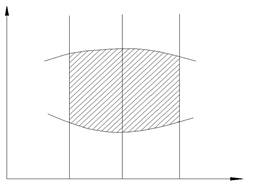
1. Двойной интеграл в декартовых координатах
|
|
|
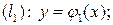
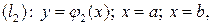 причем
причем 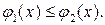
|
 пересекают границы области D не более, чем в двух точках. Тогда
пересекают границы области D не более, чем в двух точках. Тогда
|
|
|
|
|
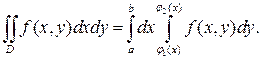
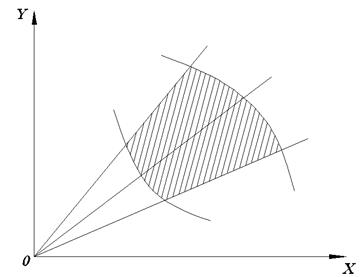
2. Двойной интеграл в полярных координатах
|
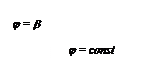 | ||||||||
| ||||||||
| ||||||||
| ||||||||
Область D ограничена линиями: 
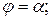
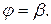 Тогда
Тогда

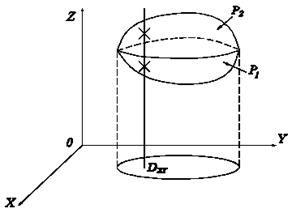
3. Объем тела двойным интегралом
|
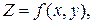 с боков – цилиндрической поверхностью с образующими параллельными оси OZ, снизу – плоской областью D. Тогда
с боков – цилиндрической поверхностью с образующими параллельными оси OZ, снизу – плоской областью D. Тогда

Площадь плоской области D находится по формуле

4. Объем тела тройным интегралом
|
 причем
причем 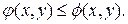
|
|
|
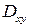 - проекция тела в плоскость x 0 y.
- проекция тела в плоскость x 0 y.
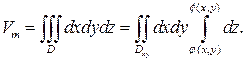
5. Пусть 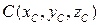 – центр тяжести тела D. Тогда:
– центр тяжести тела D. Тогда: 
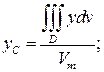
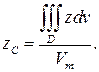 Здесь плотность
Здесь плотность 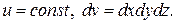
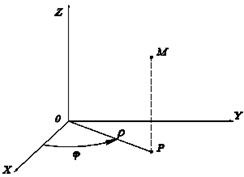
6. Цилиндрические координаты:
|
 - в декартовых координатах;
- в декартовых координатах;
2) эта же точка 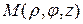 - в цилиндрических координатах, где
- в цилиндрических координатах, где  - угол
- угол 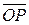 с осью OX, Z=PM (как в декартовых координатах).
с осью OX, Z=PM (как в декартовых координатах).
Тогда
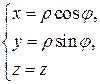
и

7. Криволинейный интеграл (по координатам)

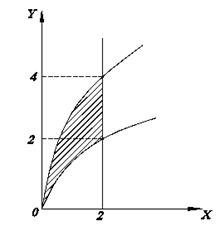
где AB – плоская кривая, соединяющая точки A и B.
Если AB задана так:  т.е.
т.е.
|
то
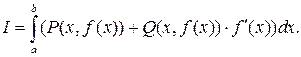
Работа переменной силы 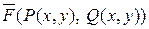 на пути AB находится по формуле
на пути AB находится по формуле
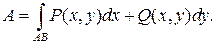
Площадь плоской области, ограниченной замкнутой кривой l, находится по формуле

8. Условие полного дифференциала:
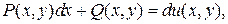 если
если 
Для восстановления 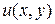 используются формулы:
используются формулы:

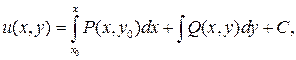 где
где  – точка непрерывности
– точка непрерывности 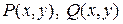 и их частных производных.
и их частных производных.
ОБРАЗЕЦ ВЫПОЛНЕНИЯ РГР
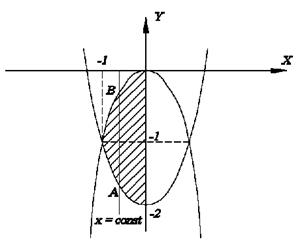
№ 1. Изменить порядок интегрирования:

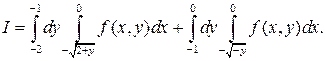
Решение:
Повторный интеграл является следствием двойного, поэтому 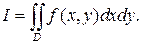
Для восстановления области D выписываем из данного повторного интеграла границы области:

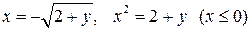 - уравнение параболы с вершиной в точке (0, -2).
- уравнение параболы с вершиной в точке (0, -2).
|
|
|
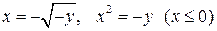 - уравнение параболы с вершиной в точке (0, 0).
- уравнение параболы с вершиной в точке (0, 0).
Найдем точки пересечения парабол:
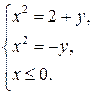
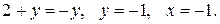
По данному повторному интегралу I восстанавливаем вид области D:
|
Производим переход в двойном интеграле к повторному, при этом внешнее интегрирование производим по x, внутреннее – по y.
Получим 
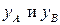 находим из уравнений соответствующих парабол:
находим из уравнений соответствующих парабол:
1) точка A лежит на параболе 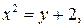 значит,
значит, 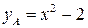 ;
;
2) точка B лежит на параболе 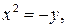 значит,
значит, 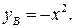
Окончательно получим: 
Ответ: 
№ 2. С помощью двойного интеграла вычислить площадь фигуры, ограниченной данными линиями (сделать чертеж):
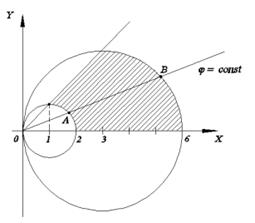 |
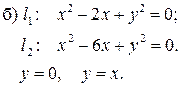
Решение:
Преобразуем данные уравнения
окружностей:
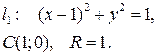
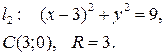
Переводим уравнения окружностей в полярные координаты, используя формулы: 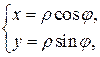 тогда
тогда 

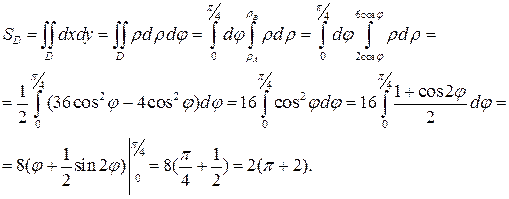
Ответ: 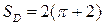 (кв. ед.).
(кв. ед.).
№ 3. Найти объем тела, ограниченного заданными поверхностями (сделать схематический чертеж): 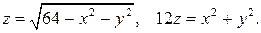
Решение:
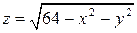 - уравнение сферы - C(0, 0), R=8, z³0.
- уравнение сферы - C(0, 0), R=8, z³0.
 - уравнение параболоида вращения.
- уравнение параболоида вращения.
Найдем точки пересечения поверхностей:
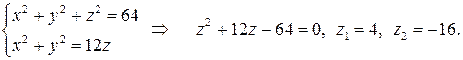
|
Переводим уравнения данных поверхностей в цилиндрические координаты, используя формулы:
|
|
|

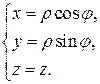
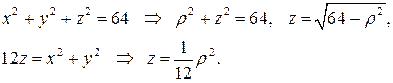
Тогда:

где 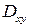 - проекция тела D в плоскость xoy.
- проекция тела D в плоскость xoy.
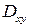 - есть круг, ограниченный окружностью
- есть круг, ограниченный окружностью 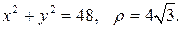
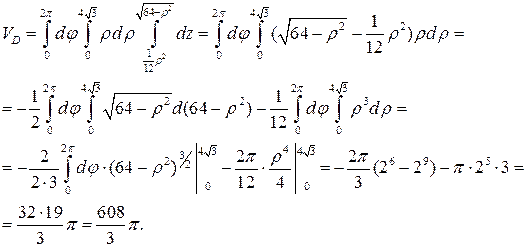
Ответ: 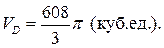
№ 4. а) Тело D задано ограничивающими его поверхностями, m – плотность. Найти массу тела (сделать чертеж проекции тела в плоскость xoy):
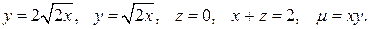
Решение:
|
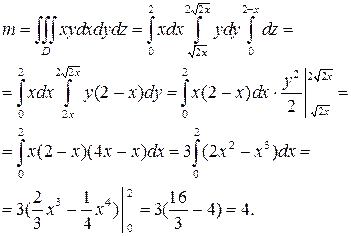
Ответ: m=4.
б) Найти центр тяжести тела, заданного ограничивающими его поверхностями (сделать чертеж проекции тела в плоскость  ):
):

Решение:

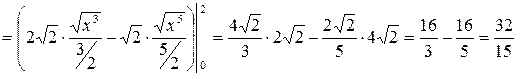 .
.
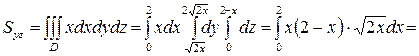
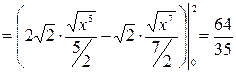 .
.
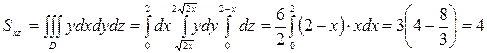 .
.
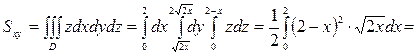
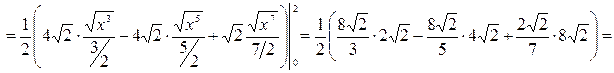
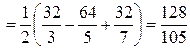 .
.
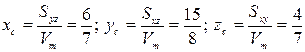
Ответ: 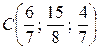 .
.
№ 5. Проверить, что данное выражение является полным дифференциалом и восстановить  с помощью криволинейного интеграла. Сделать проверку.
с помощью криволинейного интеграла. Сделать проверку.
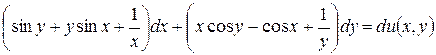 .
.
Решение:
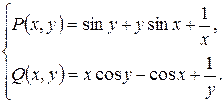
 .
.
Так как 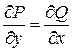 , то данное выражение является полным дифференциалом.
, то данное выражение является полным дифференциалом.
Пусть  .
.
Пусть 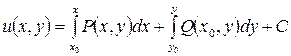 .
.
Тогда
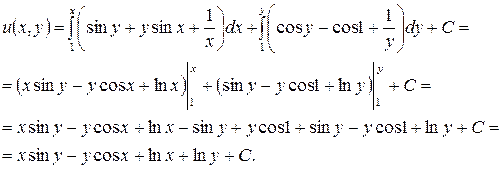
Проверка:
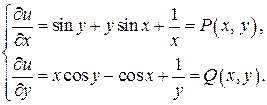
ЗАДАНИЯ РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ
1. Изменить порядок интегрирования (сделать чертеж области):
1.1. 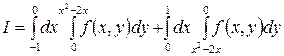 .
.
1.2.  .
.
1.3. 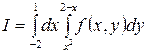 .
.
1.4. 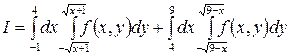 .
.
1.5. 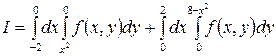 .
.
1.6.  .
.
1.7. 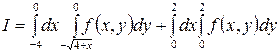 .
.
1.8. 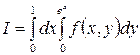 .
.
1.9. 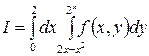 .
.
1.10.  .
.
1.11. 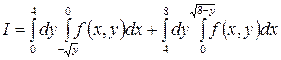 .
.
1.12.  .
.
1.13. 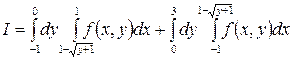 .
.
1.14.  .
.
1.15. 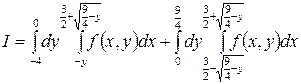 .
.
1.16.  .
.
1.17.  .
.
1.18. 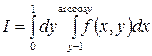 .
.
1.19. 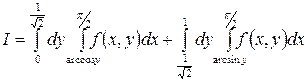 .
.
1.20.  .
.
2. С помощью двойного интеграла найти площадь фигуры, ограниченной данными линиями (сделать чертеж):
2.1. 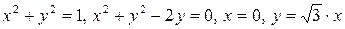 .
.
2.2.  .
.
2.3. 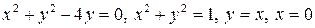 .
.
2.4. 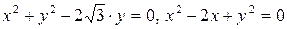 .
.
2.5.  .
.
|
|
|
2.6.  .
.
2.7.  .
.
2.8.  .
.
2.9. 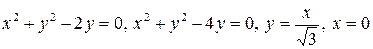 .
.
2.10. 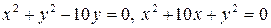 .
.
2.11. 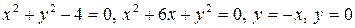 .
.
2.12. 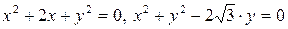 .
.
2.13. 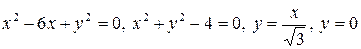 .
.
2.14. 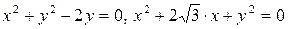 .
.
2.15. 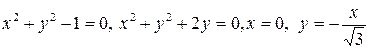 .
.
2.16.  .
.
2.17. 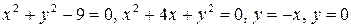 .
.
2.18. 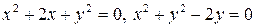 .
.
2.19.  .
.
2.20. 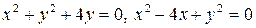 .
.
3. Найти объем тела, ограниченного заданными поверхностями (сделать схематический чертеж):
3.1. 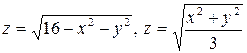 . 3.2.
. 3.2. 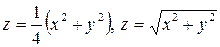 .
.
3.3. 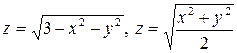 . 3.4.
. 3.4.  .
.
3.5. 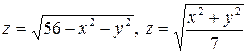 . 3.6.
. 3.6.  .
.
3.7.  . 3.8.
. 3.8. 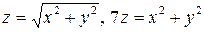 .
.
3.9.  . 3.10.
. 3.10. 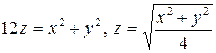 .
.
3.11.  . 3.12.
. 3.12. 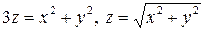 .
.
3.13. 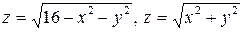 . 3.14.
. 3.14. 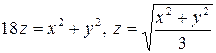 .
.
3.15. 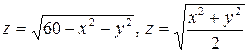 . 3.16.
. 3.16.  .
.
3.17. 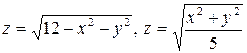 . 3.18.
. 3.18. 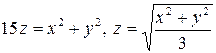 .
.
3.19. 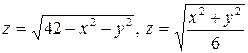 . 3.20.
. 3.20. 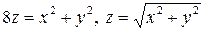 .
.
4. Тело задано ограничивающими его поверхностями, плотность u = const. Найти центр тяжести тела (сделать чертеж проекции тела в плоскость xoy):
4.1.  .
.
4.2.  .
.
4.3. 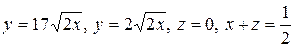 .
.
4.4. 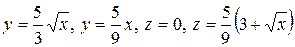 .
.
4.5. 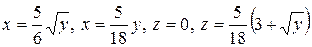 .
.
4.6.  .
.
4.7. 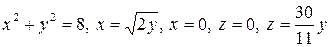 .
.
4.8. 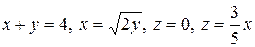 .
.
4.9. 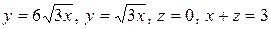 .
.
4.10. 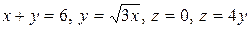 .
.
4.11.  .
.
4.12.  .
.
4.13. 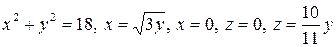 .
.
4.14.  .
.
4.15. 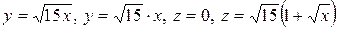 .
.
4.16. 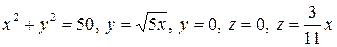 .
.
4.17. 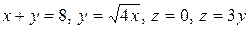 .
.
4.18. 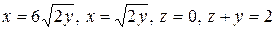 .
.
4.19. 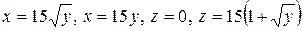 .
.
4.20. 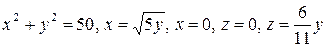 .
.
5. Проверить, что данное выражение является полным дифференциалом и восстановить  с помощью криволинейного интеграла. Сделать проверку:
с помощью криволинейного интеграла. Сделать проверку:
5.1.  .
.
5.2. 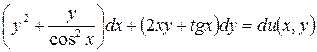 .
.
5.3.  .
.
5.4. 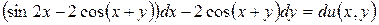 .
.
5.5. 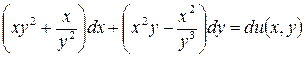 .
.
5.6.  .
.
5.7. 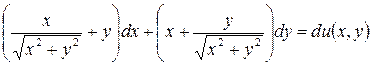 .
.
5.8.  .
.
5.9. 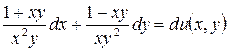 .
.
5.10. 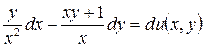 .
.
5.11. 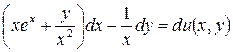 .
.
5.12.  .
.
5.13. 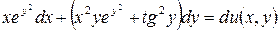 .
.
5.14. 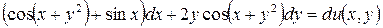 .
.
5.15. 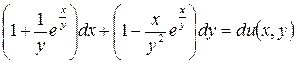 .
.
5.16.  .
.
5.17. 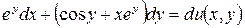 .
.
5.18. 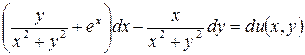 .
.
5.19.  .
.
5.20.  .
.
Дата добавления: 2021-05-18; просмотров: 59; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!