Эпюры поперечных сил и изгибающих моментов
Глава 23
ИЗГИБ
Понятие о чистом изгибе прямого бруса
 Чистым изгибом называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только изгибающий момент Деформация чистого изгиба будет, например, иметь место, если к прямому брусу в плоскости, проходящей через ось, приложить две равные по величине и противоположные по знаку пары сил.
Чистым изгибом называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только изгибающий момент Деформация чистого изгиба будет, например, иметь место, если к прямому брусу в плоскости, проходящей через ось, приложить две равные по величине и противоположные по знаку пары сил.
На изгиб работают балки, оси,
валы и другие детали конструкций (определение балки известно из теоретической механики). В дальнейшем почти всегда мы будем рассматривать такие брусья, у которых имеется по крайней мере одна плоскость симметрии и плоскость действия нагрузок совпадает с ней. В этом случае деформация изгиба происходит в плоскости действия внешних сил и изгиб называется прямым в отличие от косого изгиба, рассматриваемого в подразд. 23.9.
При изучении деформации изгиба будем мысленно представлять себе, что балка состоит из бесчисленного количества волокон, параллельных оси. Для того чтобы получить представление о деформации изгиба, проведем два опыта.
 Балку, свободно лежащую на двух опорах, в верхней и нижней,
Балку, свободно лежащую на двух опорах, в верхней и нижней,
частях которой предварительно сделаны пазы и в них помещены
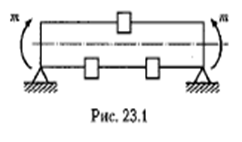
точно пригнанные по размеру пазов бруски, подвергнем деформации изгиба (рис. 23.1). В результате этого бруски, расположенные
на выпуклой стороне, выпадут из пазов, а бруски, расположенные
на вогнутой стороне, будут зажаты.
|
|
|
На боковую поверхность призматического резинового (для
большей наглядности) бруса прямоугольного сечения нанесем сетку продольных и поперечных прямых линий и подвергнем этот
брус деформации чистого изгиба (рис. 23.2). В результате можно
видеть следующее:
а)поперечные прямые линии
останутся при деформации прямыми, но повернутся навстречу друг к другу;
б)продольные прямые линии,
а также ось бруса искривятся;
в)сечения бруса расширятся
в поперечном направлении на вогнутой стороне и сузятся на выпуклой стороне.
Из этих опытов можно сделать вывод, что при чистом изгибе справедлива гипотеза плоских сечений; волокна, лежащие на выпуклой стороне, растягиваются, лежащие на вогнутой стороне — сжимаются, а на границе между ними лежит нейтральный слои волокон, которые только искривляются, не изменяя своей длины.
Полагая справедливой гипотезу о не надавливании волокон, можно утверждать, что при чистом изгибе в поперечном сечении бруса возникают только нормальные напряжения растяжения и сжатия, неравномерно распределенные по сечению.
Искривление волокон и оси бруса происходит за счет неравномерного распределения нормальных напряжений по поперечному сечению.
|
|
|
Линия пересечения нейтрального слоя с плоскостью поперечного сечения называется нейтральной осью (и.о.). На нейтральной оси нормальные напряжения равны нулю.
23.2. Изгибающий момент и поперечная сила
Как известно из теоретической механики, опорные реакции балок определяют, составляя и решая уравнения равновесия статики для всей балки. Будем помнить, что при определении внутренних сил реакции связей учитываются наравне с активными внешними силами, действующими на балку.
Для определения внутренних силовых факторов применим метод сечений, причем изображать балку будем только одной линией — осью, к которой приложены активные и реактивные силы. Рассмотрим два случая.
1. К балке приложены две равные и противоположные по знаку пары сил (рис. 23.3).
Рассматривая равновесие части балки, расположенной слева или справа от сечения 1—1, видим, что во всех поперечных сечениях возникает только изгибающий момент Ми, равный внешнему моменту. Таким образом, это случай чистого изгиба.
Изгибающий момент есть результирующий момент относительно нейтральной оси внутренних нормальных сил, действующих в поперечном сечении балки.
|
|
|
Обратим внимание на то, что изгибающий момент имеет разное направление для левой и правой частей балки. Это говорит о непригодности правила знаков статики при определении знака изгибающего момента.
2. К балке приложены активные и реактивные силы, перпендикулярные оси (рис. 23.4).

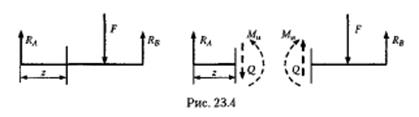
Рассматривая равновесие частей балки, расположенных слева и справа, видим, что в поперечных сечениях должны действовать изгибающий момент Ми и поперечная сила Q . Из этого следует, что в рассматриваемом случае в точках поперечных сечений действуют не только нормальные напряжения, соответствующие изгибающему моменту, но и касательные, соответствующие поперечной силе.
Поперечная сила есть равнодействующая внутренних касательных сил в поперечном сечении балки.
Обратим внимание на то, что поперечная сила имеет противоположное направление для левой и правой частей балки, что говорит о непригодности правила знаков статики при определении знака поперечной силы.
Изгиб, при котором в поперечном сечении балки действуют изгибающий момент и поперечная сила, называется поперечным.
В общем, случае при поперечном изгибе изгибающий момент и поперечная сила в разных сечениях могут иметь неодинаковое значение.
|
|
|
У балки, находящейся в равновесии под действием плоской системы сил, алгебраическая сумма моментов всех активных и реактивных сил относительно любой точки равна нулю; следовательно, сумма моментов внешних сил, действующих на балку левее сечения, численно равна сумме моментов всех внешних сил, действующих на балку правее сечения.
Таким образом, изгибающий момент в сечении балки численно равен алгебраической сумме моментов относительно центра тяже сти сечения всех внешних сил, действующих справа или слева от се чения.
У балки, находящейся в равновесии под действием плоской системы сил, перпендикулярных оси (т.е. системы параллельных сил), алгебраическая сумма всех внешних сил равна нулю; следовательно, сумма внешних сил, действующих на балку левее сечения, численно равна сумме сил, действующих на балку правее сечения.
Таким образом, поперечная сила в сечении балки численно равна алгебраической сумме всех внешних сил, действующих справа или слева от сечения.
Так как правила знаков статики неприемлемы для установления знаков изгибающего момента и поперечной силы, установим для них другие правила знаков, а именно:
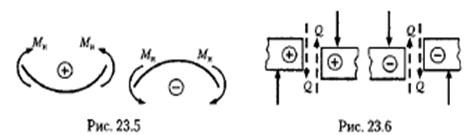
если внешняя нагрузка стремится изогнуть балку выпуклостью вниз, то изгибающий момент в сечении считается положительным, и наоборот, если внешняя нагрузка стремится изогнуть балку выпуклостью вверх, то изгибающий момент в сечении считается от рицательным (рис. 23.5);
если сумма внешних сил, лежащих по левую сторону от сечения, дает равнодействующую, направленную вверх, то поперечная сила в сечении считается положительной, если равнодействующая направлена вниз, то поперечная сила в сечении считается отрицательной; для части балки, расположенной справа от сечения, знаки поперечной силы будут противоположными (рис. 23.6).
Пользуясь этими правилами, следует мысленно представлять себе сечение балки жестко защемленным, а связи отброшенными и замененными реакциями.
Подчеркнем, что для определения опорных реакций пользуются правилами знаков статики; для определения знаков изгибающего момента и поперечной силы — правилами знаков сопротивления материалов.
Правило знаков для изгибающих моментов иногда называют «правилом дождя» (имея в виду, что в случае выпуклости вниз образуется воронка, в которой задержится дождевая вода, и наоборот).
23.3. Дифференциальные зависимости при изгибе
Между изгибающим моментом, поперечной силой и интенсивностью распределенной нагрузки существуют дифференциальные зависимости, основанные на теореме Журавского, названной по имени замечательного русского инженера-мостостроителя Д.И.Журавского (1821 — 1891). Эта теорема формулируется так; поперечная сила равна первой производной от изгибающего момента по абсциссе сечения балки.
Рассмотрим балку (рис. 23.7). Начало координат возьмем на левом конце балки, а ось z направим вправо (в дальнейшем это будет иметь существенное значение).
На одном из участков балки возьмем сечение с текущей координатой z и запишем уравнение изгибающего момента:
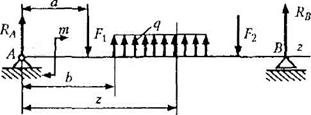
Рис. 23.7
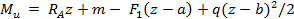
Продифференцировав это выражение по координате z получим
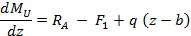
Выражение, стоящее в правой части этого равенства, есть поперечная сила Q в сечении z . Таким образом, теорема доказана.

Если уравнение изгибающих моментов (для участков с равномерно распределенной нагрузкой) продифференцировать вторично, то получим
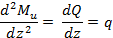
т.е. вторая производная от изгибающего момента или первая производная от поперечной силы по абсциссе сечения балки равна интенсивности распределенной нагрузки.
Как известно из высшей математики, по знаку второй производной функции можно судить о выпуклости или вогнутости кривой; соответствующее правило следует использовать при построении эпюр.
Эпюры поперечных сил и изгибающих моментов
Для наглядного изображения распределения вдоль оси балки поперечных сил и изгибающих моментов строят эпюры, которые дают возможность определить предположительно опасное сечение балки и установить значения поперечной силы и изгибающего момента в этом сечении.
Эпюры поперечных сил и изгибающих моментов можно строить двумя способами.
Первый способ заключается в том, что сначала составляют аналитические выражения поперечных сил и изгибающих моментов для каждого участка как функций текущей координаты z поперечного сечения:

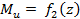
Затем по полученным уравнениям строят эпюры.
Второй способ заключается в построении эпюр по характерным точкам и значениям поперечных сил и изгибающих моментов на границах участков. Применяя этот способ, в большинстве случаев можно обойтись без составления уравнений поперечных сил и изгибающих моментов. При наличии некоторого опыта второй способ предпочтительнее.
При построении эпюр следует руководствоваться приведенными ниже правилами:
Эпюру моментов строят на сжатом волокне, т.е. положительные моменты (и положительные поперечные силы) откладывают
вверх от оси, а отрицательные — вниз.
Пользуясь принципом смягченных граничных условий, будем
полагать, что в сечении, где приложена сосредоточенная сила, значение поперечной силы меняется скачкообразно, причем скачок равен модулю этой силы.
На том же основании будем полагать, что в сечении, где приложена пара сил (момент), значение изгибающего момента меняется скачкообразно, причем скачок равен моменту нары.
Правильность построения эпюр следует проверять с помощью теоремы Журавского.
Как известно из математики, если  то
то
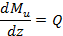
где а — угол, который составляет касательная к эпюре моментов с положительным направлением оси г. Согласно теореме Журавского,
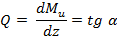
(масштабы Ми и z полагаем численно равными единице), следовательно, если угол а острый, то Q > 0 и изгибающий момент на участке возрастает; если угол а тупой, то Q < О и изгибающий момент на участке убывает; если a = 0 на всем участке, то Ми = const, Q = 0 и на этом участке возникает чистый изгиб; если a = 0 в одной точке эпюры моментов, то в этом сечении Q - 0, а изгибающий момент имеет экстремальное (максимальное или минимальное) значение. В сечении, где на эпюре поперечных сил имеется скачок, на эпюре изгибающих моментов будет резкое изменение направления касательной.
 Чтобы правила знаков для изгибающих моментов и поперечных сил. не противоречили знакам, полученным на основании теоремы Журавского, при проверке эпюр следует ось z мысленно всегда направлять слева направо.
Чтобы правила знаков для изгибающих моментов и поперечных сил. не противоречили знакам, полученным на основании теоремы Журавского, при проверке эпюр следует ось z мысленно всегда направлять слева направо.
На участке, где нет распре
деленной нагрузки, эпюра мо ментов представляет собой наклонную прямую, а эпюра поперечных
сил — прямую, параллельную оси.
На участке, где приложена равномерно распределенная нагрузка, эпюра моментов представляет собой параболу, а эпюра по перечных сил — наклонную прямую.
На конце балки изгибающий момент равен нулю, если там не приложена пара сил.
При построении эпюры для консольных балок начало координат удобно брать на конце консоли, что нередко дает возможность
обойтись без определения опорных реакций. В сечении, соответствующем заделке, поперечная сила равна реактивной силе, а изги бающий момент — реактивному моменту.
Пример 23.1. Построить эпюры поперечных сил и изгибающих моментов для балки, шарнирно закрепленной двумя концами и нагруженной сосредоточенной силой (рис. 23.8).
Решение. Начало координат поместим на левом конце балки, а ось направим вправо. Данная балка состоит из двух участков.
Определим опорные реакции RA и RB , составив уравнения моментов относительно опор А и В:
 ;
; 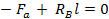 , откуда
, откуда 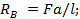
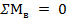 ;
; 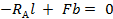 , следовательно,
, следовательно, 
Проверим правильность определения реакций, составив уравнение проекций на ось у:
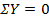 ;
; 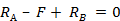

Полученное тождество 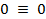 говорит о том, что реакции определены правильно
говорит о том, что реакции определены правильно
Приступаем к построению эпюр, применяя для этого метод сечений.
Построение эпюры поперечных сил. На первом участке поперечная сила Q 1 положительна, постоянна и равна RA , так как слева от сечения 1—1 других сил нет.
Откладываем вверх от оси эпюры в произвольном масштабе
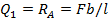 ; затем проводим прямую, параллельную оси эпюры.
; затем проводим прямую, параллельную оси эпюры.
Значение поперечной силы на втором участке будет равно Q 2 :
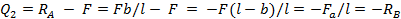
(то же получим, если рассмотрим часть балки, расположенную справа от сечения 2-2).
В точке приложения сосредоточенной силы F эпюра Q имеет скачок, численно равный F .
Вид эпюры Q показан на рис. 23.8.
Построение эпюры изгибающих моментов. В сечении 1-1 на первом участке изгибающий момент равен 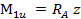 , причем z изменяется от 0 до а. Поскольку z входит в это уравнение в первой степени, эпюра моментов будет представлять собой прямую линию.
, причем z изменяется от 0 до а. Поскольку z входит в это уравнение в первой степени, эпюра моментов будет представлять собой прямую линию.
Для построения эпюры 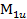 , достаточно найти значения моментов на границах участка, т.е. при z = 0 и z = а:
, достаточно найти значения моментов на границах участка, т.е. при z = 0 и z = а:
при z = 0 М1и = 0; при z = a 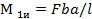
Для определения изгибающего момента в сечении 2—2 проще рассмотреть правую часть балки, на которую действует одна сила:

причем z меняется от а до l.
Эпюра моментов на втором участке также будет изображаться прямой линией. Найдем значения изгибающего момента на границах участка:
при 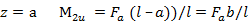 ;
;
при 
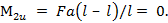
По полученным значениям строим эпюру  . Наибольшее значение
. Наибольшее значение  будет иметь в сечении, где приложена сила F :
будет иметь в сечении, где приложена сила F :
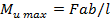
Это сечение будет предположительно опасным.
В частном случае, когда сила F приложена в середине балки.
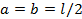 u
u 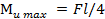
Пример 23.2. Построить эпюры поперечных сил и изгибающих моментов для балки, шарнирно закрепленной двумя концами и нагруженной парой сил с моментом m (рис. 239).
Р е ш е н и е. Выберем начало координат на левой опоре, а ось z направим вправо. Балка имеет два участка. Так как пару сил можно уравновесить только парой, то 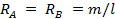 .
.
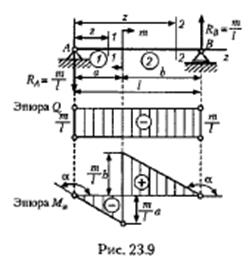 Построение эпюры поперечных сил. Для всех сечений первого и второго участков поперечная сила Q будет постоянна, отрицательна и равна
Построение эпюры поперечных сил. Для всех сечений первого и второго участков поперечная сила Q будет постоянна, отрицательна и равна 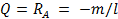 . Следовательно, эпюра будет прямой линией, параллельной оси.
. Следовательно, эпюра будет прямой линией, параллельной оси.
Построение эпюры изгибающих моментов. На первом участке 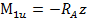 , причем z меняется от 0 до а:
, причем z меняется от 0 до а:
при z = 0 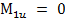 ;
;
при z = а 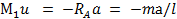 .
.
На втором участке 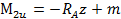 причем z меняется от а до
причем z меняется от а до  :
:
при z =а 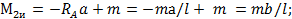
при z = 
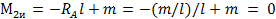
Эпюру Ми часто можно построить, не составляя уравнений, по значениям Ми на границах участков.
Пользуясь ранее приведенными правилами, устанавливаем, что на концах балки Ми = 0; в сечениях, бесконечно близких к паре сил слева и справа от нее, изгибающий момент
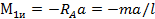 ;
; 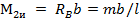 .
.
В точке приложения пары сил эпюра Ми имеет «скачок», величина которого равна моменту пары.
Построенная по найденным значениям эпюра Ми показана на рис. 23.9. Заметим, что на основании теоремы Журавского

следовательно, наклонные линии эпюры Ми на обоих участках должны быть параллельны между собой.
Полагая b > а, находим наибольшее значение изгибающего момента:
Ми max = mb/ 
В частном случае, когда внешний момент m приложен в середине пролета балки,
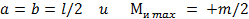
Пример 23.3. Построить эпюры поперечных сил и изгибающих моментов для балки, свободно лежащей на двух опорах и нагруженной равномерно распределенной нагрузкой интенсивности q (рис. 23.10).
Решение. В силу симметричности распределения нагрузки по всей длине балки опорные реакции равны между собой:
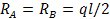
 Построение эпюры поперечных сил. Данная балка имеет один участок. В любом сечении поперечная сила
Построение эпюры поперечных сил. Данная балка имеет один участок. В любом сечении поперечная сила

Поскольку z входит в это уравнение в первой степени (линейная зависимость), то эпюра Q будет прямолинейной. Для построения эпюры достаточно значений поперечной силы в двух точках:
при z=0 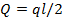
при z = 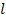
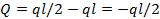
Эпюра Q показана на рис. 23.10.
Построение эпюры изгибающих моментов. Выражение для изгибающего момента в любом сечении балки имеет вид

Это уравнение параболы. Определим значения 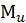 :
:
при  ;
;

при 

Очевидно, что при z = l Мu = 0.
По найденным значениям строим эпюру Ми, как показано на рис. 23.10.
Поскольку вторая производная
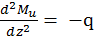
т. меньше нуля, то эпюра Ми будет расположена выпуклостью вверх.
Согласно теореме Журавского максимальное значение изгибающего момента будет в середине пролета балки, где
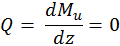
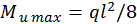
Пример 23.4. Построить эпюры поперечных сил и изгибающих моментов для консольной балки АС, свободно лежащей на двух опорах и нагруженной равномерно распределенной нагрузкой интенсивности q = 200 Н/м, как показано на рис. 23.11.
Решение. Определим реакцииRA и RB :
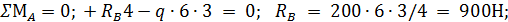
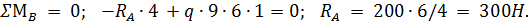
Переходим к построению эпюры Q . Балка имеет два участка.
На первом участке поперечная сила 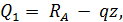 причем z меняется от 0 до 4 м:
причем z меняется от 0 до 4 м:
при z = 0 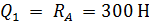 ;
;
при z = 4 м 
Для упрощения построения эпюры Q на втором участке возьмем начало координат в точке С и направим ось z влево, тогда Q 2 = qz , причем z меняется от 0 до 2 м:
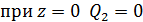
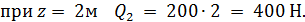
На границе участков в точке В эпюра Q имеет «скачок», равный по величине опорной реакции RB = 900 Н.
Найдем точку оси, в которой Q = 0. Для этого запишем
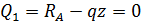
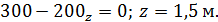
На основании теоремы Журавского можно ожидать в этой точке экстремальное значение изгибающего момента. Переходим к построению эпюры Мм. На первом участке выражение для изгибающего момента имеет вид
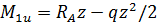
Эпюра Ми будет представлять собой параболу. Вычислим значения М!и в трех точках:

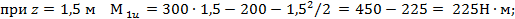

Для второго участка, взяв за начало координат точку С, получим

Вычислим значение М2и на границах участка:

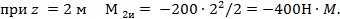
По найденным значениям строим эпюру Ми.
Поскольку в данном примере 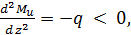 эпюра Mu, на обоих участках будет направлена выпуклостью вверх.
эпюра Mu, на обоих участках будет направлена выпуклостью вверх.
Из построенных эпюр видно, что опасным будет сечение балки на опоре В.
Дата добавления: 2021-05-18; просмотров: 77; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
