Перечень основной и дополнительной учебной литературы,
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ГРАЖДАНСКОЙ АВИАЦИИ
_________________________________________________________________
В.В. Пермякова
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
УСТАНОВОЧНАЯ ЛЕКЦИЯ
УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ
для студентов 1 курса
по направлению подготовки 25.03.01
заочной формы обучения
Москва – 2017
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ВОЗДУШНОГО ТРАНСПОРТА
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ
БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ОБРАЗОВАНИЯ
«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ ГРАЖДАНСКОЙ АВИАЦИИ» (МГТУ ГА)
_____________________________________________________________________________
Кафедра технической механики и инженерной графики
В.В. Пермякова
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
УСТАНОВОЧНАЯ ЛЕКЦИЯ
УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ
для студентов 1 курса
по направлению подготовки 25.03.01
заочной формы обучения
Москва – 2017
ББК 531
П
Рецензент: к.т.н., доц. В. К. Харина
Пермякова В.В.
Теоретическая механика. Установочная лекция: Учебно-методическое пособие. - М.: МГТУ ГА, 2017.
Данное пособие издается в соответствии с учебным планом для студентов 1 курса по направлению подготовки 25.03.01 заочной формы обучения.
Рассмотрено и одобрено на заседаниях кафедры «Техническая механика и инженерная графика» …. ……….. 2017 г. и методического совета механического факультета …………… 2017 г.
|
|
|
Стремительное развитие Российской авиационной техники сопровождается коренными изменениями и значительными усовершенствованиями всей многообразной материальной части летательного аппарата. Чтобы освоить современную авиационную технику, чтобы умело ее обслуживать и рационально эксплуатировать, надо сочетать практический опыт с теоретической подготовкой. При этом следует помнить, что успешное и сознательное овладение теоретическими основами авиационной техники невозможно без знания общих законов теоретической механики.
При изложении материала принято обычное деление науки теоретической механики на разделы: статика, кинематика и динамика.
В статике рассматриваются условия равновесия твердых тел, в кинематике изучаются геометрические характеристики механического движения тел независимо от взаимодействия между ними и в динамике устанавливаются общие законы механических движений, взаимодействующих тел.
Статика
Понятие силы является одним из основных понятий в механике. Это понятие неразрывно связано с представлением о переносе или передаче движения с одного тела на другое. Всякая сила имеет точку приложения, определенную величину и определенное направление. Значит, сила - вектор. Графически вектор силы изображают в виде отрезка прямой, длина которого в масштабе выражает численное значение силы, а направление, отмеченное стрелкой, указывает направление силы.
|
|
|
Векторы сил будем обозначать буквами, напечатанными обыкновенным шрифтом с чертами над ними, например 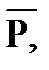
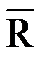 ,
,  и т.п.
и т.п.
Численные величины сил будем обозначать теми же буквами, что и векторы, но без черты над ними.
Например,
P – численная величина силы  ;
;
R – численная величина силы  .
.
В технике за единицу измерения силы принимают ньютон, используя систему “СИ”.
Если заданы две силы, приложенные к общей точке, то можно найти их сумму (равнодействующую силу), применяя правило векторного сложения, на основании которого сумма этих сил равна диагонали параллелограмма, построенного на этих силах, как на сторонах.
Сила – мера механического взаимодействия материальных тел, в результате которого взаимодействующие тела могут сообщать друг другу ускорения или деформироваться (изменять свою форму).
|
|
|
Однако, рассматривая действие сил на материальные тела, мы будем пренебрегать деформацией этих тел, пользуясь моделью абсолютно твердого тела. Тело называют абсолютно твердым, если расстояние между двумя любыми точками тела остается постоянным, независимо от действующих на тело сил.
В материальном мире не существует ни одного тела, которое не подвергалось бы воздействию со стороны других тел. Если в результате действия нескольких сил характер движения твердого тела не изменяется, то говорят, что силы, приложенные к данному твердому телу, взаимно-уравновешены или находятся в равновесии.
В практике инженерного дела большое значение имеет задача об отыскании условий равновесия сил, приложенных к какой-нибудь реальной конструкции или части ее. Однако, следует заметить, что было бы в корне неверно связывать равновесие сил, приложенных к твердому телу, исключительно с покоем тела. Под действием таких сил тело может находиться и в состоянии равномерного и прямолинейного движения. Примером такого движения может служить горизонтальный установившийся полет самолета.
Решение задач статики основано на применении метода проекций. Рассматриваемую систему сил помещают в прямоугольную (декартову) систему неподвижных осей (XOY). Проекцией сил на ось называется алгебраическая (скалярная) величина направленного отрезка оси, заключенного между проекциями начала и конца силы. Проекция силы 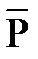 характеризуется не только абсолютной величиной (модулем), но и знаком.
характеризуется не только абсолютной величиной (модулем), но и знаком.
|
|
|
Проекция силы на каждую координатную ось определяется произведением модуля силы на косинус острого угла между направлениями оси и силы. Если известны проекции силы, лежащие в одной плоскости, на взаимно-перпендикулярные оси ОХ, ОУ, то модуль силы определяется по формуле: Р = 
Отметим частные случаи:
1. Сила перпендикулярна к оси проекций. В этом случае сила проектируется в точку.
Проекция силы на ось ОХ равна нулю.
2. Сила параллельна оси проекций. В этом случае сила проектируется в натуральную величину.
Проекция силы на ось ОХ равна величине силы, взятой со знаком «+» или «-» в зависимости от положения силы относительно оси проекций.
Момент силы относительно точки
Момент силы 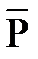 относительно какой-либо точки (центра) “O” называется вектор, численно равный произведению модуля силы Р на плечо h, т.е. на кратчайшее расстояние от указанной точки до линии действия силы.
относительно какой-либо точки (центра) “O” называется вектор, численно равный произведению модуля силы Р на плечо h, т.е. на кратчайшее расстояние от указанной точки до линии действия силы.
Если линия действия силы проходит через неподвижную точку (центр) “O”, в этом случае плечо силы и момент силы относительно неподвижной точки “O” равны нулю.
Условимся считать момент силы относительно данной точки положительным, если сила стремится повернуть тело вокруг данной точки против движения часовой стрелки, и отрицательным, если сила стремится повернуть тело по ходу часовой стрелки.
Из определения момента силы относительно точки, как произведения силы на плечо, вытекают единицы измерения момента, например, в системе “СИ” – Нм.
При определении плеча следует иметь в виду, что это перпендикуляр, опущенный из центра момента на линию действия силы.
Вектор момента силы 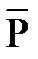 относительно центра “O” изображается вектором
относительно центра “O” изображается вектором  о, приложенным в центре “O”, перпендикулярным плоскости “П”, проходящей через выбранную точку и линию действия силы в ту сторону, откуда ”вращение”, совершаемое силой вокруг точки, представляется происходящим против хода часовой стрелки.
о, приложенным в центре “O”, перпендикулярным плоскости “П”, проходящей через выбранную точку и линию действия силы в ту сторону, откуда ”вращение”, совершаемое силой вокруг точки, представляется происходящим против хода часовой стрелки.
Для определения момента силы для плоской системы сил можно использовать теорему о моменте равнодействующей силы – теорему Вариньона: момент  о(
о( 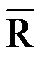 ) равнодействующей
) равнодействующей  плоской системы сил
плоской системы сил  1 и
1 и  2, приложенных в точке А относительно произвольной точки О на плоскости, равен алгебраической сумме моментов
2, приложенных в точке А относительно произвольной точки О на плоскости, равен алгебраической сумме моментов  о(
о( 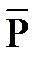 1) и
1) и  о(
о( 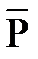 2) составляющих сил относительно той же точки. Применение этой теоремы упрощает решение задачи.
2) составляющих сил относительно той же точки. Применение этой теоремы упрощает решение задачи.
Следовательно,  о(
о( 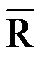 ) =
) =  о(
о( 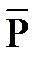 1) +
1) +  о(
о( 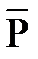 2)
2)
Аксиомы статики
В аксиомах статики формулируются простейшие и общие законы, которым подчиняются силы, действующие на тела. Эти законы установлены многочисленными непосредственными наблюдениями.
Аксиома I . Две силы, приложенные к абсолютно твердому телу, будут уравновешены (эквивалентны нулю), тогда и только тогда, когда они равны по модулю, действуют по одной прямой и направлены в противоположные стороны.
Аксиома 2. Не нарушая состояния абсолютно твердого тела, к нему можно прикладывать или отбрасывать силы тогда и только тогда, когда они составляют уравновешенную систему.
Следствие. Не нарушая кинематического состояния тела, точку приложения сил можно переносить вдоль линии ее действия.
Аксиома 3. (Аксиома параллелограмма сил). Не меняя кинематического состояния тела, две силы, приложенные к одной его точке, можно заменить одной равнодействующей силой, приложенной в той же точке и равной их геометрической сумме.
Пусть имеем подъемную силу крыла  и силу лобового сопротивления крыла
и силу лобового сопротивления крыла  . Полная аэродинамическая сила будет равна равнодействующей
. Полная аэродинамическая сила будет равна равнодействующей  этих сил.
этих сил.
Аксиома 4 (3-й закон Ньютона). Силы взаимодействия двух тел равны по модулю и направлены по одной прямой в противоположные стороны.
Аксиома 5. Равновесие деформируемого тела не нарушается, если жестко связать его точки и считать тело абсолютно твердым.
Связи и реакции связей
Тело называется свободным, если оно может получить любое перемещение в пространстве, например, самолет и воздушный шар в полете. Если же возможность перемещения тела в пространстве ограничена, то такое тело называют несвободным.
Тела, стесняющие движение данного тела, называются связями. Например, самолет на посадочной площадке, привязной аэростат, поршень в цилиндре – тела несвободные. В первом случае связью является поверхность площадки, во втором – торс, в третьем – стенки цилиндра.
Сила, с которой связь действует на данное тело, называется реакцией связи или реакцией.
Одним из основных положений механики является принцип освобождения твердых тел от связей, согласно которому несвободное тело можно рассматривать как свободное, на которое, кроме задаваемых сил, действуют реакции связей.
Нахождение реакций связи представляет одну из весьма важных технических задач. Рассмотрим примеры связей и их реакций.
Гладкая опорная плоскость
Самолет опирается колесами шасси на гладкую горизонтальную площадку.
Через колеса шасси на площадку передаются силы  А и
А и  В.
В.
Эти силы направлены по вертикали вниз и приложены к площадке в точках А и В касания колес шасси и площадки. Реакции  А и
А и 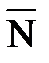 В гладкой площадки направлены вертикально вверх, т.е. перпендикулярно к опорной плоскости, и приложены к колесам в точках А и В касания колес шасси и опорной плоскости.
В гладкой площадки направлены вертикально вверх, т.е. перпендикулярно к опорной плоскости, и приложены к колесам в точках А и В касания колес шасси и опорной плоскости.
Реакция гладкой опорной плоскости всегда направлена перпендикулярно к этой плоскости или, как говорят, нормально к плоскости. При опробовании мотора главные колеса уперты в площадки. В этом случае покрышка пневматика опирается на точку Д колодки. Реакция опорной точки приложена к колесу и проходит через центр его, т.е. направлена по нормали колеса. Реакция направлена по нормали к опирающемуся колесу.
Гибкая связь
При транспортировке вертолетами грузов на внешней торсовой подвеске реакции троса направлены вдоль торса.
Шарнир
Шарнир является связью, которая обеспечивает вращение одного тела относительно другого вокруг центра, или, точнее вокруг оси шарнира. Лопасти вертолета крепятся к ротору при помощи горизонтального и вертикального шарниров.
Подшипник, подпятник
Подшипники являются основной частью опоры вала. Различают радиальные подшипники и упорные.
Радиальные подшипники или подшипники обеспечивают вращение вала вокруг продольной оси и допускают смещение вала вдоль этой оси. Реакции подшипника всегда нормальна к оси вала.
Упорные подшипники или подпятники обеспечивают вращение вала вокруг продольной оси, но препятствуют смещению вала вдоль этой оси.
Плоская система сил
Система сил, линии действия которых не пересекаются в одной точке и не параллельны, называется плоской системой сил.
Примером плоской системы сил могут служить силы, действующие на самолет в полете. Вследствие геометрической и весовой симметрии самолета можно считать, что силы лежат в вертикальной плоскости симметрии, проходящей через продольную ось самолета.
Условия равновесия плоской системы сил
Рассмотрим случай, когда плоская система сил находится в равновесии.
Для равновесия плоской системы сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил этой системы на каждую их двух координатных осей равнялась нулю, и алгебраическая сумма моментов этих сил относительно любой точки в плоскости также равнялась нулю.
ΣFкх = 0 ΣFку = 0 ΣМо =0 (1)
Уравнения (1) называются уравнениями равновесия плоской системы сил.
В некоторых случаях уравнения равновесия целесообразнее составлять в другой форме.
Если в плоскости действия сил взять три точки О1, О2, О3, не лежащих на одной прямой, то уравнения равновесия плоской системы сил можно записать в виде:
ΣМо1( 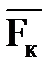 ) = 0 ΣМо2(
) = 0 ΣМо2(  ) = 0 ΣМо3(
) = 0 ΣМо3(  ) = 0,
) = 0,
т.е. для равновесия плоской системы сил необходимо и достаточно, чтобы алгебраическая сумма моментов всех сил относительно каждой из трех точек, произвольно взятых в плоскости действия сил и не лежащих на одной прямой, равнялась нулю.
Если вместо одного из уравнений моментов, например, третьего, составить уравнение проекций сил на произвольную
ось У, не перпендикулярную к прямой О1, О2, то получим еще один вариант уравнений равновесия произвольной плоской системы сил
ΣМо1( 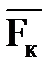 ) = 0 ΣМо2(
) = 0 ΣМо2(  ) = 0 ΣFку = 0 , который сводится к тому, что для равновесия плоской системы сил необходимо и достаточно, чтобы алгебраическая сумма моментов всех сил относительно каждой из двух точек, произвольно взятых в плоскости действия сил, равнялась нулю и алгебраическая сумма проекций этих сил на любую ось, не перпендикулярную к прямой, проходящей через центры моментов, также равнялась нулю.
) = 0 ΣFку = 0 , который сводится к тому, что для равновесия плоской системы сил необходимо и достаточно, чтобы алгебраическая сумма моментов всех сил относительно каждой из двух точек, произвольно взятых в плоскости действия сил, равнялась нулю и алгебраическая сумма проекций этих сил на любую ось, не перпендикулярную к прямой, проходящей через центры моментов, также равнялась нулю.
На применении этих и ряда других уравнений основан аналитический метод решения задач плоской статики.
Задачи статики, которые могут быть решены при помощи уравнений статики твердого тела, называются статически определенными. Так как число уравнений равновесия плоской системы сил равно трем, то задача о равновесии твердого тела, находящегося под действием плоской системы сил, - статически определенная, если число неизвестных в ней равно трем.
Общий план решения задачи статикианалитическим способом
1. Выявить тело, равновесие которого надо рассмотреть.
2. Выяснить заданные силы, приложенные к этому телу.
3. Выбрать оси координат.
4. Отбросить связи, наложенные на тело и заменить их соответствующими силами реакций.
5. Выбрать центр моментов.
6. Составить уравнения равновесия и решить их.
Кинематика
В основе всех явлений, происходящих в природе и во внешнем мире, лежит движение материи. Наблюдая движение окружающих тел, можно заметить, что в одних случаях все точки твердого тела движутся совершенно одинаково, в других же случаях разные точки твердого тела движутся различно. Так, например, в работающем авиационном двигателе все точки поршня движутся совершенно одинаково, проходя по параллельным прямым за один и тот же промежуток времени равные пути.
Точки кривошипа движутся различно, проходя по окружностям разных радиусов за один и тот же промежуток времени разные пути.
Движение поршня относительно цилиндра называют поступательным. Движения кривошипа называют вращательным вокруг неподвижной оси.
Движение твердого тела называется поступательным, если любая прямая, проведенная в этом теле, во все время движения остается параллельной своему первоначальному положению.
Положение движущейся точки будем определять по отношению к неподвижной системе отсчета. Последовательные положения точки, движущейся в пространстве относительно выбранной системы отсчета, образуют линию, которая называется траекторией точки. По форме траектория может быть прямой или кривой линией. В связи с этим различают прямолинейное и криволинейное движения точки.
Способы задания движения точки
1. Векторный способ задания движения точки
Положение точки определяется с помощью радиуса – вектора  , проведенного из неподвижного центра “O” в точку М.
, проведенного из неподвижного центра “O” в точку М.
Уравнение движения точки 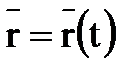 .
.
Скорость точки – векторная величина, характеризующая быстроту и направление движения точки 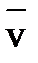 =
=  . Вектор скорости направлен всегда по касательной к траектории движения.
. Вектор скорости направлен всегда по касательной к траектории движения.
Ускорение точки – векторная величина, характеризующая быстроту изменения модуля и направления скорости точки  =
= 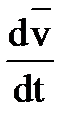 .
.
2. Координатный способ задания движения точки
Положение точки М в декартовой системе координат определяется координатами X, Y, Z.
а) уравнения движения точки в пространстве x=x(t), y=y(t), z=z(t)
б) уравнения движения точки на плоскости x=x(t), y=y(t)
в) уравнение прямолинейного движения точки x=x(t)
Скорость точки  ,
,
где vx = 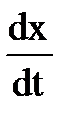 , vy =
, vy =  , vz=
, vz= 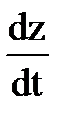 .
.
Ускорение точки a =  ,
,
где ax = 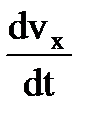 , ay =
, ay = 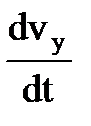 , az =
, az = 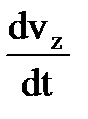 .
.
3. Естественный способ задания движения точки
Траектория точки М заранее известна.
Точка О – начало отсчета. Положение точки М определяется дуговой координатой S, т.е. расстоянием ОМ = s от начала отсчета.
Уравнение движения точки s=s(t).
При естественном задании движения точки на плоскости применяют естественные оси: n – нормальная ось; τ – касательная ось.
Скорость точки v = 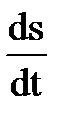 .
.
Ускорение точки a = 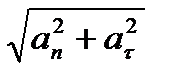 ,
,
где an, aτ - проекции на естественные оси (нормальное и касательное ускорение): an =  ; aτ =
; aτ = 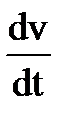 , где
, где
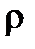 - радиус кривизны траектории в данной точке.
- радиус кривизны траектории в данной точке.
Если пройденный путь измеряется в метрах, а время измерено в секундах, то скорость будет выражена в м·с-1, а ускорение в м·с-2
Полезно запомнить, что 1 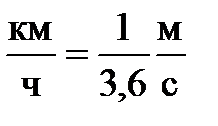 ; 1
; 1 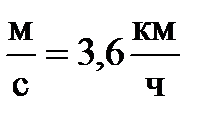 .
.
Поступательное движение твердого тела
Поступательным движением твердого тела называется такое движение, при котором любая прямая, проведенная в теле, остается во все время движения параллельной своему первоначальному положению. Примером прямолинейного поступательного движения может служить горизонтальный установившийся полет самолета. При поступательном движении твердого тела траектории точек одинаковы, скорости и ускорения всех точек в каждый момент времени равны между собой.
Для определения поступательного движения твердого тела достаточно рассмотреть движение одной точки тела.
Вращение твердого тела вокруг неподвижной оси
Движение твердого тела называется вращением вокруг неподвижной оси, если одна прямая, неизменно связанная с твердым телом, во время движения остается неподвижной. Эта неподвижная прямая называется осью вращения. Центробежный компрессор и газовая турбина реактивного двигателя, винт самолета вращаются вокруг неподвижных осей.
Уравнение вращательного движения твердого тела - φ = φ(t), где
φ - угол поворота твердого тела вокруг неподвижной оси. Существует два способа измерения углов: в градусах и в радианах. Переход от радианной меры к градусной производится на основании следующих формул:
1 рад = 57,3о; 1 град = 0,017 рад
Вращение твердого тела вокруг неподвижной оси называется равномерным, если в любые равные промежутки времени тело поворачивается на одинаковые углы. В равномерном вращении твердого тела вокруг неподвижной оси отношение угла поворота к промежутку времени, в течение которого тело повернулось на этот угол, сохраняет постоянное значение. Это постоянное отношение называют угловой скоростью тела в равномерном вращении вокруг неподвижной оси. Обозначим угловую скорость буквой ω.
Положим, что тело, равномерно вращаясь, за промежуток времени t поворачивается на угол φ, тогда по определению угловой скорости будем иметь ω = 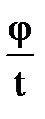 .
.
Вращение твердого тела вокруг неподвижной оси называют неравномерным, если ω =  имеет переменное значение.
имеет переменное значение.
На практике угловую скорость вращающихся тел, в частности, валов реактивных двигателей самолетов, задаются числом n оборотов в минуту.
Установим связь между угловой скоростью ω, выраженной в 1/с и числом n, выраженной в об/мин:  .
.
Все точки тела, вращающегося вокруг неподвижной оси, описывают окружности разных радиусов. Эти окружности расположены в плоскостях, перпендикулярных оси вращения, а их центры лежат на этой оси.
Рассмотрим движение одной точки тела, вращающегося вокруг неподвижной оси. Эта точка описывает окружность, радиус которой равен расстоянию R = OA от оси вращения до точки А. Величина линейной скорости v точки А тела, вращающегося равномерно вокруг неподвижной оси O, пропорционально расстоянию R этой точки до оси, при этом коэффициентом пропорциональности является угловая скорость: v = ωR.
Вектор линейной скорости 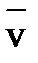 откладывается по касательной к окружности в данной точке и всегда направлен в сторону вращения.
откладывается по касательной к окружности в данной точке и всегда направлен в сторону вращения.
Плоское движение твердого тела
Плоским движением твердого тела называется такое движение, при котором каждая точка тела движется в плоскости, параллельной некоторой неподвижной плоскости.
Движение шатуна АВ в шатунно-кривошипном механизме авиационного двигателя, качение колеса самолета по прямолинейной взлетно-посадочной полосе является плоским или плоско-параллельным движением.
Всякое непоступательное перемещение плоской фигуры в ее плоскости можно рассматривать как совокупность двух перемещений: поступательного перемещения плоской фигуры вместе с произвольной точкой, называемой полюсом, и поворота вокруг этого полюса. Следовательно, действительное движение плоской фигуры в ее плоскости в каждый момент времени можно рассматривать как совокупность поступательного движения и вращения.
Пусть точка О – полюс; хо, уо - координаты полюса.
Тогда уравнения плоского движения твердого тела имеют вид:
хо = f1(t) уо = f2(t) φ = f3(t).
Скорость любой точки тела складывается геометрически из скорости полюса vо и вращательной скорости vмо этой точки во вращательном движении фигуры вокруг полюса.
Вращательная скорость 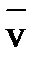 мо точки М во вращательном движении вокруг полюса О: vмо = ω·МО
мо точки М во вращательном движении вокруг полюса О: vмо = ω·МО
Мгновенный центр скоростей
В каждый момент времени существует точка, неизменно связанная с плоской фигурой, скорость которой в этот момент времени равна нулю. Эту точку называют мгновенным центром скоростей (м.ц.с.). Обычно эту точку обозначают буквой Р.
Зная положение мгновенного центра скоростей, можно найти скорости всех точек плоской фигуры, т.к. скорость любой точки тела, совершающего плоское движение, равна вращательной скорости этой точки вокруг мгновенного центра скоростей.
Если тело движется не поступательно, то мгновенный центр скоростей Р лежит на пересечении перпендикуляров Аа и Вв к векторам 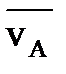 и
и  .
.
Угловая скорость тела ω. Тогда vA = ω·PА; vВ = ω·PВ
Следовательно: 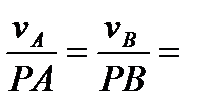 ω.
ω.
Скорости точек тела пропорциональны их расстояниям до мгновенного центра скоростей.
Отношение скорости какой-либо точки тела к ее расстоянию до мгновенного центра скоростей определяет угловую скорость тела.
Если скорости точек А и В параллельны и  ┴ АВ, то надо соединить концы векторов
┴ АВ, то надо соединить концы векторов 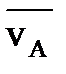 и
и  линией до пересечения с продолжением АВ. Точка Р – мгновенный центр скоростей тела.
линией до пересечения с продолжением АВ. Точка Р – мгновенный центр скоростей тела.
Если 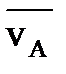 и
и  параллельны, но
параллельны, но 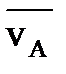 не перпендикулярна отрезку АВ, то в этом случае мгновенный центр скоростей находится в бесконечности. Угловая скорость ω=0. Тело совершает мгновенно поступательное движение. В задаче К2 плоское движение совершают стержни 2 и 3.
не перпендикулярна отрезку АВ, то в этом случае мгновенный центр скоростей находится в бесконечности. Угловая скорость ω=0. Тело совершает мгновенно поступательное движение. В задаче К2 плоское движение совершают стержни 2 и 3.
Динамика
Теоретическая механика изучает простейшую форму движения материи – механическое движение, т.е. простую перемену места в пространстве с течением времени. Движение самолета, отдельных частей двигателя – все это примеры механического движения. Раздел теоретической механики – динамика устанавливает общие законы механического движения.
Динамика изучает движение материальных тел, обусловленное их взаимодействием.
В основе динамики лежат три закона Ньютона. Эти законы обоснованы тысячелетним опытом и многовековой практической деятельностью человека. Чтобы установить общие свойства, присущие всем видам движения, будем принимать за систему отсчета оси координат, связанные с поверхностью земли. Эту систему отсчета будем считать условно “неподвижной” и будем пользоваться ею при изучении движений, происходящих на Земле. Следует отметить, что законы Ньютона вовсе не являются последними границами знания о движении, но они достаточно верно отображают свойства механического движения.
Законы динамики материальной точки
1. Первый закон Ньютона (закон инерции)
Изолированная материальная точка сохраняет состояние покоя или
равномерного и прямолинейного движения до тех пор, пока действие других тел не изменит этого состояния.
Если материальная точка движется с переменной по величине или направлению скоростью, то на нее обязательно действует некоторая сила. Действие этой силы обнаруживается в появлении ускорения. Первый закон Ньютона позволяет установить, приложена к данному телу сила или нет.
2. Второй закон Ньютона (закон пропорциональности)
Ускорение материальной точки пропорционально приложенной силе и
имеет одинаковое с ней направление.
Обозначим:
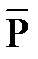 - действующая сила;
- действующая сила;
 - ускорение материальной точки;
- ускорение материальной точки;
m – масса материальной точки.
Получим следующее векторное уравнение m  =
=  .
.
Это уравнение носит название основного уравнения динамики. Чем больше масса материальной точки, тем большую силу надо приложить, чтобы получить данное ускорение. Это свойство называют инертностью материального объекта в механическом движении. За меру инертности принимают массу тела. Второй закон Ньютона позволяет определить величину и направление силы.
3. Третий закон Ньютона (о равенстве действия и противодействия0
Всякому действию соответствует равное и противоположно
направленное противодействие.
Например, движение вращающегося винта самолета передается окружающему воздуху: винт отбрасывает поток воздуха назад и одновременно сообщает воздуху вращательное движение. При этом возникает сила тяги, действующая на винт со стороны отброшенного назад воздуха и направленная вдоль оси винта вперед. Действие на винт со стороны закрученного воздуха создает так называемый реактивный момент, стремящийся повернуть самолет вокруг продольной оси в сторону, обратную вращению винта.
Третий закон Ньютона утверждает, что сила есть активное действие, переданное с одного тела на другое. При взаимодействии двух материальных точек ускорения, сообщаемые ими друг другу, всегда пропорциональны массам этих материальных точек.
4. Закон независимости действия сил
При действии на материальную точку нескольких сил ее ускорение
равно сумме ускорений, которые имела бы точка при действии каждой силы в отдельности.
Назовем 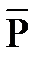 1 и
1 и  2 силы, действующие на материальную точку, тогда ускорение
2 силы, действующие на материальную точку, тогда ускорение  , которое эти силы сообщают материальной точке, найдем из уравнения m
, которое эти силы сообщают материальной точке, найдем из уравнения m  =
= 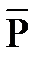 1 +
1 +  2 или
2 или  =
=  1 +
1 + 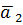 .
.
Обычно для решения практических задач основное уравнение динамики применяют не в векторной форме, а в форме проекций на прямоугольные оси координат. Эти уравнения будем называть уравнениями движения материальной точки в форме проекций на прямоугольные оси координат.
max = Px , may = Py , maz = Pz ,
где ax , ay , az - проекции ускорения материальной точки на оси Ox , Oy , Oz;
Px , Py , Pz - проекции силы 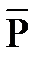 на те же оси.
на те же оси.
Если движение совершается на плоскости, то достаточно двух уравнений движения ax = Px , may = Py .
В случае прямолинейного движения точки достаточно оставить одно уравнение max = Px (1)
Две основные задачи динамики точки
Обозначим ax =  ay =
ay = 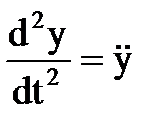 az =
az = 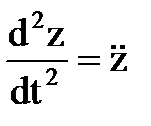
получим дифференциальные уравнения движения в прямоугольных координатах
m  = Px m
= Px m  = Py m
= Py m 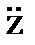 = Pz .
= Pz .
Дифференциальные уравнения движения позволяют решать две основные задачи динамики точки: прямую и обратную.
Первая задача динамики
В первой задаче динамики движение материальной точки является заданным и требуется найти силы, под действием которых это движение происходит, то есть, зная массу материальной точки “m” и уравнения ее движения в виде
x = x(t) y = y(t) z = z(t),
можно найти величину и направление равнодействующей сил, действующих на материальную точку. Продифференцировав уравнения движения два раза по времени и умножив на массу точки m, найдем проекции равнодействующей сил на координатные оси
Px = m  Py = m
Py = m  Pz = m
Pz = m 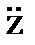 .
.
Модуль (величину) равнодействующей силы найдем по формуле
Р =  .
.
Наклон равнодействующей силы Р к осям Ох , Оу , Оz найдем через направляющие косинусы
cos  cos
cos 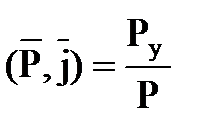 cos
cos 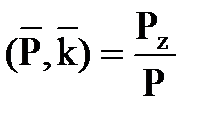 ,
,
где  - единичные орты (векторы единичной длины вдоль каждой оси координат).
- единичные орты (векторы единичной длины вдоль каждой оси координат).
Вторая задача динамики
Рассмотрим эту задачу более подробно, так как задача D1 контрольного задания предлагает вторую задачу динамики.
Во второй задаче динамики, зная массу материальной точки и силы
действующие на нее, найти уравнения движения точки, используя начальные условия в виде начальных координат и начальной скорости движения.
В декартовой системе координат нужно задать соответствующие проекции при t = 0
x = xo y = yo z = zo 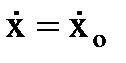

 (1)
(1)
Совокупность этих данных называется начальным условием движения.
Чаще всего на материальную точку одновременно действует несколько сил различных типов: силы могут зависеть от времени t , от положения точки х и от ее скорости vx = 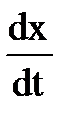 .
.
Покажем, как применять основное уравнение динамики к решению простейших динамических задач.
План решения второй задачи динамики
1. Отнести движение материальной точки к неподвижной системе прямоугольных координат, начало которой совместить с начальным положением материальной точки. В случае прямолинейного движения следует взять только одну ось и направить ее вдоль прямолинейной траектории.
2. Выяснить силы, приложенные к движущейся материальной точке, в произвольном положении точки.
3. Составить основное уравнение динамики в проекциях на выбранные оси координат.
4. На основании составленных уравнений установить характер движения.
5. В зависимости от характера движения написать соответствующие уравнения из кинематики и определить искомые величины.
В случае прямолинейного движения материальной точки уравнение
будет представлять собой дифференциальное уравнение 2-го порядка
m  , (2)
, (2)
где 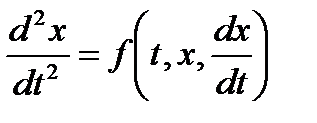 (3)
(3)
Для решения задачи следует проинтегрировать уравнение (2), в результате чего в решении будут иметь место две постоянные интегрирования, обозначаемые С1 и С2 . Значения постоянных интегрирования С1 и С2 можно найти, используя начальные условия (1).
Общие теоремы динамики системы
Главное значение общих теорем состоит в том, что они устанавливают зависимость между количеством движения, кинетической энергией и т.п. и силами, действующими на материальное тело (материальную точку).
Механическая система – совокупность материальных точек, в которой положение и движение каждой точки зависит от положения и движения всех остальных материальных точек.
Примером механической системы является самолет.
Рассмотрим силы, действующие на самолет. Как известно, самолет состоит из следующих основных частей: фюзеляжа, крыла, силовой установки, органов управления и устойчивости, шасси.
Силы, с которыми отдельные части самолета действуют друг на друга, будем называть внутренними силами. Силу тяжести, подъемную силу, лобовое сопротивление и др. будем называть внешними силами.
Внешние силы – силы, действующие на точки механической системы со стороны материальных точек, не входящих в состав данной механической системы.
Внутренние силы 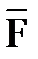 е - силы взаимодействия между материальными точками данной механической системы.
е - силы взаимодействия между материальными точками данной механической системы.
На основании третьего закона Ньютона о равенстве действия и противодействия геометрическая сумма всех внутренних сил механической системы равна нулю и сумма моментов всех внутренних сил системы относительно любого центра или оси равняется нулю.
Центр масс системы – точка, положение которой в каждый момент времени определено выражениями:
xc = 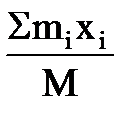 yc =
yc = 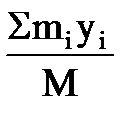 zc =
zc = 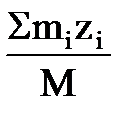 .
.
Теорема о движении центра масс
Центр масс механической системы движется как материальная точка массой, равной массе всей системы, к которой приложены все внешние силы, действующие на систему.
М  e ,
e ,
где М = 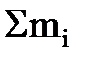 - масса механической системы;
- масса механической системы;
ac - ускорение центра масс системы;
N - количество материальных точек системы.
Если  = 0 , то
= 0 , то 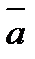 с = 0, и
с = 0, и 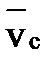 = соnst.
= соnst.
Теорема об изменении количества движения механической системы
Формулировка теоремы в дифференциальной форме
Производная по времени от количества движения механической системы геометрически равна главному вектору внешних сил, действующих на систему 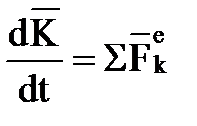 .
.
Количество движения системы ( 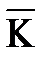 ) вектор, равный геометрической сумме количества движения
) вектор, равный геометрической сумме количества движения 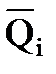 всех материальных точек системы
всех материальных точек системы
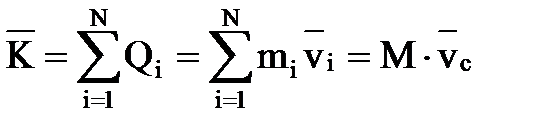 ,
,
где mi - масса i-ой точки системы;
 - вектор скорости i-ой точки системы;
- вектор скорости i-ой точки системы;
N – количество материальных точек системы;
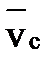 - вектор скорости центра масс системы.
- вектор скорости центра масс системы.
Если  = 0 , то
= 0 , то  , т.е.
, т.е.  = const.
= const.
Формулировка теоремы в интегральной форме
Изменение количества движения системы за некоторый промежуток времени равно сумме импульсов, действующих на систему внешних сил за тот же промежуток времени 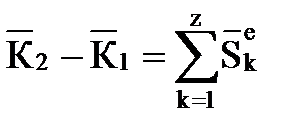
 ,
,
где 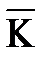 2 - количество движения системы в момент
2 - количество движения системы в момент 
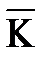 1 - количество движения системы в момент
1 - количество движения системы в момент
 - импульсы внешней силы,
- импульсы внешней силы, 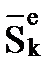 =
= 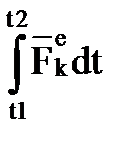
z - количество приложенных внешних сил
Теорема об изменении момента количества движения механической системы
Производная по времени от момента количества движения (кинетического момента) относительно некоторого неподвижного центра механической системы геометрически равна сумме моментов всех внешних сил системы относительно того же центра
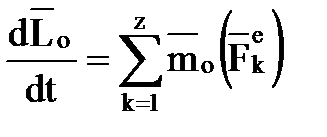 ,
,
где момент количества движения относительно данного центра (кинетический момент) 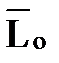 системы – вектор, равный геометрической сумме моментов количества движения
системы – вектор, равный геометрической сумме моментов количества движения 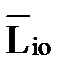 всех материальных точек системы относительно этого же центра.
всех материальных точек системы относительно этого же центра.
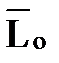 =
= 
 =
= 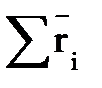 х mi
х mi 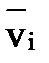 ,
,
где 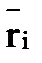 - радиус-вектор, проведенный из центра О в i-ую материальную точку системы.
- радиус-вектор, проведенный из центра О в i-ую материальную точку системы.
Если  = 0 , то
= 0 , то  0 , т.е.
0 , т.е. 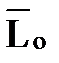 = соnst.
= соnst.
Теорема об изменении кинетической энергии механической системы
Изменение кинетической энергии механической системы при некотором ее перемещении равно сумме работ внешних сил, действующих на материальные точки системы при этом ее перемещении
Т - То = 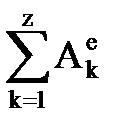 ,
,
где То - кинетическая энергия системы в начальном положении
Т - кинетическая энергия системы в конечном положении.
Кинетическая энергия Т системы - скалярная величина, равная арифметической сумме кинетических энергий всех точек системы
Т = 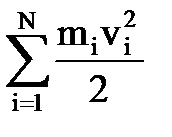
Кинетическую энергию тела можно вычислить по следующим формулам:
а) тело, движущееся поступательно, имеет кинетическую энергию
Тпост = 
б) тело, вращающееся вокруг неподвижной оси Оz , имеет кинетическую энергию Твр = 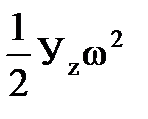
в) тело, совершающее плоское движение, имеет кинетическую
энергию
Тпл =  +
+ 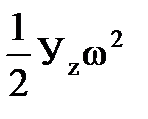 ,
,
где Уz - момент инерции тела относительно оси Оz . Осевой момент инерции вычисляем по формуле
Уz = 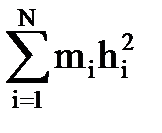 ,
,
где mi - масса i-ой точки тела;
hi - расстояние i-ой точки тела до оси Оz
или Уz = М 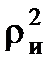 ,
,
где 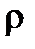 и - радиус инерции тела;
и - радиус инерции тела;
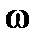 - угловая скорость вращения твердого тела.
- угловая скорость вращения твердого тела.
Моменты инерции некоторых однородных тел
1. Тонкий однородный стержень длины ℓ и массы М
Уcz =  Мℓ2
Мℓ2
2. Тонкое круглое однородное кольцо радиуса R и массы М
Уcz = MR2
3. Круглая однородная пластина или цилиндр радиуса R и массы М
Уcz =  MR2
MR2
Работа является количественной мерой превращения механического движения в какую-либо другую форму движения.
Работа силы тяжести - 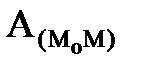 =
= 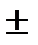 Рh ,
Рh ,
где Р - модуль силы тяжести;
h - вертикальное перемещение точки приложения силы тяжести 
Работа силы упругости - 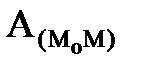 =
= 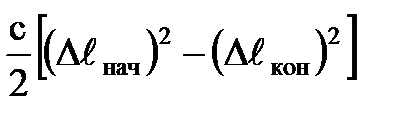 ,
,
где с - коэффициент жесткости пружины;
 - начальное удлинение пружины;
- начальное удлинение пружины;
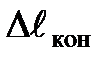 - конечное удлинение пружины.
- конечное удлинение пружины.
Работа положительна, если 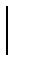

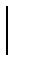 >
>  .
.
Работа постоянной силы трения - 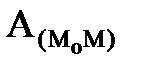 = -f ·NS ,
= -f ·NS ,
где f -  коэффициент трения;
коэффициент трения;
N - нормальная реакция опоры;
S - длина дуги кривой МоМ, по которой перемещается точка.
Работа силы трения скольжения всегда отрицательна.
Работа силы при поступательном перемещении твердого тела –
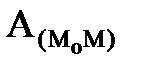 =
=  ,
,
Если 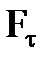 = const , то
= const , то 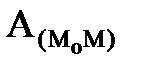 =
= 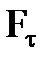 · S1 ,
· S1 ,
где 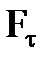 - проекция равнодействующей сил на направление перемещения;
- проекция равнодействующей сил на направление перемещения;
S1 - перемещение МоМ
Работа сил, приложенных к твердому телу, вращающемуся вокруг неподвижной оси -  ,
,
где Мz - вращающийся момент, приложенный к твердому тело;
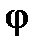 о ,
о , 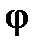 - углы поворота твердого тела в начальном и конечном его положении.
- углы поворота твердого тела в начальном и конечном его положении.
Перечень основной и дополнительной учебной литературы,
Дата добавления: 2021-05-18; просмотров: 73; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
