Первая (прямая) задача динамики
РАЗДЕЛ III. ДИНАМИКА
Динамика – раздел механики, изучающий движение материальных точек (тел) в зависимости от действующих на них сил.
Динамика делится на два подраздела:
– динамика материальной точки;
– динамика механической системы.
ЗАКОНЫ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ
Закон инерции (Закон Галилея-Ньютона)
Материальная точка сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока действие других тел не изменит это состояние:
u = const .
Первый закон характеризует стремление тела сохранить неизменной скорость своего движения или, иначе, сохранить приобретенное им ранее механическое движение. Это свойство тела называется его инертностью.
Система отсчета, для которой справедлив закон инерции, называется
инерциальной и условно считается не подвижной.
Закон пропорциональности силы и ускорения
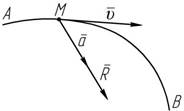Ускорение материальной точки пропор- ционально приложенной к ней силе, имеет одинаковое с ней направление и обратно пропорционально ее массе (рисунок 1.1):
Рисунок 1.1
a = R ;
m
ma = R , (1.1)
| |
где R – равнодействующая всех сил, приложенных к материальной точке, Н;
a – вектор ускорения,
m – масса, кг.
м/с2 ;
Выражение (1.1) является основным уравнением динамики.
Масса – мера инертности тела в поступательном движении. От латинского слова «inertia» – лень.
|
|
|
Если на данное тело действует сила, то обязательно должно существовать другое тело, в результате взаимодействия с которым появляется эта сила.
Величина действующих сил определяется физическими законами взаимодействия тел (законы трения, тяготения, деформации, сопротив- ления среды).
Статический эффект проявления силы – деформация. Динамический эффект проявления силы – ускорение.
1-й и 2-й законы справедливы только в инерциальной системе отсчета.
Закон равенства действия и противодействия
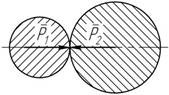Всякому действию соответствует равное и противоположно направленное противодействие:
P1 = -P2 .
Рисунок 1.2
Силы не уравновешены, так как приложены к разным телам (рисунок 1.2).
ìP1 = m1a1 ;
Þ m a
= m a
Þ a2
= m1
Þ a = a
m1 .
 |
íP = m a ,
1 1 2 2 a m
2 1 m
î 2 2 2 1 2 2
Закон независимости действия сил
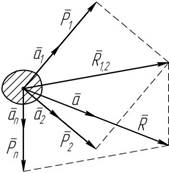Несколько одновременно действующих на материальную точку сил сообщают точке такое ускорение, какое сообщала бы ей одна сила, равная их геометрической сумме (рисунок 1.3):
|
|
|
P
n n P
1 n R
a i =i ;
a = åa i = å i =
åP i = .
Рисунок 1.3
m i=1
i=1 m m i=1 m
3-й и 4-й законы справедливы в любой системе отсчета.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ДВИЖЕНИЯ. ОСНОВНЫЕ ЗАДАЧИ ДИНАМИКИ
Пусть свободная материальная точка массой m движется по
пространственной кривой под действием сил уравнению (1.1):
P1 ,
P2 , …,
P n . Тогда согласно
d 2r
m a = åP i = R . (2.1)
Так как
a = , тогда получим дифференциальное уравнение движения
dt 2
материальной точки в векторной форме:
| |
d 2r
m dt2
= R . (2.2)
Спроецируем уравнение (2.1) на декартовы оси координат (рисунок 2.1):
d 2 x
ma x = R x ;
ma y = R y ;
d 2 y
ma z = R z .
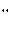d 2 z
Так как
a x =
dt2
= x ;
a y =
dt2
= y ;
a z =
dt2
= z , тогда получим
дифференциальные уравнения движения материальной точки в декартовой системе координат:
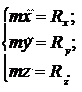(2.3)
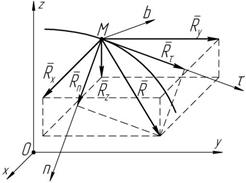Спроецируем уравнение (2.1) на естественные оси координат (рисунок 2.1):
ma t = R t ;
ma n = R n ; ma b = R b .
d u u 2
Так как
a t = dt ; a n = r ;
a b = 0 ,
Рисунок 2.1
тогда получим дифференциальные уравнения движения материальной точки в естественной системе координат:
|
|
|
ìm du = R ;
ï dt
|
|
|
ï
t
= R n ;
(2.4)
ï0 = R .
ï b
î
Первая (прямая) задача динамики
Зная массу и закон движения объекта (точка, тело, система тел)
определить модуль и направление равнодействующей сил, вызывающих это движение.
Дано: m ;
x = f1 (t );
y = f2 (t );
z = f3 (t ) .
Определить: R .
 |
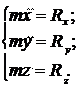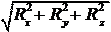
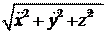R = = m .
Направление вектора R определяется направляющими косинусами:
cosa =
cosa = R x
R
;
=
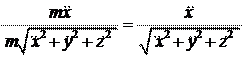cos b =
.
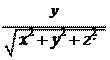
; cosg = ,
где a – угол между векторами R и
b – угол между векторами R и
g – угол между векторами R и
R x , град.;
| |
R y , град.;
 |
R z , град.
Дата добавления: 2021-05-18; просмотров: 76; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!