Сравнения с неизвестной величиной
Лекция 2
Числовые сравнения
Рассмотрим кольцо целых чисел Z = {0,± 1, ± 2, …}. Выберем m Î N, m ¹ 1 и назовем m – модулем. Введем понятие чисел, сравнимых по модулю m.
Определение. Числа a и b называют сравнимыми по модулю m, если при делении на m они дают равные остатки.
Числа сравнимые по модулю m обозначают так: a º b (mod m), читают «а сравнимо с b по модулю m».
Например: 134 º 284 (mod 10), 33 º 0 (mod 3), 12 ≢ 4 (mod 5)
При определении сравнимости двух чисел требование равноостаточности может быть заменено равносильным ему, но более удобным для проверки в конкретных случаях требованием, чтобы разность двух целых чисел делилась на модуль.
Справедливы два критерия сравнимости.
Теорема 1. Два числа сравнимы по модулю m тогда и только тогда, когда их разность делится на m, т.е. а ≡ в (mod m)  (а – в) ∶ m
(а – в) ∶ m
Доказательство.
Необходимость: а ≡ b (mod m) Þ (а – b ) ∶ m
По теореме о делении с остатком
а = m · q 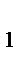 + r
+ r  , 0 £ r
, 0 £ r  < m
< m
b = m· q  + r
+ r 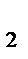 , 0 £ r
, 0 £ r 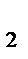 < m
< m
Т.к. а ≡ b (mod m), то r  = r
= r 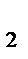 . Тогда а – b = m (q
. Тогда а – b = m (q 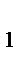 - q
- q  ). Следовательно, (а – b ) ∶ m.
). Следовательно, (а – b ) ∶ m.
Достаточность: (а- b ) ∶ m Þ а º b (mod m)
а = m q 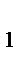 + r
+ r  0 £ r
0 £ r  < m
< m
b = m q  + r
+ r 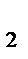 0 £ r
0 £ r 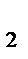 < m
< m
Следовательно, а – b = m (q 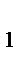 - q
- q  ) + (r
) + (r  - r
- r 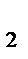 ), где – m < r
), где – m < r  - r
- r 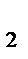 < m
< m
По условию (а – b ) ∶ m Þ [m(q 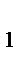 - q
- q  ) + (r
) + (r  - r
- r 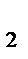 )] ∶ m Þ (r
)] ∶ m Þ (r  - r
- r 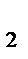 ) ∶ m Þ r
) ∶ m Þ r  - r
- r 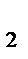 = 0 Þ r
= 0 Þ r  = r
= r 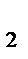 Þ а º b (mod m).
Þ а º b (mod m).
Теорема доказана.
Теорема 2. Два числа сравнимы по модулю m тогда и только тогда, когда они равны с точностью до слагаемого, кратного модулю,
|
|
|
т.е. а º в (mod m)  а = в + m × t, t Î Z.
а = в + m × t, t Î Z.
Замечание. Из теоремы о делении с остатком и второго критерия следует, что каждое целое число сравнимо по модулю m со своим остатком от деления на m.
Доказать самостоятельно!
Свойства числовых сравнений.
Пусть a, b, c и d – целые числа, m, n – натуральные числа, причем m > 1, тогда:
1. а º а (mod m) (свойство рефлексивности)
2. а º b ( mod m ) Þ b º a ( mod m ) (свойство симметричности)
3. a º b ( mod m ) и b º c ( mod m ) Þ a º c ( mod m ) (свойство транзитивности)
4. a º b ( mod m ) и с º d ( mod m ) Þ a + c º b + d ( mod m ) и а – с º b – d ( mod m )
Следствие 1. а º b (mod m) Þ a + c º b + c (mod m)
Следствие 2. a + c º b (mod m) Þ a º b – c (mod m)
5. a º b (mod m), c º d (mod m) Þ a × c º b × d (mod m)
Следствие: a º b (mod m) Þ a × c º b × с (mod m)
6. a º b (mod m) Þ a ⁿ º b ⁿ (mod m)
7. a × к º b × к (mod m × к ) Þ a º b (mod m), к Î N.
8. a × k = b × k (mod m), (m. k) = 1 Þ a º b (mod m)
9. a º b (mod m) Þ a º b + m × t (mod m), a + m × t º b (mod m), t Î Z
10. a º b (mod m 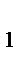 ), a º b (mod m
), a º b (mod m  ), …, a º b (mod mk) Þ
), …, a º b (mod mk) Þ
a º b ( mod М), где М = НОК ( m 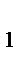 , m
, m  , … mk )
, … mk )
Следствие: если m 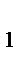 , m
, m  , …, mk попарно взаимно простые числа, т.е.
, …, mk попарно взаимно простые числа, т.е. 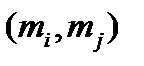 = 1 при i ¹ j, то а º b ( mod m
= 1 при i ¹ j, то а º b ( mod m 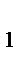 × m
× m  × …×mk ).
× …×mk ).
|
|
|
11. Пусть f (x) = an × x ⁿ + an-1 × x 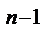 + … + a 1 × x + a 0, где a
+ … + a 1 × x + a 0, где a  Î Z и a º b (mod m) Þ
Î Z и a º b (mod m) Þ
f ( a ) º f ( b ) (mod m ).
Применение числовых сравнений
1) Нахождение остатка от деления на заданное число.
Пусть требуется найти остаток r от деления числа а на число m. По теореме о делении с остатком 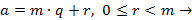 а º r (mod m).
а º r (mod m).
Значит, надо найти неотрицательное число r , меньшее m, сравнимое с 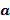 по модулю m.
по модулю m.
Пример. Найти остаток от деления числа 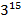 на 7.
на 7.
Решение.


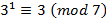 ,
, 

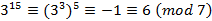 .
.  . Ответ. r=6
. Ответ. r=6
2) Нахождение нескольких последних цифр числа.
Пусть требуется найти k последних цифр числа А 
Число, составленное k последними цифрами числа А, есть остаток от деления этого числа на 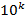 .
.
Функция Эйлера
Функция Эйлера 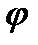 (m) выражает количество натуральных чисел, не превосходящих m и взаимно простых с m.
(m) выражает количество натуральных чисел, не превосходящих m и взаимно простых с m.
Например:
| m | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |

| 1 | 1 | 2 | 2 | 4 | 2 | 6 | 4 | 6 | 4 | 10 |
Свойства 
1) функция  - мультипликативна,
- мультипликативна,
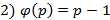 ,
,
3) 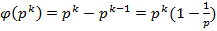 ,
,
4) 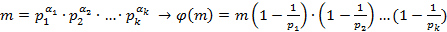 .
.
Пример: 
Классы чисел по модулю 
Из свойств 1-3 числовых сравнений следует, что отношение сравнимости по модулю  на множестве целых чисел есть бинарное отношение эквивалентности.
на множестве целых чисел есть бинарное отношение эквивалентности.
Следовательно, оно разбивает множество Z на непересекающиеся классы чисел по модулю  , объединением которых является множество Z.
, объединением которых является множество Z.
|
|
|
Пусть  =6.
=6.
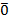
| 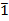
| 
| 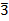
| 
| 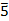
|
| 0, 6, -6, 12, -12, … | 1, 7, -5, 13, -11, … | 2, 8, -4, 14, -10, … | 3, 9, -3, 15, -9, … | 4, 10, -2, 16, -8, … | 5, 11, -1, 17, -7, … |
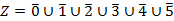 .
.
Свойства классов чисел по модулю 
1) Все числа одного класса сравнимы между собой по модулю  .
.
2) Числа разных классов не сравнимы между собой по модулю 
3) Объединением всех классов является множество Z.
4) Количество классов по модулю  равно
равно  .
.
5) Все числа одного класса по модулю m имеют с модулем один и тот же наибольший общий делитель.
Любой представитель класса по модулю  называется вычетом этого класса.
называется вычетом этого класса.
Полная система вычетов по модулю 
Определение. Полной системой вычетов по модулю  называется совокупность представителей, взятых по одному и только по одному из каждого класса чисел по модулю
называется совокупность представителей, взятых по одному и только по одному из каждого класса чисел по модулю  .
.
Пусть  =6.
=6. 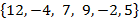 – полная система вычетов по модулю 6.
– полная система вычетов по модулю 6.
Виды полных систем вычетов по модулю  :
:
1) Полная система наименьших неотрицательных вычетов 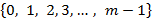
2) Полная система наименьших положительных вычетов 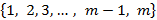
3) Полная система абсолютно наименьших вычетов: если  - четное, то
- четное, то 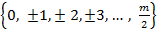 ; если
; если  -нечетное, то
-нечетное, то 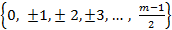 .
.
Свойства полной системы вычетов по модулю 
1) Любая совокупность  целых чисел, попарно не сравнимых по модулю
целых чисел, попарно не сравнимых по модулю  , образует полную систему вычетов по модулю
, образует полную систему вычетов по модулю  ;
;
|
|
|
2) Если (a , m)=1, b Î Z , х пробегает полную систему вычетов по модулю  , то числа вида ах+ b так же пробегают полную систему вычетов по модулю
, то числа вида ах+ b так же пробегают полную систему вычетов по модулю  .
.
Приведенная система вычетов по модулю 
Определение. Приведенной системой вычетов по модулю  называется совокупность представителей, взятых по одному и только по одному из каждого класса чисел по модулю
называется совокупность представителей, взятых по одному и только по одному из каждого класса чисел по модулю  , взаимно простых с m.
, взаимно простых с m.
Пусть  =6.
=6.  – приведенная система вычетов по модулю 6.
– приведенная система вычетов по модулю 6.
Свойства приведенной системы вычетов по модулю 
1) Если (a , m)=1, х пробегает приведенную систему вычетов по модулю  , то числа вида ах так же пробегают приведенную систему вычетов по модулю
, то числа вида ах так же пробегают приведенную систему вычетов по модулю 
2) Количество чисел в приведенной системе вычетов по модулю  равно
равно  .
.
Теоремы Эйлера и Ферма
Теорема Эйлера.
При m > 1 и (а,m) = 1 имеет место сравнение a  º 1 (mod m), где j (m) – функция Эйлера.
º 1 (mod m), где j (m) – функция Эйлера.
Доказательство:
Пусть числа а и m взаимно простые и пусть
{r1, r2, … 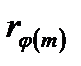 } (1)
} (1)
- любая приведенная система вычетов по модулю m. В силу свойства приведенной системы вычетов
{ar 1 , a r2, …, 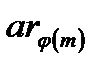 } (2)
} (2)
также представляют собой приведенную систему вычетов по модулю m. Таким образом, каждое из чисел приведенной системы вычетов (2) сравнимо по модулю m с одним из чисел приведенной системы вычетов (1), т.е.
аr 1 ≡ 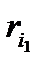
ar 2 ≡ 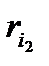 (mod m),
(mod m),
………
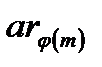 ≡
≡ 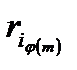
где ряд индексов i 1 , i 2 , …, 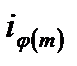 есть расположенный только в другом порядке ряд чисел 1,2,…,
есть расположенный только в другом порядке ряд чисел 1,2,…,  (m). Перемножая эти сравнения почленно, мы находим
(m). Перемножая эти сравнения почленно, мы находим
а 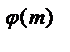 r 1 r2 …
r 1 r2 … 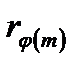 ≡
≡  …
…  ≡ r1 r2 …
≡ r1 r2 …  (mod m)
(mod m)
Так как каждое r i взаимно просто с m, то и произведение их взаимно просто с m, и, следовательно, мы можем разделить на это произведение обе части последнего сравнения. В результате получим,
а 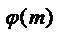 º 1 (mod m)
º 1 (mod m)
Теорема Ферма. При простом р и а не делящемся на р, справедливо сравнение
а p -1 º 1 (mod р)
Следствие. При простом р и любом натуральном а, справедливо сравнение
а p º а (mod р)
Пример. Найдите две последние цифры числа  .
.
Решение.
Число, составленное 2 последними цифрами числа, есть остаток от деления этого числа на  .
.
Значит, надо найти число r , удовлетворяющее условиям
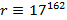 (mod 100),
(mod 100), 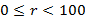 .
.
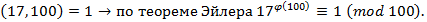
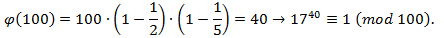
Разделим показатель степени 162 на 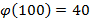 . По теореме о делении с остатком
. По теореме о делении с остатком 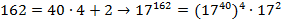 .
.
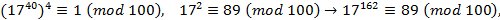
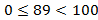 .
.
Ответ. Две последние цифры числа 8 и 9.
Сравнения с неизвестной величиной
Пусть 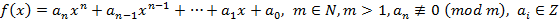 .
.
Рассмотрим сравнение 
Определение. Решением сравнения (1) называется число 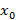 , при подстановке которого в (1) оно обращается в верное числовое сравнение.
, при подстановке которого в (1) оно обращается в верное числовое сравнение.
Теорема. Если 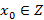 является решением сравнения (1), то и все числа, принадлежащие тому же классу вычетов по модулю
является решением сравнения (1), то и все числа, принадлежащие тому же классу вычетов по модулю  , являются решением сравнения (1).
, являются решением сравнения (1).
Таким образом, решением сравнения (1) называют класс по модулю  , состоящий из чисел, удовлетворяющих этому сравнению.
, состоящий из чисел, удовлетворяющих этому сравнению.
Для нахождения решения сравнения (1) достаточно выяснить какие классы по модулю m удовлетворяют этому сравнению, а для этого достаточно взять какое-либо число из каждого класса и проверить удовлетворяет ли оно сравнению (1). Этот метод называют «методом испытания полной системы вычетов по модулю  ».
».
Пример. Решить сравнение 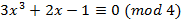 .
.
Полная система вычетов по модулю 4 имеет вид {0, 1 -1, 2}.
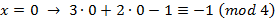
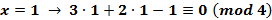
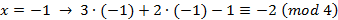

Ответ. 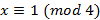
Определение. Два сравнения называются равносильными, если множества их решений совпадают.
Теоремы о равносильности сравнений с неизвестной величиной.
Т1. Если все коэффициенты в сравнении или часть из них заменить числами, сравнимыми с ними, то получим сравнение, равносильное данному.
Т2. Если к обеим частям сравнения прибавить один и тот же многочлен, то получим сравнение, равносильное данному.
Т3. Если обе части сравнения умножить или разделить на число, взаимно простое с модулем, то получим сравнение, равносильное данному.
Т4. Если обе части сравнения и модуль умножить на одно и то же натуральное число
то получим сравнение, равносильное данному.
Дата добавления: 2021-05-18; просмотров: 116; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
