Моделей распределенных программ
Формализация схемы анализа. В п. 3.1 и п. 3.2 данного раздела проблема реализуемости недетерминированной модели потоковых вычислений сводится к поиску стационарной и неизбыточной разметки М-сети на верхней полуструктуре ее свойств, не убывающих в процессе решения задачи разметки. Стационарной разметки может и не существовать. Достигнутая стационарная разметка охватывает все допустимые истории процессов, обусловленные информационной структурой программы. М-сеть адекватно представляет особенности недетерминизма потоковых моделей программ в условиях распределенности процессов, которые обмениваются разнородными сообщениями.
Теперь обобщим задачу анализа следующим образом. Объектом анализа будет маркированный потоковый граф с метками дуг и вершин, вид (семантику) которых мы не конкретизируем. Заметим, что в вводном разделе п. 3.1, посвященном основным понятиям разметки и анализа, мы не определяли точно, что представляет собой информация на входе  и выходе
и выходе 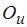 вершины
вершины 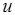 графа и каковы параметры
графа и каковы параметры 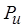 ,
, 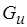 . Далее, положим, что допускаются произвольные функции приведения свойств по входам и выходам, а также функции разметки входов и выходов, т.е. их конкретный вид не задается и не предъявляется требование монотонности, как это было в случае анализа М-сетей. Из прежней постановки задачи сохраним лишь правила
. Далее, положим, что допускаются произвольные функции приведения свойств по входам и выходам, а также функции разметки входов и выходов, т.е. их конкретный вид не задается и не предъявляется требование монотонности, как это было в случае анализа М-сетей. Из прежней постановки задачи сохраним лишь правила 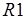 ,
, 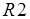 разметки, которые допускают обобщение для произвольных меток и будем считать, что заданы верхние полуструктуры меток дуг и вершин (см. п. 3.1). Возникает следующий вопрос. Можно ли в таких условиях в результате анализа обобщенного маркированного потокового графа установить, достижима ли стационарная разметка?
разметки, которые допускают обобщение для произвольных меток и будем считать, что заданы верхние полуструктуры меток дуг и вершин (см. п. 3.1). Возникает следующий вопрос. Можно ли в таких условиях в результате анализа обобщенного маркированного потокового графа установить, достижима ли стационарная разметка?
|
|
|
Здесь мы сталкиваемся с проблемой разрешимости, относящейся к так называемым массовым проблемам. Как известно, общим в постановке таких проблем является поиск ответа на вопрос, обладает ли исследуемый объект интересующим нас свойством, определяющим его принадлежность к множеству всех объектов, этим свойством обладающих. Известен ряд классических неразрешимых проблем. Это, в частности, проблемы остановки и пустой ленты в машине Тьюринга, проблема тождества слов Маркова – Поста. Так, неразрешимость проблемы остановки означает, что нельзя построить алгоритм, который устанавливал бы, остановится ли машина Тьюринга, начав работать над любым словом в заданном алфавите. Неразрешима и более частная проблема: остановится ли машина Тьюринга, работающая с пустой лентой, не содержащей никаких символов, кроме пустого. Для дальнейшего понимания этого подраздела желательным было бы предварительное знакомство с основными разделами теории алгоритмов, в частности, с рекурсивными функциями. Далее желтым цветом выделен «факультативный» материал!
|
|
|
Итак, исследование алгоритмической разрешимости задачи анализа потоковых моделей требует обобщения семантической природы меток дуг и вершин потокового графа  программы (см. п. 2.3 раздела 2), а также формализации самой схемы анализа. Цель анализа таких моделей – установление существования наименьшей верхней грани свойств дуг и вершин потокового графа
программы (см. п. 2.3 раздела 2), а также формализации самой схемы анализа. Цель анализа таких моделей – установление существования наименьшей верхней грани свойств дуг и вершин потокового графа  , которая полно, но неизбыточно представляет структурный аспект поведения программ.
, которая полно, но неизбыточно представляет структурный аспект поведения программ.
Пусть 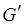 суть
суть 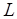 -уровневая сеть, равносильная графу
-уровневая сеть, равносильная графу  . Заданы верхние полуструктуры свойств дуг
. Заданы верхние полуструктуры свойств дуг 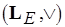 и вершин
и вершин  , функции приведения и разметки, правила
, функции приведения и разметки, правила 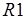 ,
, 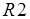 замены меток произвольной семантической природы, а также некоторая начальная разметка вершин
замены меток произвольной семантической природы, а также некоторая начальная разметка вершин 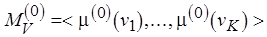 , где
, где 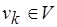 ,
, 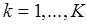 ,
,  . Задача анализа потокового графа
. Задача анализа потокового графа 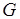 сводится к установлению существования стационарной и нахождению неизбыточной разметки сети
сводится к установлению существования стационарной и нахождению неизбыточной разметки сети 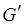 .
.
В схеме ПАСС текущая разметка 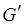 – это набор свойств ее уровней
– это набор свойств ее уровней  ,
,  , где свойство уровня
, где свойство уровня  представлено метками соответствующих вершин
представлено метками соответствующих вершин  и инцидентных им дуг. Неформально схема ПАСС представляет собой комбинацию двух проходов по уровням сети, определение свойств уровня
и инцидентных им дуг. Неформально схема ПАСС представляет собой комбинацию двух проходов по уровням сети, определение свойств уровня  по правилу
по правилу 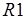 (
( 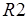 ), возвращение к уровню
), возвращение к уровню  от предшественников (преемников) и приведение свойств в
от предшественников (преемников) и приведение свойств в  -м уровне по правилу
-м уровне по правилу 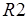 (
( 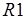 ).
).
|
|
|
Вектору  поставим в соответствие вектор натуральных чисел
поставим в соответствие вектор натуральных чисел 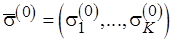 таким образом, что если
таким образом, что если 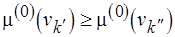 , то
, то 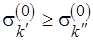 , где
, где  . Следовательно, с помощью вектора
. Следовательно, с помощью вектора 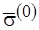 кодируются исходные свойства сети с учетом отношения частичного порядка
кодируются исходные свойства сети с учетом отношения частичного порядка 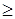 на множестве меток вершин. Каждой из начальных разметок сети, представленной набором свойств уровней, сопоставим набор частичных числовых функций
на множестве меток вершин. Каждой из начальных разметок сети, представленной набором свойств уровней, сопоставим набор частичных числовых функций 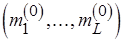 , определенных на множестве векторов
, определенных на множестве векторов 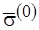 . Пусть на множестве наборов вида
. Пусть на множестве наборов вида 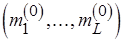 задана функция
задана функция  , любому значению которой соответствует начальная разметка
, любому значению которой соответствует начальная разметка 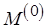 сети. Положим, нумерация уровней определяется прямой порядковой функцией
сети. Положим, нумерация уровней определяется прямой порядковой функцией 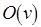 .
.
Для формального задания процедуры первого прохода от уровня 1 к уровню 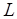 с применением правила
с применением правила 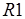 и процедуры второго прохода от уровня
и процедуры второго прохода от уровня 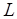 к уровню 1 с применением правила
к уровню 1 с применением правила 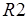 введем следующую схему примитивной рекурсии:
введем следующую схему примитивной рекурсии:
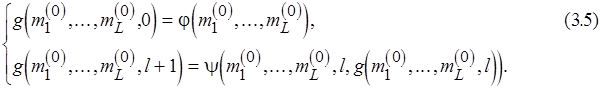
С помощью схемы (3.5) функция  получается из функций
получается из функций 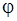 и
и 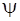 и при этом однозначно определяется последовательность изменения значений свойств уровней.
и при этом однозначно определяется последовательность изменения значений свойств уровней.
Для формального определения возвращений к уровню  от предшественников в уровнях
от предшественников в уровнях  и приведения свойств в
и приведения свойств в  -м уровне по правилу
-м уровне по правилу 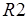 в первом проходе, а также возвращений к уровню
в первом проходе, а также возвращений к уровню  от преемников в уровнях
от преемников в уровнях 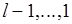 и приведения свойств уровня
и приведения свойств уровня  по правилу
по правилу 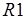 , понадобится схема возвратной рекурсии. Пусть
, понадобится схема возвратной рекурсии. Пусть  , где
, где  , являются всюду определенными функциями, причем
, являются всюду определенными функциями, причем 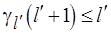 . Это – вспомогательные функции, вводимые по определению в возвратную рекурсию :
. Это – вспомогательные функции, вводимые по определению в возвратную рекурсию :
|
|
|
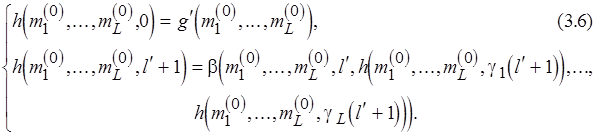
С помощью (3.6) функция  получается из функций
получается из функций 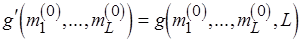 ,
,  и
и 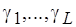 . Заметим, что при
. Заметим, что при  значение функции
значение функции  равно значению функции
равно значению функции  , полученному при
, полученному при  . Смысл (3.6) заключается в том, что "возврат" реализуется от уровня
. Смысл (3.6) заключается в том, что "возврат" реализуется от уровня  , при этом свойства уровней с меньшими номерами сохраняются, что определяется условиями
, при этом свойства уровней с меньшими номерами сохраняются, что определяется условиями  , а свойства уровней
, а свойства уровней  изменяются, т.е., строго говоря,
изменяются, т.е., строго говоря, 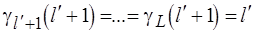 .
.
Для того чтобы схемы (3.5), (3.6) формально представляли процедуры ПАСС как при первом, так и втором проходе, достаточно следующего допущения. При первом проходе с "применением" (3.5) вводится прямая порядковая функция 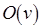 , а для (3.6) – обратная
, а для (3.6) – обратная 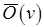 , т.е. изменяется на противоположную нумерация уровней. При втором проходе "применение" (3.5), (3.6) предполагает задание функций
, т.е. изменяется на противоположную нумерация уровней. При втором проходе "применение" (3.5), (3.6) предполагает задание функций 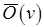 ,
, 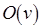 соответственно.
соответственно.
Далее, необходимо формальное представление изменяемости свойств вершин. Напомним, если они не изменяются никаким применением правил 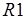 ,
, 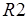 , то достигнутая разметка является стационарной. Введем функцию стационарности с помощью следующей схемы примитивной рекурсии:
, то достигнутая разметка является стационарной. Введем функцию стационарности с помощью следующей схемы примитивной рекурсии:

где 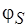 ,
, 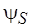 – функции, значения которых отличны от 0, если достигнутая разметка не является стационарной;
– функции, значения которых отличны от 0, если достигнутая разметка не является стационарной;  и
и 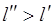 , поскольку переменная
, поскольку переменная  должна учитывать все комбинации проходов по уровням сети и возвращений.
должна учитывать все комбинации проходов по уровням сети и возвращений.
Заметим, что функция стационарности 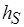 (3.7), в отличие от функций
(3.7), в отличие от функций  ,
,  в (3.5), (3.6), определяется на аргументах
в (3.5), (3.6), определяется на аргументах 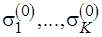 , поскольку различные свойства смежных дуг приводятся к свойству соответствующей вершины.
, поскольку различные свойства смежных дуг приводятся к свойству соответствующей вершины.
Важно, чтобы схема ПАСС была как можно "экономичнее" в смысле поиска стационарной разметки или установления факта ее недостижимости. С этой целью при помощи функции стационарности 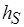 и оператора минимизации (
и оператора минимизации ( 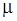 -оператора) вводится функция сложности:
-оператора) вводится функция сложности:
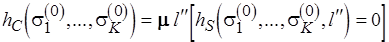 . (3.8)
. (3.8)
Уравнением (3.8) определяется наименьшее  , при котором
, при котором 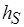 обращается в
обращается в 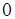 , что свидетельствует о том, что из исходных свойств сети, закодированных вектором
, что свидетельствует о том, что из исходных свойств сети, закодированных вектором 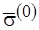 , достигнута стационарная разметка. При этом должно соблюдаться условие ее неизбыточности. Для фиксации этого факта зададим соответствующую функцию неизбыточности:
, достигнута стационарная разметка. При этом должно соблюдаться условие ее неизбыточности. Для фиксации этого факта зададим соответствующую функцию неизбыточности:
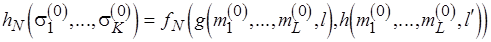 . (3.9)
. (3.9)
Функция  в (3.9) получается из функций
в (3.9) получается из функций 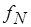 ,
,  и
и  с помощью оператора подстановки.
с помощью оператора подстановки.
Формально схемой ПАСС будем называть систему функциональных уравнений (3.5) - (3.9). При этом, если существует решение уравнений (3.7), (3.8), то функция  должна быть наименьшим из решений уравнения (3.9).
должна быть наименьшим из решений уравнения (3.9).
Интерпретация схемы анализа. Введем понятия функций и функционала, интерпретирующих формально заданную схему ПАСС (3.5) - (3.9). Обозначим через 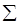 множество наборов
множество наборов 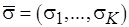 натуральных чисел, кодирующих свойства вершин на основе отношения частичного порядка, т.е.
натуральных чисел, кодирующих свойства вершин на основе отношения частичного порядка, т.е.  , где
, где 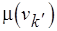 ,
, 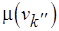 – метки вершин
– метки вершин 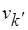 ,
, 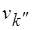 . Через
. Через 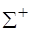 обозначим естественное расширение, включающее элемент
обозначим естественное расширение, включающее элемент 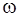 для обозначения величины не определено, т.е.
для обозначения величины не определено, т.е. 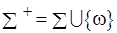 . Пусть
. Пусть  и
и 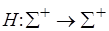 – частично определенные функции, а
– частично определенные функции, а 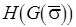 – суперпозиция
– суперпозиция 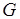 и
и 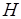 . Положим, установлено взаимно однозначное соответствие между процессом вычисления
. Положим, установлено взаимно однозначное соответствие между процессом вычисления  по (3.5) и последовательностью
по (3.5) и последовательностью
 ,
, 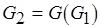 , . . . ,
, . . . , 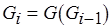 , . . . ,
, . . . ,
где 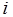 – номер шага ПАСС.
– номер шага ПАСС.
Пусть также имеет место взаимно однозначное соответствие между процессом вычисления  по (3.6) и последовательностью
по (3.6) и последовательностью
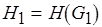 ,
, 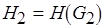 , . . . ,
, . . . , 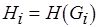 , . . .
, . . .
Тогда будем говорить, что функции 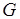 и
и 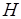 интерпретируют соответственно схемы (3.5) и (3.6) на области
интерпретируют соответственно схемы (3.5) и (3.6) на области 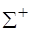 .
.
На основании результатов, изложенных в п. 3.1, можно задать функции 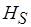 и
и 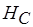 , которые интерпретируют функции стационарности
, которые интерпретируют функции стационарности 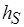 в (3.7) и сложности
в (3.7) и сложности 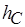 в (3.8) на подмножестве целых неотрицательных чисел, расширенном элементом
в (3.8) на подмножестве целых неотрицательных чисел, расширенном элементом 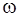 . Для установления достижимости стационарной разметки достаточно
. Для установления достижимости стационарной разметки достаточно 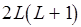 шагов ПАСС. Тогда на
шагов ПАСС. Тогда на 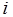 -м шаге
-м шаге

При этом
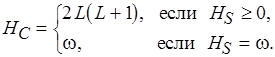
Теперь рассмотрим, как интерпретируется функция неизбыточности разметки  в уравнении (3.9). Пусть функционал
в уравнении (3.9). Пусть функционал  устанавливает соответствие между интерпретирующими функциями
устанавливает соответствие между интерпретирующими функциями 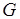 ,
, 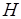 на множестве
на множестве 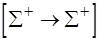 . Тем самым определяется взаимно однозначное соответствие между процессом вычисления функции
. Тем самым определяется взаимно однозначное соответствие между процессом вычисления функции 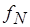 в (3.9) и последовательностью значений
в (3.9) и последовательностью значений 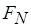 , представляющих собой суперпозиции функций
, представляющих собой суперпозиции функций 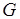 и
и 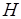 . Содержательный смысл введения функционала
. Содержательный смысл введения функционала 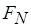 заключается в "синхронизации" вычислений
заключается в "синхронизации" вычислений  ,
,  по схемам (3.5), (3.6),
по схемам (3.5), (3.6), 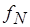 по (3.9) с последовательностями
по (3.9) с последовательностями 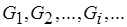 ;
; 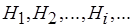 и последовательностями функций из
и последовательностями функций из 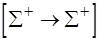 . Будем говорить, что функционал
. Будем говорить, что функционал 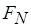 интерпретирует функцию
интерпретирует функцию 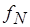 (3.9) на множестве функций
(3.9) на множестве функций 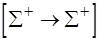 .
.
Известно, что каждая естественно расширенная функция является монотонной. Следовательно, функционал 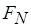 , определенный на суперпозициях монотонных функций
, определенный на суперпозициях монотонных функций 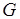 и
и 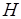 , является непрерывным. На основании первой теоремы Клини о рекурсии можно утверждать, что такой функционал имеет наименьшую неподвижную точку
, является непрерывным. На основании первой теоремы Клини о рекурсии можно утверждать, что такой функционал имеет наименьшую неподвижную точку  . Поскольку
. Поскольку 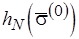 должно быть наименьшим решением уравнения (3.9), то
должно быть наименьшим решением уравнения (3.9), то 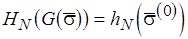 .
.
Этот результат позволяет использовать конструктивный прием для поиска стационарной неизбыточной разметки по схеме ПАСС (3.5) - (3.9) на основе определенных требований к функции, которая интерпретирует схему на множестве разметок с произвольными семантическими свойствами.
Решение задачи ПАСС. Пусть 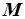 – множество разметок сети
– множество разметок сети 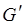 , представленных наборами свойств уровней
, представленных наборами свойств уровней 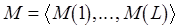 ,
, 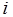 – шаг ПАСС, а
– шаг ПАСС, а  ,
, 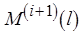 – последовательно получаемые свойства уровня
– последовательно получаемые свойства уровня  . Будем считать, что
. Будем считать, что 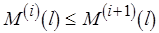 , если на
, если на 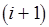 -м шаге приведенное свойство любой из вершин уровня не меньше, чем на
-м шаге приведенное свойство любой из вершин уровня не меньше, чем на 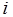 -м шаге. Если
-м шаге. Если 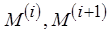 – разметки сети, представляющие совокупность свойств ее уровней, то
– разметки сети, представляющие совокупность свойств ее уровней, то  тогда и только тогда, когда
тогда и только тогда, когда 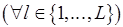
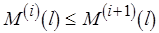 . Положим,
. Положим,  – минимальная начальная разметка. Наименьшая верхняя грань
– минимальная начальная разметка. Наименьшая верхняя грань  множества
множества 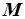 , где
, где 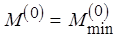 , есть неизбыточная разметка сети.
, есть неизбыточная разметка сети.
Зададим функцию разметки  , которая интерпретирует схему ПАСС на семействе свойств уровней сети
, которая интерпретирует схему ПАСС на семействе свойств уровней сети 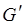 . Так, для М-сети функция
. Так, для М-сети функция 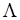 определяется конкретным видом функций приведения свойств вершин и разметки дуг (см. п. 3.1 и п. 3.2), а также порядком применения правил
определяется конкретным видом функций приведения свойств вершин и разметки дуг (см. п. 3.1 и п. 3.2), а также порядком применения правил 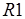 ,
, 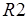 По сути, значение
По сути, значение 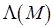 представляет собой разметку, достижимую из разметки
представляет собой разметку, достижимую из разметки  по схеме ПАСС. Любая из стационарных разметок
по схеме ПАСС. Любая из стационарных разметок 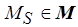 является неподвижной точкой функции разметки сети:
является неподвижной точкой функции разметки сети: 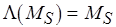 . Решением задачи ПАСС является наименьшая неподвижная точка функции
. Решением задачи ПАСС является наименьшая неподвижная точка функции  .
.
В последовательном анализе на каждом шаге изменяется свойство одного и только одного уровня. Это определяет пошаговое, поступательное и возвратно-поступательное изменение разметки сети. Продемонстрируем общий прием задания функции 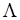 . Если уровень
. Если уровень  препятствует достижимости
препятствует достижимости 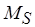 , то будем считать, что функция
, то будем считать, что функция 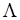 не определена на свойстве
не определена на свойстве  , и обозначать это
, и обозначать это 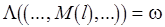 . Наоборот, если изначально задана порядковая функция
. Наоборот, если изначально задана порядковая функция 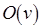 (или
(или 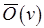 ) и уровень
) и уровень  не препятствует достижимости
не препятствует достижимости 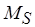 , то
, то 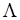 определена на уровнях
определена на уровнях 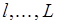 (или
(или 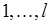 ):
):  (или
(или 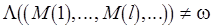 ). Построим функциональные определения свойства уровня
). Построим функциональные определения свойства уровня 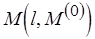 , где начальная разметка
, где начальная разметка 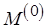 является параметром, тем самым определим и функцию разметки. Пусть изначально задана функция
является параметром, тем самым определим и функцию разметки. Пусть изначально задана функция 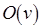 , обозначим через
, обозначим через  начальную разметку выходов сети
начальную разметку выходов сети 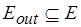 , т.е. исходящих дуг для вершин, не имеющих преемников.
, т.е. исходящих дуг для вершин, не имеющих преемников.
Введем вспомогательные функции:
 если
если 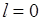 то
то 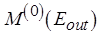 иначе
иначе  ,
,
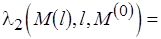 если
если 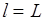 то
то 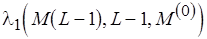 иначе
иначе 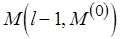 .
.
Во избежание излишней громоздкости приведем функциональные определения для поступательного изменения свойств уровней в первом проходе и возвратно-поступательного во втором. Эти определения могут быть обобщены и на случай возвращений в первом проходе. Пусть 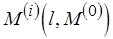 – свойство уровня
– свойство уровня  после
после 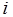 -го шага ПАСС,
-го шага ПАСС, 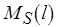 – свойство уровня, соответствующее стационарной разметке
– свойство уровня, соответствующее стационарной разметке 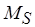 . Тогда функциональные определения имеют вид:
. Тогда функциональные определения имеют вид:
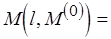 если
если 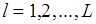 то
то
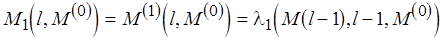
иначе 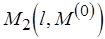 ,
,
 если
если 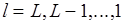 то
то 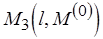
иначе 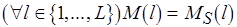 ,
,

= если 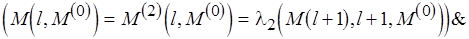
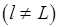
то  иначе
иначе  ,
,
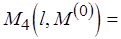 если
если 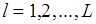 то
то  иначе
иначе 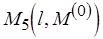 ,
,
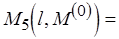
= если 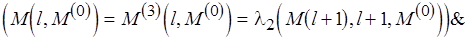
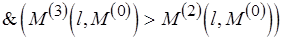 то
то 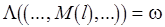
иначе  .
.
Функциональное определение  построено на результате, обсуждавшемся в п. 3.1: если при повторной переразметке уровня его свойство строго возрастает, то стационарной разметки сети не существует.
построено на результате, обсуждавшемся в п. 3.1: если при повторной переразметке уровня его свойство строго возрастает, то стационарной разметки сети не существует.
Проблема разрешимости задачи анализа. Алгоритмическая разрешимость задачи ПАСС, естественно, зависит от свойств функции разметки.
У т в е р ж д е н и е. Задача ПАСС с произвольной функцией 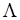 разметки сети
разметки сети 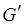 алгоритмически неразрешима.
алгоритмически неразрешима.
Приведем здесь лишь основные этапы доказательства.
Пусть 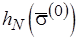 , частично рекурсивная числовая функция, представляет словарную функцию
, частично рекурсивная числовая функция, представляет словарную функцию  в нумерации
в нумерации 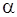 :
:
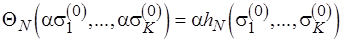 .
.
Положим, функция  задана в алфавите
задана в алфавите 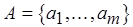 , а
, а 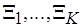 – слова в алфавите
– слова в алфавите 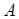 . Тогда
. Тогда  является частично рекурсивной словарной функцией.
является частично рекурсивной словарной функцией.
Согласно теореме Тьюринга для функции  существует машина Тьюринга с символами
существует машина Тьюринга с символами 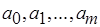 и подходящими внутренними состояниями, где
и подходящими внутренними состояниями, где 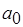 – пустое состояние, которая вычисляет функцию
– пустое состояние, которая вычисляет функцию  .
.
Таким образом, проблема остановки машины Тьюринга может быть сведена к поиску решения задачи ПАСС, которому однозначно соответствует наименьшая неподвижная точка 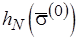 функционала
функционала 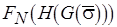 . Здесь используется так называемый метод сведения, когда известная неразрешимая проблема сводится к изучаемой. На этом основании делается вывод, что исследуемая проблема также алгоритмически неразрешима. Если бы существовало решение задачи ПАСС с произвольной функцией
. Здесь используется так называемый метод сведения, когда известная неразрешимая проблема сводится к изучаемой. На этом основании делается вывод, что исследуемая проблема также алгоритмически неразрешима. Если бы существовало решение задачи ПАСС с произвольной функцией 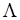 разметки, то данное сведение позволило бы решить проблему остановки машины Тьюринга, которая, как известно, является алгоритмически неразрешимой.
разметки, то данное сведение позволило бы решить проблему остановки машины Тьюринга, которая, как известно, является алгоритмически неразрешимой.
Пусть свойство любого из уровней не убывает в процессе разметки. Значит, если 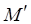 – разметка сети, достижимая из
– разметка сети, достижимая из 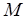 , а
, а 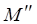 достижима из
достижима из 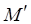 , то
, то 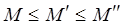 , откуда следует, что
, откуда следует, что 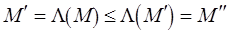 . Такая функция разметки
. Такая функция разметки 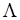 является монотонной. Так, если свойства
является монотонной. Так, если свойства 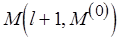 ,
, 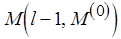 во вспомогательных функциях
во вспомогательных функциях 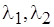 для М-сети определяются по правилам
для М-сети определяются по правилам  соответственно, то согласно вышеприведенным функциональным определениям функция
соответственно, то согласно вышеприведенным функциональным определениям функция 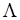 монотонна.
монотонна.
Т е о р е м а 3.2. Если функция 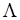 разметки монотонна, то неизбыточная разметка
разметки монотонна, то неизбыточная разметка 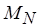 сети
сети 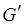 и есть решение задачи ПАСС, т.е.
и есть решение задачи ПАСС, т.е. 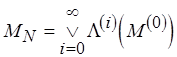 , где
, где 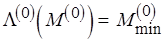 ,
,  ,
,  .
.
Д о к а з а т е л ь с т в о. Функция 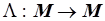 является непрерывной:
является непрерывной: 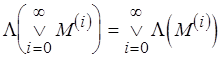 . Действительно, рассмотрим произвольную цепь
. Действительно, рассмотрим произвольную цепь 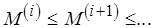 , где
, где 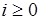 . Ясно, что для любого
. Ясно, что для любого 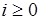
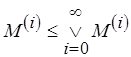 . В силу монотонности
. В силу монотонности 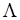 справедливо:
справедливо: 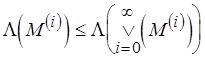 для каждого
для каждого 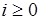 . Поэтому
. Поэтому 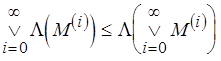 .
.
Зафиксируем некоторое значение 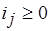 . Тогда
. Тогда

 .
.
Так как  выбиралось произвольно, то
выбиралось произвольно, то  . Отсюда и следует, что
. Отсюда и следует, что 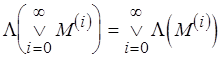 .
.
Поскольку 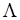 непрерывна, то на основании теоремы о неподвижной точке
непрерывна, то на основании теоремы о неподвижной точке  – наименьшая неподвижная точка. При этом
– наименьшая неподвижная точка. При этом  . Значит,
. Значит, 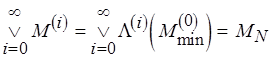 . Теорема доказана.
. Теорема доказана.
Монотонность функции 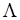 позволяет распознавать недостижимость стационарной разметки, не дожидаясь завершения прохода с возвращениями по всем уровням сети. Пусть
позволяет распознавать недостижимость стационарной разметки, не дожидаясь завершения прохода с возвращениями по всем уровням сети. Пусть 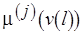 ,
, 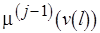 – свойства вершины
– свойства вершины 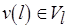 , где индекс
, где индекс 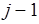 уже учитывает приведение свойств преемников или предшественников, и
уже учитывает приведение свойств преемников или предшественников, и 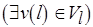
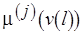
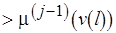 . Тогда уровень
. Тогда уровень  препятствует достижимости стационарной разметки.
препятствует достижимости стационарной разметки.
На рис. 3.9 приведен пример алгоритма распознавания существования стационарной разметки для изначально заданной порядковой функции 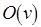 .
.
{параметры 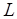 ,
,  ;
;
{для 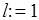 шаг1до
шаг1до 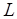 цикл
цикл 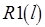 };
};
{параметры 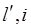 ;для
;для 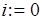 шаг1до
шаг1до 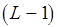 цикл
цикл 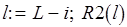 ;
;
{если  то {для
то {для 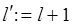 шаг1до
шаг1до 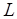 цикл
цикл 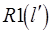 };
};
{параметр 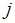 ;для
;для 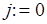 шаг1до
шаг1до 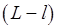 цикл
цикл 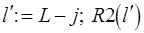 }
}
};
{если 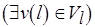
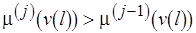 то стационарная
то стационарная
разметка не достижима иначе уровень  не препятствует
не препятствует
достижимости стационарной разметки }
}
}
Рис. 3.9. Алгоритм распознавания недостижимости стационарной разметки
На рис. 3.9 процедуры получения разметок уровня  по правилам
по правилам  обозначены
обозначены  , фигурными скобками { , } – начало, конец. При первом проходе применяется лишь правило
, фигурными скобками { , } – начало, конец. При первом проходе применяется лишь правило 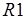 , т.е. нет необходимости возвращений к преемникам для приведения их свойств по правилу
, т.е. нет необходимости возвращений к преемникам для приведения их свойств по правилу 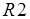 . Этот случай соответствует М-сети, все метаоператоры которой имеют одну выходную позицию (см. рис. 3.6, б).
. Этот случай соответствует М-сети, все метаоператоры которой имеют одну выходную позицию (см. рис. 3.6, б).
Таким образом, алгоритм распознавания представляет собой последовательность первого прохода от уровня 1 к уровню 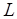 с применением правила
с применением правила 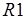 и второго прохода от уровня
и второго прохода от уровня 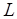 к уровню 1 с возвращениями от текущего уровня
к уровню 1 с возвращениями от текущего уровня  к уровню
к уровню 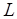 и обратно (рис. 3.10). При этом проверяется, возрастают ли приведенные свойства вершин уровня. Если нет уровней, препятствующих достижимости стационарной разметки, то она и является результатом работы алгоритма.
и обратно (рис. 3.10). При этом проверяется, возрастают ли приведенные свойства вершин уровня. Если нет уровней, препятствующих достижимости стационарной разметки, то она и является результатом работы алгоритма.
Итак, мы рассмотрели проблему алгоритмической разрешимости задачи анализа обобщенных потоковых графов программ. Уравнения (3.5) - (3.9) представляют собой формализацию схемы последовательного анализа свойств сети, соответствующей исходному графу. Функция неизбыточности разметки сети – наименьшее из решений системы функциональных уравнений, задающих схему ПАСС. Задача анализа с произвольной функцией разметки является алгоритмически неразрешимой. В случае монотонности функции разметки задача ПАСС разрешима (теорема 3.2).
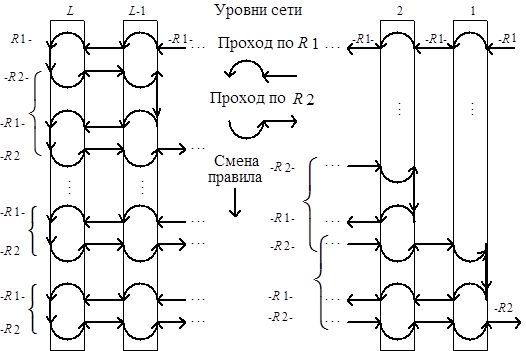
Рис. 3.10. Диаграмма проходов по алгоритму распознавания
Дата добавления: 2021-05-18; просмотров: 55; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
