Приведём другой способ построения графика.
Задание 1 № 369790
Максим страховал свою гражданскую ответственность два года. В течение второго года была сделана одна страховая выплата, но ранее выплат не было. Какой класс будет присвоен Максиму на начало третьего года страхования?
Каждый водитель в Российской Федерации должен быть застрахован по программе обязательного страхования гражданской ответственности (ОСАГО). Стоимость полиса получается умножением базового тарифа на несколько коэффициентов. Коэффициенты зависят от водительского стажа, мощности автомобиля, количества предыдущих страховых выплат и других факторов.
Коэффициент бонус-малус (КБМ) зависит от класса водителя. Это коэффициент, понижающий или повышающий стоимость полиса в зависимости от количества ДТП в предыдущий год. Сначала водителю присваивается класс 3. Срок действия полиса, как правило, один год. Каждый последующий год класс водителя рассчитывается в зависимости от числа страховых выплат в течение истекшего года, с соответствии со следующей таблицей.
| Класс на начало годового срока страхования | Коэффи-циент КБМ | Класс по окончании годового срока страхования с учётом наличия страховых случаев | ||||
| 0 страховых выплат | 1 страховая выплата | 2 страховые выплаты | 3 страховые выплаты | 4 страховые выплаты | ||
| М | 2,45 | 0 | М | М | М | М |
| 0 | 2,3 | 1 | М | М | М | М |
| 1 | 1,55 | 2 | М | М | М | М |
| 2 | 1,4 | 3 | 1 | М | М | М |
| 3 | 1 | 4 | 1 | М | М | М |
| 4 | 0,95 | 5 | 2 | 1 | М | М |
| 5 | 0,9 | 6 | 3 | 1 | М | М |
| 6 | 0,85 | 7 | 4 | 2 | М | М |
| 7 | 0,8 | 8 | 4 | 2 | М | М |
| 8 | 0,75 | 9 | 5 | 2 | М | М |
| 9 | 0,7 | 10 | 5 | 2 | 1 | М |
| 10 | 0,65 | 11 | 6 | 3 | 1 | М |
| 11 | 0,6 | 12 | 6 | 3 | 1 | М |
| 12 | 0,55 | 13 | 6 | 3 | 1 | М |
| 13 | 0,5 | 13 | 7 | 3 | 1 | М |
Решение.
|
|
|
В начале первого года Максиму был присвоен класс 3. На начало второго года ему будет присвоен класс 4, поскольку в течение первого года Максим не сделал ни одной выплаты. В течение второго года Максим сделал одну страховую выплату, значит, на начало третьего года ему будет присвоен класс 2.
Ответ: 2.
Задание 2 № 369791
Чему равен КБМ на начало третьего года страхования?
Решение.
В начале первого года Максиму был присвоен класс 3. На начало второго года ему будет присвоен класс 4, поскольку в течение первого года Максим не сделал ни одной выплаты. В течение второго года Максим сделал одну страховую выплату, значит, на начало третьего года ему будет присвоен класс 2. Следовательно, КБМ на начало третьего года страхования равен 1,4.
|
|
|
Ответ: 1,4.
Задание 3 № 369792
Коэффициент возраста и водительского стажа (КВС) также влияет на стоимость полиса (см. таблицу).
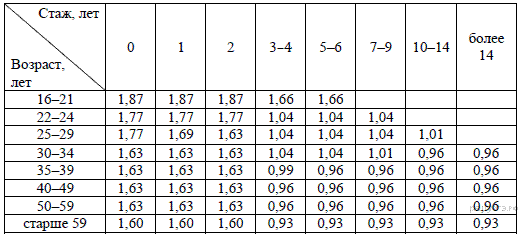
Когда Максим получил водительские права и впервые оформил полис, ему было 25 лет. Чему равен КВС на начало 3-го года страхования?
Решение.
Поскольку когда Максим впервые получил права и оформил полис ему было 25 лет, на начало 3-го года страхования он будет попадать в возрастную категорию 25−29 лет, а его стаж будет попадать в промежуток 2 года. Следовательно, КВС равен 1,63.
Ответ: 1,63.
Задание 4 № 369793
В начале второго года страхования Максим заплатил за полис 16 055 руб. Во сколько рублей обойдётся Максиму полис на третий год, если значения других коэффициентов (кроме КБМ и КВС) не изменятся?
Решение.
Найдём КБМ и КВС на начало второго года. КБМ на начало третьего года равен 0,95. КВС на начало второго года равен 1,69. Теперь найдём составим уравнение и найдём другие коэффициенты:
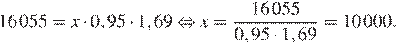
КБМ на начало третьего года равен 1,4, КВС на начало третьего года равен 1,63. Значит, на начало третьего года стоимость полиса равна
|
|
|
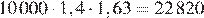 руб.
руб.
Ответ: 22 820.
Задание 5 № 369794
Максим въехал на участок дороги протяжённостью 3,4 км с камерами, отслеживающими среднюю скорость движения. Ограничение скорости на дороге — 80 км/ч. В начале и в конце участка установлены камеры, фиксирующие номер автомобиля и время проезда. По этим данным компьютер вычисляет среднюю скорость на участке. Максим въехал на участок в 10:05:23, а покинул его в 10:07:39. Нарушил ли Максим скоростной режим? Если да, на сколько км/ч средняя скорость на данном участке была выше разрешённой?
Решение.
Поскольку Максим въехал на участок в 10:05:23, а покинул его в 10:07:39, он проехал расстояние в 3,4 км за 136 секунд. Переводя в часы, получаем  ч. Значит, он двигался со средней скоростью в
ч. Значит, он двигался со средней скоростью в 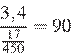 км/ч. Таким образом, Максим превысил скорость на 10 км/ч.
км/ч. Таким образом, Максим превысил скорость на 10 км/ч.
Ответ: 10.
Задание 6 № 314203
Найдите значение выражения 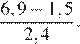
Решение.
Умножим числитель и знаменатель на 10:

Ответ: 2,25.
Задание 7 № 322449
На координатной прямой отмечены числа a и x.

Какое из следующих чисел наименьшее?
В ответе укажите номер правильного варианта.
1) 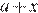
2) 
3) 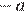
4) 
Решение.
Отметим на координатной прямой приведённые в условии числа:

|
|
|
Из рисунка видно, что наименьшим из данных чисел является a + x.
Правильный ответ указан под номером: 1.
Задание 8 № 383598
Найдите значение выражения 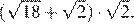
Решение.
Вычислим:
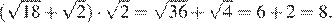
Ответ: 8.
Задание 9 № 338202
Квадратный трёхчлен разложен на множители: 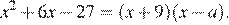 Найдите
Найдите 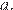
Решение.
Корни уравнения 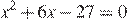 — суть числа −9 и 3. В силу формулы
— суть числа −9 и 3. В силу формулы  где
где  и
и 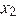 — корни уравнения
— корни уравнения 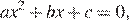 получаем
получаем  Следовательно,
Следовательно, 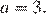
Задание 10 № 333125
Из 1500 карт памяти, поступивших в продажу, в среднем 30 не работают. Какова вероятность того, что случайно выбранная в магазине карта работает?
Решение.
Вероятность того, что карта памяти не работает  Поэтому вероятность того, что случайно выбранная карта работает
Поэтому вероятность того, что случайно выбранная карта работает 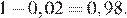
Ответ: 0,98.
Задание 11 № 339091
Установите соответствие между функциями и их графиками.
Функции
| А) y = −2x + 4 | Б) y = 2x − 4 | В) y= 2x + 4 |
Графики
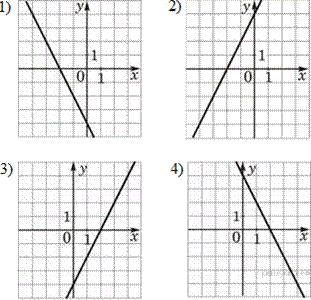
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В |
Решение.
Если прямая задана уравнением 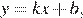 то при
то при 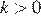 функция возрастает, при
функция возрастает, при  — убывает. Значению
— убывает. Значению 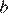 соответсвует значение функции в точке
соответсвует значение функции в точке 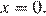
Уравнение 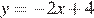 задаёт убывающую функцию, пересекающую ось ординат в точке 4.
задаёт убывающую функцию, пересекающую ось ординат в точке 4.
Уравнение 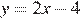 задаёт возрастающую функцию, пересекающую ось ординат в точке −4.
задаёт возрастающую функцию, пересекающую ось ординат в точке −4.
Уравнение 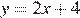 задаёт возрастающую функцию, пересекающую ось ординат в точке 4.
задаёт возрастающую функцию, пересекающую ось ординат в точке 4.
Тем самым, искомое соответствие: А — 4, Б — 3, В — 2.
Ответ: 432.
Задание 12 № 311541
Объём пирамиды вычисляют по формуле 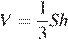 , где
, где 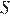 — площадь основания пирамиды,
— площадь основания пирамиды, 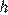 — её высота. Объём пирамиды равен 40, площадь основания 15. Чему равна высота пирамиды?
— её высота. Объём пирамиды равен 40, площадь основания 15. Чему равна высота пирамиды?
Решение.
Выразим высоту пирамиды из формулы для ее объема:
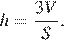
Подставляя, получаем:
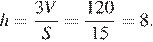
Ответ: 8.
Задание 13 № 350499
Решите неравенство 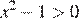
1) нет решений
2) 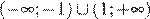
3) 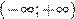
4) 
Решение.
Решим неравенство: 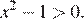 Корнями уравнения
Корнями уравнения 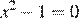 являются числа -1 и 1. Поэтому
являются числа -1 и 1. Поэтому
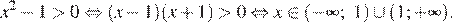
Множество решений неравенства изображено на рис. 2.
Ответ: 2
Задание 14 № 394425
Диаметры пяти шкивов, насажанных на общий вал, образуют арифметическую прогрессию. Сумма диаметров первого и третьего шкивов составляет 26,8 см, а второго и четвёртого — 31,6 см. Сколько сантиметров составляет диаметр наибольшего шкива?
Решение.
Введем обычные обозначения. Исходя из условия задачи, верны равенства: 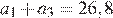 см,
см,  см. Составим и решим систему уравнений, выразив каждый член арифметической прогрессии через a1 и d:
см. Составим и решим систему уравнений, выразив каждый член арифметической прогрессии через a1 и d:

Наибольший диаметр имеет 5 шкив, найдем по формуле для 5-го члена арифметической прогрессии:
 см.
см.
Ответ: 20,6.
Задание 15 № 340106
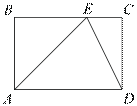
На стороне BC прямоугольника ABCD, у которого AB = 12 и AD = 17, отмечена точка E так, что ∠EAB = 45°. Найдите ED.
Решение.
Треугольник 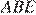 — прямоугольный, угол
— прямоугольный, угол 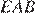 равен 45°, поскольку сумма углов треугольника равна 180°, угол
равен 45°, поскольку сумма углов треугольника равна 180°, угол 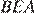 равен
равен 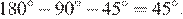 Следовательно, треугольник
Следовательно, треугольник 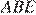 — равнобедренный, поэтому
— равнобедренный, поэтому 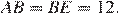 Найдём отрезок
Найдём отрезок 
 Из прямоугольного треугольника
Из прямоугольного треугольника 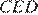 найдём
найдём 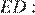
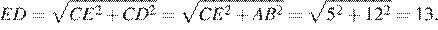
Ответ: 13.
Задание 16 № 311517

Величина центрального угла AOD равна 110°. Найдите величину вписанного угла ACB. Ответ дайте в градусах.
Решение.
Угол AOB смежный с углом AOD, поэтому AOB = 180° − 110° = 70°. Центральный угол AOB и вписанный угол ACB опираются на одну дугу. Поэтому 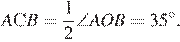
Ответ: 35.
Задание 17 № 314882

В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
Решение.

Введём обозначения, как показано на рисунке. Тогда  Треугольник
Треугольник  прямоугольный и равнобедренный, тогда высота
прямоугольный и равнобедренный, тогда высота 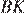 равна 3. Откуда
равна 3. Откуда 
Ответ: 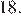
Задание 18 № 311914
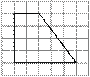
Найдите синус острого угла трапеции, изображённой на рисунке.
Решение.
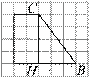
Введем обозначения, как показано на рисунке и проведём высоту трапеции СH. В прямоугольном треугольнике BCH длины катетов равны 3 и 4, поэтому гипотенуза равна  Следовательно, искомый синус острого угла B, равный отношению противолежащего углу катета CH к гипотенузе BC, равен
Следовательно, искомый синус острого угла B, равный отношению противолежащего углу катета CH к гипотенузе BC, равен 
Ответ: 0,8.
Задание 19 № 93
Укажите номера верных утверждений.
1) Существует квадрат, который не является прямоугольником.
2) Если два угла треугольника равны, то равны и противолежащие им стороны.
3) Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.
Если утверждений несколько, запишите их номера в порядке возрастания.
Решение.
Проверим каждое из утверждений.
1) «Существует квадрат, который не является прямоугольником» — некорректное утверждение, корректное — «Существует прямоугольник, который не является квадратом».
2) «Если два угла треугольника равны, то равны и противолежащие им стороны» — верно, т. к. треугольник, два угла которого равны является равнобедренным, причём равные стороны лежат напротив равных углов.
3) «Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны» — верно, это теорема планиметрии.
Ответ: 23.
Задание 20 № 338179
Решите уравнение 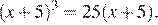
Решение.
Преобразуем уравнение:


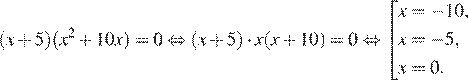
Ответ: −10; −5; 0.
Задание 21 № 338919
Первые 300 км автомобиль ехал со скоростью 60 км/ч, следующие 300 км — со скоростью 100 км/ч, а последние 300 км — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Решение.
Средняя скорость — это расстояние, разделённое на время движения. Первый отрезок пути автомобиль проехал за 300/60 = 5 часов, второй — за 300/100 = 3 часа, третий — за 300/75 = 4 часа. Средняя скорость автомобиля на протяжении всего пути составила 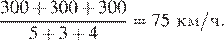
Ответ: 75.
Задание 22 № 350812
Постройте график функции  Определите, при каких значениях
Определите, при каких значениях 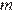 прямая
прямая  имеет с графиком ровно три общие точки.
имеет с графиком ровно три общие точки.
Решение.
Раскроем модуль. При  имеем:
имеем:
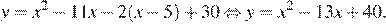
Графиком данной функции является парабола, ветви которой направлены вверх. Абсцисса вершины: 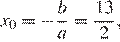 ордината вершины
ордината вершины 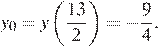 Точка пересечения графика с осью ординат:
Точка пересечения графика с осью ординат: 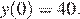 Точки пересечения с осью абсцисс найдем из уравнения
Точки пересечения с осью абсцисс найдем из уравнения  получим:
получим: 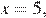
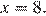 Дополнительная точка:
Дополнительная точка: 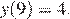
При  имеем:
имеем:
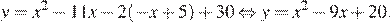
Графиком данной функции является парабола, ветви которой направлены вверх. Абсцисса вершины: 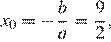 ордината вершины
ордината вершины 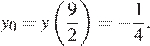 Точка пересечения графика с осью ординат:
Точка пересечения графика с осью ординат: 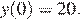 Точки пересечения с осью абсцисс найдем из уравнения
Точки пересечения с осью абсцисс найдем из уравнения 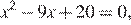 получим:
получим: 
 Дополнительная точка:
Дополнительная точка: 
График функции  изображен на рисунке.
изображен на рисунке.
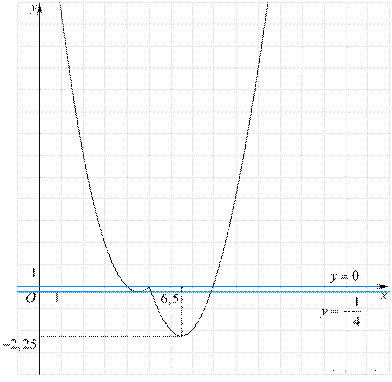
Прямая  имеет с построенным графиком ровно три общие точки при
имеет с построенным графиком ровно три общие точки при  и
и 
Ответ: 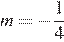 и
и 
Приведём другой способ построения графика.
Раскроем модуль:

Выделим полные квадраты:
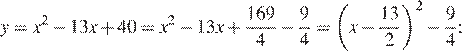

Следовательно, график функции 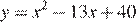 получается из графика функции
получается из графика функции 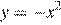 сдвигом на
сдвигом на 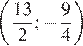 а график функции
а график функции 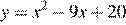 — сдвигом на
— сдвигом на 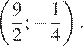
График функции  изображен на рисунке выше.
изображен на рисунке выше.
Задание 23 № 359979
Отрезки АВ и CD являются хордами окружности. Найдите длину хорды CD, если АВ = 24, а расстояние от центра окружности до хорд АВ и CD равны соответственно 16 и 12.
Решение.
 Пусть O — центр окружности, OM = 16 и ON = 12 — перпендикуляры к хордам AB и CD соответственно. По теореме Пифагора для прямоугольного треугольника OMB имеем:
Пусть O — центр окружности, OM = 16 и ON = 12 — перпендикуляры к хордам AB и CD соответственно. По теореме Пифагора для прямоугольного треугольника OMB имеем: 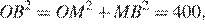 откуда ОВ = 20.
откуда ОВ = 20.
Поскольку OB = OD как радиусы окружности и MB = ON по условию, прямоугольные треугольники ОMB и OND равны по гипотенузе и катету. Следовательно, их катеты также равны: ND и OM также равны, откуда ND = 16.
Отрезок ON лежит на радиусе окружности. Радиус, перпендикулярный хорде, делит её пополам, поэтому CD = 2ND = 32.
Ответ: 32.
Задание 24 № 340387
Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке E стороны BC. Докажите, что E — середина BC.
Решение.
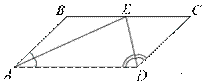
По определению параллелограмма 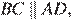
 — секущая при параллельных прямых, следовательно, углы
— секущая при параллельных прямых, следовательно, углы 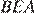 и
и 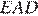 равны как накрест лежащие. Поскольку
равны как накрест лежащие. Поскольку  треугольник
треугольник 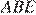 — равнобедренный, откуда
— равнобедренный, откуда  Аналогично, треугольник
Аналогично, треугольник 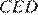 — равнобедренный и
— равнобедренный и 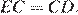 Стороны
Стороны 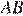 и
и 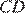 равны, как противоположные стороны параллелограмма, следовательно:
равны, как противоположные стороны параллелограмма, следовательно:
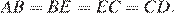 Таким образом, точка E — середина стороны
Таким образом, точка E — середина стороны 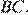
Задание 25 № 339366
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM = 10 и MB = 18. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Решение.
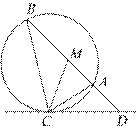
Угол ACD, образованный касательной к окружности и хордой, проведённой через точку касания, равен половине заключённой между ними дуги AC. Угол ABC — вписанный, поэтому он также равен половине дуги AC, на которую он опирается. Поэтому углы ABC и ACD равны.
В треугольниках ACD и CBD угол BDC общий, углы ABC и ACD равны. Cледовательно, эти треугольники подобны, откуда 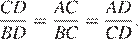
Биссектриса угла делит сторону треугольника на отрезки, пропорциональные прилежащим сторонам:  Получаем:
Получаем:
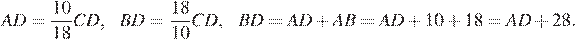
Найдём 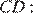


Ответ: 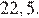
Дата добавления: 2021-04-24; просмотров: 1083; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
