Задания для самостоятельной работы
Тема: Производная и дифференциал
Производная. Понятие производной является одним из фундаментальных понятий математики. Многие задачи как самой математики, так и естествознания и техники приводят к этому понятию.
Пусть функция у= f(х) определена в промежутке X. Возьмем из этого промежутка фиксированное значение аргумента х ипридадим ему приращение Δх так, чтобы новое значение аргумента х+  х принадлежало этому промежутку. Тогда значение функции f(х) заменится новым значением f(х)+
х принадлежало этому промежутку. Тогда значение функции f(х) заменится новым значением f(х)+  у= f( x+
у= f( x+  x), т. е. функция получит приращение
x), т. е. функция получит приращение 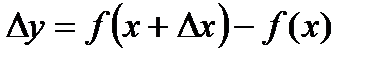 .
.
Определение. Предел отношения приращения функции  у квызвавшему его приращению аргумента
у квызвавшему его приращению аргумента  х при стремлении
х при стремлении  х к нулю, т. е.
х к нулю, т. е.
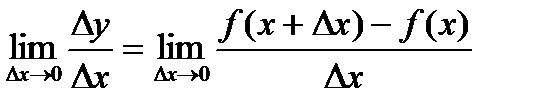 называется производной функции у= f(х) по аргументу х в точке х.
называется производной функции у= f(х) по аргументу х в точке х.
Производная обозначается одним из символов: 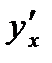 ,
, 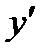 ,
, 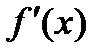 ,
,  , а ее значение при х=х0 обозначается
, а ее значение при х=х0 обозначается 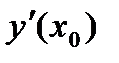 , f’(x0),
, f’(x0),  .
.
Операция нахождения производной называется дифференцированием.
Если функция f(х) имеет производную в точке х, то она называется дифференцируемой в этой точке.
Если функция f(х) имеет производную в каждой точке промежутка X, то говорят, что эта функция дифференцируема на этом промежутке.
Производная сложной функции. Пусть у= f(и), где и является не независимой переменной, а функцией независимой переменной х: и=φ(х). Таким образом, y= f(φ(х)).
В этом случае функция у называется сложной функцией х, а переменная и – промежуточным аргументом.
|
|
|
Производная сложной функции находится на основании следующей теоремы:
если y=f(u) и и=φ(х) — дифференцируемые функции своих аргументов, то производная сложной функции у=(φ(х)) существует и равна произведению производной функции у по промежуточному аргументу и на производную промежуточного аргумента и по независимой переменной х:
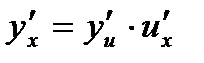
Эта теорема распространяется и на сложные функции, которые задаются с помощью цепочки, содержащей три звена и более.
Например, если у= f(и), u=φ( v), v=  , т. е y= f(φ(
, т. е y= f(φ( 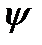 (х))), то
(х))), то 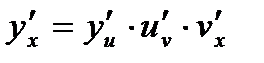 .
.
Правила дифференцирования. Во всех приведенных ниже формулах буквами и и v обозначены дифференцируемые функции независимой переменной х: и=и(х), v= v(х), а буквами а, с, п — постоянные:
1. Производная суммы (разности) равна сумме (разности) производных: 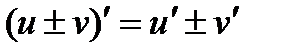 .
.
2. Производная произведения: 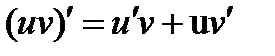 .
.
3. Постоянный множитель можно выносит за знак производной: 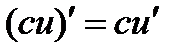 .
.
4. Производная частного: 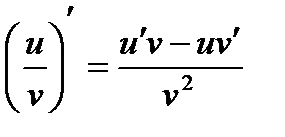 .
.
Формулы дифференцирования
5. 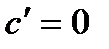 .
.
6. 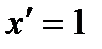 .
.
Остальные формулы записаны как для функций независимой переменной, так и для сложных функций:
7. 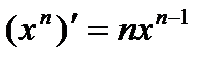 . 7а.
. 7а. 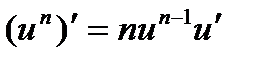 .
.
8. 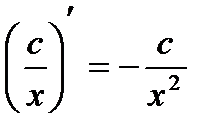 . 8а.
. 8а. 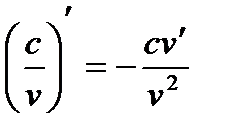 .
.
9. 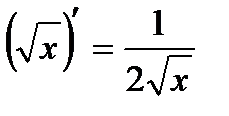 . 9а.
. 9а. 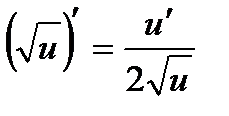 .
.
|
|
|
10. 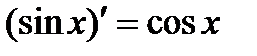 . 10а.
. 10а. 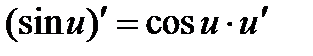 .
.
11. 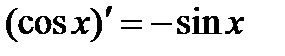 . 11а.
. 11а. 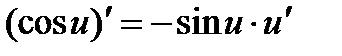
12. 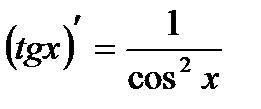 . 12а.
. 12а. 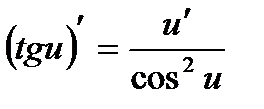 .
.
13. 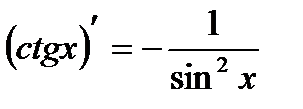 . 13а.
. 13а.  .
.
14.  . 14а.
. 14а. 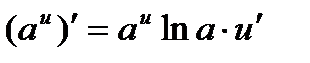 .
.
15. 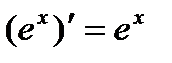 . 15a.
. 15a. 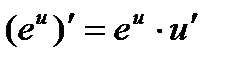 .
.
16.  16a.
16a. 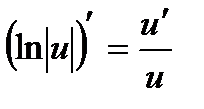 .
.
17. 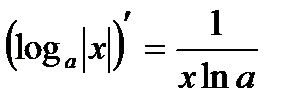 17a.
17a. 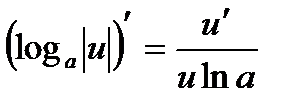 , где а > 0, а
, где а > 0, а 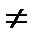 0.
0.
При решении приведенных ниже примеров сделаны подробные записи. Однако следует научиться дифференцировать без промежуточных записей.
Пример 1. Найти производную функции 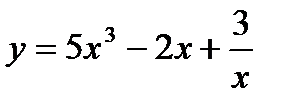
Решение. Данная функция есть алгебраическая сумма функций. Дифференцируем ее, используя формулы 1, 3, 7 и 8:
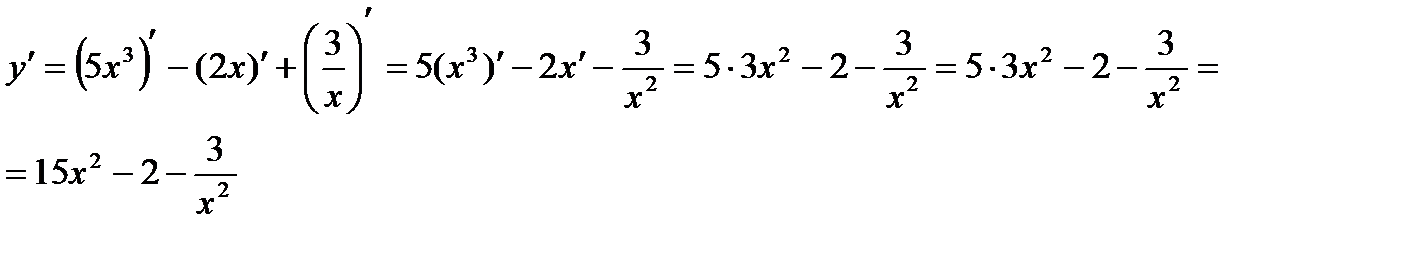
Пример 2. Найти производную функции  .
.
Решение. Применяя формулы 4, 5, 7 и 3, получим
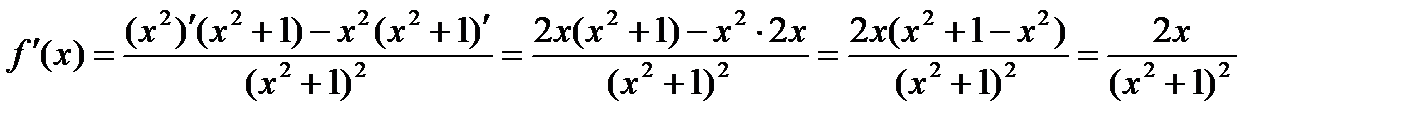 .
.
Пример 3.
Найти производную функции 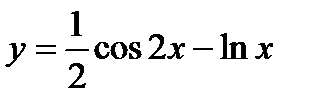 .
.
Решение.Применяя формулы 3, 5, 11а, 16, получим
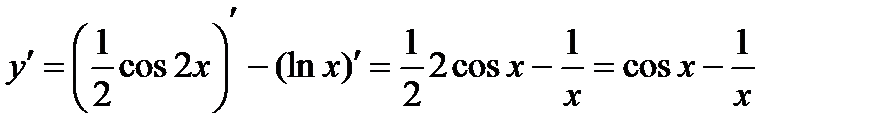 .
.
Пример 4. Найти производную функции 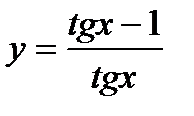
Решение. Дифференцируем данную функцию по формулам 4, 12, 5 и 3:
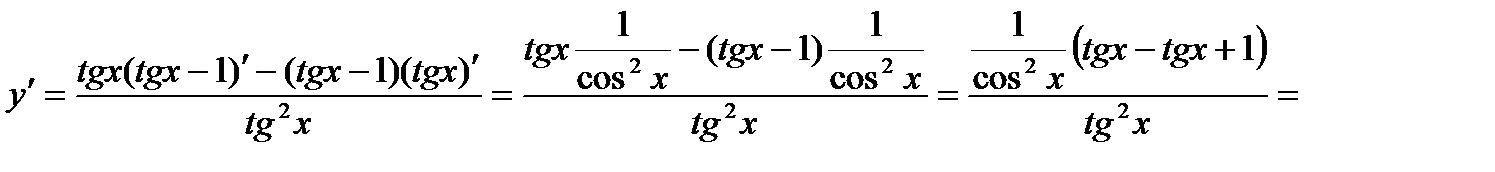
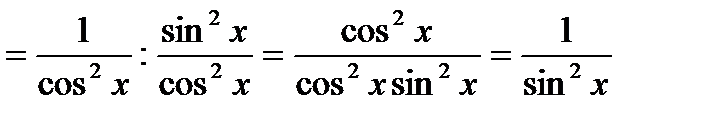 .
.
Пример 5. Найти производную функции 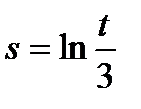 и вычислить ее значение при t=2.
и вычислить ее значение при t=2.
Решение. Дифференцируем по формулам 16а:
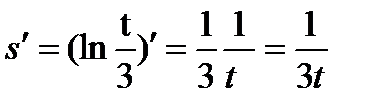 .
.
Вычислим значение производной при t=2
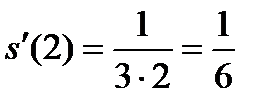 .
.
Пример 6. Найти производную функции 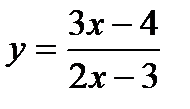 .
.
Решение.
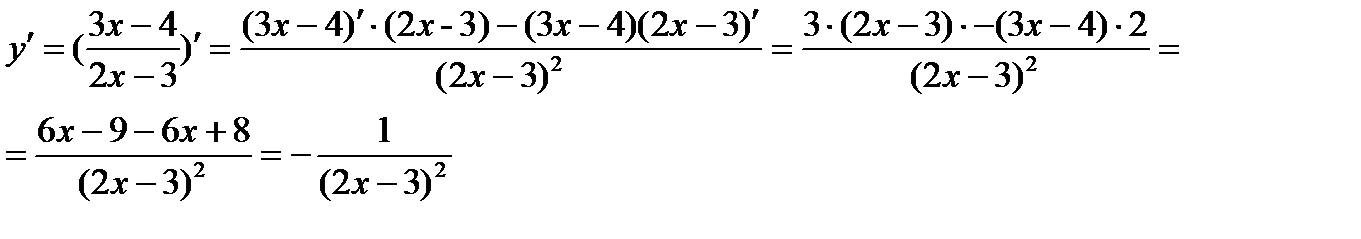
Вторая производная. Производная функции у=f(х) в общем случае является функцией от х. Если от этой функции вычислить производную, то получим производную второго порядка или вторую производную функции y=f(x).
|
|
|
Второй производной функции у=f(x) называется производная от ее первой производной у'= f'(х).
Вторая производная функции обозначается одним из символов — у", f"(х), 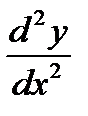 . Таким образом,
. Таким образом, 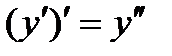 .
.
Аналогично определяются и обозначаются производные любого порядка. Например, производная третьего порядка:
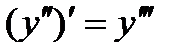 или
или 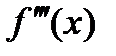 ,
, 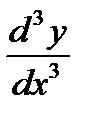 .
.
Производные высших порядков
Производная второго порядка (вторая производная) от функции 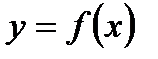 есть производная от ее первой производной:
есть производная от ее первой производной: 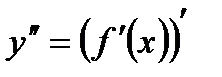 .
.
Производная третьего порядка (третья производная) от функции 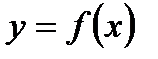 есть производная от ее второй производной:
есть производная от ее второй производной: 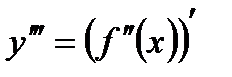 .
.
Производная n – го порядка (n – я производная) от функции 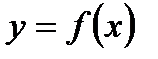 есть производная от ее (n – 1) – ой производной:
есть производная от ее (n – 1) – ой производной: 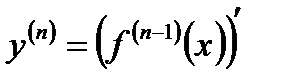 .
.
Дифференциал второго порядка (второй дифференциал) функции 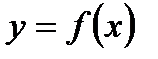 есть дифференциал от ее первого дифференциала:
есть дифференциал от ее первого дифференциала: 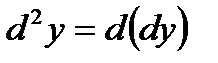 .
.
Дифференциал третьего порядка (третий дифференциал) функции 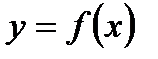 есть дифференциал от ее второго дифференциала:
есть дифференциал от ее второго дифференциала: 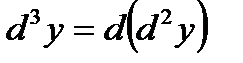 .
.
Дифференциал n – го порядка (n – ый дифференциал) функции 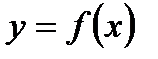 есть дифференциал от ее (n – 1) – ого дифференциала:
есть дифференциал от ее (n – 1) – ого дифференциала: 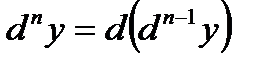 .
.
Примеры
Пример 7. Найти 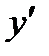 ,
,  ,
, 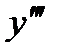 , …, если
, …, если 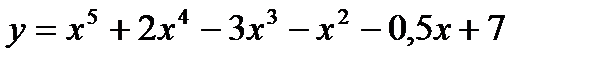 .
.
Решение: 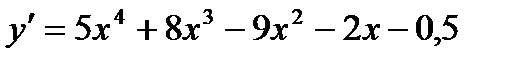 ,
,
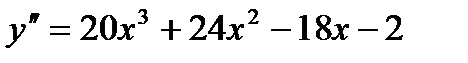 ,
,
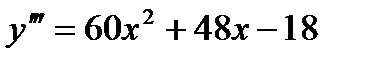 ,
,
|
|
|
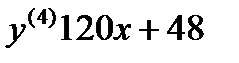 ,
, 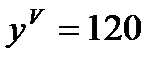 ,
, 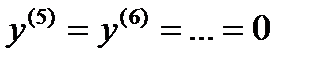 .
.
Пример 8. Найти дифференциалы первого, второго и третьего порядков функции 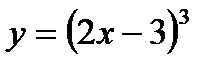 .
.
Решение: 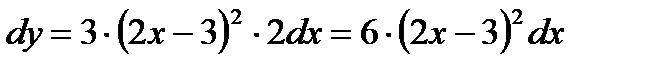 ,
,
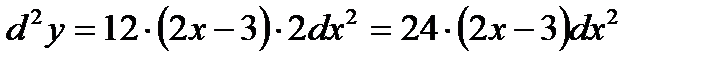 ,
,
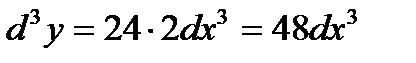 .
.
Задания для самостоятельной работы
Самостоятельная работа
Вариант 1 выполняют студенты, у которых фамилия начинается с букв Б и К,
Вариант 2 выполняют студенты, у которых фамилия начинается с буквы М,
Вариант 3 выполняют студенты, у которых фамилия начинается с букв П, Р и С,
Вариант 4 выполняют студенты, у которых фамилия начинается с букв Т, Ф, Х и К.
Дата добавления: 2021-04-24; просмотров: 317; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
