Возведение в степень и извлечение корня из комплексных чисел
Поле комплексных чисел
Комплексные числа — одна из важнейших математических абстракций, применяемая как в самой математике, так и в ее приложениях. Комплексные числа используют в реальных расчетах инженеры, физики, электронщики и другие специалисты.
В процессе изучения математики мы расширяли свои представления о числах. В начальных классах мы работали с множеством натуральных чисел N={1, 2, 3, …}, при этом их складывали, вычитали, умножали и делили. Поскольку разность двух натуральных чисел не всегда является натуральным числом, мы «расширили» множество натуральных числе до множества целых чисел Z={…, -2, -1, 0, 1, 2, 3, …}, добавив нуль и отрицательные числа. Далее, рассматривая дробные числа (частное двух целых чисел не всегда целое число), мы перешли к рациональным числам. И уже в среднем звене познакомились с понятием действительно (вещественного) числа, в связи с необходимостью введения иррациональных чисел, например, 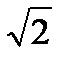 . .
| Историческая справка |
Действительные числа образуют числовое поле, т.е. числовое множество с определенными в нем операциями сложения, вычитания, умножения и деления (кроме деления на 0). Расширим поле действительных чисел, введя новое число – мнимую единицу.
При определении разрешимости квадратных уравнений мы используем дискриминант, и если дискриминант отрицателен, то обычно даем ответ: уравнение не имеет корней. Но на самом-то деле, ответ должен быть следующим: уравнение не имеет действительных корней.
|
|
|
Рассмотрим простейшее квадратное уравнение 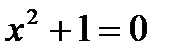 . Оно не имеет действительных корней, так как не существует действительного числа, квадрат которого был бы равен
. Оно не имеет действительных корней, так как не существует действительного числа, квадрат которого был бы равен 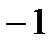 . Введем новое число, обозначив его через
. Введем новое число, обозначив его через 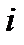 , такое, что
, такое, что 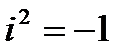 . Число
. Число 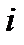 будем называть мнимой единицей (
будем называть мнимой единицей ( 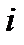 – начальная буква французского слова imaginaire – «мнимый»). Заметим, что произведение
– начальная буква французского слова imaginaire – «мнимый»). Заметим, что произведение 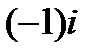 в квадрате также равно
в квадрате также равно 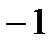 . Будем обозначать это произведение через
. Будем обозначать это произведение через 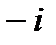 .
.
Теперь мы можем извлекать квадратные корни из любого отрицательного числа. Например, 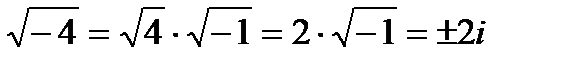 . Следовательно, мы можем найти корни квадратных уравнений вида
. Следовательно, мы можем найти корни квадратных уравнений вида 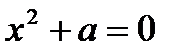 , где
, где 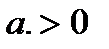 , а именно
, а именно 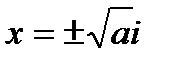 .
.
Для нахождения корней произвольного квадратного уравнения 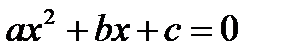 определим понятие комплексного числа.
определим понятие комплексного числа.
Введем формальное определение комплексного числа. Мы знаем, что действительные числа изображаются точками на числовой прямой:
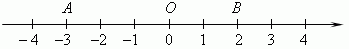
Таким образом, любой точке на этой прямой сопоставляется некоторое действительное число. Здесь, например, точке A соответствует число –3, точке B – число 2, и O – ноль.
Любой же точке на координатной плоскости соответствует пара действительных чисел. Выберем на плоскости прямоугольную (декартову) систему координат с одинаковыми масштабами на обеих осях. Упорядоченную пару действительных чисел  , соответствующую точке на этой плоскости, будем называть комплексным числом, а саму плоскость комплексной. Для комплексного числа
, соответствующую точке на этой плоскости, будем называть комплексным числом, а саму плоскость комплексной. Для комплексного числа  число a называется действительной частью числа z и обозначается Rez, b – его мнимой частью и обозначается Imz.
число a называется действительной частью числа z и обозначается Rez, b – его мнимой частью и обозначается Imz.
|
|
|
Комплексные числа, у которых действительная и мнимая части являются целыми числами, называются гауссовыми.
| Изобразить комплексное число на плоскости |
Множество всех комплексных чисел будем обозначать через C, т.е. 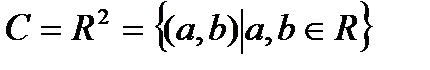 .
.
Два комплексных числа 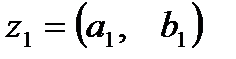 и
и 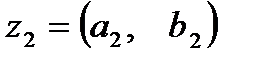 будем называть равными, если у них совпадают действительные и мнимые части:
будем называть равными, если у них совпадают действительные и мнимые части:
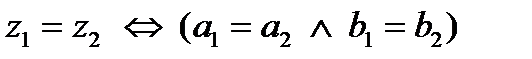
|
Пример. Пусть 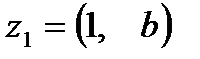 и
и 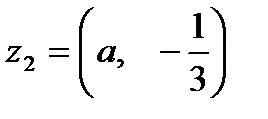 . Если
. Если 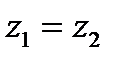 , то
, то 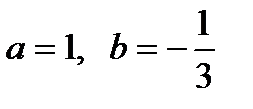 .
.
На множестве комплексных чисел введем операции сложения и умножения:
1.
| Записать правило сложения комплексных чисел |
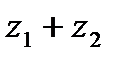 двух комплексных чисел
двух комплексных чисел 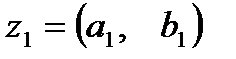 и
и 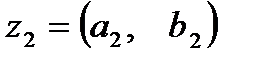 будем называть комплексное число
будем называть комплексное число  такое, что
такое, что  .
.
2.
| Записать правило умножения комплексных чисел |
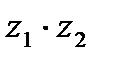 двух комплексных чисел
двух комплексных чисел 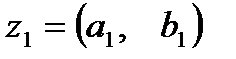 и
и 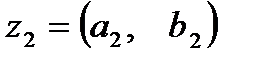 будем называть комплексное число
будем называть комплексное число  такое, что
такое, что 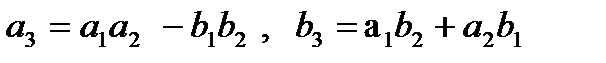 .
.
Примеры.
1) 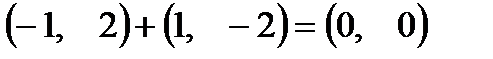 ; ;
| 2) 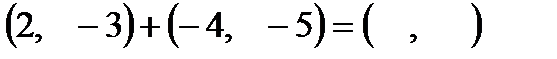 ; ;
| ||
3) 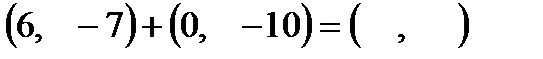 ; ;
| 4) 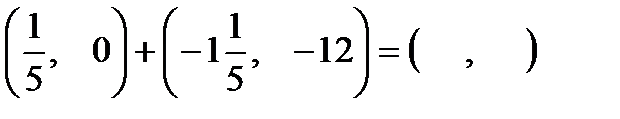 ; ;
| ||
5) 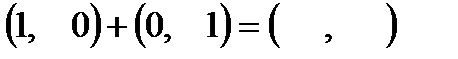 ; ;
| |||
| 6)
| |||
7) 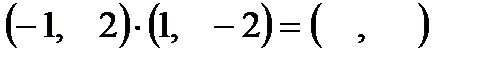 ; ;
| 8) 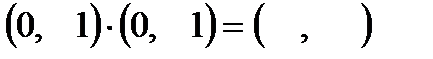 . .
| ||
| Записать свойства сложения и умножения комплексных чисел |
Перечислим свойства операций:
| 1' |
| 2' |
| 4' |
| 3' |
Вывод 1: множество комплексных чисел C относительно сложения образует коммутативную группу.
| 5' |
| 7' |
| 8' |
| 6' |
Вывод 2: множество ненулевых комплексных чисел 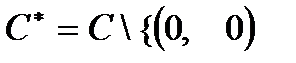 относительно умножения образует коммутативную группу.
относительно умножения образует коммутативную группу.
| Вывод 3: |
| 9' |
Рассмотрим пары 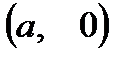 с нулевой мнимой частью. Каждой из этих пар соответствует единственное действительное число a, т.е. множество всех пар вида
с нулевой мнимой частью. Каждой из этих пар соответствует единственное действительное число a, т.е. множество всех пар вида 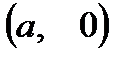 изоморфно множеству всех действительных чисел. Следовательно, всякое комплексное число
изоморфно множеству всех действительных чисел. Следовательно, всякое комплексное число 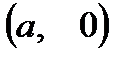 можно отождествить с действительным числом a. В частности,
можно отождествить с действительным числом a. В частности, 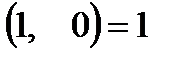 и
и 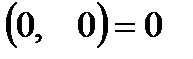 . Таким образом, можем сделать вывод, что множество действительных чисел содержится в множестве комплексных чисел. Более того, поле комплексных чисел является расширением поля действительных чисел.
. Таким образом, можем сделать вывод, что множество действительных чисел содержится в множестве комплексных чисел. Более того, поле комплексных чисел является расширением поля действительных чисел.
Вернемся к примеру, в котором мы находили квадрат пары 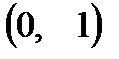 :
: 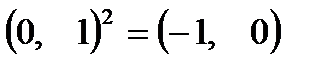 . Таким образом, мы имеем число, квадрат которого равен
. Таким образом, мы имеем число, квадрат которого равен 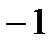 . Следовательно,
. Следовательно, 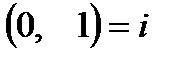 .
.
Отсюда получаем, что 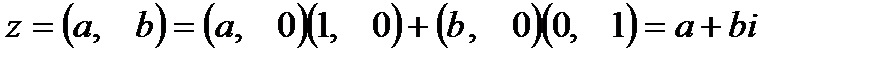 . Эта запись комплексного числа называется алгебраической.
. Эта запись комплексного числа называется алгебраической.
|
|
|
Если действительная часть комплексного числа 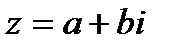 равна нулю (a = 0), то комплексное число bi называется чисто мнимым. Если b = 0 , то комплексное число
равна нулю (a = 0), то комплексное число bi называется чисто мнимым. Если b = 0 , то комплексное число 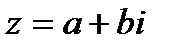 равно a и оно будет действительным числом. Если a = 0 и b = 0 одновременно, то комплексное число 0 + 0i равно нулю.
равно a и оно будет действительным числом. Если a = 0 и b = 0 одновременно, то комплексное число 0 + 0i равно нулю.
Отметим, что производить действия над комплексными числами проще в алгебраической записи. Действительно, если даны два комплексных числа 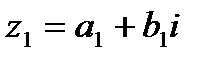 и
и 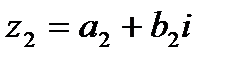 , то
, то

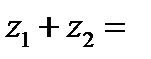
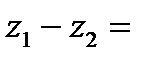
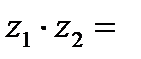

|
| Записать формулы |
Примеры.
1) 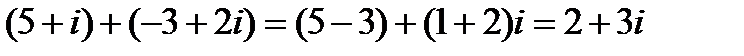 ;
;
2) 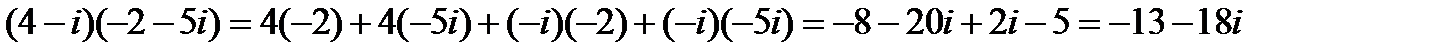 ;
;
3)
| Вычислить |
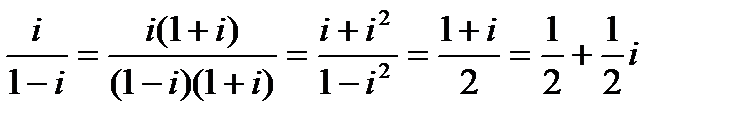 ;
;
4) 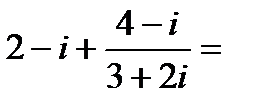
Рассмотрим геометрический смысл сложения и умножения комплексных чисел.
Пусть даны два числа 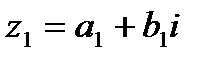 и
и 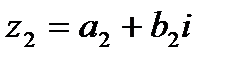 . Согласно формальному определению, комплексное число есть пара действительных чисел
. Согласно формальному определению, комплексное число есть пара действительных чисел 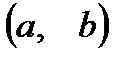 . Тогда, с точки зрения геометрии, эта пара задает на плоскости вектор с координатами
. Тогда, с точки зрения геометрии, эта пара задает на плоскости вектор с координатами 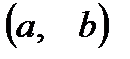 , имеющий начало в точке O – начале координат. Следовательно, наши числа
, имеющий начало в точке O – начале координат. Следовательно, наши числа 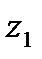 и
и 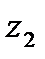 задают два вектора с координатами
задают два вектора с координатами 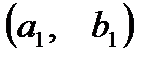 и
и 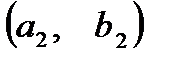 соответственно. Складывая по правилу, определенному выше, получим, что сумме
соответственно. Складывая по правилу, определенному выше, получим, что сумме 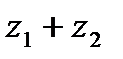 соответствует вектор с координатами
соответствует вектор с координатами 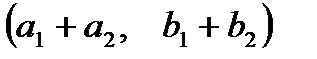 – вектор, получающийся по правилу параллелограмма. Таким образом, сложение комплексных чисел геометрически выполняется по правилу параллелограмма. Далее, число, противоположное числу
– вектор, получающийся по правилу параллелограмма. Таким образом, сложение комплексных чисел геометрически выполняется по правилу параллелограмма. Далее, число, противоположное числу 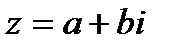 , будет точкой комплексной плоскости, симметричной с точкой z относительно начала координат (рис. 2). Отсюда без труда может быть получено геометрическое истолкование вычитания.
, будет точкой комплексной плоскости, симметричной с точкой z относительно начала координат (рис. 2). Отсюда без труда может быть получено геометрическое истолкование вычитания.
U AQAACwAAAAAAAAAAAAAAAAAvAQAAX3JlbHMvLnJlbHNQSwECLQAUAAYACAAAACEABUFyrdMHAABe NwAADgAAAAAAAAAAAAAAAAAuAgAAZHJzL2Uyb0RvYy54bWxQSwECLQAUAAYACAAAACEA7O8ig+AA AAALAQAADwAAAAAAAAAAAAAAAAAtCgAAZHJzL2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA8wAAADoL AAAAAA== ">
| Imz |
| Rez |
| z |
| –z |
| –a |
| a |
| b |
| –b |
| b2 |
| b1 |
| a2 |
| a1 |
| O |
| z1+z2 |
| z2 |
| z1 |
| Rez |
| Imz |
| Добавить пометки |
рис. 1 рис. 2
| рис.3 |
| Изобразить разность двух комплексных чисел |
Геометрический смысл умножения и деления комплексных чисел станет ясным лишь после того, как мы введем для комплексных чисел новую запись, отличную от алгебраической. Запись числа z в виде 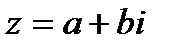 использует декартовы координаты вектора, соответствующего этому числу. Зададим этот вектор в его полярных координат: длина вектора r и угла j между положительным направлением оси абсцисс и вектором (рис. 4).
использует декартовы координаты вектора, соответствующего этому числу. Зададим этот вектор в его полярных координат: длина вектора r и угла j между положительным направлением оси абсцисс и вектором (рис. 4).
Длина r вектора, изображающего комплексное число z на плоскости, называется модулем этого числа, и обозначается 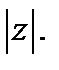 Число r является неотрицательным действительным числом, причем оно равно нулю лишь для числа 0. Для z, лежащего на действительной оси, т.е. являющегося действительным числом, число r будет абсолютной величиной z.
Число r является неотрицательным действительным числом, причем оно равно нулю лишь для числа 0. Для z, лежащего на действительной оси, т.е. являющегося действительным числом, число r будет абсолютной величиной z.
| 0 |
| z |
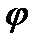
|
| r |
| Imz |
| Rez |
| b |
| a |
рис. 4
Угол j называется аргументом комплексного числа z и обозначается a rgz. Угол j может принимать любые действительные значения, как положительные, так и отрицательные, причем положительные углы должны отсчитываться против часовой стрелки. Аргумент не определен лишь для числа 0, это число вполне определяется, однако равенством 
Аргумент комплексного числа является естественным обобщением знака действительного числа. В самом деле, аргумент положительного действительного числа равен 0, аргумент отрицательного действительного числа равен p; на действительной оси из начала координат выходят лишь два направления и их можно различать двумя символами + и –, тогда как на комплексной плоскости направлений выходящих из точки 0, бесконечно много и различаются они уже углом, составляемым ими с положительным направлением действительной оси.
Между декартовыми и полярными координатами точки существует следующая связь, справедливая при любом расположении точек на плоскости:
(1)
Выразить a и b
через r и j
Отсюда
 (2)
(2)
Применим формулы (1) к произвольному комплексному числу z:
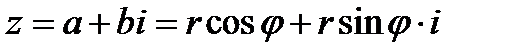 ,
,
или
 . (3)
. (3)
Обратно, пусть число 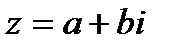 допускает запись вида
допускает запись вида 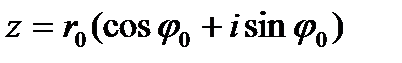 , где r0 и j 0 – некоторые действительные числа, причем r0 ³ 0. Тогда r0cos j 0 =a, r0 sin j 0 =b, откуда r0=
, где r0 и j 0 – некоторые действительные числа, причем r0 ³ 0. Тогда r0cos j 0 =a, r0 sin j 0 =b, откуда r0= 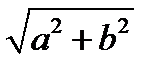 , т.е., ввиду (2),
, т.е., ввиду (2), 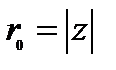 . Отсюда, используя (1), получаем: cos j 0 =cos j , sin j 0 =sin j , т.е. j 0 =argz.Таким образом, всякое комплексное число z однозначным образом записывается в виде (3), где
. Отсюда, используя (1), получаем: cos j 0 =cos j , sin j 0 =sin j , т.е. j 0 =argz.Таким образом, всякое комплексное число z однозначным образом записывается в виде (3), где 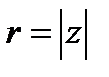 , j =argz (причем аргумент j определен лишь с точностью до слагаемых, кратных 2p). Эта запись числа z называется его тригонометрической формой, где
, j =argz (причем аргумент j определен лишь с точностью до слагаемых, кратных 2p). Эта запись числа z называется его тригонометрической формой, где  , а аргумент j вычисляется из равенств:
, а аргумент j вычисляется из равенств:
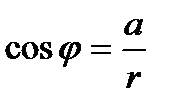 ,
, 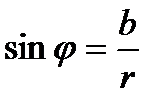 . (4)
. (4)
Выведем формулы умножения и деления комплексных чисел в тригонометрической форме. Пусть комплексные числа z1 и z2 заданы в тригонометрической форме: 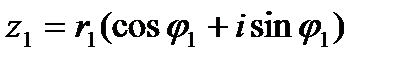 ,
, 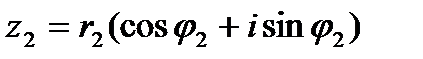 . Перемножим эти числа:
. Перемножим эти числа:
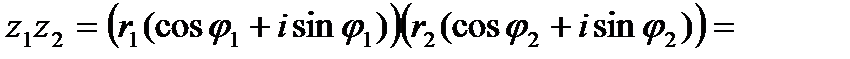
|
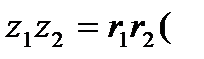
|
т.е.
(5)
Аналогично для частного, где r2 ¹ 0.
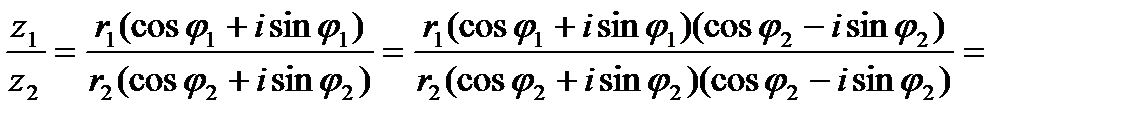
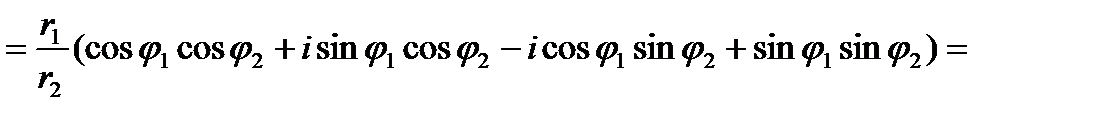
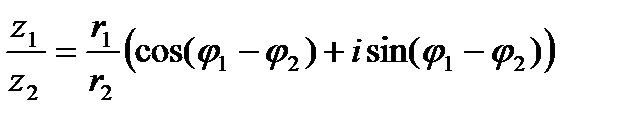 (6)
(6)
Отсюда следует, что
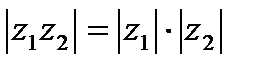 , (7)
, (7)
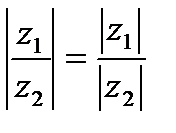 , (8)
, (8)
т.е. модуль произведения комплексных чисел равен__________________________________, модуль частного двух комплексных чисел равен _______________________________________
______________________. Далее,
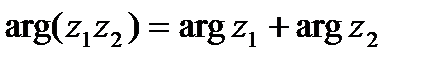 , (9)
, (9)
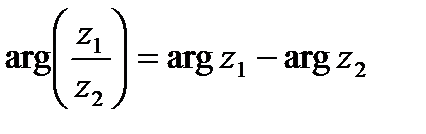 , (10)
, (10)
т.е. аргумент произведения комплексных чисел равен _______________________________, аргумент частного двух комплексных чисел получается _______________________________
___________________________________________.
Геометрический смысл умножения и деления выясняется теперь без затруднений. Действительно, ввиду формул (7) и (9), мы получим точку, изображающую произведение числа z1 на z2, если вектор, идущий от 0 к z1 (рис. 5), повернем на угол y =argz2, а затем растянем этот вектор в r2 раз. Далее, из (6) следует, что при z2¹0 будет
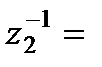 , (11)
, (11)
т.е. 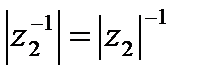 ,
, 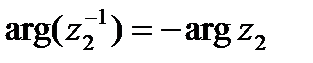 . Таким образом, мы получим точку
. Таким образом, мы получим точку 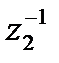 , если от точки
, если от точки 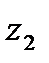 перейдем к точке
перейдем к точке 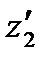 , лежащей на расстоянии
, лежащей на расстоянии 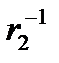 от нуля на той же полупрямой, что и точка
от нуля на той же полупрямой, что и точка 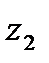 (рис. 6), а затем перейдем к точке, симметричной с
(рис. 6), а затем перейдем к точке, симметричной с 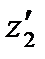 относительно действительной оси.
относительно действительной оси.
| Rez |
| z2 |
| z1 |
| Imz |
рис. 5 рис. 6
Изобразить число, обратное числу 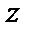 .
На рисунке показать .
На рисунке показать 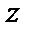 , , 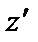 , , 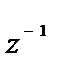
|
Замечание. Для комплексных чисел понятия "больше" и "меньше" не применяются. Для комплексных чисел введено только отношение равенства.
Возведение в степень и извлечение корня из комплексных чисел
Переходим к вопросу о возведении комплексных чисел в степень и извлечении из них корня. Для возведения числа 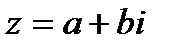 в целую положительную степень n достаточно применить к выражению
в целую положительную степень n достаточно применить к выражению  формулу бинома Ньютона, а затем воспользоваться равенствами
формулу бинома Ньютона, а затем воспользоваться равенствами 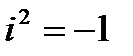 ,
,  ,
, 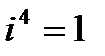 , откуда вообще
, откуда вообще
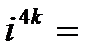 ,
, 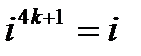 ,
, 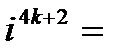 ,
, 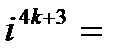 .
.
Если число z задано в тригонометрической форме, то при целом положительном n из формулы (5) вытекает следующая формула, называемая формулой Муавра:
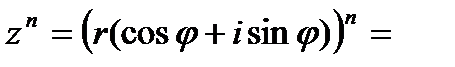
|
, (12)
т.е. при возведении комплексного числа в степень________________________________________
___________________________________ . Формула (12) верна и для целых отрицательных показателей. Действительно, ввиду 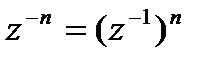 , достаточно применить формулу Муавра к числу
, достаточно применить формулу Муавра к числу 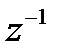 , тригонометрическую форму которого дает формула (11).
, тригонометрическую форму которого дает формула (11).
Пусть нужно извлечь корень n-ой степени из числа  . Предположим, что это сделать можно и что в результате получается число
. Предположим, что это сделать можно и что в результате получается число 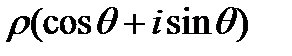 , т. е.
, т. е.
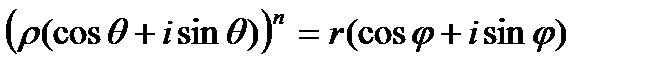 . (13)
. (13)
Тогда, по формуле Муавра, r n =r, т.е. 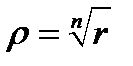 , где в правой части стоит однозначно определенное положительное значение корня n-й степени из положительного действительного числа r. С другой стороны, аргумент левой части равенства (13) есть n q . Нельзя утверждать, однако, что n q равно j , так как эти углы могут в действительности отличаться на слагаемое, являющееся некоторым целым кратным числа 2p . Поэтому n q = j +2k p , где k - целое число, откуда
, где в правой части стоит однозначно определенное положительное значение корня n-й степени из положительного действительного числа r. С другой стороны, аргумент левой части равенства (13) есть n q . Нельзя утверждать, однако, что n q равно j , так как эти углы могут в действительности отличаться на слагаемое, являющееся некоторым целым кратным числа 2p . Поэтому n q = j +2k p , где k - целое число, откуда
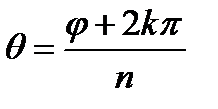 .
.
Обратно, если мы берем число 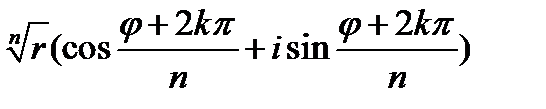 , то при любом целом k, положительном или отрицательном, n-я степень этого числа равна z. Таким образом,
, то при любом целом k, положительном или отрицательном, n-я степень этого числа равна z. Таким образом,
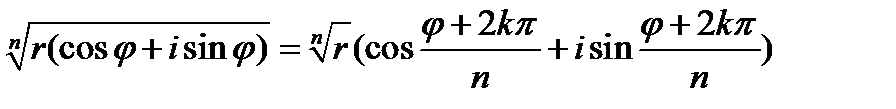 . (14)
. (14)
Давая k различные значения, мы не всегда будем получать различные значения искомого корня. Действительно, при
k=0, 1, 2, . . ., n-1 (15)
мы получим n значений корня, которые все будут различными, так как увеличение k на единицу влечет за собой увеличение аргумента на 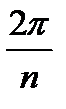 . Пусть теперь k произвольно. Если k=nq+r,
. Пусть теперь k произвольно. Если k=nq+r, 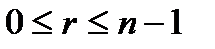 , то
, то
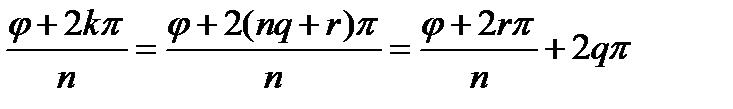 ,
,
т.е. значение аргумента при нашем k отличается от значения аргумента при r=k на число, кратное 2 p . Мы получаем, следовательно, такое же значение корня, как при значении k, равном r, т.е. входящем в систему (15).
Таким образом, извлечение корня n-ой степени из комплексного числа z всегда возможно и дает n различных значений. Все значения корня n-й степени расположены на окружности радиуса 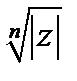 с центром в нуле и делят эту окружность на n равных частей.
с центром в нуле и делят эту окружность на n равных частей.
В частности, корень n-й из действительного числа z имеет также n различных значений; действительных среди этих значений будет два, одно или ни одного в зависимости от знака z и четности n.
Изобразить значения 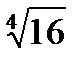 . .
|
| Imz |
| Rez |
Пример: 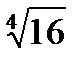 = =
|
Особенно важен случай извлечения корня n-й степени из числа 1. Этот корень имеет n значений, причем, ввиду равенства 1=cos0+isin0 и формулы (14), все эти значения или, как мы будем говорить, все корни n-й степени из единицы, задаются формулой
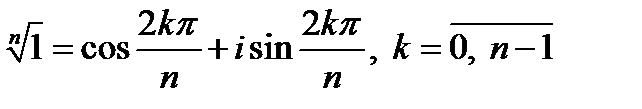 . (16)
. (16)
Обозначим множество всех корней n-й степени из числа 1 через 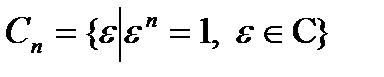 =
=
= 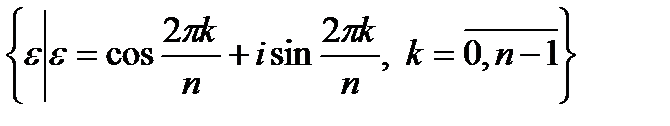 . Например,
. Например, 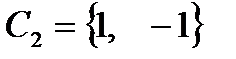 ,
, 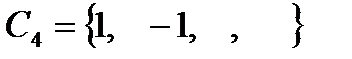 .
.
| Дописать |
Найдем кубические корни из единицы:  .
.
Следовательно,
Записать 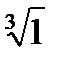 . .
|
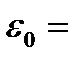
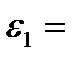
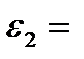
| Дописать |
Таким образом, 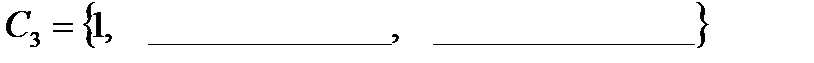 .
.
Действительные значения корня n-й степени из единицы получаются из формулы (16) при значениях k=0 и 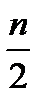 , если n четно, и при k=0, если n нечетно. На комплексной плоскости корни n-й степени из единицы расположены на окружности единичного круга и делят ее на n равных дуг; одной из точек деления служит число 1. Отсюда следует, что те из корней n-й степени из единицы, которые не являются действительными, расположены симметрично относительно действительной оси (т.е. попарно сопряжены???).
, если n четно, и при k=0, если n нечетно. На комплексной плоскости корни n-й степени из единицы расположены на окружности единичного круга и делят ее на n равных дуг; одной из точек деления служит число 1. Отсюда следует, что те из корней n-й степени из единицы, которые не являются действительными, расположены симметрично относительно действительной оси (т.е. попарно сопряжены???).
Утверждение. Все значения корня n-й степени из комплексного числа z можно получить умножением одного из этих значений на все корни n-й степени из единицы.
Доказательство. Действительно, пусть b будет одно из значений корня n-й степени из числа z, т.е. bn=z, а e - произвольное значение корня n-й степени из единицы, т.е. en =1. Тогда (be)n=bnen =z, т.е. be также будет одним из значений для 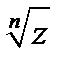 . Умножая b на каждый из корней n-й степени из единицы, мы получаем n различных значений корня n-й степени из числа z, т.е. все значения этого корня.
. Умножая b на каждый из корней n-й степени из единицы, мы получаем n различных значений корня n-й степени из числа z, т.е. все значения этого корня.
Рассмотрим свойства корней n-й степени из единицы 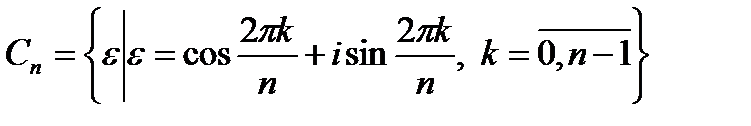 .
.
Свойство 1°Произведение двух корней n-й степени из единицы само есть корень n-й степени из единицы.
Доказательство.
Свойство 2° Умножение корней n-й степени из единицы ассоциативно.
Доказательство.
Свойство 3°Число, обратное корню n-й степени из единицы, само есть такой же корень.
Доказательство.
Вывод. Множество корней n-й степени из единицы 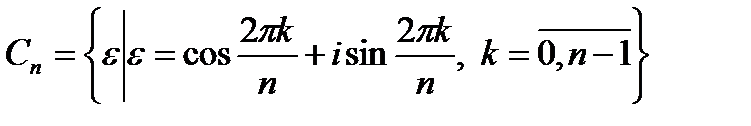 относительно умножения образует коммутативную группу.
относительно умножения образует коммутативную группу.
Свойство 4°Всякая степень корня n-й степени из единицы есть также корень n-й степени из единицы.
Доказательство.
Свойство 5°Всякий корень k-й степени из единицы будет также корнем l-й степени из единицы для всякого l, кратного k.
Доказательство.
Таким образом, некоторые из корней n-й степени из единицы, т.е. элементы 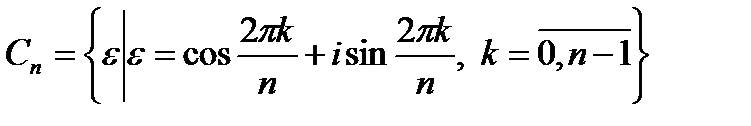 , уже будут корнями n ¢ -й степени из единицы для некоторых n ¢ , являющихся делителями числа, т.е.будут принадлежать множеству
, уже будут корнями n ¢ -й степени из единицы для некоторых n ¢ , являющихся делителями числа, т.е.будут принадлежать множеству 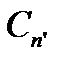 , причем n нацело делится на n ¢. Для всякого n существуют, однако, такие корни n-й степени из единицы, которые не являются корнями из единицы никакой меньшей степени. Такие корни называются первообразными корнями n-й степени из единицы. Их существование вытекает из формулы (16): если значение корня, соответствующее данному значению k, мы обозначим через ek (так что e0=1), то на основании формулы Муавра e1k=ek . Никакая степень числа e1, меньшая, чем n-я, не будет, следовательно, равна 1, т.е.
, причем n нацело делится на n ¢. Для всякого n существуют, однако, такие корни n-й степени из единицы, которые не являются корнями из единицы никакой меньшей степени. Такие корни называются первообразными корнями n-й степени из единицы. Их существование вытекает из формулы (16): если значение корня, соответствующее данному значению k, мы обозначим через ek (так что e0=1), то на основании формулы Муавра e1k=ek . Никакая степень числа e1, меньшая, чем n-я, не будет, следовательно, равна 1, т.е. 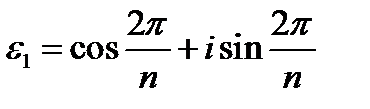 является первообразным корнем.
является первообразным корнем.
Рассмотрим свойства первообразных корней.
Теорема 1.Корень n-й степени из единицы e тогда и только тогда будет первообразным, если его степени ek, 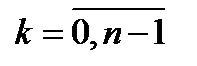 , различны, т.е. если ими исчерпываются все корни n-й степени из единицы.
, различны, т.е. если ими исчерпываются все корни n-й степени из единицы.
Доказательство. Действительно, если все указанные степени числа e различны, т.е. 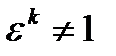 , где
, где 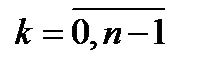 , то e будет, очевидно, первообразным корнем n-й степени. Если же, например, ek =el при 0 £ k<l £ n-1, то el-k=1, т.е., ввиду неравенств 1£ l-k £ n-1, корень e не будет первообразным.
, то e будет, очевидно, первообразным корнем n-й степени. Если же, например, ek =el при 0 £ k<l £ n-1, то el-k=1, т.е., ввиду неравенств 1£ l-k £ n-1, корень e не будет первообразным.
Число e1, найденное выше, в общем случае – не единственный первообразный корень n-й степени. Для разыскания всех этих корней служит следующая теорема.
Теорема 2.Если e есть первообразный корень n- й степени из единицы, то число ek тогда и только тогда будет первообразным корнем n-й степени, если k взаимно просто с n.
Доказательство. В самом деле, пусть d будет наибольшим общим делителем чисел k и n. Если d>1 и k=dk¢, n=dn¢, то (ek)n¢=ekn¢=ek¢n=(en)k¢=1, т.е. корень ek оказался корнем n¢-й степени из единицы.
Пусть, с другой стороны, d=1 и пусть, вместе с тем, число ek оказывается корнем m-й степени из единицы, 1£m<n. Таким образом (ek)m=ekm=1. Так как число e -первообразный корень n-й степени из единицы, т.е. лишь его степени с показателями, кратными n, могут быть равными единице, то число km будет кратным n. Отсюда вытекает, однако, так как 1£m<n, что числа k и n не могут быть взаимно простыми в противоречие с предположением.
Таким образом, число первообразных корней n-й степени из единицы равно числу целых положительных чисел k, меньших n и взаимно простых с ним.
Если p – простое число, то первообразными корнями p-й степени из единицы будут все эти корни, кроме самой единицы. С другой стороны, среди корней четвертой степени из единицы первообразными будут i и -i, но не 1 и -1.
Дата добавления: 2021-04-24; просмотров: 244; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

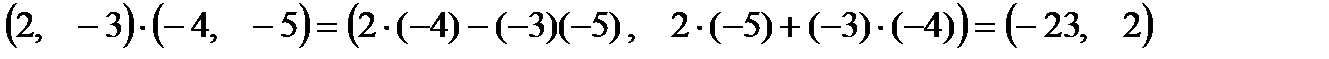 ;
;