В 19-ти случаях из 20-ти решение однородного уравнения записывают в виде общего интеграла.
Ответ: общий интеграл: 
Пример 2 Решить дифференциальное уравнение 
Решение:
Проведем стандартную замену: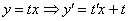 
Подставим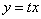 
и 
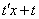в исходное уравнение: 
После подстановки результат стремимся максимально упростить:
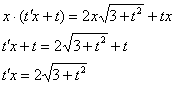Разделяем переменные и интегрируем:
Общий интеграл получен, теперь его нужно довести его до ума. Перед тем как выполнять обратную замену 
, рекомендую снова максимально упростить полученное выражение.
Упрощаем дальше:
Вот теперь обратная замена: 
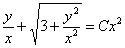
Под корнем нужно привести слагаемые к общему знаменателю и вынести из-под корня всё, что можно. Эти действия часто приходится выполнять в ходе решения однородного уравнения, запомните их:
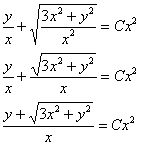Ответ: общий интеграл: 
Пример 3
Решить дифференциальное уравнение
Решение:
Для того чтобы выразить производную, нужно каждое слагаемое разделить на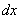 
:
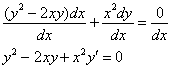Вот так-то лучше и понятнее. Проведем замену: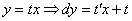 
После подстановки максимально упрощаем уравнение:
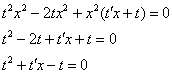Разделяем переменные:
Интегрируем: 
Используя метод неопределенных коэффициентов, разложим подынтегральную функцию в сумму элементарных дробей:
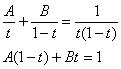
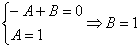
Таким образом: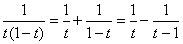 
Находим интегралы:
Перед обратной заменой в новорожденном общем интеграле опять упрощаем всё, что можно упростить:
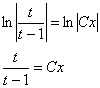Вот теперь обратная замена :
Ответ: общий интеграл: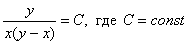 
Пример 4
Решить дифференциальное уравнение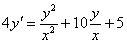 
Решение: Данное уравнение является однородным, проведем замену:
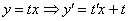
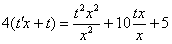После замены проводим максимальные упрощения:
|
|
|
Разделяем переменные: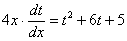 
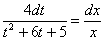Интегрируем: 
Здесь многочлен на множители раскладывается: можно решить квадратное уравнение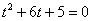 
, найти его корни и в результате: 
. Опытные студенты способны выполнить подбор корней и устно.
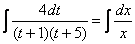Методом неопределенных коэффициентов получим сумму дробей:
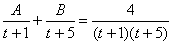
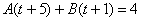
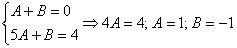Таким образом:
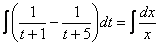
Получившийся общий интеграл упрощаем:
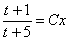
И только после упрощений выполняем обратную замену:
Ответ: общий интеграл: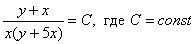 
ЧАСТЬ 3
Линейные дифференциальные уравнения первого порядка
Определение . Уравнение вида y'+ρ(x)y=f(x), где ρ(x) и f(x) непрерывные функции, называется линейным дифференциальным уравнением первого порядка.
Пример. Найти общее решение уравнения y'+3y=e2x и частное решение, удовлетворяющее начальным условиям х=0, у=1.
Решение. Данное уравнение является линейным.
Здесь ρ(x)=3 и f(x)=e2x.
Решение ищем в виде y=U∙υ, где U и υ – некоторые функции от х. Находим y'= U'υ+ Uυ' и подставляем в уравнение значение y и y', получаем: U'υ+Uυ'+3Uυ=e2 x или U'υ+U(υ'+3υ)= e2x.
Найдем одно значение υ, при котором выражение в скобках, обращается в нуль: υ'+3υ=0. Получим уравнение с разделяющимися переменными. Решая его получаем: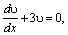 
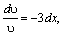ln υ =–3x,υ=e–3x.
Подставляем найденное значение υ в исходное дифференциальное уравнение, получаем уравнение с разделяющимися переменными:
.
Итак, общее решение данного уравнения имеет вид:
.
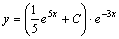Найдем частное решение. Для этого подставим начальные условия в выражение для общего решения и найдем С.
.
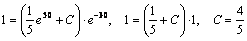Частное решение имеет вид: 
.
|
|
|
Дата добавления: 2021-04-15; просмотров: 75; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!