Тема 13.7. Преобразование алгебраических выражений
Г.
Раздел 13. Итоговое повторение курса математики
Тема 13.6. Решение дробно-рациональных уравнений
Уравнение которые можно свести к дроби: f(x)/g(x)=0 называется дробно рациональным уравнением.
Решение дробно рациональных уравнений не слишком сложная задача, если Вы знаете методику, а она достаточно проста.
Если уравнение имеет несколько слагаемых то переносим их по одну сторону знака равенства и сводим к общему знаменателю. В результате получим дробную функцию f(x)/g(x), которая равна нулю:
Следующим шагом находим корни числителя. Отвергаем среди них те, которые не принадлежат области допустимых значений (нули знаменателя) и записываем правильный ответ.
В теории все просто, однако на практике и у школьников и у студентов возникают проблемы при сведены к общему знаменателю, отыскании корней и т.д. Для ознакомления с решением рассмотрим несколько распространенных задач.
Задача 1. Найти корни уравнения:
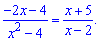
Решение: По методике переносим слагаемые и сводим к общему знаменателю:
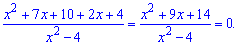
Приравниваем числитель и знаменатель к нулю и находим корни. Первое уравнение можем решить по теореме Виета:
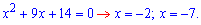
Второе раскладываем на множители:
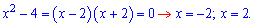
Если от корней числителя отбросить нули знаменателя то получим только одно решение x=-7.
Внимание: Всегда проверяйте совпадают ли корни числителя и знаменателя. Если такие есть то не учитывайте их в ответе.
|
|
|
Ответ: х=-7.
Задача 2. Решить уравнение:
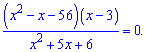
Решение: Задано дробное рациональное уравнение. Находим сначала корни числителя, для этого решаем квадратное уравнение:
Вычисляем дискриминант:
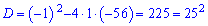
и корни уравнения:
Получили три нуля числителя:
.
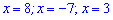Квадратное уравнение в знаменателе проще и можем решить по теореме Виета:
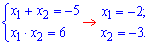
Числитель и знаменатель не имеют общих корней поэтому все три найденные значения: 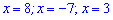будут решениями.
Ответ: х1=8; х1=-7; х1=3.
Задача 3. Найти корни уравнения:
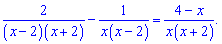
Решение: Переносим слагаемое за знак равенства:
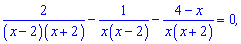
и сводим к общему знаменателю:
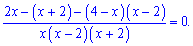
Раскрываем в числителе скобки и сводим к квадратному уравнению:
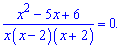
Полученное дробно рациональное уравнение эквивалентно системе двух уравнений:
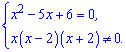
Корни первого вычисляем через дискриминант:
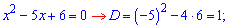
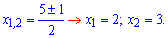
Нули второго находим без проблем:
Исключаем из решений числителя значение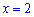 
и получим.
Ответ: х=3.
Задача 4. Пусть дано такое рациональное уравнение:
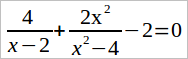
Решение: Сначала надо преобразовать левую часть уравнения, представляющую собой рациональное дробное выражение, к одной дроби. Для этого требуется найти общий знаменатель. Выражение x2 – 4 можно разложить на множители (x – 2) (x + 2). Это и будет общим знаменателем, т.к. у первой дроби выражения знаменатель (x – 2), а у третьего члена (числа –2) его вообще нет. При преобразовании дополнительным множителем к числителю первой дроби будет (x + 2), ко второй – число 1 (или отсутствие множителя), к третьей — весь знаменатель (x – 2) (x + 2). Выполним описанные действия:
|
|
|
Дробь может равняться нулю, если ее числитель равен нулю. Поэтому чтобы решить это дробное рациональное уравнение достаточно решить уравнение по отношению к числителю:
4x + 16 = 0;
x = –16 ÷ 4;
x = –4.
Если бы уравнение было квадратным, то корней могло бы быть два.
После того, как корень для числителя найден, следует проверить не обращает ли он в нуль знаменатель. Если это происходит, то найденный корень числителя не может быть корнем всего рационального уравнения. Проверяем знаменатель:
(x – 2)(x + 2) = (–4 – 2)(–4 + 2) = –6 × (–2) = 12.
При x = –4 знаменатель в нуль не обращается. Значит, корнем исходного рационального уравнения является число –4.
Ответ: х=-4.
Бывает, что рациональное выражение составляется при решении задачи. После того как корни найдены, недостаточно проверить только знаменатель на необращение его в нуль при данных корнях. Еще необходимо сопоставить корни с тем, что ищется по условию задачи. Например, если находятся количество предметов, то корень не может быть отрицательным числом.
|
|
|
Тема 13.7. Преобразование алгебраических выражений
Какие-нибудь математические выражения мы можем записать разными способами. В зависимости от наших целей, того, хватает ли нам данных и т.д. Числовые и алгебраические выражения различаются тем, что первые мы записываем только числами, объединенными с помощью знаков арифметических действий (сложение, вычитание, умножение, деление) и скобок.
Если вместо чисел ввести в выражение латинские буквы (переменные), оно станет алгебраическим. В алгебраических выражениях используются буквы, числа, знаки сложения и вычитания, умножения и деления. А также может быть использован знак корня, степени, скобки.
В любом случае, числовое это выражение или алгебраическое, оно не может быть просто случайным набором знаков, чисел и букв – в нем должен быть смысл. Это значит, что буквы, числа, знаки должны быть связаны какими-то отношениями.
Правильный пример: 7х + 2 : (у + 1).
Выше было упомянуто слово «переменная» - что оно значит? Это латинская буква, вместо которой можно подставить число. И если мы говорим о переменных, в этом случае алгебраические выражения можно назвать алгебраической функцией.
|
|
|
Переменная может принимать различные значения. И подставляя какое-то число на ее место, мы можем найти значение алгебраического выражения при этом конкретном значении переменной. Когда значение переменной другое, другим будет и значение выражения.
Дата добавления: 2021-04-05; просмотров: 55; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!