Желательный результат обсуждения.
Урок 28. Формула сложения вероятностей для трёх событий
Ранее на уроках использовались диаграммы Эйлера. Как правило, на них мы изображали два события и их комбинации. На этом уроке мы рассмотрим задачи, в которых придётся комбинировать три события.
Начните урок с отработки навыка применения диаграммы Эйлера для трёх событий.
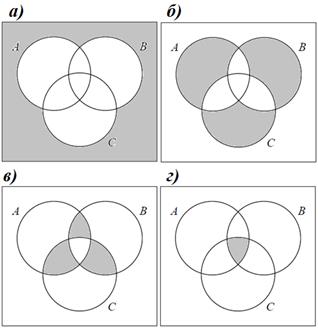
Пример 1. На диаграмме Эйлера (рис. 1) показаны события A, B и C.
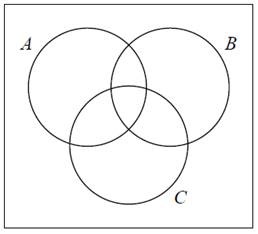
Рис. 1
Нарисуйте диаграмму в тетради и выделите на ней событие:
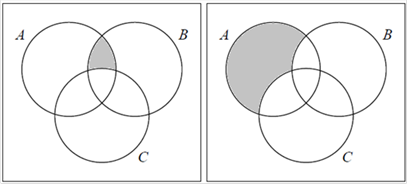
а)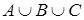 
; б) 
.
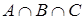Ответ:
а) б)
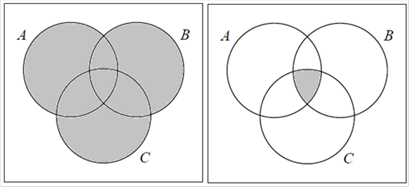
Пример 2. Нарисуйте диаграмму Эйлера для трёх событий в тетради и выделите на ней следующие события:
а) А и В одновременно наступили, но С не наступило;
б) произошло событие А, а В и С не наступили.
Запишите каждое из этих событий формулой.
Ответ:
а)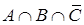 
б) 
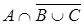или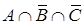 
Пример 3. Нарисуйте диаграмму в тетради и выделите на ней следующие события:
а) не наступило ни одного из трёх событий;
б) наступило ровно одно событие из трёх;
в) наступило ровно два события из трёх;
г) все три события наступили одновременно.
Ответ:
Нам известна формула сложения вероятностей для двух событий:
.
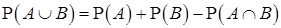Есть ли формула, позволяющая вычислять вероятность объединения трёх событий? Чтобы разобраться в этом вопросе, предложите ученикам задачу.
Пример 4. В детской языковой школе изучаются три языка: английский, немецкий и французский. Известно, что английский в ней изучают 95 детей, немецкий — 90 детей, а французский — 70 детей. Также известно, что английский и немецкий одновременно изучает 25 детей, немецкий и французский — 20 детей, а английский и французский – 15 детей. Причём, все три языка изучают 5 человек. Сколько всего детей учится в языковой школе? Какова вероятность того, что случайно выбранный ученик языковой школы изучает все три языка?
|
|
|
Решение. Условие кажется запутанным. Разобраться поможет диаграмма Эйлера. Введём обозначения: пусть событие А заключается в том, что случайный ученик школы изучает английский, событие В — немецкий, и событие С — французский.
Случайный эксперимент заключается в случайном выборе ученика. Подпишем на рисунке количество элементарных исходов, благоприятствующих событиям А, В и С (см. рис. 2).
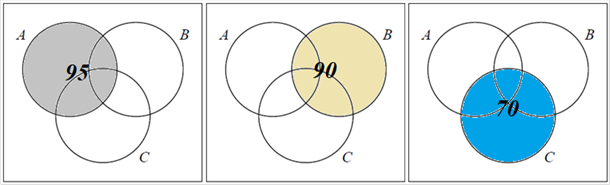
Рис. 2
Известно, сколько элементарных исходов благоприятствует событиям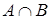 
, 
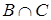и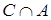 
. Укажем это на диаграмме (рис. 3).
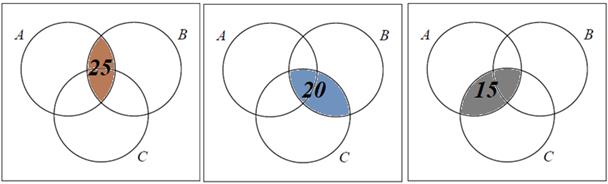
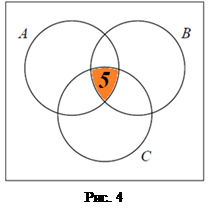Рис. 3
Все три языка изучают пятеро, то есть событию 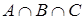благоприятствуют пять элементарных исходов (рис.4).
Обратите внимание на то, что с помощью рисунков 3 и 4 мы можем найти, сколько учеников изучает только два языка, а затем, с помощью рисунка 2, найти количество учеников, которые изучают только один язык (рис. 5).
|
|
|
Рис. 5
Теперь мы легко найдём общее количество учеников, сложив все числа на рисунке. Сумма равна 200. Следовательно, искомая вероятность равна
.
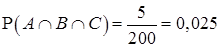Существует ли более простой способ найти количество элементарных исходов объединения трёх событий? Попробуем разобраться в этом вопросе на том же примере. Используя рисунок, посмотрим, что происходит, когда мы складываем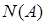 
, 
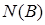и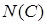 
(рис. 6).
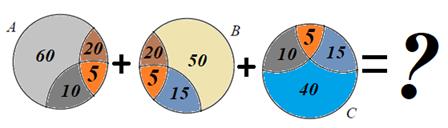
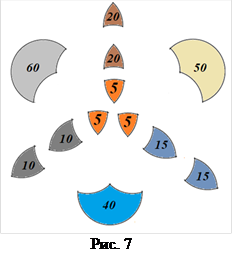Рис. 6
Обсудите с учащимися, сколько фигур каждого цвета они видят на рисунке. Обсуждение должно привести к выводу: фигуры, изображающие только одно событие, мы считаем по одному разу; фигуры, изображающие пересечение двух событий, — по два; а пересечение всех трёх событий учитывается трижды (см. рис. 7).
Поэтому
Предложите учащимся убедиться в верности этого соотношения на примере нашей задачи. Действительно:
.
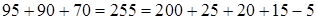Если разделить полученное равенство на общее количество элементарных событий эксперимента, то мы получим соотношение для вероятностей:
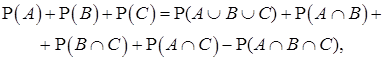
откуда
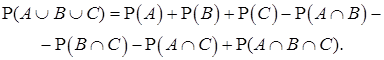
Замечание. Приведенное рассуждение о количестве элементарных исходов является справедливым только для случайных опытов, где количество элементарных исходов конечно. Поэтому его можно использовать только в качестве пояснения.
|
|
|
В хорошо подготовленном классе можно провести доказательство формулы в общем виде, используя формулу для двух событий.
Формула сложения вероятностей для трёх событий. Вероятность объединения трёх событий можно вычислить по формуле:
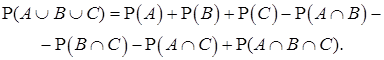
Пример 5. Контрольная работа по математике состоит из трёх задач. Работу выполняло 25 человек. Известно, что двое не решили ни одной задачи. 18 человек решили первую задачу, причём 12 из них решили и вторую задачу; 15 человек решили вторую задачу, причем 9 из них решили и третью задачу. Третью же задачу решили 14 человек, из них 10 справились с первой задачей. Найдите вероятность того, что случайно выбранный ученик класса решил все три задачи контрольной.
Желательный результат обсуждения. Пусть событие А заключается в том, что случайно выбранный ученик класса решил первую задачу, событие В — вторую, а событие С — третью. Из условия следует, что
, 
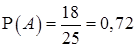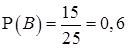и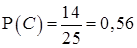 
.
Ясно, что хотя бы одну задачу решили 23 человека, поэтому
.
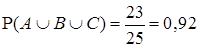Можно найти количество элементарных событий, благоприятствующих попарным пересечениям, а значит, найти их вероятност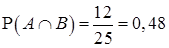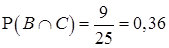и:
|
|
|
, 
и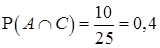 
.
Нам нужно найти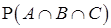 
. Из формулы сложения получаем:
Ответ: 0,28
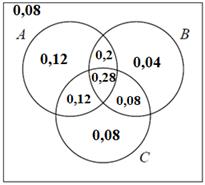Пример 6. Для предыдущей задачи (пример 5) нарисуйте диаграмму Эйлера и во всех восьми областях укажите вероятности соответствующих событий. При помощи диаграммы найдите вероятности события D «случайно выбранный ученик класса решил ровно две задачи» и события Е «случайно выбранный ученик класса решил ровно одну задачу».
Желательный результат обсуждения.
Диаграмма показана на рисунке 10. Вероятность дополнения сразу находится из условия. Зная вероятность пересечения всех трёх событий, легко найти вероятности прочих событий. В частности,
; 
.
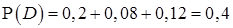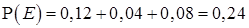Домашнее задание
1. В клубе путешественников состоит 40 человек. Ежегодно в канун нового года в клубе разыгрывается путёвка в Европу. В этом году разыгрывается путевка с автобусной экскурсией «Испания–Андорра–Франция». Среди членов клуба 18 человек уже были в Испании, треть из которых также посещали Андорру. Во Франции же побывала половина членов клуба, пятеро из которых также были и в Испании. В Андорре побывало 12 человек, причём тех, кто был в Андорре и не был ни в Испании, ни во Франции — нет. Во всех трёх странах побывали только два члена клуба. Какова вероятность того, что по выигранной путевке поедет турист, ни разу не бывавший ни в одной из трёх этих стран?
2. В олимпиаде по математике приняло участие 100 учащихся. Им было предложено решить одну задачу по алгебре, одну по геометрии и одну по теории вероятностей. Задачу по алгебре решили 63 человека, по геометрии — 46 человек, по теории вероятностей — 55 человек. Задачи по алгебре и геометрии решили 22 человека, по алгебре и теории вероятностей — 37 человек, по геометрии и теории вероятностей — 17 человек. Ни одной задачи не решили 3 человека. Найдите вероятность того, что случайно выбранный участник олимпиады:
а) решил все задачи;
б) решил только по одной задаче.
3*. Перед экзаменом по геометрии учитель выдал список из 100 экзаменационных задач. В каждом билете может оказаться любая одна из них. Антон, Артём и Андрей общими усилиями решили все 100 задач. Но каждый отдельно смог решить только 62 задачи. Назовём задачу трудной, если её решил только один, и легкой, если её решили все трое. На сколько отличается вероятность того, что случайно выбранная задача окажется лёгкой, от вероятности того, что она окажется трудной.
Дата добавления: 2021-04-15; просмотров: 4159; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!