Перечень рекомендуемых учебных изданий:
Практическая работа
Элементы математической логики и теория множеств
Элементы математической логики.
Основное неопределяемое понятие математической логики это высказывание. Под высказыванием понимают предложение, которое может принимать только два значения «истина» или «ложь». Обозначаются высказывания малыми латинскими буквами: a, b, ,…,х,…. или большими латинскими буквами A, B, C…
В математической логике не рассматривается смысл высказываний, определяется только их логическое значение – «истина» или «ложь». Известному немецкому математику и логику Эрнесту Шредеру пришло в голову предложить в качестве знака для обозначения ложного суждения цифру 0, что, конечно, привело к обозначению истины цифрой 1.
Исчисление высказываний – вступительный раздел математической логики, в котором рассматриваются логические операции над высказываниями.
Предикат – логическая функция от n переменных, которая принимает значения истинности или ложности.
Примеры.
- А=«Река Кола впадает в Кольский залив» – высказывание (истинное).
- В=«Число32 кратно 3» – высказывание (ложное).
- С=«Может быть, сегодня пойдет снег» – не высказывание.
- D=«5х – 9 = 7» – не высказывание (неопределенное высказывание или высказывательная форма).
С помощью простых высказываний можно составлять более сложные, соединяя простые высказывания союзами «и», «или», связками «не», «следует» и др. Операции над высказываниями можно описывать при помощи некоторого математического аппарата.
|
|
|
Основные логические операции над высказываниями.
Отрицанием высказывания х называется высказывание, которое истинно тогда и только тогда, когда высказывание х ложно. Отрицание обозначается 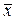 или -х (читается: «не х»).
или -х (читается: «не х»).
Логические операции можно задавать при помощи таблиц истинности, показывающих соответствие значений истинности высказываний. Для высказываний x и 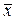 эта таблица имеет вид:
эта таблица имеет вид:
| х | 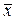
|
| 1 | 0 |
| 0 | 1 |
Конъюнкцией двух высказываний х и y называется высказывание, истинное тогда и только тогда, когда истинны оба высказывания х и y. Конъюнкция обозначается: х Ù y, или х & y (читается: «х и y»). Таблица истинности для х Ù y имеет вид:
| х | y | х Ù y |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
Дизъюнкцией двух высказываний х и y называется высказывание, ложное тогда и только тогда, когда оба высказывания х и y ложны. Дизъюнкция обозначается х Ú y (или x + y)(читается: «х или y»). Таблица истинности для х Ú y имеет вид:
| х | y | х Ú y |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Импликацией двух высказываний х и y называется высказывание, ложное тогда и только тогда, когда высказывание х истинно, а y – ложно. Импликация обозначается: х ® y (читается: «х влечет y» или «из х следует y»). Высказывание х называется посылкой импликации, а высказывание y – следствием. Таблица истинности для х ® y имеет вид:
|
|
|
| х | y | х ® y |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
Эквиваленцией (эквивалентностью) двух высказываний х и y называется высказывание, истинное тогда и только тогда, когда истинности высказываний х и y совпадают. Эквиваленция обозначается: х « y, или х ~ y (читается: «х эквивалентно y» или «х тогда и только тогда, когда y»). Таблица истинности для х « y имеет вид:
| х | y | х « y |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
Сложением по модулю два (альтернативной дизъюнкцией, логи́ческим сложе́нием, исключа́ющим «ИЛИ», строгой дизъюнкцией) двух высказываний х и y называется высказывание, истинное тогда и только тогда, когда оба высказывания х и y принимают разные значения. Дизъюнкция обозначается хÅy (читается: «или х, или y»). Таблица истинности для хÅy имеет вид:
|
|
|
| х | y | хÅy |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Стрелка Пирса – этоотрицание дизъюнкции. Стрелка Пирса обозначается X ↓ Y. Читается «ни X, ни Y». Введена в рассмотрение Чарльзом Пирсом (Сharles Peirce) в 1880—1881 г.г. Таблица истинности для стрелки Пирса имеет вид:
| х | y | х ↓ y |
| 1 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
Штрих Шеффера – это отрицание конъюнкции. Введена в рассмотрение Генри Шеффером в 1913 г. (в отдельных источниках именуется как Пунктир Чулкова). Штрих Шеффера обозначается x|y , задаётся следующей таблицей истинности:
| х | y | x|y |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
Алгебра Буля.
Множество высказываний с введенными для них логическими операциями дизъюнкции, конъюнкции и отрицания и основными законами этих действий называется алгеброй Буля. Алгебра Буля— исторически первый раздел математической логики, разработанный ирландским логиком и математиком Дж. Булем (George Boole (1815—1864) — английский математик и логик. Профессор математики Королевского колледжа Корка ). В середине XIX в. Буль применил алгебраические методы для решения логических задач и сформулировал на языке алгебры некоторые фундаментальные законы мышления
|
|
|
Законы алгебры Буля.
Коммутативные законы:
1. x Ù y º y Ù x;
2. x Ú y º y Ú x;
Ассоциативные законы:
1. x Ù (y Ù z) º (x Ù y) Ù z;
2. x Ú (y Ú z) º (x Ú y) Ú z;
Дистрибутивные законы:
| Законы логического сложения и умножения с 0 и 1:
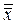 º x;
2. x Ú 0 º x;
3. x Ú 1 º 1;
4. º x;
2. x Ú 0 º x;
3. x Ú 1 º 1;
4. 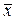 Ù x º 0;
5. Ù x º 0;
5. 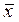 Ú x º 1; Ú x º 1;
|
Законы Де Моргана ( Augustus de Morgan (1806- 1871) — шотландский математик и логик; профессор математики в Университетском колледже Лондона):
-
 ;
; -
 .
.
Формулы алгебры логики
Формулами алгебры логикиназываются выражения, полученные из переменных x, y,… посредством применения логических операций: отрицания, конъюнкции, дизъюнкции, импликации и эквиваленции, а также сами переменные, принимающие значения истинности высказываний x, y,….
Если в формулу алгебры логики вместо переменных x, y,… подставить конкретные высказывания, то получится высказывание, имеющее логическое значение «1» или «0».
Пример.
Высказывание x: «Волга впадает в Каспийское море» – истинное (x = 1),
высказывание y: «Число 16 кратно 3» – ложное (y = 0),
тогда формула А = x Ú y будет иметь логическое значение «1»: А = 1 (см. таблицу истинности для х Ú y).
На основе таблиц истинности основных логических операций можно составлять таблицы истинности для различных формул алгебры логики.
Две формулы алгебры логики называются равносильнымиили эквивалентными, если они принимают одинаковые логические значения на любом наборе значений входящих в формулы переменных (элементарных высказываний). Равносильность формул будем обозначать знаком «º».
Равносильность логических формул можно установить при помощи их таблиц истинности.
Пример. С помощью таблиц истинности проверить, являются ли равносильными формулы  и
и 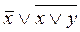 .
.
Решение. Составим таблицы истинности для каждой из формул А и В.
| x | y | 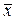
| 
| 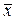 Ù Ù 
| 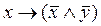
|
| 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 | 1 |
| x | y | 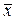
| x Ú y | 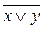
| 
|
| 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 | 1 |
Ответ: данные формулы являются равносильными.
Пример 2. Являются ли эквивалентными следующие высказывания: 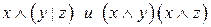
Решение.
Составим таблицы истинности для каждого высказывания.
| x | y | z | y|z | 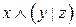
| 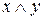
| 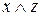
| 
|
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
Значения x и y в пятом и восьмом столбцах не совпадают.
Вывод: данные высказывания не являются эквивалентными.
Решение логических задач.
Исходя из разговорной практики, мы знаем, что, имея высказывания А и В, можно построить высказывания: не А (неверно, что А); А и В; А или В; если А, то В (из А следует В); А только и только тогда, когда В (А эквивалентно В, А тождественно В). Эти высказывания, в отличие от элементарных, естественно назвать сложными, поскольку они уже наделены структурой. Однако они так же, как и простые, могут принимать только два возможных значения: И либо Л.
Пример 3. Для составного высказывания «Пришла весна, и грачи прилетели» выделите простые, обозначив каждое из них буквой; запишите с помощью логических операций составное высказывание:
Решение: Обозначим через A-«пришла весна»; а через B- «грачи прилетели». Тогда высказывание С -«Пришла весна, и грачи прилетели» запишем так: С= А 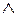 B. Ответ: С= А
B. Ответ: С= А 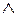 B.
B.
Пример 4. Определить значение истинности высказываний:
1) «7 является простым числом, или 19 является простым числом». Данное высказывание является сложным, поэтому обозначим А – «7 является простым числом», a В – «19 является простым числом». Имеем, что А=1, В=1. Составим формулу АÚВ и, используя таблицу истинности, найдем логическое значение формулы. Получим АÚВ= 1.
2) «2 + 3 = 6 и Архангельск расположен на Северной Двине». Данное высказывание является сложным, поэтому обозначим А – «2+ 3 = 6», а В-«Архангельск расположен на Северной Двине». Имеем, что А = 0, В = 1. Составим формулу АÙВ и, используя таблицу истинности, найдем логическое значение формулы. Получим АÙВ =0.
3) «Если 12 делится на 6, то 12 делится на 4». Данное высказывание является сложным, поэтому обозначим А- «12 делится на 6», а В – «12 делится на 4». Имеем, что А= 1,В=1. Составим формулу А®В и, используя таблицу истинности, найдем логическое значение формулы. Получим А®В= 1.
4) «11 делится на 3 тогда и только тогда, когда 20 делится на 5». Данное высказывание является сложным, поэтому обозначим А – «11 делится на 3», а В- «20 делится на 5». Имеем, что А=0, В = 1. Составим формулу А«В и, используя таблицу истинности, найдем логическое значение формулы. Получим А«В= 0.
Пример 5. Если будет холодно (А), то я надену теплое пальто (В), если рукав будет починен (С). Завтра будет холодно, а рукав не будет починен. Следует ли отсюда, что я не надену теплое пальто?
Решение. Посылки нашего рассуждения символически записываются следующим образом: А®(С®В), АÙ 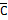 .Следует ли отсюда утверждение В ? Предположим, что высказывание В ложно, в то время как все посылки являются истинными высказываниями. Тогда В =0, а В = 1. Значит, первая посылка А®(С®В), действительно истинна, а вторая будет истинной, если А истинно, а С ложно. Таким образом, ситуация, когда все посылки истинны, а высказывание В ложно, вполне возможна. Это означает, что высказывание В не следует из данных посылок.
.Следует ли отсюда утверждение В ? Предположим, что высказывание В ложно, в то время как все посылки являются истинными высказываниями. Тогда В =0, а В = 1. Значит, первая посылка А®(С®В), действительно истинна, а вторая будет истинной, если А истинно, а С ложно. Таким образом, ситуация, когда все посылки истинны, а высказывание В ложно, вполне возможна. Это означает, что высказывание В не следует из данных посылок.
Множество. Способы задания множеств.
Одним из основных исходных понятий математики является понятие множества и его элементов. Множество состоит из элементов. Множества обозначаются большими латинскими буквами: A; B; C..., а их элементы - малыми буквами: a,b,c,…
Если a является элементом множества A или, что то же самое, a принадлежит множеству A, то применяют запись aÎA; в противном случае пишут aÏA.
Два множества A и B равны (A=B), если они состоят из одних и тех же элементов. Если множества A и B не равны, то применяется запись A ¹ B.
Множество, содержащее конечное число элементов, называется конечным, в противном случае множество называется бесконечным. Конечное множество, содержащее n элементов, называется n-множеством.
Множество, не содержащее элементов, называется пустым и обозначается Æ.
Предположим, что все множества, которые будут рассмотрены в этой главе, являются подмножествами некоторого множества U, называемого универсальным множеством.
а б

Рис. 1.1.
Если каждый элемент а множества В, аÎВ, является элементом множества А, аÎА, то В называется подмножеством множества А (рис. 1.1, а). Этот факт записывается с помощью знака включения Í следующим образом: ВÍА.
Свойства включения
1. АÍ А;
2. если АÍ В и ВÍС, то АÍС (рис. 1.1, б);
3. из двух включений ВÍА и АÍ В следует, что А=В.
Принято считать, что пустое множество является подмножеством любого множества.
Если ВÍ А и при этом В¹А, то этому соответствует запись ВÌ А и В называется собственным подмножеством А. В решении примера 1.1 все множества, кроме последнего, являются собственными подмножествами множества А.
Для описания множества A, состоящего из элементов a1,a2,...,an,... обычно применяется запись A={a1,a2,...,an,...}, причём порядок элементов в фигурных скобках не имеет значения; обычно он определяется соображениями наглядности.
Пример 1. В записи множества первых n натуральных чисел Nn={1,2,...,n} удобно располагать числа в возрастающем порядке, хотя при этом надо иметь в виду, что N3 ={1,2,3}={2,1,3}={3,2,1}.
Другой способ задания множества состоит в описании свойств, однозначно определяющих принадлежность элементов данному множеству. Такому способу задания множества соответствует запись: A ={a/a обладает свойством P(a)}.
Пример 2. Множество чётных чисел M может быть задано так: M={i / i - целое число, которое делится на 2 без остатка}.
В случае описания множества с помощью некоторого свойства необходимо следить за тем, чтобы каждый элемент был чётко определён. Так, например, недостаточно чётким является определение множества А как множества слов русского языка, если нет ссылки на один из толковых словарей.
Возможно также рекурсивное задание множества, при котором осуществляется последовательное описание элементов через предыдущие. Например, множество натуральных чисел рекурсивно можно задать так: N={i / если целое iÎN, то i+1ÎN, i ³ 1}.
Операции над множествами. Законы действий над множествами.
Объединением двух множеств А и В называется множество вида:
AÈB ={a / aÎ A или aÎ B}(рис. 1.2, а).
Пересечением двух множеств А и В называется множество вида:
AÇB={a / aÎ A и aÎ B} (рис. 1.2, б).
Если множества А и В не имеют общих элементов, то AÇB=Æ.
а б
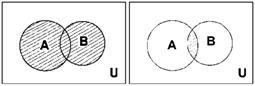
Рис. 1.2.
Свойства операций объединения и пересечения
1. AÈB = ВÈА, AÇB = ВÇА (коммутативность);
2. (AÈB)ÈС = AÈ(BÈС), (AÇB)ÇС = AÇ(BÇС) (ассоциативность).
3. Объединение и пересечение связаны законами дистрибутивности:
AÇ(BÈC)= (AÇB) È (AÇС); AÈ(BÇC)= (AÈB) Ç (AÈС).
По свойству 3 операции включения следует равенство правой и левой частей доказываемого равенства.
Для операции объединения множеств нейтральным является пустое множество Æ, а для операции пересечения множеств - универсальное множество U.
Разность множеств А и В определяется следующим образом:
A\B ={a / aÎA и aÏB} (рис. 1.3, а).
Разность не обладает свойством коммутативности; эта операция также не является и ассоциативной.
Пользуясь понятием универсального множества, можно определить дополнение  к множеству А, как разность вида:
к множеству А, как разность вида:  = U \ A (рис. 1.3, б).
= U \ A (рис. 1.3, б).
а) б)

Рис. 1.3.
Пример 3. Пусть в качестве универсального множества выступает множество целых чисел Z и пусть А - это множество всех чётных чисел. Тогда  - это множество всех нечётных чисел.
- это множество всех нечётных чисел.
Операции объединения, пересечения и дополнения множеств связаны между собой законами де Моргана:
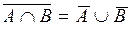 ,
, 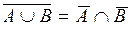 .
.
Пример 4.
1. Найти 

Решение: 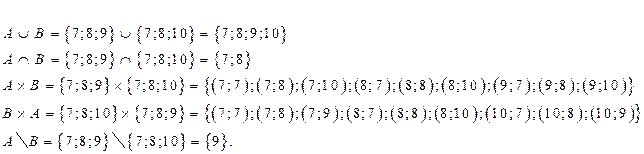
2. Доказать равенство и записать двойственное ему:



Решение:
Преобразуем левую часть:

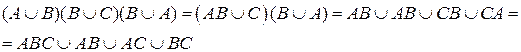
 Таким образом, левая часть равна правой части, т.е. равенство верно.
Таким образом, левая часть равна правой части, т.е. равенство верно.
Для того чтобы составить равенство, двойственное данному, пользуемся принципом двойственности. Заменим в данном равенстве знак 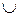 на
на 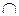 и наоборот. Чтобы не поменялся порядок действий, по другому поставим скобки. Получим двойственное равенство:
и наоборот. Чтобы не поменялся порядок действий, по другому поставим скобки. Получим двойственное равенство: 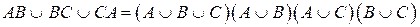
Релейно-контактные схемы
Релейно-контактной схемой (РКС) или переключательной схемой называется схематическое изображение устройства, состоящего из следующих элементов:
1) переключателей (контактов, реле, ламп и др.);
2) соединительных проводников;
3) входов-выходов (полюсов РКС).
Рассмотрим простейшую РКС, содержащую один переключатель Р. Если переключателю Р поставить в соответствие высказывание х: «Переключатель Р замкнут», то истинному значению х (х = 1) будет соответствовать замкнутое состояние переключателя, при котором РКС проводит ток, т.е. импульс, поступающий на вход, может быть снят на выходе. Значению х = 0 будет соответствовать разомкнутое состояние РКС (ток не проводится). Каждой РКС, состоящей из нескольких переключателей, можно поставить в соответствие высказывание, выраженное некоторой формулой А, таким образом, что истинному значению формулы (А = 1) будет соответствовать замкнутое состояние РКС, а значению А = 0 – разомкнутое состояние. Примеры таких соответствий приведены в таблице.
Простейшие РКС и соответствующие им формулы логики.
| РКС | Формула | Значения |
Переключатель х:

| Простейшее высказывание: х | х = 1, если переключатель замкнут; х = 0, если переключатель разомкнут |
Переключатель 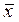
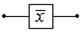
| Отрицание простейшего высказывания: 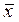
| 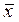 = 0, если переключатель замкнут; = 0, если переключатель замкнут;
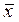 = 1, если переключатель разомкнут = 1, если переключатель разомкнут
|
Последовательное соединение:
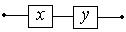 (схема замкнута, когда
оба переключателя замкнуты)
(схема замкнута, когда
оба переключателя замкнуты)
| Конъюнкция высказываний: x Ù y | 
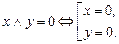
|
Параллельное соединение:
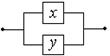 (схема разомкнута, когда
оба переключателя разомкнуты)
(схема разомкнута, когда
оба переключателя разомкнуты)
| Дизъюнкция высказываний: x Ú y | 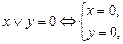

|
Схема, которая всегда разомкнута

| x Ù 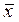
| x Ù 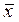 º 0 º 0
|
Схема, которая всегда замкнута
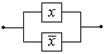
| x Ú 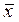
| x Ú 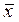 º 1 º 1
|
Из простейших РКС путем их последовательного и параллельного соединения могут быть построены более сложные переключательные схемы.
Доказано, что любая формула алгебры логики может быть преобразована к виду, содержащему только операции отрицания, конъюнкции и дизъюнкции. Это позволяет изображать логические формулы при помощи РКС, а РКС задавать формулами.
Например, согласно формулам основных равносильностей
x ® y º 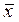 Ú y и x « y º (x ® y) Ù (y ® x),
Ú y и x « y º (x ® y) Ù (y ® x),
следовательно, логическим операциям импликации и эквиваленции соответствуют РКС, изображенные рис. 1.
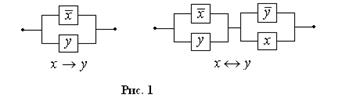
Используя равносильные преобразования логической формулы, соответствующей некоторой РКС, можно упростить РКС, т.е. привести ее к виду, содержащему меньшее число переключателей.
1.  Образец решения.
Образец решения.
Пример.
Упростить РКС, изображенную на рис. 2.
Решение. Запишем
соответствующую РКС формулу, используя таблицу простейших РКС и соответствующих им формул логики:
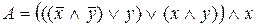 .
.
Упростим формулу, используя основные равносильности:
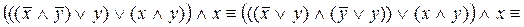


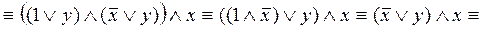

 .
.
Таким образом, 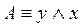 . Построим РКС, соответствующую упрощенной формуле (рис. 3).
. Построим РКС, соответствующую упрощенной формуле (рис. 3).
Содержание работы
Задание 3. Укажите, высказывание истинно или ложно: (Составить таблицы истинности)
3.1. 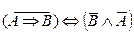
3.3. 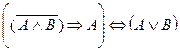
Задание 4. Являются ли эквивалентными следующие высказывания(таблицы истинности):
4.1. 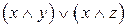 и
и 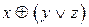
4.2.  и
и 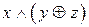
4.3.
Задание 5. Определить значение истинности высказываний:
5.1. «Число 6 делится на 2 и число 6 делится на 3».
5.2. «На уроке математики старшеклассники отвечали на вопросы учителя и писали самостоятельную работу».
5.3. «Число делится на 3 тогда и только тогда, когда сумма цифр числа делится на 3».
5.4. «Число 376 четное и трехзначное».
5.5. «Если сумма цифр числа делится на 3, то число делится на 3».
Задание 6. Для множеств А и В:
6.1.
1. Найти 
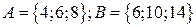
6.2.
1. Найти 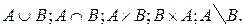
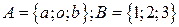
6.3.
1. Найти 
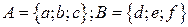
6.4.
1. Найти 
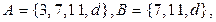
6.5.
1. Найти 
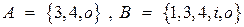
Вопросы для самоконтроля
- Что понимают в математической логике под высказыванием?
- Какие действия выполняются над высказываниями?
- Что называют алгеброй Буля?
- Перечислите законы алгебры Буля.
- Что понимают под множеством?
- Способы задания множеств.
- Какое множество называют пустым? Универсальным?
- Перечислите действия над множествами.
- Сформулируйте законы действий над множествами.
Перечень рекомендуемых учебных изданий:
Основная:
1. Филимонова Е.В. Математика: Учебное пособие для средних специальных учебных заведений. - Ростов н/Д: Феникс, 2009. – 416 с.
2. Омельченко В.П. , Кубатова Э.В. Математика: учебное пособие. - Ростов н/Д: Феникс, 2009. – 380 с.
3. Н.В. Богомолов. Практические занятия по математике. М. «Высшая школа».2009г.
4. Н.В. Богомолов. Математика. СПО. М.- «Дрофа». 2010 г.
5. Я.С. Бродский, Статистика. Вероятность. Комбинаторика., М. ОНИКС. Мир и образование, 2009, с. 541
Дополнительная:
1. Гмурман В.Е., Теория вероятности и математическая статистика. Учеб. Пособие для вузов. Изд. 7-е, стер. – М.: Высш. шк., 1999
2. Данко П.Е. и др. Высшая математика в упражнениях и задачах. Ч.1 7-е изд., - М.: ООО « Издательство «Мир и Образование», 2009
3. Фадеев М.А., Марков К.А., Основные методы вычислительной математики: учебное пособие. СПб.: Издательство «Лань», 2008 Афанасьева О.Н. и др., Сборник задач по математике для техникумов на базе средней школы. – М.: Наука, 1987.
4. Яковлев Г.Н. Алгебра и начала анализа, часть I, M. «Наука», 1978
5. Яковлев Г.Н. Алгебра и начала анализа, часть П, М «Наука», 1978. Шипачёв В.С. Начала высшей математики: Учебное пособие для вузов. – М.: Дрофа, 2004. – 384 с.: ил.
6. Валуцэ И.И., Дилигул Г.Д. Математика для техникумов на базе средней школы: Учебное пособие. – М.: Наука. Гл. ред. физ.-мат. лит., 1989.-576
7. Выгодский М.Я. Справочник по высшей математике. – М.: Высшая школа, 2000.
8. Щипачев В.С. Основы высшей математики. – М.: Высшая школа, 2000.
9. Д.Письменный. Конспект лекций по высшей математике. 1 часть. М. «Айрис Пресс». 2009г.
10. Д.Письменный. Конспект лекций по высшей математике. 2 часть. М. «Айрис Пресс». 2009г
Разработчик: Лебеденко И.А.
Дата добавления: 2021-04-15; просмотров: 55; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
