Каждая точка, до которой доходит волновое движение, служит центром вторичных волн; огибающая этих волн дает положение фронта волны в следующий момент.
Лекция 1
М-4 ВОЛНОВЫЕ ПРОЦЕССЫ. ВОЛНОВАЯ ОПТИКА
Механические и электромагнитные волны
Распространение колебаний в упругой среде. Продольные и поперечные волны. Основные характеристики волн: фазовая скорость, частота, волновое число, длина волны, фаза, фронт волны. Уравнения плоской и сферической волн. Волновое уравнение. Энергия и плотность энергии волны. Поток и плотность потока энергии волны. Вектор Умова.
Дифференциальные уравнения электромагнитной волны (волновые уравнения). Фазовая скорость электромагнитной волны. Уравнения плоской и сферической электромагнитных волн. Основные характеристики и свойства электромагнитных волн. Энергия электромагнитной волны. Вектор Пойнтинга. Шкала электромагнитных волн.
Рассмотрим новый вид движения, который называется волновым движением. Волна – возмущение (изменение) состояния среды или поля, распространяющееся с конечной скоростью и несущее с собой энергию. Важнейшее отличие волнового движения от любого другого упорядоченного движения состоит в том, что при малых возмущениях (отклонениях от состояния равновесия) распространение волн не связано с переносом вещества.
Рассмотрим упругую среду ‑ это может быть твердое тело, жидкость или газ. Между частицами среды существует взаимодействие. Если мы сместим из положения равновесия какую-либо частицу среды, то в результате этого взаимодействия сместятся из положения равновесия и соседние частицы.
|
|
|
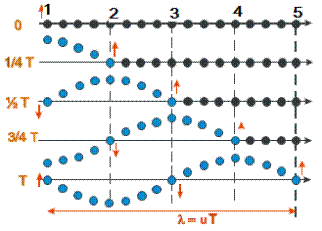
Рассмотрим это на примере цепочки одинаковых частиц упруго связанных друг с другом (рисунок 4.1.1). Пусть в какой-то момент времени 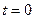 частица 1 начала смещаться из положения равновесия вверх. Она будет увлекать за собой соседние частицы. Через какое-то время, обозначим его
частица 1 начала смещаться из положения равновесия вверх. Она будет увлекать за собой соседние частицы. Через какое-то время, обозначим его 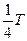 , частица 1 достигнет крайнего верхнего положения, а частица 2 начнет смещаться из положения равновесия вверх. Пройдет еще период времени
, частица 1 достигнет крайнего верхнего положения, а частица 2 начнет смещаться из положения равновесия вверх. Пройдет еще период времени 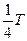 , частица 1 достигнет положения равновесия, и будет двигаться вниз; частица 2 достигнет крайнего верхнего положения; начнет движение вверх частица 3. Что произойдет в момент времени
, частица 1 достигнет положения равновесия, и будет двигаться вниз; частица 2 достигнет крайнего верхнего положения; начнет движение вверх частица 3. Что произойдет в момент времени  понятно из рисунка. В момент времени равный
понятно из рисунка. В момент времени равный 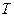 первая частица будет находиться в таком же состоянии движения, как и в начальный момент времени и начнет свое движение частица под номером 5. Процесс колебаний распространился на расстояние
первая частица будет находиться в таком же состоянии движения, как и в начальный момент времени и начнет свое движение частица под номером 5. Процесс колебаний распространился на расстояние 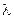 , или, другими словами, волна прошла путь
, или, другими словами, волна прошла путь  , где
, где 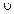 - скорость волны.
- скорость волны.
|
| Рисунок 4.1.1 ‑ Пример распространения волны в упругой среде, состоящей из одномерной цепочки частиц. |
В данном случае направление колебаний частиц перпендикулярны направлению распространения волны ‑ такие волны называются поперечными.
|
|
|
Можно провести подобные рассуждения и для случая смещения частиц вправо – влево.
Волна направление колебаний частиц среды в которой совпадает с направлением распространения волны называется продольной.
При распространении продольной волны в среде создаются чередующиеся сгущения и разряжения частиц (рисунок 4.1.2 – 4.1.3).

| 
|
| Рисунок 4.1.2 ‑ Схематическое изображение плоской продольной волны | Рисунок 4.1.3 ‑ Схематическое изображение сферической волны |
Фронт волны ‑ это поверхность, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли. Волновой фронт в каждый момент времени только один и все время перемещается.
Как построить волновой фронт? Это можно сделать с помощью принципа Гюйгенса.
Принцип Гюйгенса устанавливает способ построения фронта волны в момент времени t + Δt по известному положению фронта в момент времени t:
Каждая точка, до которой доходит волновое движение, служит центром вторичных волн; огибающая этих волн дает положение фронта волны в следующий момент.
Из рисунка 4.1.1, видно, что отклонение точки от положения равновесия зависит от времени и от положения точки. Функцию 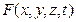 координат и времени называют фазой волны. Фаза волны - состояние волны в данной точке пространства в данный момент времени.
координат и времени называют фазой волны. Фаза волны - состояние волны в данной точке пространства в данный момент времени.
|
|
|
Рассматривая распространение волны в пространстве, следует ввести понятие волновой поверхности.
Волновой поверхностью называется геометрическое место точек, колеблющихся в одинаковой фазе.
Волновую поверхность можно провести через любую точку пространства, охваченного волновым процессом. Волновые поверхности остаются неподвижными, и их существует бесконечное множество. Волновые поверхности могут быть любой формы.
В простейших случаях они имеют форму или плоскости или сферы.
Соответственно волна в этих случаях называется или плоской или сферической.
В плоской волне волновые поверхности представляют собой множество параллельных друг другу плоскостей. Например, гребни волн на рисунке 4.1.2.
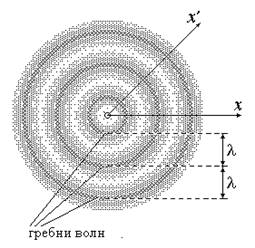
В сферической волне волновые поверхности представляют собой множество концентрических сфер (рисунок 4.1.3).
Линия, вдоль которой распространяется волна (в однородных средах это прямая линия) называется лучом.
Если источник колебаний очень мал (точечный источник), то волны от него радиально расходятся во все стороны. Вдоль луча x, как и вдоль луча x¢,происходит распространение колебаний. В рассматриваемом случае волновые поверхности (например, гребни волны) являются сферами.
|
|
|
Кроме плоских и сферических волн можно выделить также волны цилиндрические, у которых волновые поверхности – концентрические источнику цилиндры. Такие волны возбуждаются нитевидными или щелевыми источниками.
При дальнейшем рассмотрении мы будем предполагать, что во всех случаях выполняется принцип суперпозиции волн. Это вытекающее из опыта утверждение можно сформулировать следующим образом:
Если в среде распространяются одновременно несколько волн, то колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности.
Волны просто накладываются одна на другую, не возмущая друг друга.
Уравнение волны
Уравнением волны называется выражение, которое дает смещение колеблющейся частицы как функцию ее координа x , y , z и времени t : 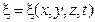 .
.
Волна называется гармонической, если изменение состояния среды или поля происходят по закону синуса или косинуса (по гармоническому закону).
Найдем вид функции x в случае плоской волны, полагая, что колебания являются гармоническими.
Волновые поверхности будут перпендикулярны к оси x и, поскольку все точки волновой поверхности колеблются одинаково, смещение x будет зависеть только от x и t: 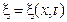 .
.
Пусть колебания точек, лежащих в плоскости x=0 , имеют вид: 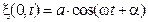 (рисунок 4.1.4).
(рисунок 4.1.4).
Найдем вид колебания точки в плоскости, соответствующей произвольному значению x.
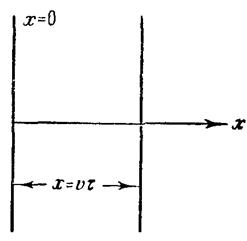
|
| Рисунок 4.1.4 ‑ К выводу уравнения плоской волны. |
Чтобы пройти путь от плоскости x = 0 до плоскости x = x, волне потребуется время: t = x/υ(υ – скорость распространения волны).
Колебания частиц, лежащих в плоскости x, будут отставать по времени на t от колебаний частиц в плоскости x=0 и будут иметь вид:
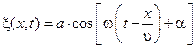 . (4.1.1)
. (4.1.1)
Это и есть уравнение плоской волны, которая распространяется в направлении оси x. Уравнению плоской волны можно придать симметричный относительно x и t вид.
Для этого введем величину, которая называется волновым числом 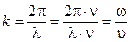
Тогда, уравнение плоской волны можно записать в виде:
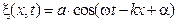 . (4.1.2)
. (4.1.2)
Проанализируем полученное уравнение плоской волны.
Положим начальную фазу равной нулю 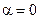 . Тогда из (4.1.1) получим
. Тогда из (4.1.1) получим
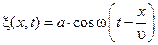 . (4.1.3)
. (4.1.3)
Зафиксируем какое либо значение фазы, стоящей в уравнении (7,3), положив:
 . (4.1.4)
. (4.1.4)
Выражение (4.1.3) дает связь между временем t и тем местом x, в котором зафиксированное значение фазы осуществляется в данный момент. Определив вытекающее из него значение 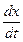 , мы найдем скорость, с которой перемещается данное значение фазы. Продифференцировав выражение (4.1.3), получим
, мы найдем скорость, с которой перемещается данное значение фазы. Продифференцировав выражение (4.1.3), получим
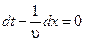 , откуда
, откуда  . (4.1.5)
. (4.1.5)
Таким образом, скорость распространения волны υ в уравнении (4.1.3) есть скорость перемещения фазы, в связи с чем ее называют фазовой скоростью.
Волна (4.1.3) периодична во времени и в пространстве. Период равен 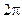 . Из периодичности во времени
. Из периодичности во времени  следует
следует 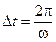 . Этот промежуток времени называют периодом колебаний:
. Этот промежуток времени называют периодом колебаний: 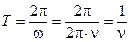 .
.
Из периодичности в пространстве 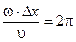 , следует
, следует  .
.
Расстояние между ближайшими точками среды, колеблющимися с разностью фаз 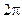 , называют длиной волны
, называют длиной волны  .
.
Таким образом, в отличие от гармонических колебаний, гармоническая волна характеризуется не только периодом колебаний, но и длиной волны.
Основываясь на формуле Эйлера 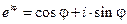 , уравнение плоской волны
, уравнение плоской волны 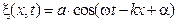 можно записать в экспоненциальной (комплексной) форме:
можно записать в экспоненциальной (комплексной) форме: 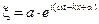 , где физический смысл имеет лишь действительная часть выражения. Такая форма представления волны существенно облегчает математические действия.
, где физический смысл имеет лишь действительная часть выражения. Такая форма представления волны существенно облегчает математические действия.
Найдем уравнение плоской волны, распространяющейся в произвольном направлении. Возьмем волновую поверхность (плоскость), отстоящую от начала координат на расстоянии l (рисунок 4.1.5). Колебания в этой плоскости будут отставать от колебаний в плоскости, проходящей через начало координат параллельно выбранной на время 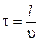 :
:
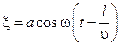 (4.1.6)
(4.1.6)
Выразим l через радиус-вектор 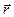 точек рассматриваемой поверхности. Для этого ввведемединичный вектор
точек рассматриваемой поверхности. Для этого ввведемединичный вектор 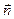 нормали к волновой поверхности. Легко видеть, что скалярное произведение
нормали к волновой поверхности. Легко видеть, что скалярное произведение 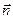 н радиус-вектор
н радиус-вектор 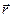 любой из точек поверхности имеет одно и тоже значение, равное l:
любой из точек поверхности имеет одно и тоже значение, равное l:
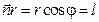 . (4.1.7)
. (4.1.7)

|
| Рисунок 4.1.5 – К выводу уравнения плоской волны, распространяющейся в произвольном направлении |
Подставим уравнение (4.1.7) для l в уравнение (4.1.6), внеся одновременно в скобки ω:
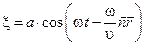 . (4.1.8)
. (4.1.8)
Отношение ω/υ равно волновому числу k. Вектор 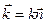 , равный по модулю волновому числу
, равный по модулю волновому числу 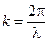 и имеющий направление нормали к волновой поверхности (направление луча), называется волновым вектором. Введя k в (4.1.8), получим:
и имеющий направление нормали к волновой поверхности (направление луча), называется волновым вектором. Введя k в (4.1.8), получим:
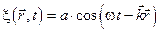 . (4.1.9)
. (4.1.9)
Функция (4.1.9) дает отклоненте от положения равновесия точки с радиус вектором 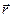 в момент времени t.
в момент времени t.
До сих пор мы говорили о волне, которая распространяется в среде, не поглощающей энергию волны. Если энергия волны поглощается средой, то опыт показывает, что в однородной среде интенсивность, а, следовательно, и амплитуда волны с удалением от источника колебаний уменьшается по экспоненциальному закону:
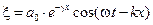 , (4.1.10)
, (4.1.10)
где  ‑ амплитуда волны в точках плоскости x=0. γ – коэффициент поглощения волны в среде (величина, обратная расстоянию, на котором амплитуда волны уменьшается в е раз).
‑ амплитуда волны в точках плоскости x=0. γ – коэффициент поглощения волны в среде (величина, обратная расстоянию, на котором амплитуда волны уменьшается в е раз).
Если рассматривать волны на расстояниях от источника колебаний значительно превышающих его размеры, то источник можно считать точечным. В изотропной и однородной среде волна, порождаемая точечным источником, будет сферической. Амплитуда колебаний в этом случае, даже если энергия волны не поглощается средой, не остается постоянной – она убывает с расстоянием от источника пропорционально 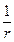 . Уравнение сферической волны, распространяющейся в среде без затухания:
. Уравнение сферической волны, распространяющейся в среде без затухания:
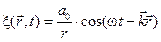 , (4.1.11)
, (4.1.11)
где  ‑ постоянная величина, численно равная амплитуде колебаний на расстоянии от источника, равном единице, размерность которой равна размерности колеблющейся величины, умноженной на размерность длины.
‑ постоянная величина, численно равная амплитуде колебаний на расстоянии от источника, равном единице, размерность которой равна размерности колеблющейся величины, умноженной на размерность длины.
Волновое уравнение
Аналогично основному уравнению динамики, которое описывает все возможные движения материальной точки, для волновых процессов, существуют уравнения, являющиеся обобщенным выражением волн, независимо от их конкретного вида. Это дифференциальные уравнения в частных производных, связывающие изменения функций, которые характеризуют волну, во времени и пространстве. Оказывается, что уравнение любой волны есть решение некоторого дифференциального уравнения, называемого волновым. Чтобы установить вид волнового уравнения, сопоставим вторые частные производные по координатам и времени от функции (4.1.9), описывающей плоскую волну. Продифференцировав (4.1.9) дважды по каждой из переменных, получим:
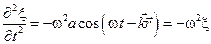 , (4.1.12)
, (4.1.12)
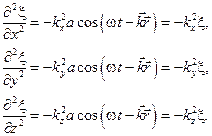 (4.1.13)
(4.1.13)
Сложим вместе уравнения (4.1.13):
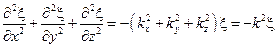 . (4.1.14)
. (4.1.14)
Теперь, сопоставляя уравнения (4.1.12) и (4.1.13), находим, что
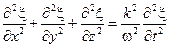 . (4.1.15)
. (4.1.15)
Наконец, учитывая, что 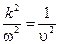 , получаем окончательно:
, получаем окончательно:
 . (4.1.16)
. (4.1.16)
Уравнение (4.1.16) и есть искомое волновое уравнение. Легко убедиться, что волновому уравнению удовлетворяет не только функция (4.1.9), но и любая функция вида
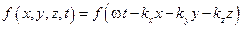 . (4.1.17)
. (4.1.17)
Всякая функция, удовлетворяющая уравнению вида (4.1.16), описывает некоторую волну, причем корень квадратный из величины, обратной коэффициенту при 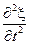 , дает фазовую скорость этой волны.
, дает фазовую скорость этой волны.
Уравнение (4.1.16) справедливо для однородных изотропных сред, затухание в которых пренебрежимо мало.
Образование электромагнитных волн.
Скорость распространения электромагнитных волн
Система уравнений Максвелла содержит все основные законы электрических и магнитных явлений в неподвижных средах. Важнейшим результатом теории Максвелла является ее вывод о существовании электромагнитных волн, распространяющихся со скоростью света. Теоретические исследования свойств электромагнитных волн привели Максвелла к электромагнитной теории света. Рассмотрим качественно, как из теории Максвелла следует существование электромагнитных волн.
X
а) б)
|
Рис. 4.1.6
Представим себе, что в некоторой точке О безграничной непроводящей среды определенным образом создано электрическое поле напряженности  (рис. 4.1.6 а). Если нет электрических зарядов, поддерживающих это поле, оно будет уменьшаться и, согласно второму уравнению Максвелла в системе уравнений, вызовет появление магнитного поля напряженности
(рис. 4.1.6 а). Если нет электрических зарядов, поддерживающих это поле, оно будет уменьшаться и, согласно второму уравнению Максвелла в системе уравнений, вызовет появление магнитного поля напряженности  . Величина и направление возникшего магнитного поля соответствуют току смещения плотности
. Величина и направление возникшего магнитного поля соответствуют току смещения плотности 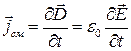 (для простоты считаем
(для простоты считаем 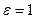 , то есть в качестве среды принимаем вакуум). Электрическое поле напряженности
, то есть в качестве среды принимаем вакуум). Электрическое поле напряженности  в точке О уменьшается, значит
в точке О уменьшается, значит 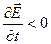 , и ток смещения в точке О направлен против вектора
, и ток смещения в точке О направлен против вектора  . Магнитное поле направлено по правилу правого винта по отношению к току, линии магнитного поля лежат в плоскости, перпендикулярной вектору
. Магнитное поле направлено по правилу правого винта по отношению к току, линии магнитного поля лежат в плоскости, перпендикулярной вектору  (и
(и 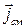 ) и направлены на рис.113 а по ходу часовой стрелки, если смотреть на них сверху. Если отсутствуют постоянные токи, поддерживающие магнитное поле
) и направлены на рис.113 а по ходу часовой стрелки, если смотреть на них сверху. Если отсутствуют постоянные токи, поддерживающие магнитное поле  , как будем предполагать, то оно будет исчезать. На основании первого уравнения Максвелла в переменное магнитное поле вызывает появление вихревого электрического поля (закон электромагнитной индукции). Согласно этой связи между полями в следующий момент времени появляется электрическое поле напряженности
, как будем предполагать, то оно будет исчезать. На основании первого уравнения Максвелла в переменное магнитное поле вызывает появление вихревого электрического поля (закон электромагнитной индукции). Согласно этой связи между полями в следующий момент времени появляется электрическое поле напряженности 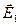 , которое по правилу Ленца направлено таким образом, чтобы вызванное им магнитное поле противодействовало изменению (в нашем случае уменьшению) магнитного потока поля напряженности
, которое по правилу Ленца направлено таким образом, чтобы вызванное им магнитное поле противодействовало изменению (в нашем случае уменьшению) магнитного потока поля напряженности  . Электрическое поле напряженности
. Электрическое поле напряженности 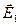 уничтожает первоначальное электрическое поле
уничтожает первоначальное электрическое поле  в точке О, но возбуждает в определенный момент времени поле в соседней точке 1. Ток смещения, порожденный уменьшением электрического поля напряженности
в точке О, но возбуждает в определенный момент времени поле в соседней точке 1. Ток смещения, порожденный уменьшением электрического поля напряженности 
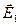 в точке 1, вызывает появление магнитного поля напряженности
в точке 1, вызывает появление магнитного поля напряженности 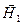 , направленного, как показано на рис.4.1.6 а, против магнитного поля напряженности
, направленного, как показано на рис.4.1.6 а, против магнитного поля напряженности  в этой точке. По этой причине
в этой точке. По этой причине 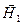 уменьшает ранее возникшее поле
уменьшает ранее возникшее поле  и появляется в более отдаленной от точки О точке пространства. В свою очередь, уменьшаясь, магнитное поле
и появляется в более отдаленной от точки О точке пространства. В свою очередь, уменьшаясь, магнитное поле 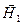 порождает вихревое электрическое поле
порождает вихревое электрическое поле 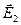 , которое будет ослаблять электрическое поле
, которое будет ослаблять электрическое поле 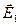 в точке 1, но появится в точке 2 и так далее. Таким образом, вместо первоначального электрического поля
в точке 1, но появится в точке 2 и так далее. Таким образом, вместо первоначального электрического поля  в точке О образовались взаимосвязанные электрические и магнитные поля, которые, порождая друг друга, распространяются в пространстве. Этот процесс распространения взаимно порождающих электрических и магнитных полей называется электромагнитной волной. Процесс образования электромагнитной волны подобен распространению сжатия и разряжения (или сдвига) при образовании упругой волны.
в точке О образовались взаимосвязанные электрические и магнитные поля, которые, порождая друг друга, распространяются в пространстве. Этот процесс распространения взаимно порождающих электрических и магнитных полей называется электромагнитной волной. Процесс образования электромагнитной волны подобен распространению сжатия и разряжения (или сдвига) при образовании упругой волны.
Качественные рассуждения, приводящие к представлению об электромагнитных волнах, подтверждаются результатами математического анализа системы уравнений Максвелла. Укажем на некоторые из них, касающиеся электромагнитных волн.
Из системы уравнений Максвелла получаются следующие дифференциальные уравнения второго порядка для векторов напряженностей электрического и магнитного полей:
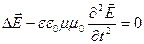 (4.1.18)
(4.1.18)
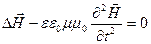
(напомним, что 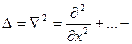 оператор Лапласа). (4.1.18) означает, что каждая проекция векторов
оператор Лапласа). (4.1.18) означает, что каждая проекция векторов  и
и  на оси, например, декартовой системы координат:
на оси, например, декартовой системы координат: 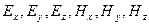 удовлетворяет аналогичному уравнению. (4.1.18) имеет вид волнового уравнения, встречавшегося при рассмотрении упругих волн. Таким образом, приходим к выводу, что переменное электромагнитное поле действительно распространяется в виде волны. Известно, что коэффициент при второй производной по времени в волновом уравнении является величиной, обратной квадрату фазовой скорости волны. Система волновых уравнений (4.1.18) указывает на то, что фазовая скорость электромагнитной волны
удовлетворяет аналогичному уравнению. (4.1.18) имеет вид волнового уравнения, встречавшегося при рассмотрении упругих волн. Таким образом, приходим к выводу, что переменное электромагнитное поле действительно распространяется в виде волны. Известно, что коэффициент при второй производной по времени в волновом уравнении является величиной, обратной квадрату фазовой скорости волны. Система волновых уравнений (4.1.18) указывает на то, что фазовая скорость электромагнитной волны  определяется следующей формулой:
определяется следующей формулой:
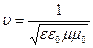 . (4.1.19)
. (4.1.19)
Для вакуума 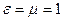 , и фазовая скорость электромагнитной волны в вакууме
, и фазовая скорость электромагнитной волны в вакууме
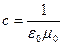 . (4.1.20)
. (4.1.20)
Следовательно, фазовую скорость электромагнитной волны в веществе можно записать в следующем виде:
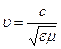 . (4.1.21)
. (4.1.21)
Вычисление скорости 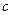 по формуле (4.1.20) показывает, что скорость электромагнитной волны в вакууме совпадает с известной скоростью распространения света в вакууме
по формуле (4.1.20) показывает, что скорость электромагнитной волны в вакууме совпадает с известной скоростью распространения света в вакууме 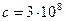 м/с. Основываясь на этом результате, Максвелл еще задолго до экспериментального подтверждения факта существования электромагнитных волн высказал предположение о том, что свет − это электромагнитные волны.
м/с. Основываясь на этом результате, Максвелл еще задолго до экспериментального подтверждения факта существования электромагнитных волн высказал предположение о том, что свет − это электромагнитные волны.
Плоские гармонические электромагнитные волны.
Шкала электромагнитных волн 
Наиболее простым электромагнитными волнами являются плоские электромагнитные волны, то есть волны, в которых поверхности одной фазы изменяющихся векторов 
 и
и 
 представляют собой плоскости, перпендикулярные направлению распространения волны, а сами указанные векторы зависят только от координаты, отсчитанной вдоль этого направления. Плоскую электромагнитную волну, распространяющуюся по оси
представляют собой плоскости, перпендикулярные направлению распространения волны, а сами указанные векторы зависят только от координаты, отсчитанной вдоль этого направления. Плоскую электромагнитную волну, распространяющуюся по оси 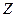 , по аналогии с плоской упругой волной, в общем виде можно подать следующим образом:
, по аналогии с плоской упругой волной, в общем виде можно подать следующим образом:
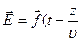 ),
), 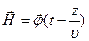 , (4.1.22)
, (4.1.22)
где 
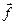 и
и 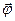 − определенные векторные функции аргумента
− определенные векторные функции аргумента 
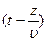 . В этом случае из уравнений Максвелла вытекает, что
. В этом случае из уравнений Максвелла вытекает, что 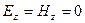 , то есть плоская электромагнитная волна поперечна. Поперечность свойственна всем электромагнитным волнам, а не только плоским: векторы
, то есть плоская электромагнитная волна поперечна. Поперечность свойственна всем электромагнитным волнам, а не только плоским: векторы  и
и  поля электромагнитной волны лежат в плоскости, перпендикулярной направлению распространения волны, то есть вектору ее скорости
поля электромагнитной волны лежат в плоскости, перпендикулярной направлению распространения волны, то есть вектору ее скорости 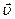 .
.
Из уравнений Максвелла можно получить для плоской электромагнитной волны (4.1.22) следующие формулы связи между проекциями напряженностей электрического и магнитного полей:
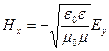 ,
, 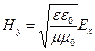 (4.1.23)
(4.1.23)
.
Из (4.1.23) следует два важных свойства электромагнитных волн. Во-первых, скалярное произведение векторов 
 и
и 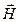 равно нулю:
равно нулю:
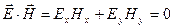 . (4.1.24)
. (4.1.24)
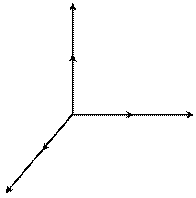
Это указывает на то, что векторы  и
и  поля электромагнитной волны взаимно перпендикулярны; это справедливо не только для плоской волны, но и в общем случае. Вместе с выводом о поперечности электромагнитной волны последнее утверждение означает, что векторы
поля электромагнитной волны взаимно перпендикулярны; это справедливо не только для плоской волны, но и в общем случае. Вместе с выводом о поперечности электромагнитной волны последнее утверждение означает, что векторы 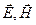 и
и 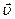 образуют правую тройку векторов: поворот правого винта от вектора
образуют правую тройку векторов: поворот правого винта от вектора  к вектору
к вектору  по минимальному углу (прямому в нашем случае) приводит к поступательному движению винта в направлении фазовой скорости волны
по минимальному углу (прямому в нашем случае) приводит к поступательному движению винта в направлении фазовой скорости волны 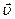 (рис.4.1.6 б).
(рис.4.1.6 б).
Второе свойство электромагнитных волн, вытекающее из равенств (4.1.23), состоит в связи между величинами напряженностей электрического и магнитного полей. Если возвести в квадрат оба равенства (4.1.23) а затем их сложить, получим: 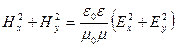 , или, учитывая поперечность волн (
, или, учитывая поперечность волн ( 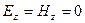 ):
):
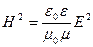 ,
, 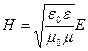 . (4.1.25)
. (4.1.25)
(4.1.25) устанавливает связь между величинами векторов  и
и  в электромагнитной волне. Пропорциональность величин
в электромагнитной волне. Пропорциональность величин 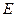 и
и 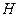 , отмеченная равенствами (4.1.25), показывает, что взаимно перпендикулярные векторы напряженностей электрического и магнитного полей в электромагнитной волне колеблются в одной фазе; они одновременно в данной точке пространства превращаются в нуль и одновременно достигают своих максимальных значений. Их модули в каждый момент времени в каждой выбранной точке электромагнитного поля связаны соотношением (4.1.25), которое справедливо для каждой бегущей электромагнитной волны независимо от формы ее волновых поверхностей.
, отмеченная равенствами (4.1.25), показывает, что взаимно перпендикулярные векторы напряженностей электрического и магнитного полей в электромагнитной волне колеблются в одной фазе; они одновременно в данной точке пространства превращаются в нуль и одновременно достигают своих максимальных значений. Их модули в каждый момент времени в каждой выбранной точке электромагнитного поля связаны соотношением (4.1.25), которое справедливо для каждой бегущей электромагнитной волны независимо от формы ее волновых поверхностей.
Если компоненты напряженностей электрического и магнитного полей в электромагнитной волне зависят от времени и координат точек пространства по законам косинуса или синуса, то имеем гармоническую электромагнитную волну. Гармоническая электромагнитная волна называется монохроматической волной. В каждой точке электромагнитного поля монохроматической волны проекции векторов  и
и  на оси координат совершают гармонические колебания одинаковой частоты, которая называется частотой волны.
на оси координат совершают гармонические колебания одинаковой частоты, которая называется частотой волны.
В поле плоской монохроматической волны, распространяющейся вдоль положительного направления оси 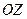 , проекции напряженностей меняются следующим образом:
, проекции напряженностей меняются следующим образом:
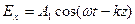 ,
, 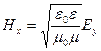 , (4.1.26)
, (4.1.26)
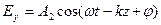 ,
, 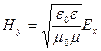 ,
,
где 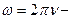 циклическая частота волны,
циклическая частота волны,  − волновое число,
− волновое число, 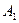 и
и 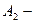 амплитуды проекций
амплитуды проекций 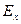 и
и 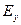 вектора напряженности электрического поля,
вектора напряженности электрического поля, 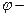 разность фаз колебаний этих проекций. При произвольном постоянном значении
разность фаз колебаний этих проекций. При произвольном постоянном значении 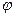 векторы
векторы  и
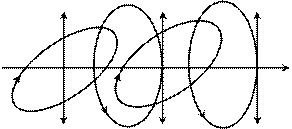
и  в каждой точке электромагнитной волны изменяются таким образом, что их концы описывают в плоскости, перпендикулярной направлению распространения волны, эллипсы. К такому выводу нетрудно прийти на основе сложения двух взаимно перпендикулярных колебаний одинаковой частоты.. В этом случае плоская монохроматическая волна называется эллиптически поляризованной.
в каждой точке электромагнитной волны изменяются таким образом, что их концы описывают в плоскости, перпендикулярной направлению распространения волны, эллипсы. К такому выводу нетрудно прийти на основе сложения двух взаимно перпендикулярных колебаний одинаковой частоты.. В этом случае плоская монохроматическая волна называется эллиптически поляризованной.
В случаях, когда 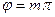 (
( 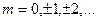 ), эллипсы превращаются в прямые, что означает колебания каждого из векторов
), эллипсы превращаются в прямые, что означает колебания каждого из векторов  и
и  в одном своем направлении. Такая волна называется линейно поляризованной (или плоско поляризованной).
в одном своем направлении. Такая волна называется линейно поляризованной (или плоско поляризованной).
 E
λ E
λ
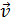 ΔS┴ Z
H
ΔS┴ Z
H
|
Рис. 4.1.7
На рис. 4.1.7 показаны векторы  и
и  поля плоской линейно поляризованной монохроматической волны в различных точках оси
поля плоской линейно поляризованной монохроматической волны в различных точках оси 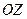 в определенный момент времени, причем ось
в определенный момент времени, причем ось 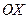 выбрана в направлении вектора
выбрана в направлении вектора  . Плоскость, походящая через электрический вектор
. Плоскость, походящая через электрический вектор  и линию распространения волны (луч), называется плоскостью колебаний, а перпендикулярная ей плоскость (в которой лежит вектор
и линию распространения волны (луч), называется плоскостью колебаний, а перпендикулярная ей плоскость (в которой лежит вектор  )
)  − плоскостью поляризации. В случае, изображенном на рис. 4.1.7, плоскостью колебаний является плоскость
− плоскостью поляризации. В случае, изображенном на рис. 4.1.7, плоскостью колебаний является плоскость 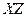 , плоскостью поляризации − плоскость
, плоскостью поляризации − плоскость  . В этом случае на основании (4.1.9) плоская монохроматическая волна записывается в следующем виде:
. В этом случае на основании (4.1.9) плоская монохроматическая волна записывается в следующем виде:
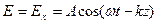 (4.1.27)
(4.1.27)

В зависимости от частоты  или длины волны в вакууме
или длины волны в вакууме 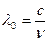 , а также способа излучения и регистрации электромагнитные волны делятся на несколько диапазонов: радиоволны, оптическое излучение (свет), рентгеновское излучение и гамма-излучение.
, а также способа излучения и регистрации электромагнитные волны делятся на несколько диапазонов: радиоволны, оптическое излучение (свет), рентгеновское излучение и гамма-излучение.
Радиоволнами называются электромагнитные волны, длина которых в вакууме 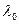 более 5·10-5 м; соответственно частота
более 5·10-5 м; соответственно частота 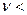 6·1012 Гц. Они излучаются движущимися заряженными частицами при определенных условиях.
6·1012 Гц. Они излучаются движущимися заряженными частицами при определенных условиях.
Оптическим излучением или светом называются электромагнитные волны, длины которых в вакууме лежат в диапазоне от 10 нм до 1 мм. Оно излучается атомами вещества при переходе валентного (оптического) электрона из одного энергетического состояния в другое. К оптическому излучению относятся инфракрасное, видимое и ультрафиолетовое излучение.
Инфракрасным называется электромагнитное излучение нагретых тел, длины волн которого в вакууме находятся в границах от 1 мм до 770 нм.
Видимым излучением, или видимым светом, называется электромагнитное излучение с длиной волны в вакууме от 770 нм до 380 нм, оно вызывает ощущение света в человеческом глазу.
Ультрафиолетовым называется электромагнитное излучение с длиной волны в вакууме от 380 нм до 10 нм.
Рентгеновским излучением, или рентгеновскими лучами, называется электромагнитное излучение, возникающее при взаимодействии заряженных частиц и фотонов с атомами вещества и характеризуется длинами волн в вакууме в условных границах от 10-100 нм до 0,01-1пм.
Гамма-излучение, или гамма-лучами, называется электромагнитное излучение с длинами волн в вакууме меньшими 0,1 нм, которое порождается возбужденными атомными ядрами при радиоактивных превращениях и ядерных реакциях, а также при некоторых взаимодействиях между элементарными частицами.
Первые опыты по обнаружению и изучению электромагнитных волн были проведены немецким ученым Генрихом Герцем в 1888 году. Он использовал открытый колебательный контур − так называемый вибратор с искровым промежутком . Для возбуждения электромагнитных колебаний в вибраторе к концам искрового промежутка В подводилось напряжение. Когда оно достигало определенной величины, в промежутке В возникала искра, которая соединяла обе части вибратора, в нем начинались свободные затухающие электромагнитные колебания, которые продолжались пока в промежутке В существовала искра. После этого вновь на концы промежутка В подавалось необходимое напряжение, и весь процесс повторялся. Таким образом вибратор Герца возбуждал в пространстве затухающие электромагнитные волны. Для приема электромагнитных волн Герц использовал такой же вибратор, но с меньшим искровым промежутком (он составлял доли мм). Под воздействием электромагнитных волн в приемном вибраторе возникают вынужденные колебания, и, если вибратор соединить с лампочкой накаливания, ее свечение будет свидетельствовать о приеме электромагнитных волн.
Энергия электромагнитной волны



Возможность обнаружения электромагнитных волн по свечению лампочки накаливания или другим способом указывает на то, что электромагнитные волны переносят энергию. Плотность энергии электромагнитного поля 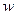 , то есть количество энергии в единице объема пространства, где существует электромагнитное поле, слагается из плотности энергии электрического поля
, то есть количество энергии в единице объема пространства, где существует электромагнитное поле, слагается из плотности энергии электрического поля  и плотности энергии магнитного поля
и плотности энергии магнитного поля 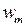 :
:
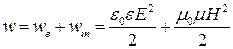 . (4.1.28)
. (4.1.28)
Из формулы (4.1.25) следует, что плотности энергии электрического и магнитного полей в электромагнитной волне одинаковы:
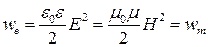 . (4.1.29)
. (4.1.29)
С помощью этого равенства плотность энергии электромагнитной волны можно записать в нескольких равнозначных видах:
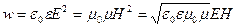 . (4.1.30)
. (4.1.30)
Количество энергии, переносимой электромагнитной волной через определенную поверхность в единицу времени, называется потоком энергии 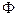 :
:
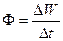 , (4.1.31)
, (4.1.31)
где 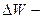 количество энергии (энергия) электромагнитной волны, переносимой за промежуток времени
количество энергии (энергия) электромагнитной волны, переносимой за промежуток времени 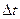 через определенную поверхность.
через определенную поверхность.
Пусть поток энергии 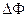 проходит через площадку
проходит через площадку  (рис.4.1.7) , перпендикулярную направлению распространения волны. Для характеристики переноса энергии определяется плотность потока энергии электромагнитной волны. Это вектор, численно равный количеству энергии, переносимой в единицу времени через единичную площадку, помещенную перпендикулярно направлению переноса энергии. Направлен вектор плотности потока энергии в направлении переноса энергии. Монохроматическая вона переносит энергию в направлении фазовой скорости
(рис.4.1.7) , перпендикулярную направлению распространения волны. Для характеристики переноса энергии определяется плотность потока энергии электромагнитной волны. Это вектор, численно равный количеству энергии, переносимой в единицу времени через единичную площадку, помещенную перпендикулярно направлению переноса энергии. Направлен вектор плотности потока энергии в направлении переноса энергии. Монохроматическая вона переносит энергию в направлении фазовой скорости 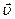 . Обозначая вектор плотности потока энергии
. Обозначая вектор плотности потока энергии 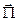 , на основе выше сформулированного определения получим:
, на основе выше сформулированного определения получим:
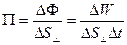 . (4.1.32)
. (4.1.32)
Количество энергии 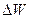 можно найти как энергию электромагнитного поля в объеме прямого цилиндра с основанием
можно найти как энергию электромагнитного поля в объеме прямого цилиндра с основанием  и высотой
и высотой 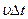 ,
, 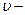 фазовая скорость волны. Если
фазовая скорость волны. Если  и
и 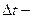 малые величины, то плотность энергии
малые величины, то плотность энергии 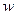 можно считать одинаковой во всех точках упомянутого объема. В таком случае
можно считать одинаковой во всех точках упомянутого объема. В таком случае
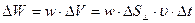 . (4.1.33)
. (4.1.33)
Подставляя (4.1.15) в (4.1.160, получим следующее выражение для величины вектора плотности потока энергии электромагнитной волны:
 . (4.1.34)
. (4.1.34)
Наконец, учитывая в (4.1.34) формулу (4.1.19) для скорости электромагнитной волны и (4.1.30) для плотности ее энергии, придем к следующему выражению:
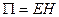 . (4.1.35)
. (4.1.35)
Векторы 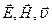 взаимно перпендикулярны и составляют правую тройку векторов; это означает, что направление вектора
взаимно перпендикулярны и составляют правую тройку векторов; это означает, что направление вектора 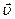 определятся по правилу правого винта (буравчика), если его поворачивать от вектора
определятся по правилу правого винта (буравчика), если его поворачивать от вектора  к вектору
к вектору  (по минимальному углу). Принимая это во внимание, приходим к векторной форме записи равенства (4.1.35):
(по минимальному углу). Принимая это во внимание, приходим к векторной форме записи равенства (4.1.35):
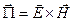 . (4.1.36)
. (4.1.36)
Вектор плотности потока энергии электромагнитной волны называется вектором Умова-Пойнинга.
Элементарный поток энергии 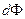 через площадку
через площадку 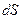 , согласно (4.1.32), можно записать в следующем виде:
, согласно (4.1.32), можно записать в следующем виде:
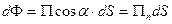 , (4.1.37)
, (4.1.37)
где 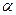 − угол между нормалью к площадке
− угол между нормалью к площадке 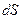 и направлением переноса энергии (направлением распространения волны),
и направлением переноса энергии (направлением распространения волны), 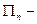 проекция вектора плотности потока энергии на нормаль к площадке
проекция вектора плотности потока энергии на нормаль к площадке 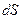 . Количество энергии (энергия), переносимая за единицу времени через определенную поверхность
. Количество энергии (энергия), переносимая за единицу времени через определенную поверхность 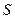 , то есть поток энергии
, то есть поток энергии 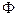 через поверхность
через поверхность 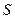 , получается после интегрирования выражения (4.1.37) по этой поверхности:
, получается после интегрирования выражения (4.1.37) по этой поверхности:
 . (4.1.38)
. (4.1.38)
Интенсивностью  монохроматической бегущей волны называется среднее значение вектора плотности потока энергии волны. Эту величину, используя выражение (4.1.34), можно записать в следующем виде:
монохроматической бегущей волны называется среднее значение вектора плотности потока энергии волны. Эту величину, используя выражение (4.1.34), можно записать в следующем виде:
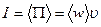 , (4.1.39)
, (4.1.39)
где 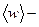 среднее за период изменения значение плотности энергии электромагнитного поля. Необходимо уточнить, какой промежуток времени является периодом изменения величины
среднее за период изменения значение плотности энергии электромагнитного поля. Необходимо уточнить, какой промежуток времени является периодом изменения величины 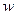 . Для плоской линейно поляризованной монохроматической волны (4.1.27) плотность энергии
. Для плоской линейно поляризованной монохроматической волны (4.1.27) плотность энергии 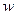 на основании (4.1.30)
на основании (4.1.30)
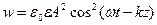 . (4.1.40)
. (4.1.40)
Как показывает выражение (4.1.40), значение 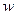 в каждой точке поля периодически колеблется с периодом в два раза меньшим величины
в каждой точке поля периодически колеблется с периодом в два раза меньшим величины  , являющейся периодом колебаний векторов
, являющейся периодом колебаний векторов  и
и  волны (так как в выражение (4.1.40) входит функция
волны (так как в выражение (4.1.40) входит функция 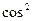 ). Следовательно, период изменения
). Следовательно, период изменения 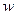 равен
равен 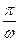 . Среднее за период изменения значение плотности энергии электромагнитного поля
. Среднее за период изменения значение плотности энергии электромагнитного поля
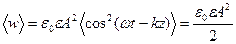 , (4.1.41)
, (4.1.41)
так как среднее значение функции 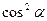 , если
, если 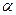 принимает все возможные значения от 0 до
принимает все возможные значения от 0 до 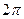 , равно
, равно 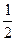 . Такой же результат получается для эллиптически поляризованной плоской монохроматической волны (4.1.26), если
. Такой же результат получается для эллиптически поляризованной плоской монохроматической волны (4.1.26), если 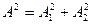 . Таким образом. В случае произвольной поляризации плоской монохроматической электромагнитной волны ее интенсивность
. Таким образом. В случае произвольной поляризации плоской монохроматической электромагнитной волны ее интенсивность  на основании равенства (4.1.39) с учетом (4.1.41) и (4.1.19) можно вычислить с помощью следующей формулы:
на основании равенства (4.1.39) с учетом (4.1.41) и (4.1.19) можно вычислить с помощью следующей формулы:
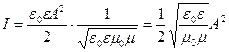 . (4.1.42)
. (4.1.42)
Выражение (4.1.42) показывает, что интенсивность плоской монохроматической бегущей электромагнитной волны прямо пропорциональна квадрату амплитуды  колебаний вектора напряженности электрического поля
колебаний вектора напряженности электрического поля  волны.
волны.
Дата добавления: 2021-04-15; просмотров: 44; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

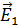
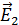
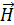 0
0 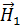 1 2 Z
1 2 Z