Тема 3. Сравнение положительных рациональных чисел

Тема 1. Свойства дробей

1.1. Как изменится правильная дробь, если ее числитель и знаменатель увеличить на одно и тоже натуральное число, меньшее знаменателя? Высказанное предположение докажите.

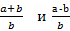1.2. Докажите, что если дробь сократима, то дроби тоже сократимы.

1.3. Верно ли, что при любом натуральном n числитель и знаменатель дроби 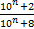делятся на 6? Ответ обоснуйте.

1.4. Известно, что дроби 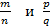равны и числитель первой дроби меньше числителя второй. Докажите, что в этом случае n <q.

Методические рекомендации

В данной теме представлены два типа задач. К первому относятся те, в которых исследуется вопрос о том, как изменяется данная дробь, если к ее числителю и знаменателю прибавить (вычесть) одно и то же число. Их решение основано на следующем свойстве отношения «больше» для чисел a и b: a>b тогда и только тогда, когда a-b>0.

Задачи второго типа связаны с понятием сократимой и несократимой дроби.

Для решения задач данной темы необходимо

знать: - основное свойство дроби; - определение несократимой дроби; - признаки делимости натуральных чисел на 2, 3, 5, 9 и др.; - теоремы о делимости суммы, разности и произведения; - правила выполнения действий с дробями.

уметь: - сокращать дроби; - выполнять арифметические действия с дробями.

Образец выполнения задания

Задача 1. Докажите, что правильная дробь уменьшится, если из ее числителя и знаменателя вычесть одно и то же натуральное число, меньшее числителя.

Решение: Запишем задачу, используя символы. Пусть - правильная дробь, а -такое натуральное число, что с< a. Если из числителя и знаменателя данной дроби вычесть с, то получим дробь 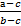. Покажем, что > .

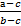Рассмотрим разность - 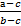. Если она окажется положительной, то данное утверждение будет доказано.

Используя правило вычитания дробей и свойства действий над натуральными числами, преобразуем эту разность:

- = = = = .

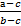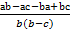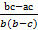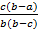В последней дроби разность 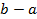положительна, т.к. по условию дробь - правильная, значит, b>a. Разность b-c тоже положительна, т.к. b>c (по условию c<a, a<b, но тогда по свойству транзитивности отношения «меньше» c<b или b>c). Значит, 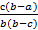>0, поэтому > 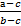, что и требовалось доказать.

Задача 2. Докажите, что числитель и знаменатель дроби делятся на 3.

Решение: Воспользуемся признаком делимости на 3. Сумма цифр в записи числителя равна 3 (сумма цифр числа 10ⁿравна 1, т.к. 10ⁿ=100...0). Соответственно сумма цифр знаменателя равна 6, но 6 кратно 3. Следовательно, числитель и знаменатель дроби делятся на 3.

Тема 2. Операции над положительными рациональными числами и их свойства

2.1. Докажите, что сложение положительных рациональных чисел коммутативно.

2.2. Сформулируйте определение отношения «меньше» для положительных рациональных чисел и докажите, что оно транзитивно.

2.3. Дайте определение разности положительных рациональных чисел. Сформулируйте условие ее существования в множестве положительных рациональных чисел и докажите его.

Методические рекомендации

В данной теме представлены задачи, в которых нужно доказать некоторые свойства действий над рациональными положительными числами или свойства отношений между ними. При этом в основу доказательств должны быть положены определения операций над положительными рациональными числами и уже известные свойства натуральных чисел.

Доказательство проводят следующим образом:

а) Представляют данные положительные рациональные числа дробями.

б) Следуя определениям действий над положительными рациональными числами, заменяют, например, сумму, произведение или частное рациональных чисел дробью, в числителе и знаменателе которой проводятся действия над натуральными числами.

в) Применяя к выражениям, состоящим из натуральных чисел, свойства, характерные для множества натуральных чисел, приводят эти выражения к требуемому виду.

г) Осуществляют переход от записи рационального числа в виде дроби к исходной записи.

Для решения задач данной темы необходимо

знать: - определения положительного рационального числа, сложения, вычитания и умножения рациональных чисел; - правила вычитания и деления рациональных чисел; - законы сложения и умножения натуральных и рациональных чисел.

уметь: - доказывать законы операций над положительными рациональными числами.

Образец выполнения задания

Задача. Докажите, что сложение положительных рациональных чисел ассоциативно.

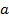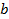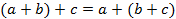Решение: Для того чтобы доказать, что для любых положительных рациональных чисел , и истинно равенство , представим числа 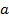, 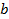и дробями с одинаковым знаменателем:

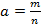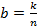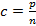, , , где , , и - натуральные числа.

Тогда . Воспользуемся правилом сложения дробей с одинаковым знаменателем:

Т.к. , , - натуральные числа, то на основании ассоциативного закона сложения натуральных чисел получим:

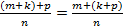По правилу сложения дробей имеем:

, что и требовалось доказать.

Тема 3. Сравнение положительных рациональных чисел

3.1. Расположите дроби в порядке возрастания: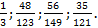

3.2. Каждую из дробей преобразуйте в несократимую и сравните их: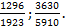

3.3. Запишите по два рациональных числа, заключенных между числами:

Методические рекомендации

В данной теме предлагаются задачи на сравнение положительных рациональных чисел. Их решение основано на применении практических приемов установления отношения «меньше» («больше») на множестве положительных рациональных чисел:

1. Если a = , b = , то a<b тогда и только тогда, когда m<p;

2. Если a = , b = , то a<b тогда и только тогда, когда mq<np, Для решения задач данной темы необходимо:

знать: - определение отношения «меньше» («больше») на множестве положительных рациональных чисел; - практические приемы установления отношения «меньше» («больше») на множестве положительных рациональных чисел;

уметь: - применять практические приемы сравнения положительных рациональных чисел на практике.

Образец выполнения задания

Задача. Какова несократимая запись дробе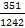й и ? Какая из данных дробей больше?

Решение:

Чтобы получить несократимую запись дроби, необходимо числитель и знаменатель разделить на их наибольший общий делитель. Для дроби 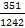найдем НОД при помощи алгоритма Евклида:

_1242ë351

1053 3

_ 351 ë 189

189 1

_ 189 ë162

162 1

_162 ë27

162 6

Итак, (351, 1242)= 27. Разделив 351 и 1242 на 27, получаем несократимую запись дроби .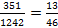

Аналогично находим НОД (143, 1012)=11. Следовательно,

Сравним дроб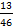и и 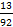. Их числители равны и потому та дробь больше, у которой знаменатель меньше, т.е. 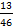> 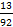, а значит > .

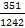Тема 4. Десятичные дроби

4.1. Какие из дробей можно записать в виде конечной десятичной дроби? 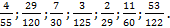Какие из них преобразуются в чистую, какие в смешанную периодическую бесконечную десятичную дробь? Ответ обоснуйте.

4.2. Следующие числа представьте в виде несократимых обыкновенных дробей: 0,05; 4,0016; 0,(27); 2,32(16); 6,038(72).

4.3. Сравните числа: 3,(4) и 3 ; 8,211216 и 8,(211).

Методические рекомендации

В данной теме представлены два типа задач. К первому относятся те, в которых положительное рациональное число представляется в виде десятичной конечной или бесконечной периодической дроби. Их решение основано на следующих положениях:

Любое положительное рациональное число можно представить в виде десятичной конечной или бесконечной периодической дроби. Если положительное рациональное число записано несократимой дробью и каноническое разложение знаменателя этой дроби содержит только 2 и 5, то его можно записать в виде конечной десятичной дроби, причем в ней будет столько десятичных знаков, сколько единиц будет содержать наибольшая степень числа 2 или 5 в каноническом разложении знаменателя q.

Если же в каноническом разложении знаменателя несократимой дроби , кроме 2 и 5 содержатся и другие простые множители, то данное рациональное число можно записать в виде бесконечной смешанной периодической десятичной дроби. И, наконец, если знаменатель q взаимно прост с числом 10, то данное рациональное число можно представить в виде чистой бесконечной периодической десятичной дроби.

Задачи второго типа связаны с записью бесконечной десятичной периодической дроби в виде обыкновенной. Их решение основано на правилах:

При обращении в обыкновенную дробь чистой периодической десятичной дроби получается дробь, числитель которой равен периоду, а знаменатель состоит из такого числа девяток, сколько цифр в периоде дроби.

При обращении в обыкновенную дробь смешанной периодической десятичной дроби, если целая часть этой дроби равна нулю, то получается дробь, числитель которой равен разности между числом, записанным цифрами, стоящими до начала второго периода, и числом, записанным цифрами, стоящими до начала первого периода; знаменатель состоит из такого числа девяток, сколько цифр в периоде, и такого числа нулей, сколько цифр стоит до начала первого периода.

Для решения задач данной темы необходимо

знать: - смысл записи числа в виде десятичной дроби; - правила записи положительных рациональных чисел в виде десятичных дробей; - правила записи бесконечных десятичных периодических дробей в виде обыкновенных.

уметь: - представлять любое положительное рациональное число в виде бесконечной десятичной периодической дроби; - выражать любую положительную бесконечную десятичную периодическую дробь в виде некоторого положительного рационального числа.

Образец выполнения задания

Задача 1. а) Представить в виде десятичной дроби числа: 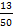; 2 ;

б) Записать дроби 0,(72); 0,012(27) в виде обыкновенных дробей.

Решение:

а) Каноническое разложение числа , значит, 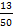может быть записана в виде конечной десятичной дроби с двумя десятичными знаками, т.к. наибольший показатель у 2 и 5 в разложении числа 50 равен 2. Эту дробь получим путем деления числителя на знаменатель. Имеем ;

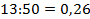Каноническое разложение числа 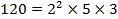, следовательно, число 2 может быть записано в виде смешанной периодической бесконечной десятичной дроби ; 2 = 2,141(6).

Несократимая дробь имеет знаменатель взаимно простой с числом 10, значит, дробь можно записать в виде чистой периодической бесконечной десятичной дроби .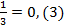

б) Решение: Чтобы чистую периодическую бесконечную десятичную дробь записать в виде обыкновенной, достаточно в числитель записать число, составленное из цифр периода, а в знаменатель число, составленное из 9, причем, их нужно взять столько, сколько цифр в периоде. Итак, 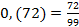. Сократим числитель и знаменатель на 9, получим .

Чтобы смешанную периодическую бесконечную десятичную дробь записать в виде обыкновенной, достаточно в числитель записать разность между числом, составленном из цифр, стоящих до второго периода, и числом, состоящим из цифр предпериода, а в знаменатель записать число, состоящее из 9, причем их написать столько, сколько цифр в периоде, и 0, а их написать столько, сколько цифр в предпериоде. Итак, 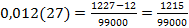или, сократив, получим .

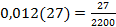Дата добавления: 2021-04-15; просмотров: 55; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 Следующая ⇒

Мы поможем в написании ваших работ!