Операция нахождения неопределенного интеграла от некоторой функции называется интегрированием этой функции.
ТЕМА «ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ С ОДНОЙ ПЕРЕМЕННОЙ»
ОПОРНЫЙ КОНСПЕКТ по теме:
«НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
МЕТОДЫ ИНТЕГРИРОВАНИЯ»
I. ПЕРВООБРАЗНАЯ И ИНТЕГРАЛ. ИЗ ИСТОРИИ.
Понятие интеграла и интегральное исчисление возникли из потребности вычислять площади любых фигур и поверхности и объемы произвольных тел. Предыстория интегрального исчисления восходит к глубокой древности. Идея интегрального исчисления была древними учеными предвосхищена гораздо в большей мере, чем идея дифференциального исчисления.
В продолжении ряда занятий мы познакомимся с основными понятиями, научимся использовать их. А сейчас просто короткая историческая справка:
АРХИМЕД (287-212 г.г. до н.э.) – его вклад в подготовку фундамента для создания интегрального исчисления огромен.
Для дальнейшего развития зачаточных интеграционных методов Архимеда необходимо было предварительно создать и развить новую алгебру с ее символикой, ввести понятия переменных, функции, и т.д.
Первые значительные попытки развития интеграционных методов Архимеда, увенчавшиеся успехом, были предприняты в XVII в., когда, с одной стороны, были достигнуты значительные успехи в области алгебры, а с другой – все более интенсивно развивались экономика, естествознание, техника, требовавшие более общих и мощных математических методов изучения и вычисления величин.
|
|
|
1609 г . – ИОГАНН КЕППЛЕР (1571-1630 г.г.) – опубликованы два закона движения планет, во втором из которых уже были предприняты попытки применения методов Архимеда.
1615 г . – ИОГАНН КЕППЛЕР – «Новая стереометрия винных бочек» - о вычислении площадей плоских фигур и поверхностей и объемов тел.
В то же время этими вопросами занимался Бонавентура Кавальери (ок. 1598-1647 г.г.), которого интересовали не практические задачи, а общая постановка и трактовка проблемы. Его труды сыграли большую роль в создании исчисления, но в них было много пробелов и недостатков.
Последователями Кавальери были ДЖОН ВАЛЛИС (1616-1703 г.г.) – «Арифметика бесконечных» (1655 г.), ПЬЕР ФЕРМА (1601-1665 г.г.) – вычисление интегралов для степени 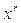 (1644 г.), БЛЕЗ ПАСКАЛЬ (1623-1662 г.г.) – «Трактат о синусе четверти круга» (1658 г.)
(1644 г.), БЛЕЗ ПАСКАЛЬ (1623-1662 г.г.) – «Трактат о синусе четверти круга» (1658 г.)
Признавая огромные заслуги Б.Паскаля, следует, однако, отметить, что он не пользовался новой символической алгеброй и не производил алгебраических выкладок, он все выражал словами, что лишило его возможности создать новый общий алгоритм, который открыли И.Ньютон и Г.Лейбниц.
1686 г . – ГОТФРИД ВИЛЬГЕЛЬМ фон ЛЕЙБНИЦ (1646-1716 г.г.) – «О глубокой геометрии и анализе неделимых, а также бесконечных» - первая печатная работа по интегральному исчислению, в которой установлена связь между интегральным и дифференциальным исчислениями.
|
|
|
Независимо от Г.Лейбница и еще до него эти результаты были получены ИСААКОМ НЬЮТОНОМ (1643-1727 г.г.), который нашел их, идя совсем по другому пути.
1671 г . – ИСААК НЬЮТОН – «Метод флюксий» (флюксия - производная) – хотя к основным понятиям и алгоритму исчисления И.Ньютон пришел в середине 60-х г.г. XVII в., когда двадцатилетний Г.Лейбниц был студентом юридического факультета и математикой не занимался.
В XVIII в. наибольший вклад в развитие и популяризацию дифференциального и интегрального исчислений внес ЛЕОНАРД ЭЙЛЕР (1707-1783 г.г.), написавший 3-хтомник по математическому анализу (1748, 1755, 1768-1769 г.г.). На трудах Л.Эйлера воспитывалось целое поколение математиков второй половины XVIII в. и первой четверти XIX в.
Далее развитием интегрального и дифференциального исчислений занимались ЖОЗЕФ ЛУИ ЛАГРАНЖ (1736-1813 г.г.), ОГЮСТЕН КОШИ (1789-1857 г.г.), БЕРНХАРД РИМАН (1826-1866 г.г.). Большой вклад внесли русские математики МИХАИЛ ВАСИЛЬЕВИЧ ОСТРОГРАДСКИЙ (1801-1862 г.г.) И ПАФНУТИЙ ЛЬВОВИЧ ЧЕБЫШЕВ (1821-1894 г.г.). Работы П.Чебышева в области анализа и его приложений были успешно продолжены его учениками А.М. ЛЯПУНОВЫМ (1857-1918 г.г.), В.А.СТЕКЛОВЫМ(1864-1923 г.г.), С.Н.БЕРНШТЕЙНОМ (1880-1968 г.г.).
|
|
|
Глубокие исследования, предпринятые в области анализа в конце XIX в. и начале XX в., связаны с развитием теории функций, теории множеств и других отраслей современной математики.
II. ПЕРВООБРАЗНАЯ ФУНКЦИЯ. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
Основной задачей дифференциального исчисления является нахождение производной или дифференциала данной функции.
Интегральное исчисление решает обратную задачу – нахождение самой функции по ее производной или дифференциалу.
Определение 1: Функция F ( x ) называется первообразной функцией для функции f ( x ) на промежутке I , если в каждой точке x этого промежутка F  ( x )= f ( x ).
( x )= f ( x ).
Пример: F(x) = 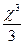 ; т.к .F
; т.к .F  (x) = f(x) = x
(x) = f(x) = x 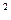 ;
;
F(x) = -сtg x т.к. F  (x) = f(x) =
(x) = f(x) = 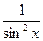
Но F  (x) =
(x) =  +5; F
+5; F  (x) =
(x) =  -2; F
-2; F 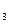 (x) =
(x) =  +25,094 таковы,
+25,094 таковы,
что F 
 (x)=F
(x)=F 
 (x)=F
(x)=F 
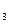 (x)= x
(x)= x 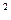 ,
,
т.е. для заданной функции существует множество первообразных, отличающихся друг от друга постоянным слагаемым.
Основное свойство первообразных:
Если F ( x ) – одна из первообразных функции f ( x ) на промежутке I , то все множество ее первообразных может быть записано в виде F ( x )+ C , где С – любое действительное число.
|
|
|
Определение 2: Совокупность всех первообразных для функции f(x) на промежутке I называется неопределенным интегралом от функции f(x) и обозначается 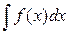 , где
, где  -знак интеграла; f(x) – подынтегральная функция; f(x)dx – подынтегральное выражение.
-знак интеграла; f(x) – подынтегральная функция; f(x)dx – подынтегральное выражение.
Таким образом, из определения неопределенного интеграла и основного свойства первообразной следует выполнение равенства
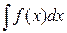 = F(x)+C (*), = F(x)+C (*),
|
где F(x) – некоторая первообразная для f(x), С – произвольная постоянная.
Примеры:  =
=  +С, т.к.
+С, т.к.  - первообразная для
- первообразная для 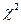
.

 - ctgx +C, т.к. -ctgx – первообразная
- ctgx +C, т.к. -ctgx – первообразная
для 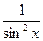 .
.
Операция нахождения неопределенного интеграла от некоторой функции называется интегрированием этой функции.
III. СВОЙСТВА НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА.
1. Производная от неопределенного интеграла равна подынтегральной функции: 
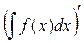 =f(x).
=f(x).
2. Дифференциал неопределенного интеграла равен подынтегральному
выражению: d 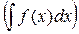 =f(x)dx.
=f(x)dx.
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого:
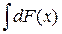 = F(x) + C.
= F(x) + C.
4. Постоянный множитель можно выносить за знак интеграла: 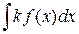 =
=  .
.
5. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций: 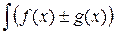 dx =
dx = 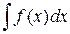
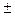
 .
.
6. .Пусть F(x) – некоторая первообразная для функции f(x). Тогда 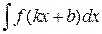 =
= 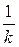 F
F 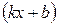 +C, где k и b – некоторые числа, k
+C, где k и b – некоторые числа, k  0.
0.
IV. ТАБЛИЦА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
1. 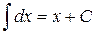
2. 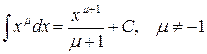
3. 
4. 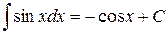
5. 
6. 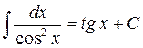
7. 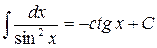
8. 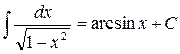
9. 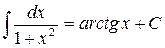
10. 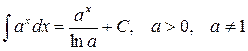
11. 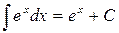
Дата добавления: 2021-04-15; просмотров: 67; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
