Задачи для решения на закрепление нового материала. Разобрать и кратко записать решение.

Занятие по теме «Элементы комбинаторики»

Цели:

- формирование основных понятий комбинаторики: размещения из mэлементов по n, сочетания из m элементов по n, перестановки из nэлементов;

- формирование умений и навыков вычисления значений комбинаторных выражений по формулам, решения простейших комбинаторных задач.

После изучения темы должны:

знать:

-определения трех важнейших понятий комбинаторики:

- размещения из n элементов по m;

- сочетания из n элементов по m;

- перестановки из n элементов, а также, формулы вычисления их количества.

уметь:

- отличать задачи на «перестановки», «сочетания», «размещения» друг от друга;

- применять основные комбинаторные формулы при решении простейших комбинаторных задач.

План занятия.

Изложение нового материала.

Введение общих понятий.

Комбинаторикой называют область математики, которая изучает вопросы о числе различных комбинаций (удовлетворяющих тем или иным условиям), которые можно составить из данных элементов.

Комбинаторика – раздел математики, в котором исследуются и решаются задачи выбора элементов из исходного множества и расположения их в некоторой комбинации, составляемой по заданным правилам.

Группы, составленные из каких-либо элементов, называются соединениями.

Различают три вида соединений: размещения, перестановки и сочетания.

Задачи, в которых производится подсчет возможных различных соединений, составленных из конечного числа элементов по некоторому правилу, называются комбинаторными, а раздел математики, занимающийся их решением, - комбинаторикой. Рассмотрим три основных вида соединений и формулы вычисления их количества. Для этого сначала рассмотрим 2 задачи, которые помогут нам сосредоточиться на сути новых понятий.

Задача 1. В некотором учреждении имеются две различные вакантные должности, на каждую из которых претендуют три сотрудника: A, B, C. Сколькими способами из этих трех кандидатов можно выбрать два лица на эти должности?

Задача 2. Для участия в соревнованиях требуется выбрать двоих спортсменов из трех кандидатов: A, B, C. Сколькими способами можно осуществить этот выбор?

Рассмотрев эти задачи, можно:

1) установить различие между этими двумя внешне схожими задачами;

2) предположить, в какой задаче результат будет больше, и почему.

Решаем эти задачи методом перебора всевозможных вариантов.

Решение задачи 1. AB, BA, BC, CB, AC, CA (всего шесть способов).

Решение задачи 2. AB, BC, AC (всего три способа).

Обратите внимание на то, что эти задачи оказались похожими только внешне, из-за того, что в обеих присутствуют два числа: m=3 – общее количество элементов и n=2 – количество выбранных элементов. Но в первой задаче составляются упорядоченные соединения, тогда как во второй задаче порядок следования элементов в соединении не имеет значения.

А если вместо чисел 3 и 2 будут например числа 8 и 3. Подойдет ли этот метод для решения этих задач? Поэтому существуют комбинаторные формулы для этих соединений.

Лекция «Основные комбинаторные понятия и формулы».

И начнём мы изучение комбинаторики с такого понятия, как факториал.

Что такое факториал?

Это слово происходит от латинского «factorialis», что означает «умножающий». И неспроста: в основе вычисления любого факториала стоит обыкновенное умножение.)) Итак, что же такое факториал.

Возьмём какое-нибудь натуральное число n. Совершенно произвольное: хотим 2, хотим 10, - какое угодно, лишь бы натуральное.)

Определение Факториал натурального числа n – это произведение всех натуральных чисел от 1 до n включительно. Обозначается вот так: n! То есть,

Чтобы не расписывать каждый раз это длинное произведение, просто придумали краткое обозначение. :) Читается немного непривычно: «эн факториал» (а не наоборот «факториал эн», как может показаться).

Например, ;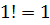

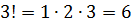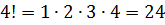
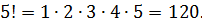
Улавливаете идею?)) Отлично! Тогда считаем примеры:

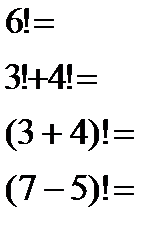
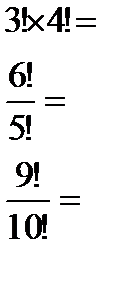
Ответы (в беспорядке): 30; 0,1; 144; 6; 720; 2; 5040, запишите правильно.

Всё получилось? Прекрасно! Считать факториалы и решать простейшие примеры с ними уже умеем.

Свойства факториала

Рассмотрим не очень понятное с точки зрения определения факториала выражение 0! Так уж в математике договорились, что

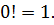
Да-да! Такое вот интересное равенство. Что от единицы, что от нуля факториал один и тот же – единичка.)) Пока примем это равенство за догму, а вот почему это именно так, будет ясно чуть позже, на примерах.))

Следующие два очень похожих свойства:

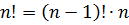
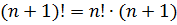
Эти две формулы позволяют, во-первых, легко считать факториал текущего натурального числа через факториал предыдущего числа. Или следующего через текущий.) Такие формулы в математике называются рекуррентными.

Во-вторых, с помощью этих формул можно упрощать и считать некоторые хитрые выражения с факториалами. Типа таких.

Вычислить:

Как действовать будем? Последовательно перемножать все натуральные числа от 1 до 1999 и от 1 до 2000? Это одуреешь! А вот по свойствам пример решается буквально в одну строчку:

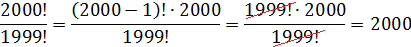
Или такое задание. Упростить: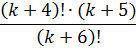

Снова работаем прямо по свойствам:

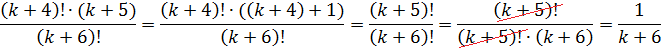
Элементы комбинаторики.

Размещения.

Определение. Размещениями из m элементов по n элементов ( n ≤ m ) называются такие соединения, каждое из которых содержит n элементов, взятых из m данных разных элементов, и которые отличаются одно от другого либо самими элементами, либо порядком их расположения.

Число размещений из m элементов по n обозначают 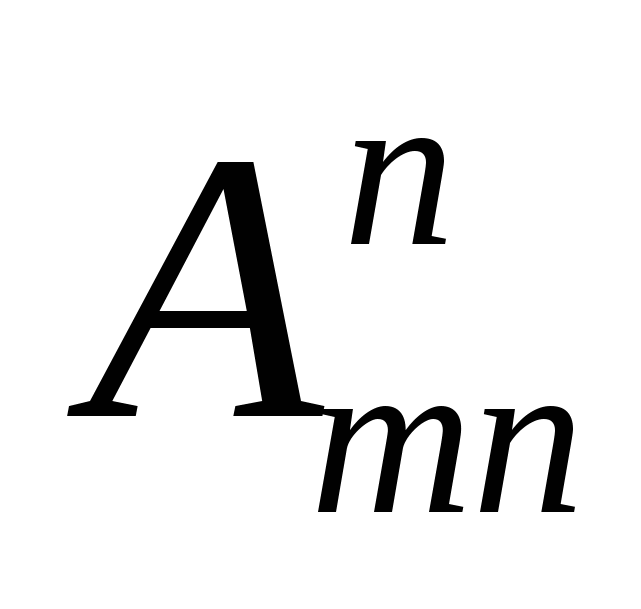(от французского «arrangement» - «размещение») и вычисляют по формуле:

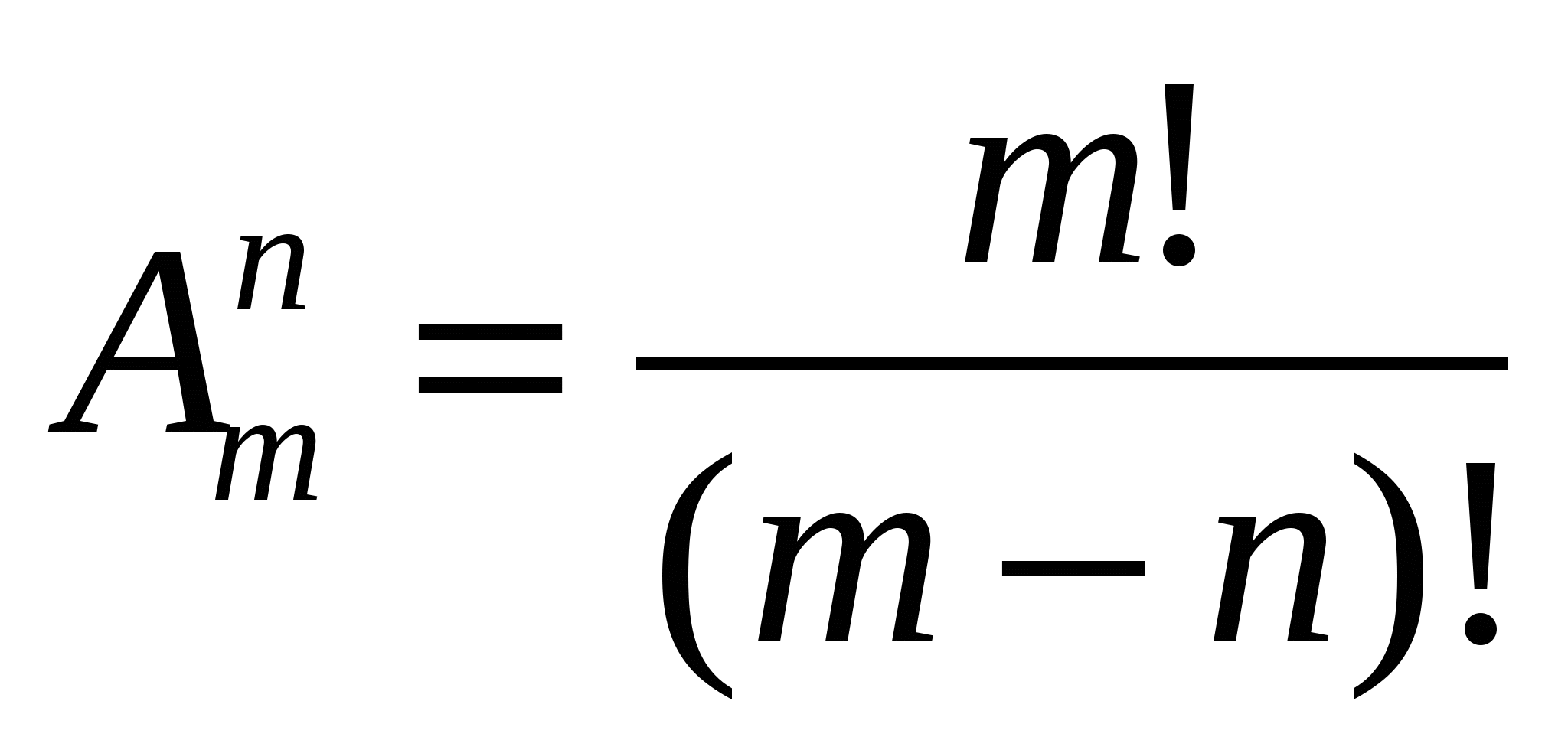
Пример 1. Решим задачу 1 с помощью этой формулы:

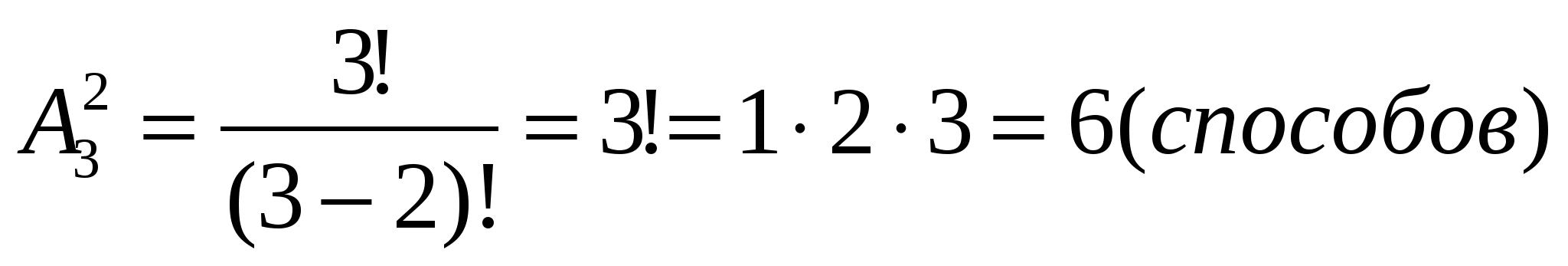
А теперь решим ту же задачу для случая m=8, n=3:

Перестановки.

Определение. Перестановкой из n элементов называют размещение из n элементов по n.

Число перестановок из n элементов обозначается 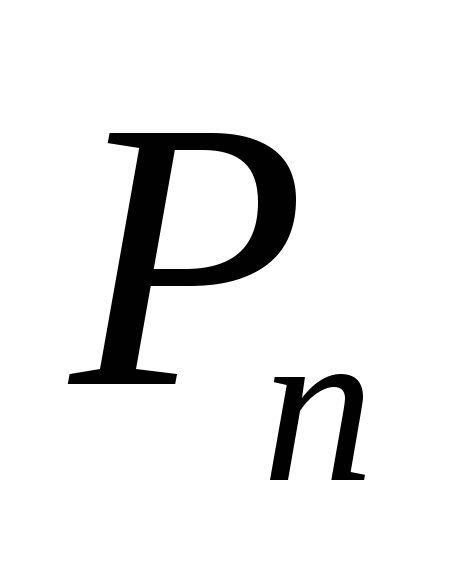и вычисляется по формуле:

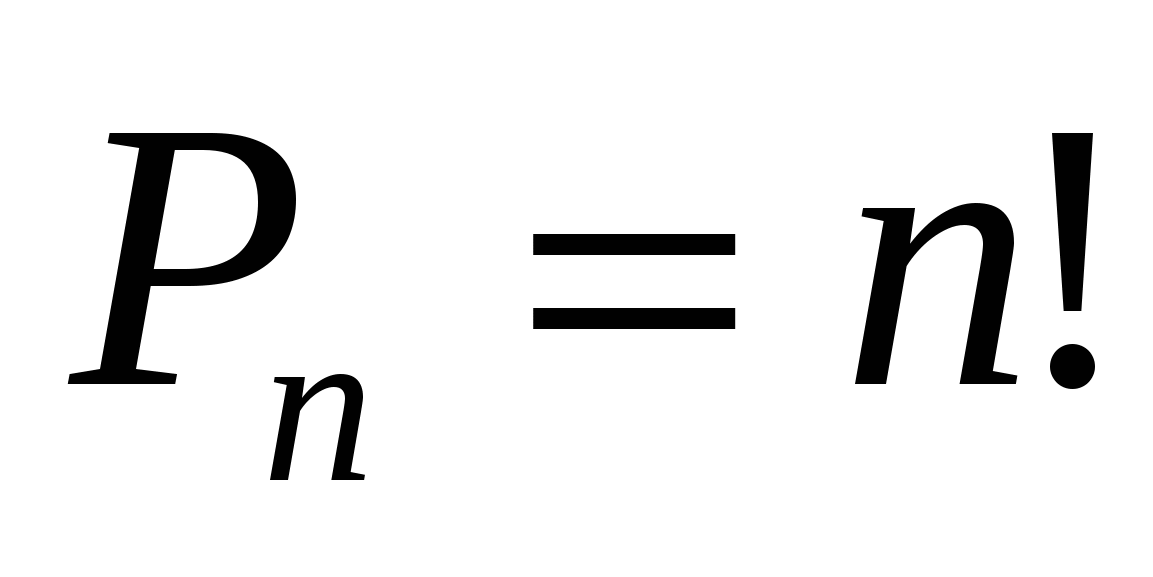
Задача. Сколькими способами можно расположить в столбик три детали конструктора, различающиеся по цвету?

Ответ:6.

Сочетания.

Определение.

Сочетаниями из m элементов по n элементов ( n ≤ m ) называются такие соединения, каждое из которых содержит n элементов, взятых из m данных элементов, и которые отличаются друг от друга по крайней мере одним элементом.

Число сочетаний из n элементов по m обозначают 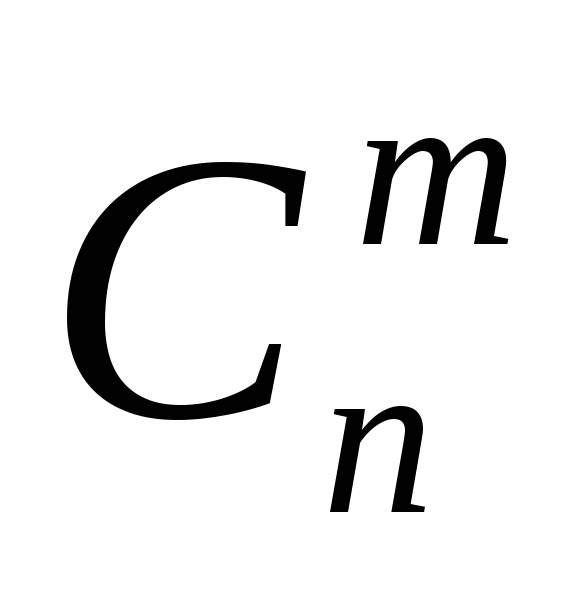(от французского «combination» - «сочетание») и вычисляют по формуле:

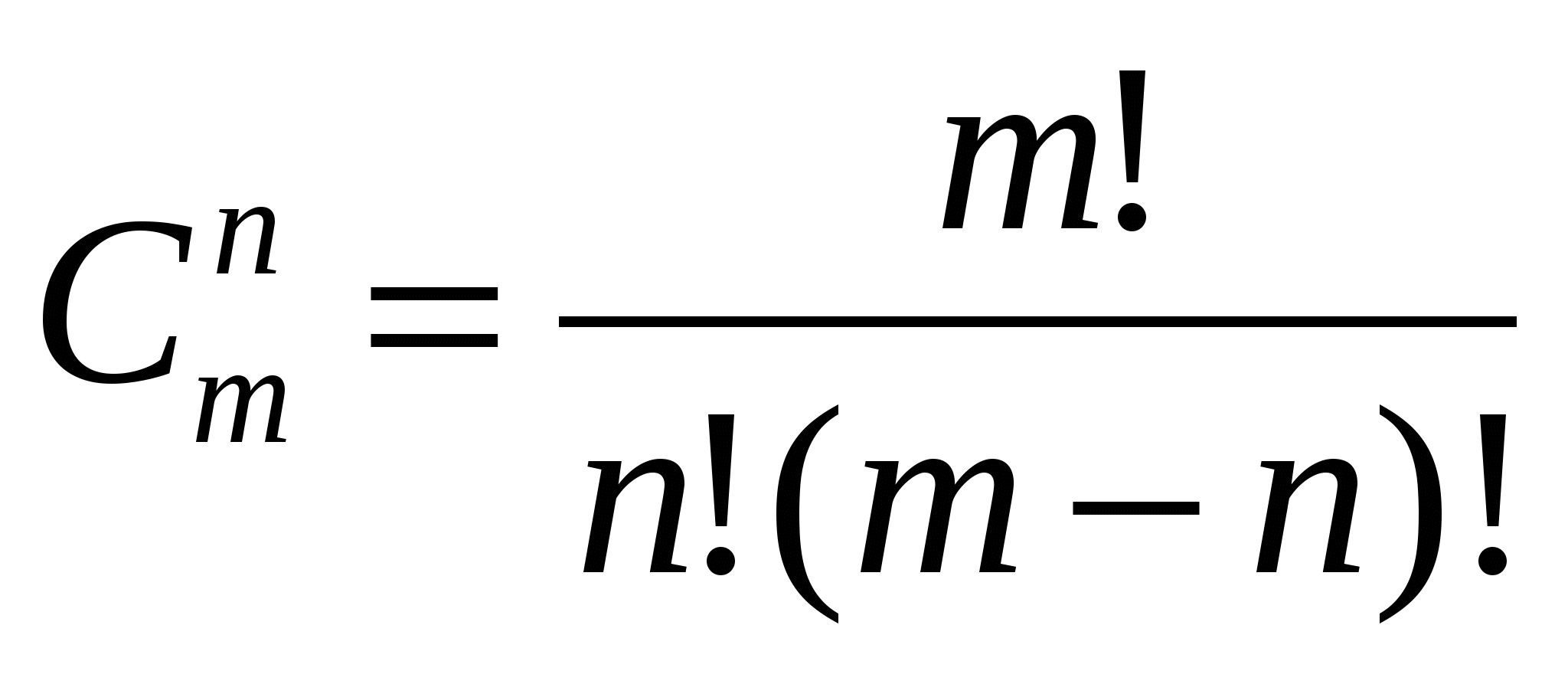
Пример 2. Решим задачу 2 с помощью этой формулы:

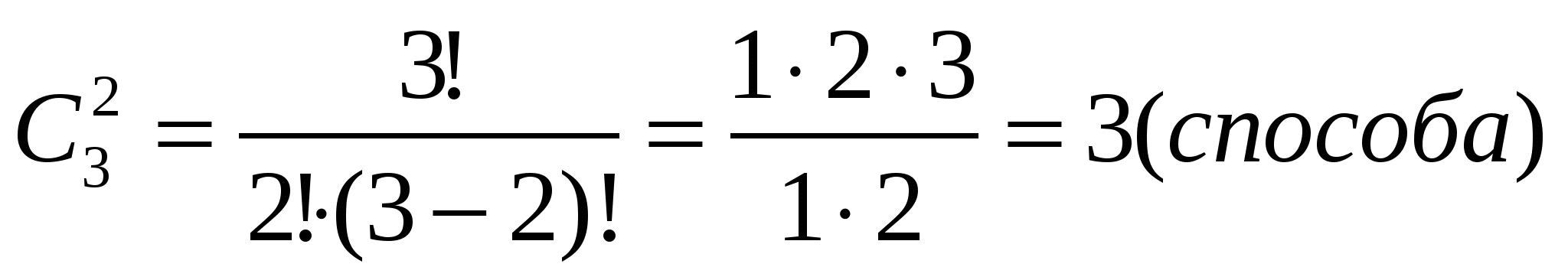
А теперь решим ту же задачу для случая m=8, n=3:

Мы рассмотрели теоретические основы комбинаторики. Теперь перейдем к этапу закрепления новых знаний при решении задач.

Закрепление материала.

Задачи для решения на закрепление нового материала. Разобрать и кратко записать решение.

Задача № 1. Сколькими способами могут быть расставлены 5 участниц финального

забега на 5-ти беговых дорожках?

Решение: Р₅= 5!= 1 ∙2 ∙3 ∙4 ∙5 = 120 способов.

Задача №2. Сколько трехзначных чисел можно составить из цифр 1,2,3, если каждая

цифра входит в изображение числа только один раз?

Решение: Число всех перестановок из трех элементов равно Р₃=3!, где 3!=1 * 2 * 3=6

Значит, существует шесть трехзначных чисел, составленных из цифр 1,2,3.

Задача № 3. Сколькими способами четверо юношей могут пригласить четырех из шести

девушек на танец?

Решение: два юноши не могут одновременно пригласить одну и ту же девушку. И

варианты, при которых одни и те же девушки танцуют с разными юношами,

считаются разными, поэтому: .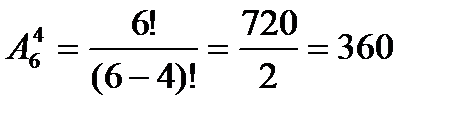

Задача № 4. Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5,

6, 7, 8, 9 при условии, что в записи числа каждая цифра используется только

один раз?

Решение: В условии задачи предложено подсчитать число всевозможных комбинаций из

трех цифр, взятых из предположенных девяти цифр, причём порядок

расположения цифр в комбинации имеет значение (например, числа 132)

и 231 различные). Иначе говоря, нужно найти число размещений из девяти

элементов по три.

По формуле числа размещений находим: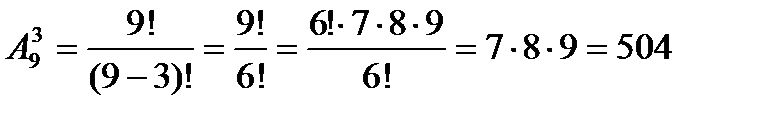

Ответ:504 трехзначных чисел.

Задача №5 Сколькими способами из 7 человек можно выбрать комиссию, состоящую из 3

человек?

Решение: Чтобы рассмотреть все возможные комиссии, нужно рассмотреть все

возможные 3 – элементные подмножества множества, состоящего из 7

человек. Искомое число способов равно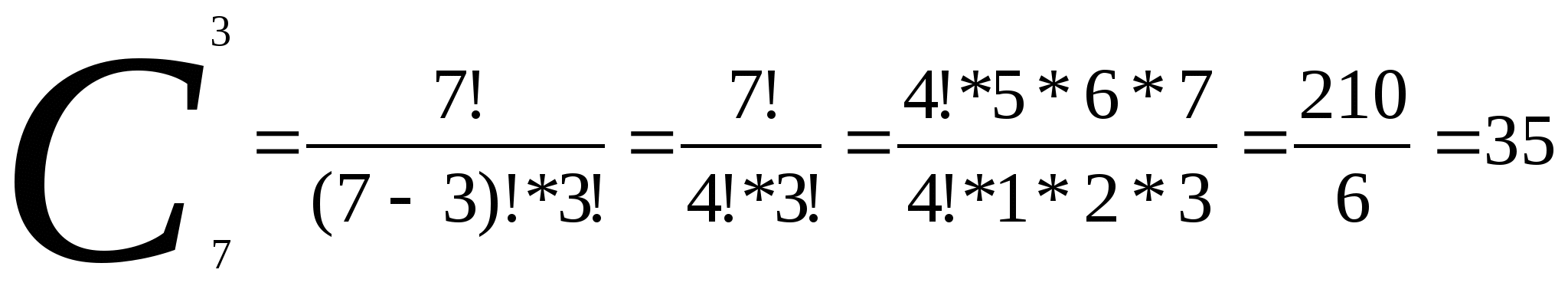

Задача № 6. В соревновании участвуют 12 команд. Сколько существует вариантов

распределения призовых (1, 2, 3) мест?

Решение: А₁₂³= 12 ∙11 ∙10 = 1320 вариантов распределения призовых мест. Ответ: 1320 вариантов.

Задача № 7. На соревнованиях по лёгкой атлетике нашу школу представляла команда из

10 спортсменов. Сколькими способами тренер может определить, кто из них

побежит в эстафете 4´100 м на первом, втором, третьем и четвёртом этапах?

Решение: Выбор из 10 по 4 с учётом порядка: 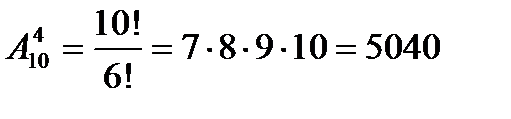способов.

Ответ: 5040 способов.

Задача № 8. Сколькими способами можно выложить в ряд красный, черный, синий и

зеленый шарики?

Решение: На первое место можно поставить любой из четырех шариков (4 способа), на

второе – любой из трех оставшихся (3 способа), на третье место – любой из

оставшихся двух (2 способа), на четвертое место – оставшийся последний шар.

Всего 4 · 3 · 2 · 1 = 24 способа.

Р₄ = 4! = 1 · 2 · 3 · 4 = 24. Ответ: 24 способа.

Задача № 9. Учащимся дали список из 10 книг, которые рекомендуется прочитать во

время каникул. Сколькими способами ученик может выбрать из них 6 книг?

Решение: Выбор 6 из 10 без учёта порядка: 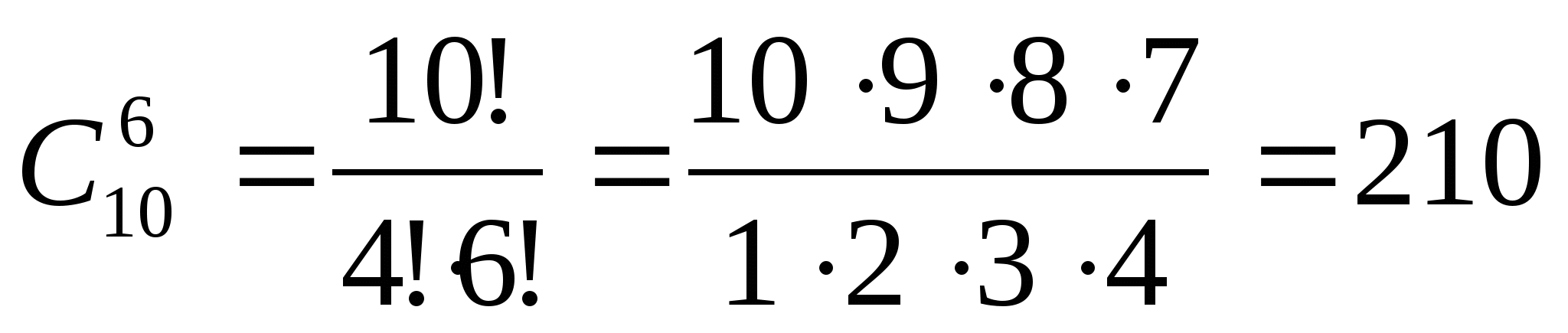способов.

Ответ: 210 способов.

Задача № 10. Девятиклассники Женя, Сережа, Коля, Наташа и Оля побежали на

перемене к теннисному столу, за которым уже шла игра. Сколькими

способами подбежавшие к столу пятеро девятиклассников могут занять

очередь для игры в настольный теннис?

Решение: Первым в очередь мог встать любой девятиклассник, вторым – любой из

оставшихся троих, третьим – любой из оставшихся двоих и четвёртым –

девятиклассник, подбежавший предпоследним, а пятым – последний. По

правилу умножения у пяти учащихся существует 5· 4×3×2×1=120 способов

занять очередь.

Вычислите.

Дата добавления: 2021-04-06; просмотров: 164; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!