Схемы выбора с возвращением (с повторением элементов)
Элементы комбинаторики
Комбинаторика (теория выборок) – раздел математики, в котором изучаются задачи выбора элементов из заданного множества и расположения их в группы по заданным правилам.
Определения
Различные группы, состоящие из каких-либо элементов и отличающиеся одна от другой либо самими элементами, либо порядком следования элементов, либо количеством повторений элементов, называются выборками.
Выборка называется упорядоченной, если существенным является не только состав элементов в ней, но и порядок их расположения.
Выборка называется неупорядоченной, если порядок следования элементов в выборке не существенен.
Пример.Дано множество, состоящее из пяти цифр 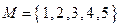 .
.
Составить выборки из пяти элементов по одному элементу: 1,2,3,4,5 – это сами элементы множества 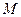 .
.
Составить выборки из пяти элементов по два элемента без повторения элементов: 12, 21, 13, 31, 14, 41, 15, 51, 23, 32, 24, 42,…
Составит выборки из пяти элементов по три элемента без повторения элементов: 123, 132, 321, 231, 124, 421, 241, 345, 543,…
Составить выборки из пяти элементов по четыре элемента без повторения элементов: 1234, 4321, 1324, 3421, 1245, 5421, 5432,…
Составить выборки из пяти элементов по пять элементов без повторения элементов: 12345, 54321, 21345, 31245, 41235,51234,…
Составить выборки из пяти элементов по три элемента с повторением элементов: 111, 221, 123, 443, 234,...
Рассмотрим различные схемы выбора элементов из множества и правила подсчета числа выборок.
Различают выборки без возвращения (при составлении выборки взятый из множества 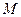 элемент не возвращается обратно) и выборки с возвращением (при составлении выборки один и тот же элемент может быть выбран несколько раз).
элемент не возвращается обратно) и выборки с возвращением (при составлении выборки один и тот же элемент может быть выбран несколько раз).
Правило умножения.
Пусть дано 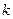 множеств
множеств 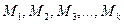 , и пусть множество
, и пусть множество 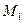 содержит
содержит 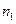 различных элементов, множество
различных элементов, множество 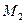 содержит
содержит 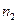 различных элементов, множество
различных элементов, множество 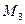 содержит
содержит 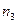 различных элементов,…., множество
различных элементов,…., множество 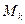 содержит
содержит 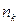 различных элементов.
различных элементов.
Выберем из каждого множества по одному элементу: 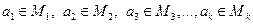 и составим из них упорядоченную выборку
и составим из них упорядоченную выборку 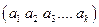 .
.
Тогда число таких выборок можно найти по формуле: 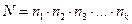 (1)
(1)
Частный случай правила умножения.
Пусть дано 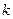 одинаковых множеств
одинаковых множеств 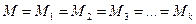 , и пусть множество
, и пусть множество 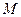 содержит
содержит 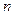 различных элементов. Выберем из каждого множества по одному элементу и составим упорядоченную выборку
различных элементов. Выберем из каждого множества по одному элементу и составим упорядоченную выборку 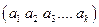 .
.
Тогда число таких выборок вычисляется по формуле: 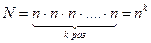 (2)
(2)
Задача 1. Сколько трехзначных целых чисел начинаются и заканчиваются нечетной цифрой?
Каждое трехзначное целое число – есть упорядоченная выборка, состоящая из трех элементов.
Первую цифру в трехзначном числе можно выбрать пятью способами (1, 3, 5, 7, 9) 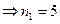 ,
,
и вторую цифру в трехзначном числе можно выбрать десятью способами (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) 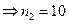 , и третью цифру в трехзначном числе можно выбрать пятью способами (1, 3, 5, 7, 9)
, и третью цифру в трехзначном числе можно выбрать пятью способами (1, 3, 5, 7, 9) 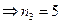 .
.
Применим правило умножения (1): 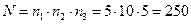 .
.
Итак, число трехзначных целых чисел, которые начинаются и заканчиваются нечетной цифрой,
равно 250.
Задача 2.
Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, если а) цифры не повторяются;
б) цифры могут повторяться?
Каждое трехзначное целое число – есть упорядоченная выборка, состоящая из трех элементов.
а) Первую цифру в трехзначном числе можно выбрать пятью способами ( 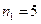 ), и для выбора второй цифры в трехзначном числе осталось четыре способа (
), и для выбора второй цифры в трехзначном числе осталось четыре способа ( 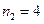 ), и третью цифру в трехзначном числе можно выбрать тремя способами (
), и третью цифру в трехзначном числе можно выбрать тремя способами ( 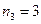 ).
).
Применим правило умножения (1): 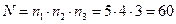
Итак, можно составить 60 трехзначных целых чисел без повторения цифр, используя цифры 1, 2, 3, 4. 5.
Например, 123, 321, 134, 453,…
в) Первую цифру в трехзначном числе можно выбрать пятью способами ( 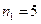 ), и вторую цифру в трехзначном числе можно выбрать пятью способами (
), и вторую цифру в трехзначном числе можно выбрать пятью способами ( 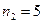 ), и третью цифру в трехзначном числе можно выбрать пятью способами (
), и третью цифру в трехзначном числе можно выбрать пятью способами ( 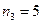 ).
).
Применим частный случай правила умножения (2): 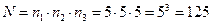
Итак, можно составить 125 трехзначных целых чисел с повторением цифр, используя цифры 1, 2, 3, 4. 5.
Например, 111, 122, 123, 223, 321, …
Задача 3. В студенческой группе 14 девушек и 6 юношей. Сколькими способами можно выбрать для выполнения различных заданий двух студентов одного пола?
По правилу умножения (1) двух девушек можно выбрать 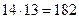 способами, а двух юношей
способами, а двух юношей 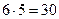 способами.
способами.
Следует выбрать двух студентов одного пола: двух девушек или двух юношей. Число таких способов выбора равно 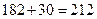 (правило сложения).
(правило сложения).
Итак, существует 212 способов выбора двух студентов одного пола для выполнения различных заданий.
Схемы выбора без возвращений (без повторения элементов)
Пусть дано множество 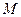 , состоящее из
, состоящее из 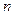 различных элементов.
различных элементов.
Размещениями из 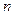 элементов по
элементов по 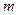 элементов
элементов 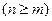 называются упорядоченные выборки, которые отличаются одна от другой либо самими элементами, либо порядком следования элементов.
называются упорядоченные выборки, которые отличаются одна от другой либо самими элементами, либо порядком следования элементов.
Число размещений из 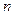 элементов по
элементов по 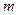 элементов обозначается
элементов обозначается 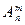 и вычисляется по формуле:
и вычисляется по формуле:
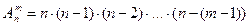 (3)
(3)
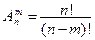 (4), где
(4), где 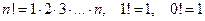 .
.
Задача 4. Сколько трехзначных целых чисел без повторения цифр можно составить из цифр 1, 2, 3, 4, 5?
Трехзначные целые числа без повторения цифр – есть упорядоченные выборки из 5 элементов по 3 элемента, которые отличаются одна от другой либо самими элементами (цифрами), либо порядком следования элементов (цифр). Такие упорядоченные выборки называются размещениями из 5 элементов по 3 элемента.
Найдем число размещений из 5 элементов по 3 элемента по формуле (3):
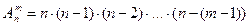
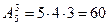
Итак, 60 трехзначных целых чисел без повторения цифр можно составить из цифр 1, 2, 3, 4, 5.
(См. задачу 2).
Задача 5. В группе 15 студентов. В профкоме на группу выделили три льготные туристические путевки в Сочи, Москву и Санкт-Петербург. Сколькими способами путевки можно распределить в группе?
Упорядоченные выборки из 15 студентов по 3 студента отличаются одна от другой либо самими студентами (в данном случае является важным, кто именно получит путевку), либо порядком следования студентов (первый выбранный студент поедет в Сочи, второй – в Москву, третий – в Санкт-Петербург).
Такие упорядоченные выборки называются размещениями из 15 элементов по 3 элемента.
Найдем число размещений из 15 элементов по 3 элемента по формуле (3):
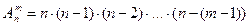
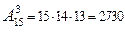
Итак, существует 2730 способов распределения трех различных путевок в группе из 15 студентов.
Перестановками из 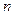 элементов по
элементов по 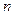 элементов называются упорядоченные выборки, которые отличаются одна от другой только порядком следования элементов.
элементов называются упорядоченные выборки, которые отличаются одна от другой только порядком следования элементов.
Число перестановок из 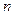 элементов обозначается
элементов обозначается 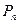 и вычисляется по формуле:
и вычисляется по формуле:  (5)
(5)
Задача 6. Сколькими способами можно расставить на полке 5 различных книг?
Упорядоченные выборки из 5 книг по 5 книг отличаются одна от другой только порядком следования книг на полке. Такие упорядоченные выборки называются перестановками по 5 элементов.
Найдем число перестановок по 5 элементов по формуле (5): 
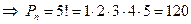
Итак, существует 120 способов расстановки 5 книг на полке.
Сочетаниями из 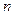 элементов по
элементов по 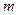 элементов
элементов 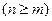 называются выборки, которые отличаются
называются выборки, которые отличаются
одна от другой хотя бы одним элементом, при этом порядок следования элементов значения не имеет
(неупорядоченные выборки).
Число сочетаний из 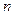 элементов по
элементов по 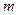 элементов обозначается
элементов обозначается 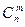 и вычисляется по формулам:
и вычисляется по формулам:
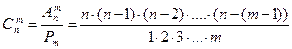 (6)
(6)
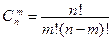 (7)
(7)
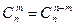 (8)
(8)
Задача 7. В группе 15 студентов. В профкоме на группу выделили три льготные туристические путевки в Санкт-Петербург. Сколькими способами путевки можно распределить в группе?
Выборки из 15 студентов по 3 студента отличаются одна от другой только самими студентами (в данном случае является важным, кто именно получит путевку), порядок следования студентов значения не имеет (каждый из выбранных студентов получит путевку в Санкт-Петербург).
Такие выборки из 15 элементов по 3 элемента называются сочетаниями из 15 элементов по 3 элемента.
Найдем число сочетаний из 15 элементов по 3 элемента по формуле (6):
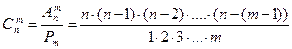
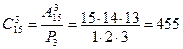
Итак, существует 455 способов распределения 3 одинаковых путевок в группе из 15 студентов.
Задача 8. Сколькими способами можно выбрать три цветка из вазы, в которой стоят 10 красных и 4 белых гвоздики? А если выбрать 1 красную гвоздику и 2 белых?
Выборки из 14 цветков по 3 цветка отличаются одна от другой только самими цветками, (порядок следования цветков значения не имеет). Такие выборки называются сочетаниями из 14 элементов по 3 элемента.
Найдем число сочетаний из 14 элементов по 3 элемента по формуле (6):
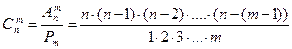
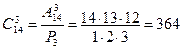
Итак, существует 364 способа собрать букет из трех гвоздик, если в вазе стоят 10 красных гвоздик и 4 белых гвоздики.
Ответим на второй вопрос задачи: выбрать одну красную гвоздику из имеющихся десяти красных гвоздик можно десятью способами 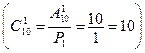 ; выбрать две белые гвоздики из имеющихся четырех белых гвоздик можно шестью способами
; выбрать две белые гвоздики из имеющихся четырех белых гвоздик можно шестью способами 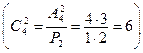 .
.
Поэтому букет из одной красной гвоздики и двух белых гвоздик можно составить 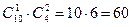
способами (правило умножения).
Схемы выбора с возвращением (с повторением элементов)
Размещения с повторениями – это упорядоченные выборки из 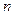 элементов по
элементов по 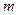 элементов, которые отличаются одна от другой самими элементами, порядком следования элементов и количеством повторений элементов (частный случай правила умножения).
элементов, которые отличаются одна от другой самими элементами, порядком следования элементов и количеством повторений элементов (частный случай правила умножения).
Число размещений с повторениями из 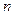 элементов по
элементов по 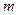 элементов вычисляется по формуле:
элементов вычисляется по формуле:
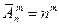 (9)
(9)
Задача 9. Сколько пятизначных целых чисел можно составить из цифр 2, 5, 7, 8?
Пятизначные целые числа, составленные из цифр 2, 5, 7, 8, отличаются друг от друга либо самими цифрами, либо порядком следования цифр, либо числом повторений цифр. Следовательно, пятизначные целые числа являются размещениями из 4 элементов по 5 элементов с повторениями элементов.
Число таких выборок найдем по формуле (9): 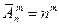
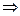
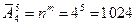
Решим эту задачу другим способом. Применим частный случай правила умножения.
Составим пятизначное целое число следующим образом: первую цифру в пятизначном числе можно выбрать 4 способами ( 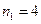 ), и вторую цифру в пятизначном числе можно выбрать 4 способами (
), и вторую цифру в пятизначном числе можно выбрать 4 способами ( 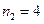 ), и третью цифру можно выбрать 4 способами (
), и третью цифру можно выбрать 4 способами ( 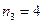 ), и четвертую цифру можно выбрать 4 способами (
), и четвертую цифру можно выбрать 4 способами ( 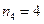 ), и пятую цифру в пятизначном числе можно выбрать 4 способами (
), и пятую цифру в пятизначном числе можно выбрать 4 способами ( 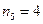 ).
).
По правилу умножения (2): 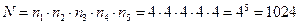
Итак, 1024 пятизначных целых чисел можно составить из цифр 2, 5, 7, 8.
Сочетания с повторениями – это выборки из 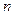 элементов по
элементов по 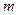 элементов, которые отличаются одна от другой самими элементами и количеством повторений элементов, при этом порядок следования элементов значения не имеет (неупорядоченные выборки).
элементов, которые отличаются одна от другой самими элементами и количеством повторений элементов, при этом порядок следования элементов значения не имеет (неупорядоченные выборки).
Число сочетаний с повторениями из 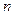 элементов по
элементов по 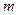 элементов вычисляется по формуле:
элементов вычисляется по формуле:
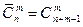 (10)
(10)
Задача 10. Сколькими способами можно составить букет из 5 цветков, если в наличии есть цветы трех сортов?
Выборки из 3 видов цветов по 5 цветков отличаются одна от другой самими цветками и количеством повторений цветков в букете, порядок следования цветков в букете значения не имеет. Такие выборки называются сочетаниями из 3 элементов по 5 элементов с повторением элементов.
Найдем число таких выборок по формуле (10):
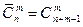
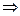
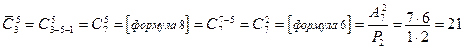
Итак, существует 21 способ составления букета из пяти цветков, если в наличии есть цветы трех сортов.
Перестановки с повторением элементов – это упорядоченные выборки по 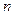 элементов, которые отличаются одна от другой порядком следования элементов и количеством повторений элементов.
элементов, которые отличаются одна от другой порядком следования элементов и количеством повторений элементов.
Пусть множество 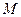 содержит
содержит 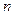 элементов. Первый элемент повторяется
элементов. Первый элемент повторяется 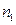 раз, второй элемент повторяется
раз, второй элемент повторяется 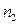 раз, …,
раз, …, 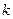 -ый элемент повторяется
-ый элемент повторяется 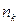 раз, то есть
раз, то есть 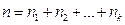 .
.
Число перестановок с повторениями из 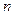 элементов вычисляется по формуле:
элементов вычисляется по формуле:
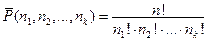 (11)
(11)
Задача 11. Сколько различных пятизначных целых чисел можно составить из цифр 3, 3, 5, 5, 8?
Пятизначные целые числа, составленные из цифр 3, 3, 5, 5, 8, отличаются друг от друга порядком следования цифр и количеством повторений цифр. Следовательно, пятизначные числа являются перестановками с повторениями из 5 элементов, где 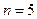 ,
, 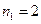 ,
, 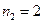 ,
, 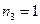 .
.
Тогда число различных пятизначных целых чисел, содержащих цифры 3, 5, 8, равно (11):
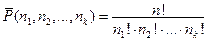
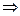
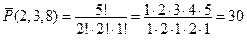 .
.
Задачи
1. Сколько четырехзначных чисел можно составить, используя цифры 1, 2, 3, 4, 5, если
а) никакая цифра не повторяется более одного раза;
б) повторение цифр допустимо;
в) числа должны быть нечетными и повторения цифр быть не может?
Ответ: 120; 625; 72.
2. Сколько двузначных целых чисел, у которых обе цифры четные?
Ответ: 20.
3. Сколько пятизначных целых чисел, которые одинаково читаются слева направо и справа налево?
Ответ: 900.
4. Кодовый замок состоит из 4 цифр. Сколько попыток может понадобиться, если код неизвестен?
Ответ: 10000.
5. Сколько можно составить четырехзначных чисел так, чтобы любые две соседние цифры были
различны?
Ответ: 6561.
6. Номер автомобиля состоит из трех букв, за которыми следует четырехзначное число. Сколько
существует автомобильных номеров?
Ответ: 197568 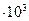
7. Сколькими способами из 20 студентов можно выбрать: а) делегацию из трех человек; б) старосту и
профорга?
Ответ: 1140, 380.
8. Группа студентов изучает 10 различных дисциплин. Сколькими способами можно составить
расписание занятий на один день, если в этот день должно быть четыре разных пары?
Ответ: 5040.
9. Из 10 мальчиков и 10 девочек спортивного класса для участия в эстафете надо составить три команды,
каждая из которых состоит из мальчика и девочки. Сколькими способами это можно сделать?
Ответ: 518400.
10. Сколькими способами 3 награды могут быть распределены между 10 участниками соревнований?
Ответ: 720.
11. В нашем распоряжении три различных флага. На флагштоке поднимается сигнал, состоящий
не менее, чем из двух флагов. Сколько различных сигналов можно поднять на флагштоке, если
порядок флагов в сигнале учитывается?
Ответ: 12.
12. Из колоды 36 карт одновременно вынимают три карты. Сколько существует различных вариантов
таких троек, если порядок следования карт в выборке значения не имеет? Сколько таких троек
содержит ровно одного туза?
Ответ: 7140; 1984.
13. Из четырех супружеских пар выбирают трех человек. Сколькими способами можно это сделать, если
а) никаких дополнительных ограничений на состав группы нет;
б) в группе должно быть две женщины и один мужчина;
в) в группе не должно быть членов одной семьи.
Ответ: 56; 24; 32.
14. В урне 12 белых и 8 черных шаров. Сколькими способами можно выбрать 5 шаров, чтобы среди
них было: а) 5 черных шаров; б) 3 белых и 2 черных шара?
Ответ: 56; 6160.
15. Игральная кость бросается три раза. Сколько существует вариантов выпадения очков в данном
опыте?
Ответ: 216.
16. В кондитерской имеется 4 вида пирожных. Сколькими способами можно составить набор из 6
пирожных?
Ответ: 84.
17. Сколько различных десятизначных чисел можно получить, используя в их написании цифры
2, 2, 3, 3, 4, 4, 4, 5, 5, 5?
Ответ: 25200.
18. Сколько «слов» можно получить, переставляя буквы в словах: а) ГОРА; б) ИНСТИТУТ?
Ответ: 24; 3360.
Дата добавления: 2021-04-05; просмотров: 202; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
