Задача 6. Плоский изгиб (консольн ая балка)
Глава 6. ПЛОСКИЙ ИЗГИБ
Расчет на прочность
Плоским (прямым) поперечным изгибом балки называется изгиб, при котором все внешние нагрузки действуют в одной из главных плоскостей инерции балки, причем проекции внешних сил и реакций опор на ось балки равны нулю. В этом случае отличны от нуля только две из шести внутренних сил: внутренняя поперечная сила Q y и внутренний изгибающий момент M z ., действующий в этой же плоскости, где приложены внешние силы (рис. 23).
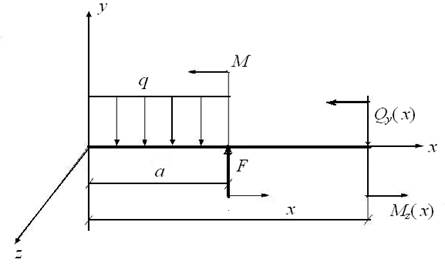
Рис. 23. Внутренние силы в поперечном сечении балки:
поперечная сила Qy(х) и изгибающий момент Mz .(х)
Эти внутренние силы определяются методом сечений из условий статического равновесия части балки, расположенной по одну сторону от рассматриваемого сечения, под действием внешней нагрузки и искомых внутренних сил, действующих со стороны отброшенной части балки. Условия статического равновесия сводятся к двум уравнениям статики: равенстве нулю суммы проекций на ось у всех сил (ΣY = 0) и равенстве нулю суммы моментов в сечении х всех сил (Σmx = 0).
Для балки (см. рис 23) поперечная сила Qy(х) и изгибающий момент Mz .(х) определяются из двух уравнений статического равновесия:
ΣY = F – q ∙ a –- Qy(х) = 0,
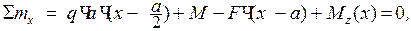
откуда
Qy(х) = F – q ∙ a, (2)
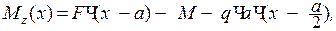 (3)
(3)
|
|
|
При выполнении условий (2) и (3) все остальные условия статического равновесия удовлетворяются автоматически, т. е. никаких других внутренних сил при плоском изгибе не возникнет.
Из (2) и (3) видим, что внутренняя поперечная сила Q y(х) в сечении x численно равна алгебраической сумме всех внешних сил, действующих по одну сторону от рассматриваемого сечения. Аналогично, внутренний изгибающий момент Mz(х) в сечении х численно равен алгебраической сумме моментов всех внешних нагрузок, действующих по одну сторону от рассматриваемого сечения.
Для того, чтобы внутренние силы определялись однозначно и независимо от того, равновесие какой части балки рассматривается, вводят правило знаков для Qy(х) и Mz(х).
Если внешняя сила (F , q) стремится повернуть рассматриваемую часть балки относительно центра тяжести сечения x по ходу часовой стрелки, то ее вклад во внутреннюю силу Q y(х) положителен, если против хода часовой стрелки – отрицателен (рис. 24).

Рис. 24. Определение знака поперечной силы Qy(х)
Если внешняя сила (F , q , M) стремится изогнуть часть балки относительно центра тяжести сечения х выпуклостью вниз (сжатое волокно сверху), то ее вклад во внутренний момент Mz(х) положителен; если выпуклостью вверх (сжатое волокно снизу) – отрицателен (рис. 25).
|
|
|

Рис. 25. Определение знака изгибающего момента Mz(х)
Направим ось абсцисс (ox) системы координат слева направо вдоль оси балки. Тогда внутренние усилия Qy(х), Mz(х) в поперечных сечениях и внешняя распределенная нагрузка q будут функциями x. Они связаны дифференциальными соотношениями:
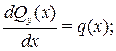 (4)
(4)
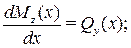 (5)
(5)
 (6)
(6)
Здесь q(х) считается положительной, если она направлена вверх. Эти соотношения следует использовать при проверке правильности построения эпюр Q y(х) и M z(х).
Внутренний изгибающий момент связан с нормальными напряжениями, которые распределяются по высоте сечения неравномерно, вызывая растяжение одной его части и сжатие другой.
Условие прочности по нормальным напряжениям для балки любой формы поперечного сечения имеет вид
|
|
|
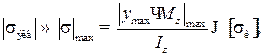 (7)
(7)
где Mz – изгибающий момент в опасном сечении балки, Н∙м;
Iz – момент инерции поперечного сечения, м4;
ymax – расстояние от нейтральной оси до наиболее удаленной точки
поперечного сечения, м.
Для балок, поперечные сечения которых симметричны относительно нейтральной оси z, условие прочности преобразуется к виду
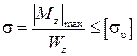 , (8)
, (8)
где Wz – осевой момент сопротивления поперечного сечения, м3.
На основании соотношений (7), (8) Wz определяется по формуле
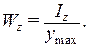
Поперечная сила Qy(х), вектор которой лежит в плоскости поперечного сечения, вызывает в точках сечения касательные напряжения τxy. По закону парности касательных напряжений на продольных площадках возникают равные им напряжения τy х = τxy = τ...
Напряжения τxy возникают вследствие деформации среза поперек продольных волокон балки, а напряжения τy х вызваны деформацией сдвига продольных волокон вдоль балки.
Для балок постоянного поперечного сечения при допущении, что касательные напряжения τ. по ширине сечения b распределены равномерно, касательные напряжения при изгибе определяются по формуле Журавского:
|
|
|
 ,
,
где 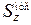 – статический момент относительно оси z отсеченной части сечения;
– статический момент относительно оси z отсеченной части сечения;
b –ширина сечения;
Iz –осевой момент инерции сечения.
Интенсивность сдвигающих усилий Т (погонная сдвигающая сила) определяется равенством
 .
.
Касательные напряжения распределяются по сечению неравномерно, достигая максимального значения на нейтральной оси. Как показывают расчеты, в балках, поперечные размеры которых много меньше их длины, касательные напряжения в поперечных сечениях значительно меньше нормальных, поэтому, если балка изготовлена из изотропного материала, то при записи условия прочности касательные напряжения можно не учитывать, именно поэтому σэкв ≈ σ.
6.1.1. Построение эпюр внутренних сил Qy и Mz
Эпюрой внутренней силы называется график ее изменения вдоль оси балки. Из определения внутренней поперечной силы Q y(х) следует, что в том и только в том сечении, где приложена внешняя сосредоточенная сила, имеется скачок на эпюре Q y(х) на величину этой силы. Аналогично из определения внутреннего изгибающего момента M z(х) следует, что в том и только в том сечении, где приложен внешний изгибающий момент, – скачок на эпюре M z(х) на величину этого момента. Под внешними силами и моментами мы подразумеваем и реакции опор.
При проверке правильности построения эпюр Q y(х) и M z(х) можно использовать табл. 6, составленную на основании дифференциальных соотношений (4) – (6). В этой таблице указана связь между знаками интенсивности распределенной нагрузки q ( x ), поперечной силы Q y(х) и характером изменения эпюр Qy(х) и M z(х) .
Таблица 6
Правила построения эпюр Qy(х) и Mz(х) , основанные
на дифференциальных зависимостях между q, Qy(х), Mz(х)
| Распреде-ленная нагрузка q, кН/м | Поперечная сила Qy, кН | Изгибающий момент Mz, кН∙м |
|
q=0
| Поперечная сила постоянна | Изгибающий момент изменяется по линейному закону |
| 0 | Момент постоянный ______ | |
| + |  Момент возрастает Момент возрастает
| |
| _ |  Момент убывает Момент убывает
| |
|
q >0
| Поперечная сила возрастает по линейному закону | Момент изменяется по закону параболы, выпуклость вниз |
| 0 | Момент принимает экстремальное значение Mmin | |
| + | Момент возрастает по закону параболы, выпуклость вниз

| |
| _ | Момент убывает по закону параболы, выпуклость вниз

| |
|
q < 0
| Поперечная сила убывает по линейному закону | Момент изменяется по закону параболы, выпуклость вверх |
| 0 | Момент принимает экстремальное значение Mmax | |
| + | Момент возрастает по закону параболы, выпуклость вверх
| |
| _ | Момент убывает по закону параболы, выпуклость вверх
|
Пример 6
Рассмотрим построение эпюр Qy(х) и Mz .(х) методом записи и исследования их уравнений на примере расчета на прочность двухопорной балки.
Необходимо построить эпюры поперечных сил Qy и изгибающих моментов Mz для двухопорной двутавровой балки (рис. 26) и подобрать размеры поперечного сечения при  200 МПа.
200 МПа.
1. Определение опорных реакций:
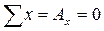 ;
;
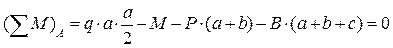 ;
;
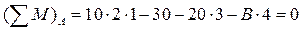 ,
, 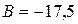 кН;
кН;
 ;
;
 ,
, 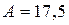 кН.
кН.
Проверка 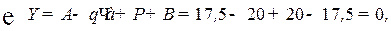 следова-тельно, реакции найдены верно.
следова-тельно, реакции найдены верно.
2. Построение эпюр Q y и M z.
Балка имеет три участка нагружения.
Участок I
В пределах первого участка произвольно намечаем сечение 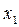
(см. рис. 26):  м.
м.
Для составления уравнений Qy(х1) и Mz(х1) рассмотрим условия равновесия левой (от сечения 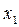 ) части балки. Поперечная сила в сечении
) части балки. Поперечная сила в сечении 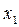 равна алгебраической сумме внешних сил по левую сторону от сечения.
равна алгебраической сумме внешних сил по левую сторону от сечения.
Учитывая правило знаков (см. рис. 24), получим Qy(х) = A – q∙x1 = = 17,5 – 10∙x1 (кН) – линейная зависимость.
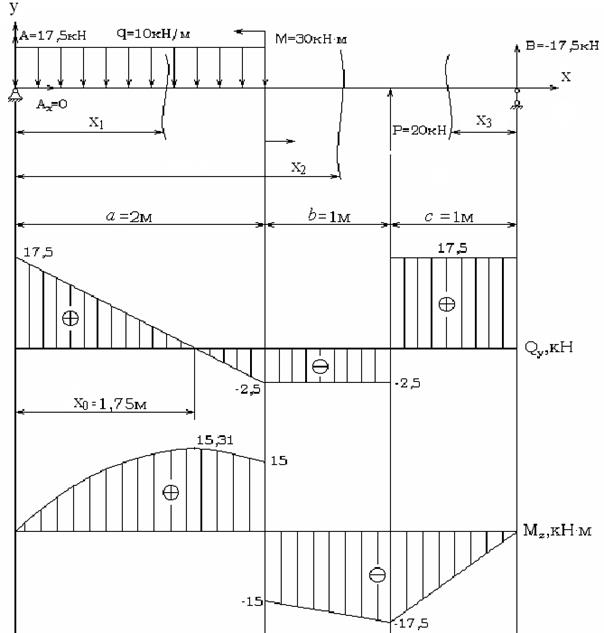
Рис. 26. Построение эпюр Qy(x) и Mz(x) для двухопорной балки
График поперечной силы Qy(х) можно построить по двум точкам, абсциссы которых соответствуют границам участка I:
Qy(0) = 17,5 кН; Qy(2) = – 2,5 кН.
Далее нам нужно найти точку пересечения эпюры с базисной линией, т. е.
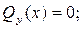
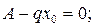
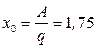 . (9)
. (9)
Внутренний изгибающий момент 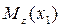 в сечении
в сечении 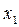 равен алгебраической сумме моментов от всех внешних нагрузок по левую сторону от сечения. С
равен алгебраической сумме моментов от всех внешних нагрузок по левую сторону от сечения. С  учетом правила знаков (см. рис. 25) получим
учетом правила знаков (см. рис. 25) получим
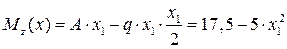 – парабола ветвями вниз. Значения на границах участка
– парабола ветвями вниз. Значения на границах участка  ,
,  кН∙м.
кН∙м. 
Вершина параболы находится из условия
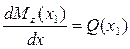 ,
,
т. е. из (9) при  м
м  кН∙м.
кН∙м.
По трем точкам строим эпюру Mz на участке I.
Участок II
Наметив сечение 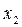 , рассмотрим левую часть балки:
, рассмотрим левую часть балки:
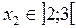 м,
м,
Qy( x 2) = A – q∙2 = 17,5 –20 = – 2,5 кН – (10)
– горизонтальная прямая, тaк как Qy( x 2) = – 2,5 кН – const.
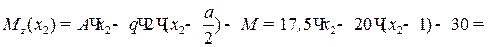 (11)
(11)
= – 2,5∙х2 – 10 кН∙м –
– прямая линия.  кН∙м,
кН∙м,  кН∙м.
кН∙м.
Можно убедиться, что из условия равновесия правой части балки
получаются те же самые выражения (10) и (11) для внутренних сил:
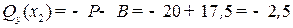 кН;
кН;

 кН∙м.
кН∙м.
Участок III
Здесь проще рассматривать условие равновесия правой части балки
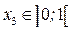 м.
м.
Учитывая правила знаков для правой части балки (см. рис. 24, 25), получим:
 – горизонтальная прямая.
– горизонтальная прямая.
 ,
,
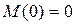 ,
,  кН∙м.
кН∙м.
Построив эпюры 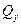 и
и  (см. рис. 26), проверяем, удовлетворяют ли
(см. рис. 26), проверяем, удовлетворяют ли
они правилам, сформулированным в табл. 6.
3. Расчет на прочность.
Условие прочности при прямом изгибе можно приближенно
записать в виде неравенства
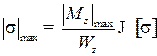 ,
,
откуда находим момент сопротивления поперечного сечения.
Вычисления производим в системе СИ:
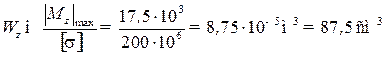 .
.
По сортаменту (см. прил. 5) определим, что такому условию соответствует двутавр № 16, Wz = 109 см3.
6.1.2. Построение эпюр внутренних сил Qy и Mz
Без записи их уравнений
Изучив закономерность изменения Qy и Mz на участках балки в зависимости от характера нагрузки, эпюры можно строить не по их уравнениям, а по отдельным ординатам, вычисленным для характерных сечений. Характерными являются сечения границ участков балки, а также сечения, где Qy меняет знак.
В отличие от способа построения эпюр, рассмотренного выше, где качественные особенности эпюр (интервалы возрастания и убывания, точки экстремумов и разрывов) выявляются только в результате их построения, а затем проверяются в соответствии с табл. 6, в данной методике эти качественные особенности используются непосредственно для построения эпюр. Как показывает практика, при этом не только уменьшается объем вычислений, но и снижается вероятность ошибки.
Рассмотрим этот метод на примере балки, представленной на рис. 26.

 1. Построение эпюры Qy
1. Построение эпюры Qy
Рисуем график эпюры в виде непрерывной линии так, что абсцисса x возрастает (идем слева направо). При этом в соответствии с правилом знаков для Qy, встретив положительную по алгебраической величине сосредоточенную силу, направленную вверх, делаем на эпюре Qy скачок вверх на величину этой силы (если сила направлена вверх, но ее значение отрицательно, то скачок вниз). Встретив силу, положительную по алгебраической величине, направленную вниз, делаем скачок вниз. Так как  то из физического смысла производной q – скорость роста функции Qy. Если на участке
то из физического смысла производной q – скорость роста функции Qy. Если на участке 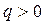 (направлена вверх), то эпюра
(направлена вверх), то эпюра  растет при увеличении x. Если
растет при увеличении x. Если 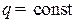 , то
, то  изображается прямой линией. Чтобы найти величину возрастания эпюры Qy на участке, нужно q умножить на длину этого участка. Соответственно, если
изображается прямой линией. Чтобы найти величину возрастания эпюры Qy на участке, нужно q умножить на длину этого участка. Соответственно, если  (направлена вниз), то
(направлена вниз), то  убывает; если
убывает; если  , то
, то 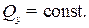
Для иллюстрации построения эпюр без записи их уравнений рассмотрим расчетную схему, приведенную на рис. 26.
Участок I
 м,
м,
 17,5 кН,
17,5 кН,
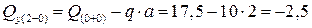 кН.
кН.
Точка, где поперечная сила Qy(x)равна нулю,
 ,
,
отсюда  м.
м.
Так как 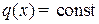 , то график
, то график  – прямая линия.
– прямая линия.
Участок II
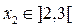 м,
м,
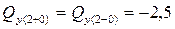 кН (скачка нет),
кН (скачка нет),
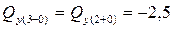 кН.
кН.
График функции 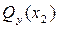 – горизонтальная прямая.
– горизонтальная прямая.
Участок III
 м,
м,
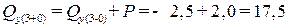 кН – скачок вверх на величину силы P;
кН – скачок вверх на величину силы P; 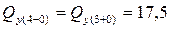 кН.
кН.
График функции  – горизонтальная прямая.
– горизонтальная прямая.
Можно считать, что балка продолжается и правее сечения x = 4 м.
Тогда все внутренние силы в сечениях x > 4 м должны быть равны нулю (из условия равновесия правой части). Проверим это:

– скачок вниз на величину силы B – проверка сошлась.
2. Построение эпюры Mz
График эпюры Mz также будем строить в порядке возрастания абсциссы x (идем слева направо). Скачки на эпюре Mz наблюдаются в тех и только в тех точках, где приложены сосредоточенные моменты сил, причем если положительный по алгебраической величине момент направлен по часовой стрелке, то в соответствии с правилом знаков (см. рис. 24, где рассматривается равновесие левой части), имеется скачок вверх на величину внешнего момента. Если встретили внешний момент, вращающий против часовой стрелки, – рисуем скачок вниз.
Так как  , то Qy(x) – скорость роста функции Mz(x). Если на участке
, то Qy(x) – скорость роста функции Mz(x). Если на участке  >0, то
>0, то 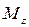
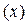 растет, при
растет, при  = 0
= 0 
Mz(x)= const;если 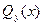 < 0, Mz(x) убывает с ростом аргумента x. В том сечении внутри участка, где Qy(x) меняет знак, на эпюре Mz(x) – экстремум. Если внутри участка Qy(x) =const,то Mz(x) – прямая; если же
< 0, Mz(x) убывает с ростом аргумента x. В том сечении внутри участка, где Qy(x) меняет знак, на эпюре Mz(x) – экстремум. Если внутри участка Qy(x) =const,то Mz(x) – прямая; если же  – наклонная прямая, то эпюра Mz(x) изображается параболой. Иначе говоря, на тех участках, где распределенная нагрузка отсутствует
– наклонная прямая, то эпюра Mz(x) изображается параболой. Иначе говоря, на тех участках, где распределенная нагрузка отсутствует 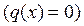 эпюра Mz(x) изображается прямой линией, а там, где
эпюра Mz(x) изображается прямой линией, а там, где 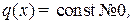 Mz(x) изображается параболой. Направление выпуклости параболы – навстречу распределенной нагрузке (рис. 27).
Mz(x) изображается параболой. Направление выпуклости параболы – навстречу распределенной нагрузке (рис. 27).
Для того, чтобы найти величину изменения внутреннего момента Mz на заданном участке, нужно среднее значение скорости изменения момента  умножить на длину участка. Иными словами, величина изменения внутреннего изгибающего момента Mz на участке равна площади эпюры Qy на этом участке:
умножить на длину участка. Иными словами, величина изменения внутреннего изгибающего момента Mz на участке равна площади эпюры Qy на этом участке:
Mzк = Mzн + Qср ∙ L, (12)
где Mzк – значение внутреннего момента в конце, а Mzн – в начале участка длиной L;
Qср – среднее значение внутренней поперечной силы на этом участке.
Формула (12) справедлива для любого участка, внутри которого нет внешних изгибающих моментов.
Участок I
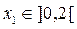 м.
м.
Так как в начале участка нет сосредоточенного момента, то  .
.
Значение момента в точке максимума (x = 1,75 м) и в конце участка вычисляем по формуле (12):
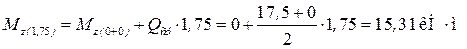 ;
;

Можно сделать проверку:
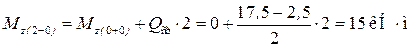 .
.
Строим параболу выпуклостью вверх.
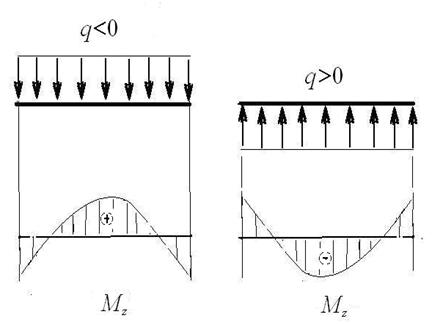
Рис. 27. Направление выпуклости параболы Mz
в зависимости от знака распределенной нагрузки q
Участок II
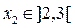 м.
м.
 – на границе I и II участков скачок вниз на величину момента М.
– на границе I и II участков скачок вниз на величину момента М.
Значение изгибающего момента в конце участка II:
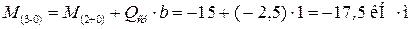
Так Qy на этом участке постоянна и отрицательна, то эпюра Mz изображается прямой линией и убывает. Строим эту прямую по двум точкам.
Участок III
 м.
м.
Так как в сечении x = 3 м нет внешнего момента, то
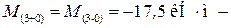 скачка нет.
скачка нет.
Так как Qy положительна и постоянна, то на эпюре Mz – рост по
прямой.
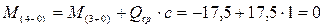 ,
,
как и должно быть из условия равновесия правой части (проверка сошлась).
Задача 6. Плоский изгиб (консольн ая балка)
Произвести расчет на прочность консольной балки. Схемы балок представлены на рис. 28, данные к задаче приведены в табл. 7. Материал балки – сталь с 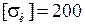 МПа.
МПа.
План решения задачи :
1) построить эпюры поперечных сил и изгибающих моментов;
2) определить диаметр круглого сечения балки или стороны прямоугольного сечения при h / b = 2.

Рис. 28. Схемы балок к задаче 6
Таблица 7
Данные к задаче 6
| Номер строки | Номер схемы | Нагрузки | Длины участков, м | |||
| F, кН | М, кН∙м | q , кН/м | а | в | ||
| 1 | I | 3 | 1 | 5,1 | 1,1 | 1,1 |
| 2 | II | 4 | 2 | 5,2 | 1,2 | 1,2 |
| 3 | III | 5 | 3 | 5,3 | 1,3 | 1,3 |
| 4 | IV | 6 | 4 | 5,4 | 1,4 | 1,4 |
| 5 | V | 7 | 5 | 5,5 | 1,5 | 1,5 |
| 6 | VI | 8 | 6 | 5,6 | 0,6 | 0,6 |
| 7 | VII | 9 | 7 | 5,7 | 0,7 | 0,7 |
| 8 | VIII | 10 | 6 | 5,8 | 0,8 | 0,8 |
| 9 | IX | 6 | 5 | 5,9 | 0,9 | 0,9 |
| 10 | X | 5 | 4 | 6,0 | 1,0 | 1,0 |
| в | а | б | в | б | в | |
Дата добавления: 2021-07-19; просмотров: 170; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
