Паросочетание max веса. Задача о назначениях. Транспорт. з-ча.
Планарные графы. Раскраски графов.
1) Нарисовать двойственный граф для графов, построить гомоморфизм из (г) на (в),
из (д) на (а) :





2) Доказать: G(p;q)–планарный и изоморфен двойственному => q=2p-2;
3) Найти хроматическое число  и хром. многочлен для графов:
и хром. многочлен для графов:
 ;
; 
4) Найти хроматический многочлен для графов: (б), (г) и (д) из п.1; а) K23


5) 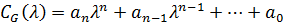 – хроматический многочлен
– хроматический многочлен
Найти: а) a0
б) 
в) an
г) an -1
6). Графы G и G1 изомрфны (f – изоморфизм). Док.:
а) для любой вершины G: deg (v) = deg (f(v));
б) G – связен ↔ G1– связен;
в) С компонента G ↔ f(С) - компонента G1;
г) G – эйлеров, гамильтонов, 2-дольн., полный ↔ G1 эйлеров, гамильтонов, 2-дольн., полный соответственно.
7) Даказать, что в план. графе существует вершина v такая, что deg (v) ≤ 5.
Комбинаторные подсчеты.
Найти:
1) Количество 4-х-значных чисел, не содержащих цифру “5”?
2) Кол. 4-х-значных чисел, содержащих хотя бы одну цифру “5”?
3) Кол. чисел от 0 до 1000, содержащих ровно одну цифру “5”?
4) Студенты профсоюза: 5 студентов 4-го курса, 7 студентов 3-го курса, 8 студентов 2-го курса, 10 студентов 1-го курса.
а) Количество способов избрания: председателя, зам. председателя, секретаря, казначея;
|
|
|
б) Пункт “а”, но председатель – студент 4-го курса;
в) Пункт “а”, но студент 4-го курса не может быть зам. председателем;
г) Пункт “а”, но студенты 1-го курса могут быть избраны только на должность секретаря.
5) Количество натуральных чисел 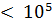 , содержащих 3, 6, 9?
, содержащих 3, 6, 9?
6) 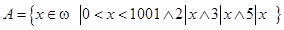 ; |А|=?
; |А|=?
7) A = { x | 1≤x≤401 ⋀ (5|x ⋁ 7|x) }, |A|=? x – нат. число.
8) x ∈ W ⋀ 0<x<10.
Сколькими способами можно разместить x так, чтобы 4 было расположено сразу после 5 ⋁ 5 после 4?
Сколько существует размещений, в которых 4 и 5 не стоят рядом?
9) Сколько существует способов вытащить из колоды из 52 карт 12 карт, содержащих 7 карт одной масти?
10) Монетку подбросили 10 раз. Сколько существует способов выпадения 4 решек и 6 орлов; не менее 3 решек?
11) Найти коэффициент при x7y3 в разложении (2x+3y)10.
12) Найти коэффициент при x4y5z3 в разложении (x+2y+3z)12.
13) Сколькими способами можно выбрать 3 набора по 6 карт в колоде из 52 карт?
14) Сколькими способами можно разместить буквы из слов: “институт”; “математика”?
15) Сколько целочисленных решений имеет уравнение:
n1 + n2 + n3 + n4 + n5 = 25
a) где ( ∀ 1≤i≤5 )ni ∈ W;
б) n1≥1; n2≥1; n3≥2; n4≥2; n5≥3 ?
|
|
|
16). S(n,m) – числа Стирл. 2 рода. Получиь рек. ф-лу для выч. S(n,m). Вычилсть:
S(n,1), S(n,n), S(n,2), S(n,m) при n<m.
17) f: A → B; |A|=n; |B|=m
Подсчитать число сюръекций из A на B. Интерпретировать в терминах размещения объектов по ящикам.
18) Множество A; |A|=n. Найти число всех отношений эквивалентности, которые могут быть определены на A.
19) Получить значение функции Эйлера от n методом включения-исключения.
20) (17) – методом включения-исключения.
21) Сколькими способами можно разместить n различных объектов в k неразличимых ящиков при условии, что ящики могут быть пустыми.
22) Сколькими способами можно разместить 12 объектов (x)в 6 ящиках (y) при условии:
а) x – различимы, y – различимы, y – могут быть пустыми;
б) x – различимы, y – различимы, y – не могут быть пустыми;
в) x – неразличимы, y – различимы, y – не могут быть пустыми;
г) x – неразличимы, y – различимы, y – могут быть пустыми;
д) x – различимы, y – неразличимы, y – могут быть пустыми;
е) x – различимы, y – неразличимы, y – не могут быть пустыми;
Потоки в сетях.
1) Найти максимальный поток в сетях:
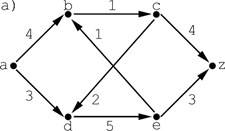


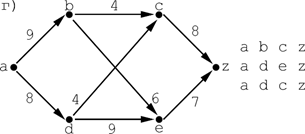
2) 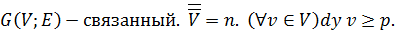 Оценить радиус,
Оценить радиус,  .
.
3) Найти поток min стоимости при заданной величине потоков: p=20: р=10; рmax.
|
|
|
а) p=20: р=10; рmax.
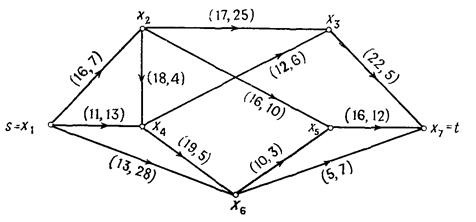
б) p=12: р=10; рmax.

Паросоч. в 2-дольном графе. Теорема Холла.
1.1) («Задача о гареме».) Обозначим через B некоторое множество юношей и предположим, что каждый юноша из B желает взять в жены более чем одну знакомую девушку. Найдите необходимые и достаточные условия существования решения этой задачи. ( Указание: замените каждого юношу несколькими тождественными ему экземплярами и примените затем теорему Холла. )
1.2) Покажите, что если каждый юноша дружит с r девушками, а каждая девушка дружит с r юношами (  ), то задача о свадьбах имеет решение; выведите отсюда, что регулярный двудольный граф обладает совершенным паросочетанием.
), то задача о свадьбах имеет решение; выведите отсюда, что регулярный двудольный граф обладает совершенным паросочетанием.
1.3) Предположим, что выполнено условие теоремы о свадьбах и что каждый из m юношей знаком по меньшей мере с t девушками; докажите индукцией по m, что супружеские пары могут быть составлены по крайней мере t ! способами, если  и по крайней мере
и по крайней мере  способами, если
способами, если 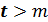 .
.
2) Найти макс. паросоч. в 2-дольн. графах:



Паросочетание max мощности.
Найти паросочетание макс. мощности в следующих графах:

|
|
|
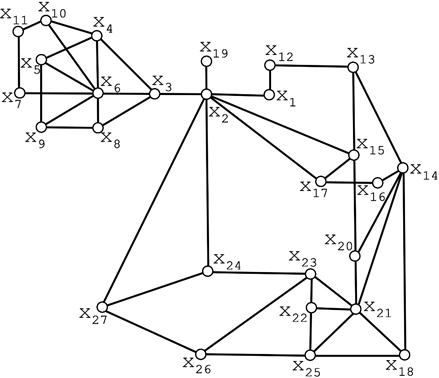
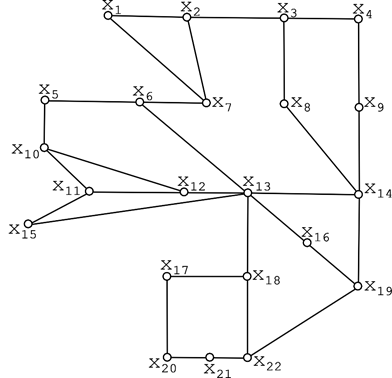
Паросочетание max веса. Задача о назначениях. Транспорт. з-ча.
1. Найти max паросочетание в гр.:

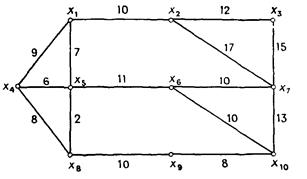
2. Решить за-чу о назначениях (венгерский алгоритм) для К88 и К66:


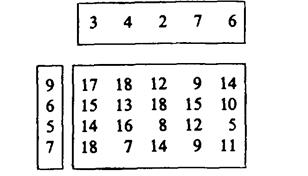
3. Решить транспорт. з-чу. α- величина предложения (источник), β- величина спроса (сток):

Дата добавления: 2021-07-19; просмотров: 172; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
