Наибольшее и наименьшее значение функции
Содержание темы «Применение производной функции»
Нахождение стационарных точек и промежутков монотонности.
Достаточный признак убывания (возрастания) функции, теорема Лагранжа, понятия «промежутки монотонности функции»
Экстремумы функции и значения в них
Определения точек максимума и минимума, необходимый признак экстремума (теорему Ферма) и достаточный признак максимума и минимума, знать определения стационарных и критических точек функции
Исследование и построение графиков функций.
Схема исследования функции, метод построения графика чётной (нечётной) функции
Нахождение наибольших и наименьших значений функций.
Алгоритм нахождения наибольшего и наименьшего значений функции на отрезке и на интервале
Основные сведения из теории
Экстремумы функции
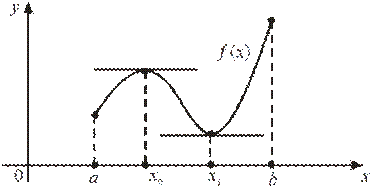
Определение: Точка х0 называется точкой максимума т. max функции f(х) если для всех х из некоторой окрестности точки х0 выполняется неравенство f(х) ≤ f(х0)
Другими словами: т. max – точка, выше которой график не поднимается
(в примере: х=4 –т.max)
Определение: Точка х0 называется точкой минимума т. min функции f(х) если для всех х из некоторой окрестности точки х0 выполняется неравенство f(х) ≥ f(х0)
Другими словами: т. min – точка, ниже которой график не опускается
(в примере: х=-1 –т.min)
Определение: Точки минимума т. min и точки максимума т. max называются точками экстремума функции.
|
|
|
Теорема Ферма: Пусть функция f(х) определена в некоторой окрестности точки х0 и дифференцируема в этой точке. Если х0 – точка экстремума функции f(х), то f′(х0)=0.
Другими словами: Необходимое условие существования точек экстремума: f′(х0)=0
 | |||
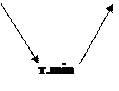 | |||
Алгоритм нахождения точек экстремума функции (т. max, т. min) :
1) Найти интервалы возрастания и убывания функции:
- Найти производную функции f′(х);
- Найти стационарные точки (точки, в которых производная f(х) равна нулю), т.е. решить уравнение f′(х)=0;
- Отметить эти точки на числовой оси, указать промежутки;
- Выявить знаки производной f′(х) на каждом из полученных промежутков (подставить любое число из проверяемого промежутка в производную и узнать знак);
- Записать ответ.
2) По схеме определить точки максимума и точки минимума.
Исследование функции с помощью производной
Алгоритм исследования функции для построения графика
1. Найти область применения функции;
2. Найти производную функции f′(х);
3. Найти стационарные точки;
4. Найти промежутки возрастания и убывания функции;
5. Определить точки экстремума (т.max, т.min);
|
|
|
6. Найти значение функции в стационарных точках;
7. Заполнить таблицу;
8. Построить график.
Наибольшее и наименьшее значение функции
Алгоритм нахождения наибольшего и наименьшего значения функции на отрезке [а;в]
1) Найти значение функции на концах отрезка, т.е. f(а), f(в);
2) Найти производную функции f′(х);
3) Найти стационарные точки (f′(х) =0)
4) Проверить входят ли стационарные точки в отрезок [а;в];
5) Найти значение функции в стационарных точках;
6) Из найденных значений выбрать наибольшее и наименьшее.
2. Примеры и упражнения
Пример 1: Найти точки экстремума функции:
f(х) = х3+6х2+4
Решение:
1) f ′(х) = (х3+6х2+4) = (х3)′+(6х2)′+(4)′= 3х2+6∙2х+0=3х2+12х
2) f′(х)=0 3х2+12х=0
х(3х+12)=0
х=0 или 3х+12=0
3х=-12
х= 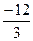
|
|
|
|





|
|

 3) f′(х) + - +
3) f′(х) + - +

 f(х)
f(х)
4) На интервале (-∞;-4) возьмём число -5, подставим в производную f′(х):
f′(-1)=3∙(-5)2+12∙(-5)=75-60=15>0, знак «+», значит (↑)
|
|
|
На интервале (-4;0) возьмём число -1, подставим в производную f′(х):
f′(-1)=3∙(-1)2+12∙(-1)=3-12=-9<0, знак «-», значит (↓)
На интервале (0;∞) возьмём число 1, подставим в производную f′(х):
f′(1)=3∙12+12∙1=3+12=15>0, знак «+», значит (↑)
5) На схеме определяем, что х=-4 т.max, х=0 – т.min
Ответ: х=-4 т.max, х=0 – т.min
Пример 2: Исследовать функцию и построить график
f(х) = 6х2-2х3
Решение:
1) Область применения: любое х;
2) f′(х) = (6х2)′-(2х3)′=6∙2х-2∙3х2=12х-6х2
3) f′(х) =0 12х-6х2=0
х(12-6х)=0
х=0 или 12-6х=0
-6х=-12
|
|
 , х=2
, х=2
4)
|
|
|
|





 f′(х) - + -
f′(х) - + -


 f(х)
f(х)
(-∞;0) «-1» f′(-1)=12∙(-1) -6∙(-1)2=-12-6=-18<0, знак «-», значит (↓)
(0;2) «1» f′(1)=12∙1-6∙12=12-6=6>0, знак «+», значит (↑)
(2;∞) «3» f′(3)=12∙3-6∙32=36-54=-18<0, знак «-», значит (↓)
5) Определим по схеме, что х=0 – т.min, х=2 – т.max
6) f(0) = 6∙02-2∙03=0-0=0
f(2) = 6∙22-2∙23=24-16=8
7) Заполним таблицу:
| х | (-∞;0) | 0 | (0;2) | 2 | (2;∞) |
| f′(х) | - | 0 | + | 0 | - |
| f(х) | 
| 0 | 
| 8 | 
|
т.min(0;0) т.max(2;8)
|
|
|
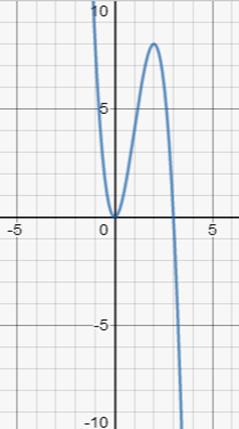
8) Строим график функции f(х) = 6х2-2х3
Пример 3: Найти наибольшее и наименьшее значение функции f(х)=2х3-3х2+2 на отрезке [-2;3]
Решение:
1) f(-2)=2∙(-2)3-3∙(-2)2+2=-16-12+2=-26
f(3)=2∙33-3∙32+2=54-27+2=29
2) f′(х) =(2х3-3х2+2)′= (2х3)′-(3х2)′+(2)′=2∙3х2-3∙2х+0=6х2-6х
3) f′(х) =0 6х2-6х =0
х(6х -6)=0
х=0 или 6х-6=0
6х=6 , х= 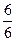
х=1
4) Получили стационарные точки х1=0, х2=1,
по заданию имеем отрезок [-2;3], х1 и х2 входят в заданный отрезок, значит обе стационарные точки нам подходят.
5) f(0)=2∙03-3∙02+2=0-0+2=2
f(1)=2∙13-3∙12+2=2-3+2=1
6) Имеем:
f(-2)= -26 f(3)= 29 f(0)=2 f(1)= 1
Выбираем самое большое и самое маленькое значение:
Наибольшее значение: f(3)= 29 , наименьшее значение: f(-2)= -26
Ответ: наибольшее значение: f(3)= 29 , наименьшее значение: f(-2)= -26
Пример 4.
Известно, что сумма двух положительных чисел равна 12. Какими должны быть эти числа, чтобы произведение их квадратов было максимальным?
Решение: прежде всего, хорошо осознаем, что от нас требуется: в условии фигурируют два положительных числа, причём ни то, ни другое мы не знаем. Но вот их сумма равна 12.
Если это, например, 2 и 10, то произведение квадратов 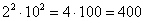 ;
;
если 7 и 5, то 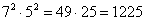 и т.д.
и т.д.
И нам нужно отыскать такую пару, для которой данное произведение будет наибольшим. Понятно, что с методом подбора тут замучаешься, к тому же искомые числа ведь могут оказаться и дробными.
Обозначим за  одно из чисел. Тогда второе число будет равно:
одно из чисел. Тогда второе число будет равно: 
Проверим, что их сумма действительно равна 12:

Теперь составим функцию произведения их квадратов:

Далее нужно найти производную, критические точки и обнаружить точку (и), в которой функция 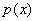 достигает максимума (если таковые, конечно, вообще существуют).
достигает максимума (если таковые, конечно, вообще существуют).
Производную здесь можно найти несколькими способами. Удобен следующий вариант: загоняем множители под единую степень и раскрываем там скобки: 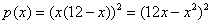 , после чего дифференцируем сложную функцию:
, после чего дифференцируем сложную функцию:
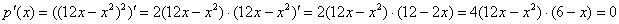
Итак, 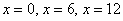 – критические точки.
– критические точки.
По условию оба числа положительны, поэтому значения 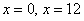 сразу исключаем из рассмотрения. Осталось проверить достаточное условие экстремума для точки
сразу исключаем из рассмотрения. Осталось проверить достаточное условие экстремума для точки 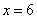 и выяснить, достигает ли там функция
и выяснить, достигает ли там функция 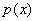 минимума либо максимума.
минимума либо максимума.
Пример 5.
Определите размеры открытого бассейна объемом 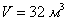 , имеющего форму прямоугольного параллелепипеда с квадратным дном, на облицовку стен и дна которого уйдет наименьшее количество материала.
, имеющего форму прямоугольного параллелепипеда с квадратным дном, на облицовку стен и дна которого уйдет наименьшее количество материала.
Решение: представили бассейн. Квадратное дно. Стены. Размеры бассейна однозначно определяются его длиной и шириной, которые в данном случае совпадают (по условию дно квадратное) и глубиной (высотой стенки). Требуется найти такие размеры бассейна, чтобы на облицовку его поверхности ушло наименьшее количество материала (например, плитки). Из чего следует, что нам нужно составить функцию суммарной площади дна и 4 стен. Изобразим на чертеже развёртку бассейна – его дно и 4 стенки, которые аккуратно лежат рядышком:
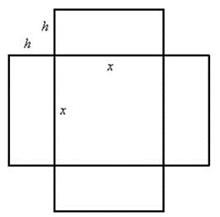
За «икс» здесь, конечно же, напрашивается обозначить сторону квадрата. Тогда площадь дна равна 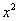 . Осталось выразить
. Осталось выразить 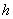 – высоту стены и найти её площадь
– высоту стены и найти её площадь 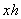 .
.
По условию, объём бассейна равняется 32 кубическим метрам. Даже не вспоминая и не разыскивая соответствующую формулу, нетрудно сообразить, что объём прямоугольного параллелепипеда – это произведение площади его «дна» на высоту:
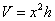
В нашем случае: 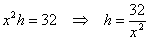 .
.
Составим функцию суммарной площади дна и четырёх одинаковых стен бассейна:
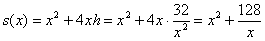
Найдем критические точки:
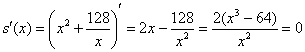
 – критическая точка.
– критическая точка.
Проверим выполнение достаточного условия экстремума:
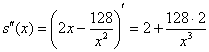
 , значит, функция
, значит, функция 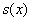 достигает минимума в точке
достигает минимума в точке 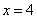 .
.
Таким образом:
сторона оптимального бассейна  ;
;
глубина 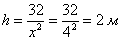 ;
;
при этом минимальная площадь облицовки:
 .
.
Ответ: сторона оптимального бассейна: 4 м, глубина: 2 м; при этом минимальная площадь облицовки 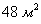 .
.
Дата добавления: 2021-07-19; просмотров: 77; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
