Несобственный интеграл 2 рода (интеграл от разрывной функции).
Интегрирование тригонометрических функций.
Для нахождения таких интегралов используют следующие приёмы:
1. Если  или
или 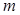 целое положительное нечётное число, то
целое положительное нечётное число, то

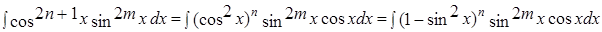
в дальнейшем раскрывая скобки и подводя под знак дифференциала получим степенные интегралы или понижаем степень тригонометрических функций по формулам:

2. Если 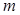 и
и  , целые, чётные, неотрицательные или
, целые, чётные, неотрицательные или  , то интеграл можно упростить с помощью формул:
, то интеграл можно упростить с помощью формул:
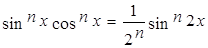
в дальнейшем необходимо понижать степень по уже известными формулами.
Задача. Вычислить.
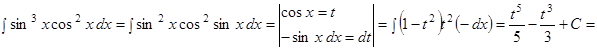

Задача. Вычислить.
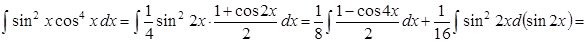
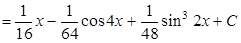
Интегралы вида 
1. Если подынтегральная функция нечётная относительно синуса, то замена  .
.
2. Если подынтегральная функция нечётная относительно косинуса, то замена 
3. Если подынтегральная функция чётная относительно косинуса и синуса, то замена 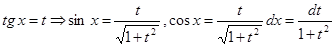
4. Если не выполняются перечисленные случаи, применяется универсальная тригонометрическая подстановка
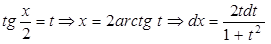 ,
, 
Задача. Вычислить.
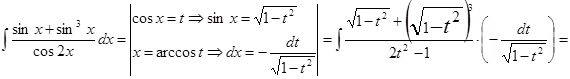


Задача. Вычислить.
1. 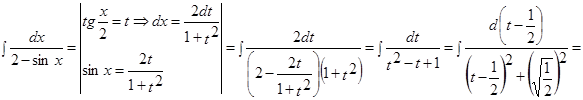

2. 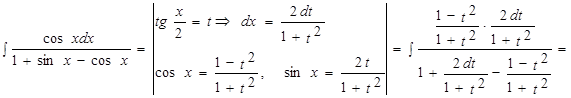
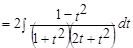
Задача. Вычислить.

Задача. Вычислить.


Тригонометрическая подстановка.
Интегралы типа 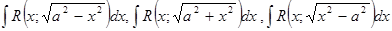 сводятся к функциям, рационально зависящим от тригонометрических
сводятся к функциям, рационально зависящим от тригонометрических
а. 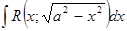 подстановкой
подстановкой 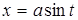 или
или 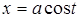 ;
;
б. 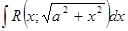 подстановкой
подстановкой 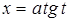 или
или  ;
;
в. 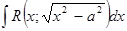 подстановкой
подстановкой  или
или 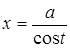 ;
;
Пример. Вычислить.
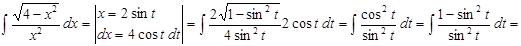
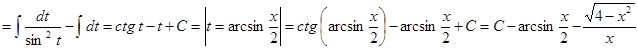
Определённый интеграл
Использование формулы Ньютона–Лейбница.
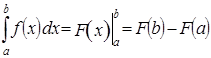
Задача. Вычислить интеграл.
|
|
|
а. 
б. 
в. 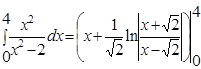
г. 
д. 
Замена переменной в определённом интеграле.
а. 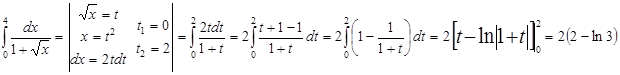
б. 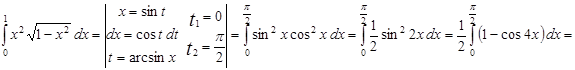
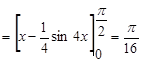
в. 
г. 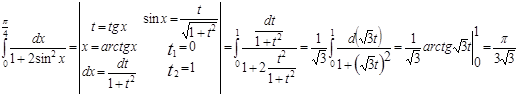
Интегрирование по частям.

Задача. Вычислить.
а. 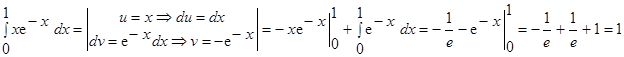
б. 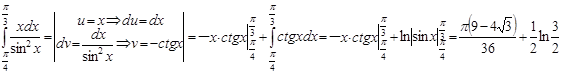
в. 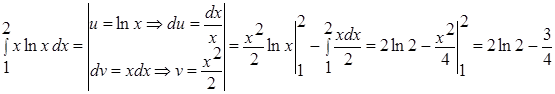
Площади плоских фигур.
а. От явно и неявно заданной функции.
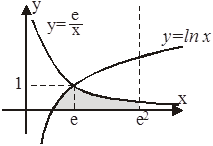 Задача . Вычислить площадь плоской фигуры ограниченной линиями
Задача . Вычислить площадь плоской фигуры ограниченной линиями 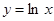 ,
, 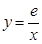 ,
, 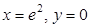 .
.
1. Методом подбора устанавливаем, что функции 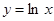 и
и 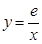 пересекаются в точке
пересекаются в точке 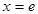 .
.
2. 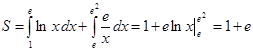
Задача. Вычислить площадь плоской фигуры ограниченной линиями  ,
, 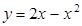 .
.
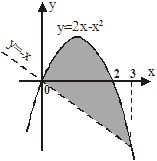 1. Найдём абсциссы точек пересечения графиков функции:
1. Найдём абсциссы точек пересечения графиков функции:

2. 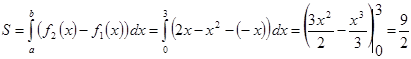
б. От функции заданной параметрически.
 Задача. Вычислить площадь плоской фигуры ограниченной астроидой
Задача. Вычислить площадь плоской фигуры ограниченной астроидой 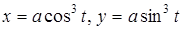 и прямой
и прямой  .
.
1. Найдём пределы интегрирования при условии, что  и
и 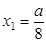 ,
, 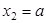 Þ
Þ 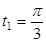 ,
,  .
.
 ,
, 
2. 


в. От функции заданной в полярной системе координат.
 Задача. Найти площадь фигуры ограниченной кардиоидой
Задача. Найти площадь фигуры ограниченной кардиоидой  и окружностью
и окружностью 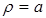
1. 
2. 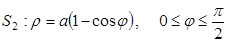
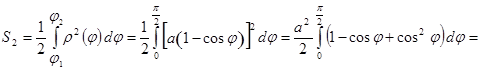

 3.
3. 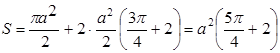
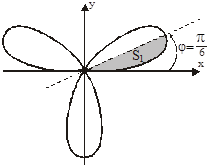
Задача. Найти площадь фигуры ограниченной трёх лепестковой розой 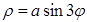 .
.
1. 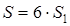
2. 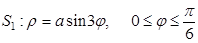
3. 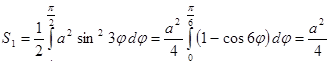
Вычисление длинны дуги плоской кривой.
а. Если кривая задана явно.

Задача. Вычислить длину дуги кривой 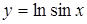 от
от 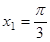 до
до 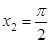 .
.
1.  ,
, 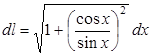
2. 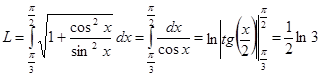
б. Если кривая задана параметрически.
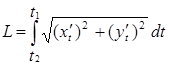
Задача. Вычислить длину дуги кривой 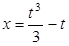 ,
, 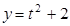 , при
, при 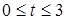 .
.
|
|
|
1. 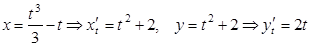 Þ
Þ 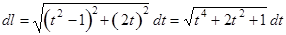
2. 
в. Если кривая задана в полярной системе координат.

Задача. Найти площадь дуги кривой от 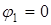 до
до 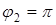 и
и 
1. 
2. 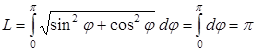
 Объем тела вращения.
Объем тела вращения.

Задача. Вычислить объём тела полученного вращением кривой 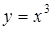 вокруг оси Ox при
вокруг оси Ox при 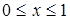 .
.
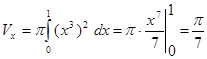
Несобственный интеграл
Интеграл с бесконечными пределами (несобственный интеграл 1 рода).
Определение. Определённый интеграл  , где промежуток интегрирования
, где промежуток интегрирования 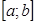 конечен, а подынтегральная функция
конечен, а подынтегральная функция 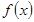 непрерывна на отрезке
непрерывна на отрезке 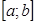 , называется собственным интегралом.
, называется собственным интегралом.
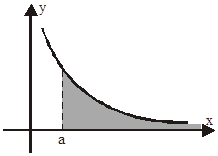 Пусть функция
Пусть функция 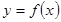 непрерывна в полубесконечном интервале
непрерывна в полубесконечном интервале 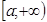 .
.
Определение. Если существует конечный предел  , то его называют несобственным интегралом 1 рода и говорят, что он сходится, если же предел не существует или равен бесконечности, то интеграл расходится.
, то его называют несобственным интегралом 1 рода и говорят, что он сходится, если же предел не существует или равен бесконечности, то интеграл расходится.

Аналогично определяется несобственный интеграл на промежутке 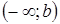
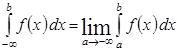
Несобственный интеграл с двумя бесконечными пределами определяется формулой
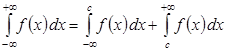
где c – произвольное число, при этом интеграл слева сходится, если сходятся оба интеграла справа, иначе он расходится.
Очевидно, что вопрос о сходимости несобственного интеграла, в геометрическом смысле, сводится к вычислению площади криволинейное трапеции с бесконечным основанием, тогда, если известна первообразная 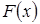 для подынтегральной функции
для подынтегральной функции 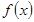 , то возможно установить сходимость несобственного интеграла с помощью формулы Ньютона – Лейбница.
, то возможно установить сходимость несобственного интеграла с помощью формулы Ньютона – Лейбница.
|
|
|
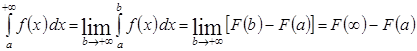
Пример. Вычислить несобственный интеграл или установить его расходимость.
а. 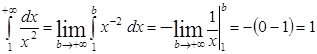
б. 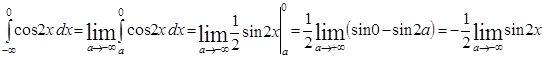
данный предел не существует, а следовательно интеграл расходится.
в. 
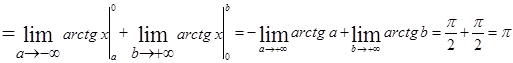
г. 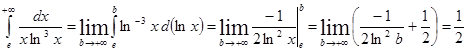
Решим вопрос о сходимости несобственного интеграла 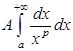 , при условии
, при условии 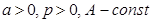 .
.
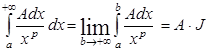
а. 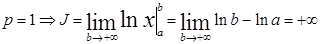 – интеграл расходится.
– интеграл расходится.
б. 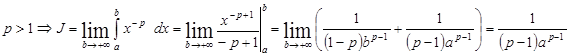
– интеграл сходится.
в. 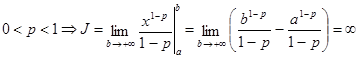 – интеграл расходится.
– интеграл расходится.
Несобственный интеграл 2 рода (интеграл от разрывной функции).
Пусть функция 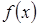 непрерывна на промежутке
непрерывна на промежутке 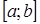 и имеет разрыв второго рода при
и имеет разрыв второго рода при  .
.
Определение. Если существует конечный предел 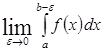 , то его называют несобственным интегралом второго рода.
, то его называют несобственным интегралом второго рода.
 Если предел, стоящий в правой части существует (не равен бесконечности), то интеграл называется сходящимся иначе расходящимся.
Если предел, стоящий в правой части существует (не равен бесконечности), то интеграл называется сходящимся иначе расходящимся.
Аналогично определяется несобственный интеграл от функции претерпевающий разрыв слева, то есть она определена при 
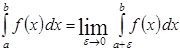
Пример. Вычислить несобственный интеграл.
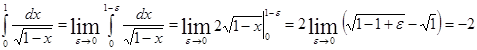
Если на интервале 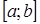 функция
функция 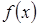 имеет несколько точек разрыва
имеет несколько точек разрыва 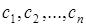 , такие, что
, такие, что  , то интеграл от такой функции сводится к несобственным интегралам второго рода.
, то интеграл от такой функции сводится к несобственным интегралам второго рода.
|
|
|
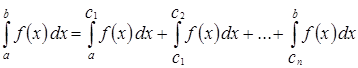
при этом интеграл в левой части сходится только в случае сходимости каждого интеграла в правой части.
Задача . Вычислить несобственный интеграл или установить его расходимость.

Задача . Вычислить несобственный интеграл или установить его расходимость.
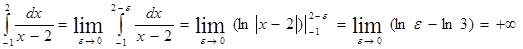 – предел не существует, а, следовательно, интеграл расходится.
– предел не существует, а, следовательно, интеграл расходится.
Задача . Исследовать на сходимость 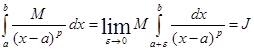
1. Если 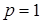 , то
, то 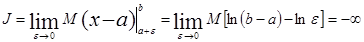 – интеграл расходится.
– интеграл расходится.
2. Если  , то
, то 
интеграл расходится.
3. Если  , то
, то 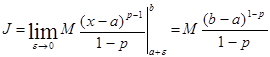 , то есть интеграл сходится.
, то есть интеграл сходится.
Дата добавления: 2021-07-19; просмотров: 75; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
