Исследовать функцию на непрерывность, найти точки разрыва, классифицировать их
НЕПРЕРЫВНОСТЬ ФУНКЦИЙ. КЛАССИФИКАЦИЯ ТОЧЕК РАЗРЫВА
Непрерывность функций. Точки разрыва
Определение 1: Функция y=f(x) непрерывна в точке х0 тогда и только тогда, когда
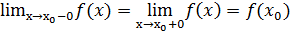 ,
,
где  и
и 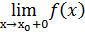 – односторонние пределы (левосторонний и правосторонний соответственно).
– односторонние пределы (левосторонний и правосторонний соответственно).
Пример 1.
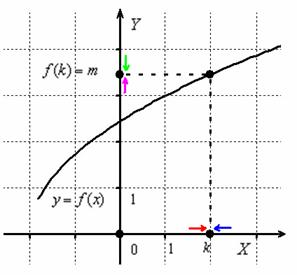
Рисунок 1 – Непрерывная функция
Рассмотрим рисунок 1. Если приближаться по оси Ох к точке k слева (х→k-0), то соответствующие значения у будут стремиться по оси Оу к точке m. Запишем левосторонний предел:

При приближении к точке k справа (х→k+0), у также стремится к значению m. Запишем правосторонний предел:
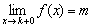
Значение функции в самой точке k равно m: f ( k )= m, следовательно, выполнены все условия непрерывности функции в точке:
1) функция определена в точке k, то есть существует значение f ( k );
2) односторонние пределы конечны и равны;
3) существует общий предел функции в точке k, равный значению функции в этой точке 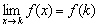 .
.
Определение 2. Функция y=f(x) непрерывна на интервале (a; b), если она непрерывна в каждой точке данного интервала.
Определение 3. Если функция y=f(x) в точке х0 не является непрерывной, то она называется разрывной в точке х0, а точка х0 – точкой разрыва функции.
Классификация точек разрыва
Определение 4. Точкой разрыва первого рода называют такую точку х0 разрыва функции, в которой существуют и конечны оба односторонних предела этой функции.
|
|
|
Определение 5. Если выполняется условие  , то точка х0 – точка устранимого разрыва.
, то точка х0 – точка устранимого разрыва.
Пример 2. Исследовать функцию 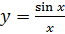 на непрерывность, найти точки разрыва, классифицировать их.
на непрерывность, найти точки разрыва, классифицировать их.
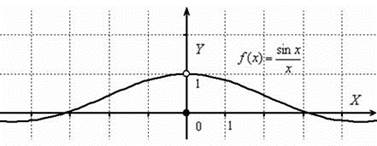
Рисунок 2 – Точка устранимого разрыва
Данная функция непрерывна на всей числовой прямой, кроме точки х=0. Функция не определена в точке х=0, а значит, терпит разрыв в данной точке.
Односторонние пределы в этой точке существуют равны:  , но не равны значению функции в точке х=0. Следовательно, в точке х=0 функция претерпевает устранимый разрыв. «Устранимый», т.к. возможно доопределить функцию в данной точке и устранить разрыв, например, таким образом:
, но не равны значению функции в точке х=0. Следовательно, в точке х=0 функция претерпевает устранимый разрыв. «Устранимый», т.к. возможно доопределить функцию в данной точке и устранить разрыв, например, таким образом:
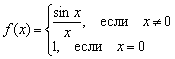
Определение 6. Если выполняется условие 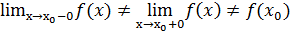 , то точка х0 – точка неустранимого разрыва. В точке х0 функция терпит разрыв первого рода со скачком.
, то точка х0 – точка неустранимого разрыва. В точке х0 функция терпит разрыв первого рода со скачком.
Пример 3. Исследовать функцию на непрерывность, найти точки разрыва, классифицировать их.
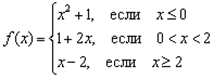
Функция y=f(x) – кусочная.
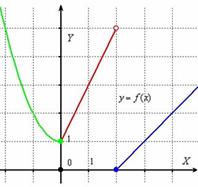
Рисунок 3 – Скачок функции
Интерес представляют точки х=0 и х=2.
Вычислив односторонние пределы при х→0, а также значение функции в данной точке, сделаем заключение, что функция непрерывна при х=0.
Исследуем точку х=2 на непрерывность:
|
|
|
1) f(2)=2-2=0 - функция определена в данной точке.
2) Вычислим односторонние пределы при х→2:
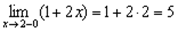
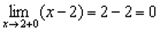
Пределы конечны, но не равны, следовательно, х=2 – точка разрыва первого рода со скачком.
Вычислим скачок:
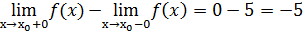
Определение 7. Точка х0 называется точкой разрыва второго рода функции y=f(x), если хотя бы один из односторонних пределов в точке х0 не существует или бесконечен.
Пример 4.
Исследовать функцию  на непрерывность, найти точки разрыва, классифицировать их.
на непрерывность, найти точки разрыва, классифицировать их.
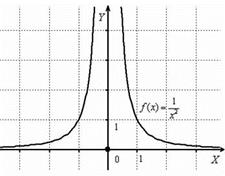
Рисунок 4 - Точка разрыва второго рода
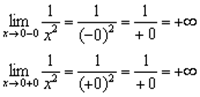 Функция не определена в точке х=0, поскольку знаменатель обращается в ноль, следовательно, функция терпит разрыв в данной точке. Классифицируем характер разрыва. Для этого вычислим односторонние пределы:
Функция не определена в точке х=0, поскольку знаменатель обращается в ноль, следовательно, функция терпит разрыв в данной точке. Классифицируем характер разрыва. Для этого вычислим односторонние пределы:
Односторонние пределы бесконечны, значит, функция  терпит разрыв второго рода в точке х=0.
терпит разрыв второго рода в точке х=0.
Практическая работа №2
Исследовать функцию на непрерывность, найти точки разрыва, классифицировать их
1. 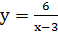
2. 
3. 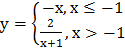
4. 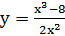
Дата добавления: 2021-07-19; просмотров: 126; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
