Свойства средней арифметической
Вопрос 3. Средние показатели
Средний показатель – показатель в форме средней величины, представляющий собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.
Средняя величина – наиболее распространенная форма статистических показателей, так как выражает типичные черты и дает общую характеристику по одному из варьирующих признаков.
Так, например, одной из задач органов государственной статистики является характеристика уровня жизни населения, в том числе в проработке по социальным группам. При этом сравнение дохода каждой семьи без подразделения на подгруппы невозможно, так как количество членов семьи, их возрастной состав, социальный статус разные. Если выполнять сравнение по социальным группам, тогда также не достигнуть объективности, так как численности по группам разные. Поэтому для характеристики уровня жизни используют только средние показатели, такие как средняя годовая заработная плата по категориям и в целом по предприятию, среднедушевой доход с выделением социального положения и другие. Средние показатели, получаемые при таком подходе, являются типичными.
Типичность средней связана с однородностью совокупности, в случае, если совокупность неоднородна, например, при определении региональной среднегодовой заработной платы служащих по предприятиям, организациям, государственным учреждениям и банкам, получают среднюю совокупность, которая будет являться фиктивной.
|
|
|
Определяется исходное соотношение средней (ИСС) по общей формуле
 .
.
Примером может служить расчет средней ставки процента по кредиту.
Средняя процентная ставка по кредитам = 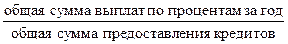 .
.
В зависимости от того, в каком виде представлены исходные данные для расчета средней, различают:
1) среднюю арифметическую;
2) среднюю гармоническую;
3) среднюю геометрическую;
4) среднюю квадратическую, кубическую и т.д.
Средняя арифметическая (  ) – наиболее распространенный вид средней. Значения признака могут быть представлены в сгруппированном и несгруппированном виде, вследствие чего и расчет средней арифметической может выполняться с использованием различных формул:
) – наиболее распространенный вид средней. Значения признака могут быть представлены в сгруппированном и несгруппированном виде, вследствие чего и расчет средней арифметической может выполняться с использованием различных формул:
1. Если значение признака представлено в исходной совокупности без группировки, расчет ведется по формуле простой (невзвешенная) средней
 ,
,
где Х i – i вариант осредняемого признака (1¸n);
n - количество единиц в совокупности.
Пример. Имеются следующие данные по цеху
Таб. номер раб. 1 2 3 4 5 6 7
Стаж раб. 10 3 5 12 11 7 9
|
|
|
Определить средний стаж рабочих.
Решение: Расчет выполняется по формуле простой средней арифметической

2. Если исходные значения признака представлены в сгруппированном виде или вариационным рядом, следует использовать формулу средней взвешенной арифметической
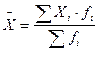 ,
,
где fi – вес i варианта.
Весы - показатель, с помощью которого несопоставимые явления приводятся в сопоставимый вид. Например, расчет средней цены материала (табл. 7).
Таблица 7
Расчет средней цены материала
| Номер партии | Цена материалов, р./т | Объем поступившей партии, т |
| 1 | 1080 | 500 |
| 2 | 1050 | 300 |
| 3 | 1145 | 1100 |
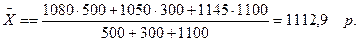
Существует следующее правило: использовать среднюю арифметическую простую (невзвешенную) можно только тогда, когда точно установлено отсутствие весов или их равенство.
Особенности расчета средней в интервальных рядах распределения
В случае, если группировка выполнена с равными интервалами, при расчете средней переходят к их серединам.
Например, распределение работников предприятий по возрасту (табл.8).
Таблица 8
Распределение работников предприятий по возрасту
| Возраст, лет | Середина интервала | Число работников, чел. |
| До 25 25-30 30-40 40-50 50-60 60 и более | 22,5 27,5 35 45 55 65 | 7 13 38 42 16 5 |
| Итого: | 121 |
|
|
|
Данная группировка выполнена с открытыми интервалами. Для определения середины интервалов границы открытых интервалов необходимо закрыть. С этой целью величины (шаг) открытых интервалов условно приравниваются к величинам интервалов, примыкающих к ним (второго и предпоследнего) и устанавливается нижняя граница первого и верхняя граница - последнего открытых интервалов.
Полученные средние значения интервала используются для расчета:

Свойства средней арифметической
1. Произведение средней на сумму частот (весов) равно сумме произведений отдельных вариантов на соответствующие им частоты (весы)
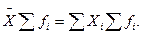
Проверить данное свойство можно, используя пример расчета средней цены за товар
1112,9·1900 =1080·500+1050·300+1145·1100.
2. Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю:
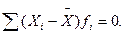
Продолжим использование примера с ценой (1080-1112,9) ·500+(1050-1112,9) ·300+(1145-1112,9) ·1100=0.
3. Если все веса уменьшить или увеличить в А раз, то средняя арифметическая не изменится.
4. Если все варианты значений признака уменьшить или увеличить в А раз, тогда значение средней также увеличится или уменьшится в А раз.
|
|
|
Следующий вид средней - средняя гармоническая. Применяется в случае, если варианты осредняемого признака (Хi) используются для расчета знаменателя при определении средней.
Таблица 9
Производительность труда по цеху «n»
| Участки цеха | Выпуск продукции, тыс. р. | Производительность труда одного рабочего, тыс. р. по участку |
| №1 №2 №3 | 140 400 180 | 14 16 12 |
| Итого: | 720 |
Определить среднюю производительность труда по цеху.
Формулы для расчета производительности труда имеют следующий вид:
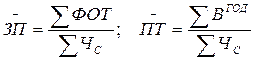
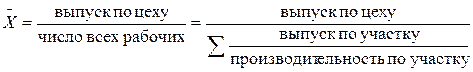
или

Расчет произведен по формуле средней гармонической взвешенной. В общем виде средняя гармоническая записывается следующим образом:
- взвешенная  , где W=Xifi;
, где W=Xifi;
- невзвешенная  .
.
Средняя геометрическая
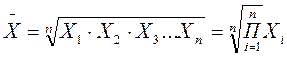
Средняя квадратическая
- невзвешенная  ;
;
- взвешенная 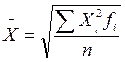 .
.
Наряду с рассмотренными средними рассчитываются так называемые структурные средние – мода и медиана.
Мода (Мо)- значение изучаемого признака, повторяющегося с наибольшей частой (или наиболее часто встречающееся значение данного признака).
Медиана (Ме) – значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности.
Главное свойство медианы – сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины
 .
.
Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности и позволяет оценить его ассимметрию. В симметричных распределениях все три характеристики совпадают.
Преимущество средних показателей моды и медианы в том, что можно определить среднее значение: 1) по несгруппированным данным и 2) в неоднородной не подчиняющейся нормальному закону распределения совокупности.
Например, рабочие бригады в количестве 9 человек, имеют тарифные разряды: 4; 3; 4; 5; 3; 3; 6; 2; 6.
Чаще встречается признак 3, следовательно, этот тарифный разряд и будет модальным, т.е. Мо=3.
Для определения медианы необходимо провести ранжирование значений признака
2 3 3 3 4 4 5 6 6
1 2 3 4 5 6 7 8 9
Центральным в этом ряду является рабочий с порядковым номером 5, имеющий 4 разряд. Следовательно, этот разряд и будет медианой Ме = 4.
Расчет среднего разряда, выполненный по формуле простой средней арифметической, даст следующий результат:
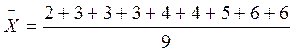 = 4.
= 4.
В рассмотренном примере структурная средняя Ме совпадает со средней арифметической, из чего можно сделать вывод об однородности совокупности и типичности рассчитанной средней.
Если ранжированный ряд включает четное число единиц, то Ме определяется как средняя из двух центральных значений.
Например, необходимо дать характеристику среднего дохода группы людей, насчитывающей 100 человек, из которых 99 человек имеют доходы в интервале от 100 до 200 долларов в месяц, доход последнего (сотого) составляет 50 тыс.долларов в мес (табл.10).
Таблица 10
Характеристика среднего дохода населения
| № п/п | 1 | 2 | 3 | 4 | … | 50 | 51 | … | 99 | 100 |
| Доход, доллары | 100 | 104 | 104 | 107 | 162 | 164 | 200 | 50000 |
Средняя, рассчитанная по формуле простой средней арифметической, дает результат (650 долларов), имеющий мало общего с доходами основной части исследуемой группы. Поэтому в расчетах средней следует переходить к структурным средним (моде и медиане).
Медиана в совокупности равна Ме=163 доллара. Расчет выполняется по двум центральным значениям признака, т.е.  =163. Полученный результат дает объективную характеристику уровня доходов 99% данной группы.
=163. Полученный результат дает объективную характеристику уровня доходов 99% данной группы.
Определение моды и медианы в интервальных рядах распределения.
В интервальных рядах с равными интервалами мода определяется:
Мо=ХМо+hМо 
где ХМо – начальное значение интервала, содержащего моду;
hМо – величина модального интервала;
 – частота модального интервала;
– частота модального интервала;
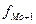 – частота интервала, следующего за модальным;
– частота интервала, следующего за модальным;
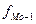 – частота интервала, предшествующего модальному.
– частота интервала, предшествующего модальному.
В интервальных рядах с равными интервалами медиана определяется:
Ме=ХМе+hМе 
где ХМе – начальное значение интервала, содержащего медиану;
hМе – величина медианного интервала;
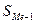 – сумма накопленных частот, предшествующих медианному интервалу
– сумма накопленных частот, предшествующих медианному интервалу
Медианным называется интервал, накопленная частота которого составляет больше половины суммы частот (> 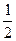
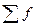 ).
).
Моду и медиану в интервальном ряду можно определить и графическим методом, путем построения гистограммы и кумуляты.
Мода определяется по гистограмме распределения.
Медиана рассчитывается по кумуляте.
Дата добавления: 2021-04-05; просмотров: 179; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
