Задача 3 (вписанный четырехугольник).

На гипотенузу АВ прямоугольного ΔАВС опустили высоту СН. Из точки Н на катеты опустили перпендикуляры НК и НЕ

а) Доказать, что точки А, В, К и Е лежат на одной окружности,

б) Найти радиус этой окружности, если АВ=12, СН=5.

Повторить. Свойство вписанного четырехугольника: сумма противоположных углов равна 180°, справедливо и обратное.

Решение

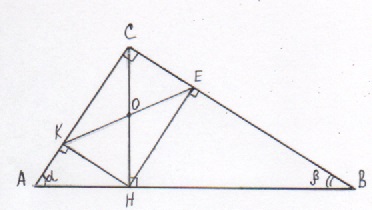
а) Если точки А, В, К и Е лежат на одной окружности, то четырехугольник АВКЕ – вписанный.

1) Пусть угол А равен α, угол В равен β, тогда α+β=90°. Используя свойство прямоугольного треугольника (сумма острых углов равна 90°) и далее в ΔАСН, ΔКСН, ΔСНВ и ΔСНЕ, получим

2) Четырехугольник КСЕН – прямоугольник, поэтому его диагонали равны и точкой пересечения делятся пополам. Значит, ΔОНЕ и ΔОНК равнобедренные ∠ОКН=∠ОНК=α, ∠ОНЕ=∠ОЕН=β (как углы при основании).

3) В четырехугольнике АКЕВ: ∠А+∠КЕВ=α+90°+β=180°, ∠B+∠АКЕ= α+90°+β=180°. Значит, около АКЕВ можно описать окружность. Пункт а) доказан.

б) 1) Нарисуем окружность. Проведем АR перпендикулярно АВ, точка R принадлежит окружности. Угол RAB равен 90° - вписанный, поэтому опирается на диаметр окружности RB.

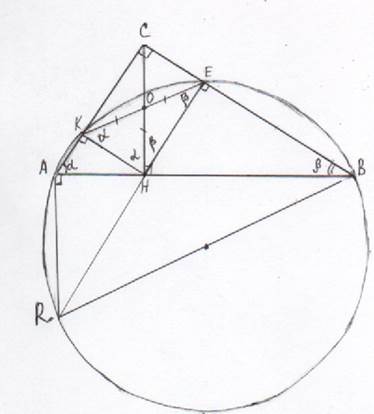
Угол НЕВ равен 90°, поэтому точки R, H и Е лежат на одной прямой

2) АСHR – параллелограмм, противоположные стороны его равны. AR=CH=5

3) По теореме Пифагора из ΔARB получим, что BR= 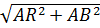= =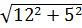13. Значит R_окр=0,5 ВК=6,5

Другой способ нахождения радиуса окружности: из ΔАСВ найти угол α, его катеты и АЕ. В ΔАКЕ ∠АКЕ=90°+α. Треугольник АКЕ вписанный в данную окружность. По следствию из теоремы синусов 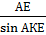=2R

Ответ: 6,5.

Задача 4 (описанный четырехугольник).

В равнобедренную трапецию АВСD с основаниями AD и ВС вписана окружность, СН – высота трапеции.

а) Доказать, что центр окружности, вписанной в трапецию, лежит на отрезке ВН.

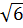б) Найдите диагональ АС, если известно, что средняя линия трапеции равна

, а угол AOD равен 135°, где О – центр окружности, вписанной в трапецию, AD – большее основание.

Решение.

а) 1) Пусть точки K и L – точки касания окружности оснований трапеции, тогда

ОК = ОL = r_впис

2) ΔBOK=ΔHOL по катету(см. пункт 1) и острому углу (углы OBK и LHO равны как накрест лежащие при BC II AD и секущей BH. Поэтому ВО = ОН.

3) Центр вписанной в трапецию окружности лежит на пересечении биссектрис внутренних углов трапеции. Данная трапеция ABCD – равнобедренная, поэтому углы ОВК и ОСК равны. Значит, треугольники ΔВОК и ΔСОК равны (по катету и острому углу)

4) Из 2) и 3) следует, что ВО=ОС=ОН. Точка О равноудалена от вершин прямоугольного треугольника ΔВСН. О – центр описанной около треугольника окружности. Следовательно О принадлежит ВН (его середина). Пункт а) доказан.

б) Для доказательства пункта б) сделаем дополнительный чертеж

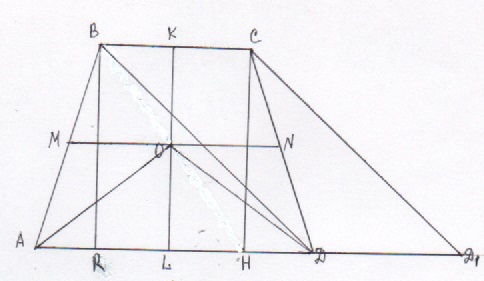
1) Пусть MN – средняя линия трапеции. Точка О принадлежит MN и О – её середина, поэтому МО =

2) АО – биссектриса, углы МАО и RAO равны, углы RAO и МОА раны как накрест лежащие. ΔАМО – равнобедренный, АМ=МО= . Тогда АВ = 2АМ=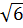

3) ∠AOD=135° (по условию), ∠OAD+∠ODA=45°. Значит, ∠BAD=∠CDA=45°. Пусть BR перпендикулярен AD. BR = AR=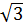

4) Пусть CD₁ II BD и точка D₁ лежит на прямой AD. Четырехугольник ВСD₁D – параллелограмм. CD₁=BD (противоположные стороны), BD=AC(диагонали равнобедренной трапеции). Тогда СD₁=BD=AC.

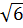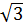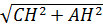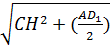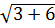5) ₁ – равнобедренный, AD₁ – основание. АD₁=AD+DD₁=AD+BC=2MN=2 . CH=BR= . По теореме Пифагора из ΔCHА: AC= = ²= = 3

Ответ: АС = 3.

Задача 5

В треугольнике АВС угол ВАС равен 60^°, угол АВС равен 45^°. Продолжения высот треугольника АВС пересекают описанную около него окружность в точках M, N, P.

а) Докажите, что треугольник MNP прямоугольный.

б) Найдите площадь треугольника MNP, если ВС=12.

Повторить. Свойство вписанных углов; теорему синусов.

Решение.

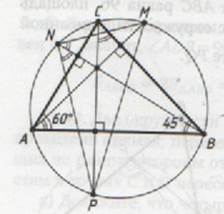а) Пусть продолжения высот треугольника АВС, проведенных из вершин А, В и С, пересекают описанную около него окружность в точках M, N и P соответственно.

Тогда вписанные углы PNB и PCB опираются на одну и ту же дугу, поэтому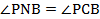

Аналогично,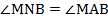

Значит,

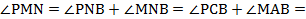
Следовательно, треугольник MNP прямоугольный. Пункт а) доказан.

б) Угол MNA равен углу NBA , угол APM равен углу ACP (вписанные углы, опирающиеся на одну дугу).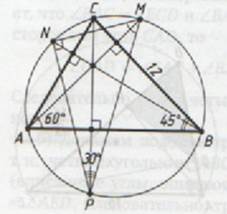

Тогда

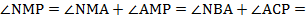
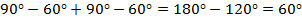
Следовательно, 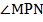= 30^°.

Пусть R – радиус описанной окружности треугольника АВС. По теореме синусов

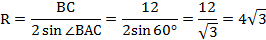
Тогда

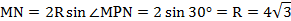
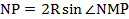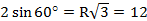
Следовательно,

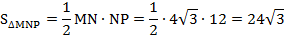
Ответ: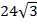

Заключение.

Выше разобранные задачи естественно не исчерпывают все возможные типы задач №18, которые могут быть предложены на экзамене. Показаны отдельные методические приемы решения планиметрических задач повышенной сложности, которые могут быть использованы учителями математики при подготовке учащихся к успешной сдачи ЕГЭ.

Источники:

1. Учебно-методические материалы для председателей и членов региональных предметных комиссий по проверке выполнения заданий с развернутым ответом экзаменационных работ ЕГЭ 2014 года. ФИПИ.

2. Гордин Р.К. ЕГЭ 2014. Математика. Решение задачи С4. - 3-е изд. доп. – М.: МЦНМО, 2014. – 448 с.

3. Прокофьев А.А., Корянов А.Г. Математика. Подготовка к ЕГЭ: решение планиметрических задач (С4). – Ростов-на-Дону, Легион, 2014. – 208 с. – (Готовимся к ЕГЭ.).

4. Прокофьев А.А., Корянов А.Г. Готовим к ЕГЭ хорошистов и отличников. Лекции 5–8

http://4ege.ru/metamatika-teoriya/3797-zadanie-s4.html
http://www.egetrener.ru/treningC4.php

Дата добавления: 2021-07-19; просмотров: 153; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 23

Мы поможем в написании ваших работ!