Количество информации и энтропия
Компромис – качество нахождения ошибок и избыточность ошибокъ
 На линию связи приходят ошибки и какой бы она не была хорошей там присутствуют ошибки. На компакт диске например будут ошибки с вероятностью 10^-4. Если пробьем в диске дырку до 8мм то он должен продолжить производить данные боз ошибок - но наши устройства защищены от чтения такой ерунды и не сработают – зато какую помехоустойчивую защиту сделали производители диска!
На линию связи приходят ошибки и какой бы она не была хорошей там присутствуют ошибки. На компакт диске например будут ошибки с вероятностью 10^-4. Если пробьем в диске дырку до 8мм то он должен продолжить производить данные боз ошибок - но наши устройства защищены от чтения такой ерунды и не сработают – зато какую помехоустойчивую защиту сделали производители диска!
Непреднамереные – ошибки среды (радиостанция + вайфай + мусор в эфире). Преднамереные ошибки – связь на войне, противник не может подслушать но может на этой волне пустить шум-сигнал который заглушит сигнал.
Сигнал не прерывный по времени и амплитуде – аналоговый сигнал. Дискретный по времени (t), Цифровой(А) (цифровое значение)

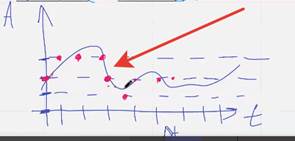 Это помеха
Это помеха
Ошибка когда 0 превратился в 1
Помеха – искажение которое передает по непрерывной линии связи
ВТОРАЯ ПОЛОВИНА ЛЕКЦИИ
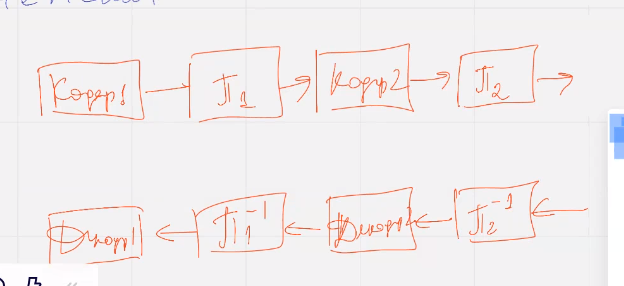
Можем ли мы поменять их местами (декодеры)?

Получается что сначала убираем помехи а потом разбираем источник, а иначе есть вариант повредить данные. Сжимаем убирая лишнее + помехоустойчивое.
Криптография – защита данных
Желтое – место для алгоритмов шифрования 
Важным является скорость работы поэтому к алгоритмам предъявляется требование по времени (Скорость алгоритм сжатия и помехоустойчивого). Существуют и долгие алгоритмы, быстрый кодер - долгий декодер, для очень важных данных которые будут сильно зашумлены (космо отрасль напр)
|
|
|
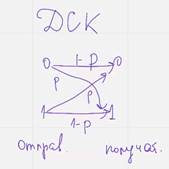 Простые модели каналов
Простые модели каналов
ДСК двоично семеричный канал (Вероятность ошибки Р, обратная вероятность 1 минус р; )( р+(1-р) = 1) Практически не существует каналов с такой работой но для теор вычислений норм.
 Мощный сигнал с земли и слабый от спутника
Мощный сигнал с земли и слабый от спутника
 Q-ичный канал связи
Q-ичный канал связи
ДСК то стиранием

Тета – знак стирания. Ее проще определить как ошибку – тут что-то случилось, место ошибки уже знаете. Стирание проще исправлять чем ошибки.
Источник сообщений ☹
Х – некоторое дискретное множество содерж кон кол-во элементов (Х – Алфавит, х -буквы и символы)
Р(х) вероятность появления события х
Сумма Хi это единица

Алфавит Х в совокупности с распределением вероятностей называется вероятностной схемой или вероятностным ансамблем.
Назовем простейшим дискретным источником без памяти Х некотрое устройство, котрое в каждый фиксированный момент времени i выдает символ xi с вероятностью pi , выборки символов происходят независимо друг от друга. (грубо говоря выдает случайные значения)
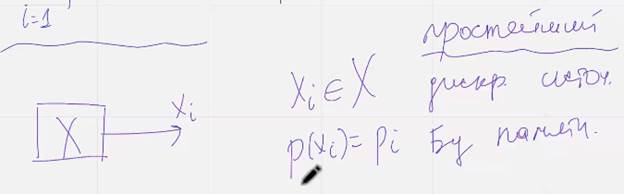
Русская речь – осмысленный набор звуков, например после ш мы не говорим ы (шы) или (шъ) т.е это НЕ пример ПДИБП
|
|
|
Количество информации и энтропия
Аксиомы для определения кол-ва информации
1. Информация одиночного события xi происходящего с вероятностью pi имеет не отрицательное значение 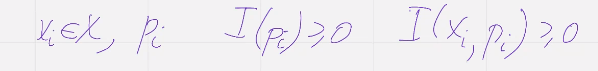
Чем реже происходит событие тем больше информации оно несет (Солнце не встало) 
2. Информация является непрерывной функцией от вероятности события 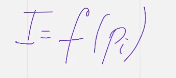
3. Совместная информация двух независимых событий xi xj с совместной вероятностью рi * pj равна сумме их информаций (См скриншот) 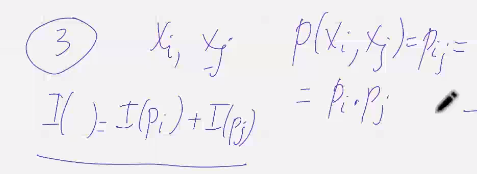
Кол- во информации события xi события pi вычисляется по формуле 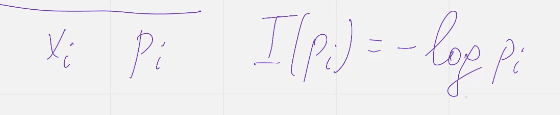
16.09.2020 ТИ
Разность между максимальной емкостью источника и энтропией н от х 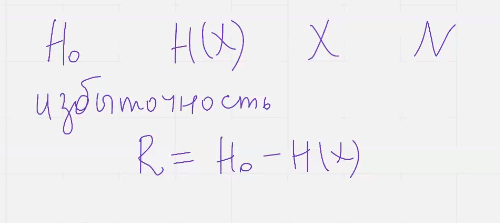 называется избыточностью источника
называется избыточностью источника
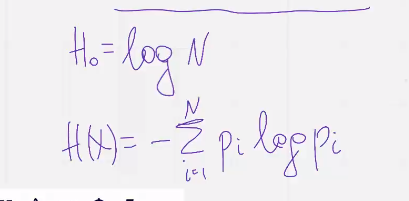
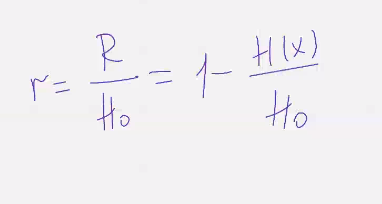 относительная избыточность
относительная избыточность


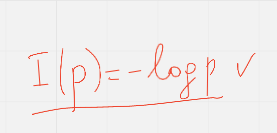 повтор формулы
повтор формулы
Помехоустойчивое, берет 0 1 и добавляем их с избытком  и делаем вывод (в нашем случае что передана единичка)
и делаем вывод (в нашем случае что передана единичка)
Кодом будет называть правило, по которому каждому информационному сообщению ставится в соответствие кодовое слово. Обратный процесс называется декодированием
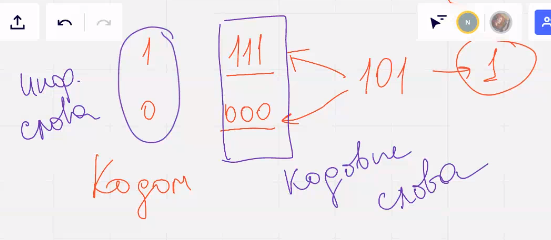
Существует большое кол-во различных помехоустойчивых кодов, различающихся избыточностью вносимой в данные, обнаруж и исправляющей способностью, сложностью алгоритмов кодирования и декодирования, требованиями к системным характеристикам аппаратуры их реализующих
|
|
|
Более того в помехоустойчивом кодировании можно различать не только коды, но и алгоритмы кодирования и декодирования.
Для одного и того же кода может быть несколько алгоритмов кодирования и несколько алгоритмов декодирования, причем специальные алгоритмы декодирования, могут в некоторых случаях увеличивать способности кода по исправлению ошибок
Подбор помехоустойчивого кода конкретному каналу связи является сложной многокритериальной задачей.
Желаемые свойства помехоустойчивых кодов:

· Исправление макс кол ва ошибок
· Минимальная избыточность кода
· Простота алгоритмов кодирования и декодирования
Подходящие варианты
· Н-крат повтор
· Код пров на четность 
· ? (потом покажут)
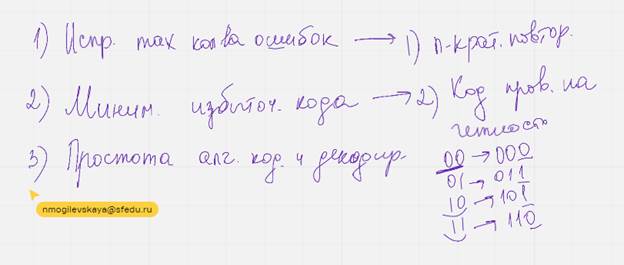
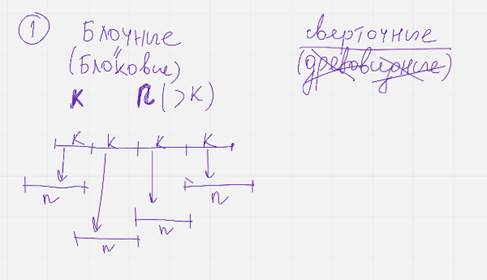
Классификация кодов
Помехоустойчивые коды можно классифицировать по различным признакам
1. По способу восприятия входной последовательности символов (Блочные (блоковые) / Сверточные)
Кодер блочного кода можно представить как устройство без памяти на вход которого поступают инф сообщения длиной К символов, а на выходе отображаются N>k кодовых символов
|
|
|
На регистры сдвига поступает входной символ суммируется в суммматоре и пормируется выходной в 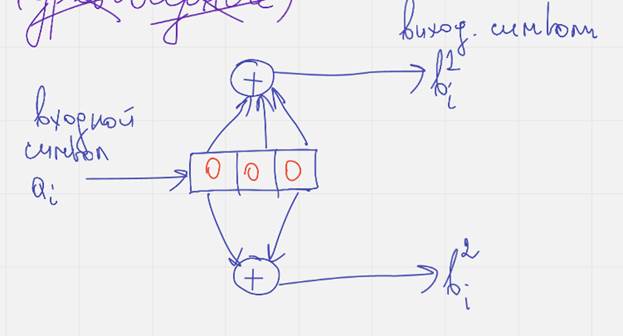
Изначально считаем что кодер заполнен нулями
Заведем доп табличку

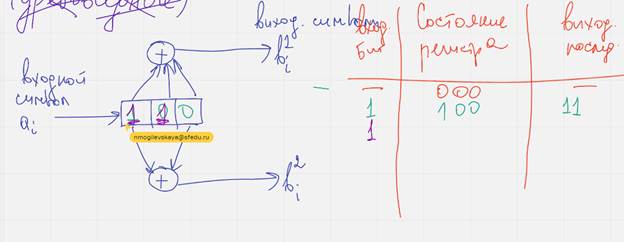
Этот кодер с памятью
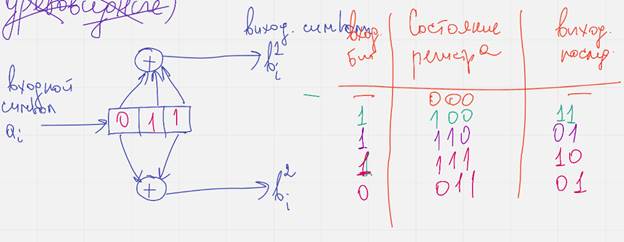
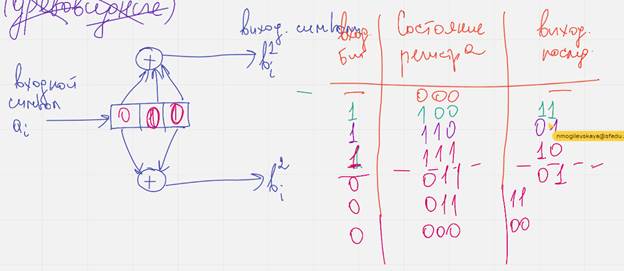
Сверточный кодер обычно представляет собой регистр сдвига, ячейки которого заполнены нулями перед началом работы, в каждый момент времени на вход регистра поступает один символ, при этом символы заполняющие регистр сдвигаются вправо на один бит. Самый правый бит выталкивается из регистра и больше не используется, результат кодирования записывается как последовательность значений образующихся на выходах сумматора. Сумматоры обычно исп. двоичную арифметику
2 . Коды можно классифицировать по мощности q алфавита над которым задан код. (Двоичные/недвоичные)
3. В зависимости от воздействия на ошибки в кодовом слове, коды разделяются на коды обнаруживающие ошибки(контрольные суммы) и исправляющие ошибки.
4.В зависимости от структуры кода выделяют линейные и нелинейные коды общим свойством является то что результатом любой линейной операции над двумя кодовыми словами является кодовое слово. (лин мы использ, но не лин лучше – быстрее, но меньше испр ошибок)

Графическая интерпретация линейных блочных кодов
Под метрическим пространством понимают множество М в котором определена функция расстояния между элементами пространства, такая что 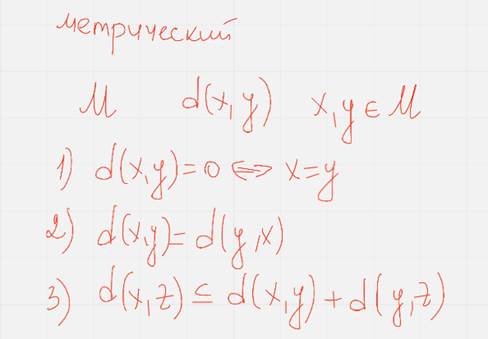
Пусть х множество из q элементов, а мн во X^n содержит все возможные векторы длинной n из элементов ин ва х  расстоянием Хемминга между элементами х у называется число несовпадающих позиций в х и у
расстоянием Хемминга между элементами х у называется число несовпадающих позиций в х и у 
Пример
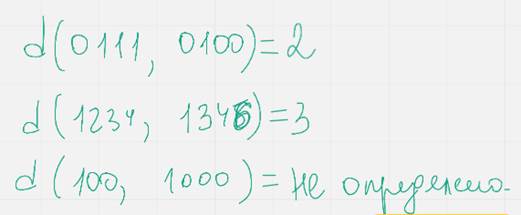

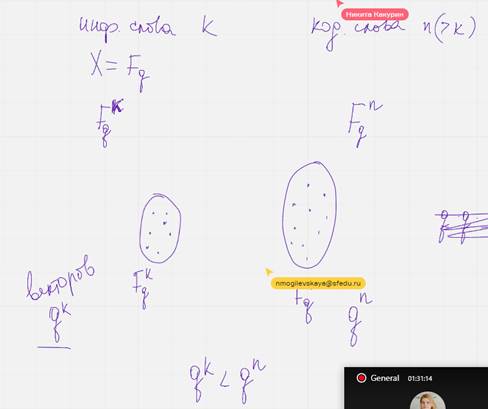

Кодовые куда ведут стрелочки – ост не кодовое но помогающее исправить ошибки
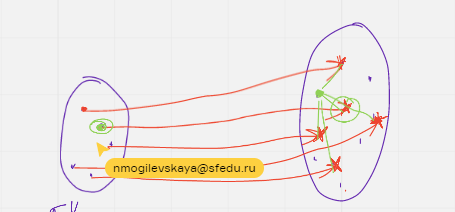
Смотрим к какому ближе свободное и декодировали
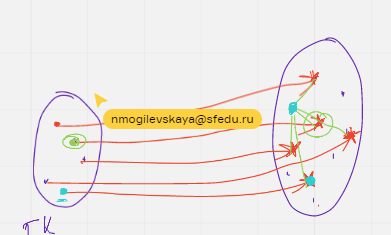
Помехоустойчивый кодер декодер (канала)
(Вспоминаем прошлую пару)

Если основание логарифма 2 – меряем кол во информации в битах
Если осн 3 то будем мерить в тритах (?)
Если 10 то диты (хартли?)

Два события х1 и х2 х3
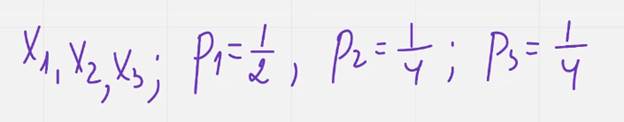

2 бита это просто кол-во (это не ее важность)
Ты сыр любишь?  (1 бит)
(1 бит) 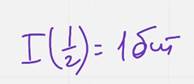
Ты меня любишь?  (Второй вопрос важнее, но получено одинаковое кол во информации) (ценность не учитывается)
(Второй вопрос важнее, но получено одинаковое кол во информации) (ценность не учитывается)
Энтропия – показывает неопределенность информации т.е насколько сложно угадать результат наступления какого либо события
Энтропия простейшего источника без памяти х с алфавитом х1 х2 итд хn и соотв вероятностями р1…рn определяется формулой

(Основание логарифма влияет ан но – биты диты итп )
Аксиоматическое определение энтропии: (аксиомы фаддеева хинчин)
1.  Не нулевая непрерывная функция вероятностей
Не нулевая непрерывная функция вероятностей  при этом
при этом 
2. Энтропия от вероятности 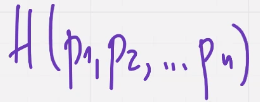 это функция симметрическая по переменным
это функция симметрическая по переменным  (симметр это такая
(симметр это такая  )
)
3. 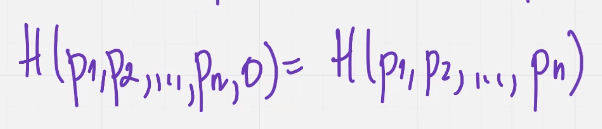
4.  (меньше чем энтропия от равных вероятностей)
(меньше чем энтропия от равных вероятностей)
 (сверху энтропию сложнее указать чем снизу)
(сверху энтропию сложнее указать чем снизу)
Называют максимальная емкость источника 
5. При n>=2

Можно сформулировать: способ выбора событий не изменяет энтропию

23.09.20
Повторяем что было
Блоковое кодирование
1 – линейность
2 – q ичность (мощность алфавита кю)
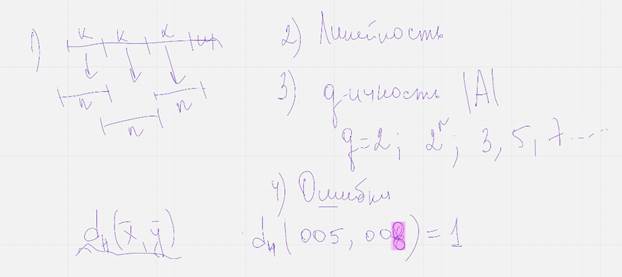
(1 – кол во не совпадающих символов)
Опр. Кодом длинны н над полем фкю называют произвольное подмножество векторного пространства фкюн 
Опр Линейным блочном кодом длины н над полем фкю называют линейное подпространство простанство фкюн далее как правило будем рассматривать линейные коды и называть их просто кодами. В случае рассмотрения не линейных кодов будем уточнять это отдельно
Отображение в поле (маленькое в большое) 
Пусть ц вложеное в фкюн произвольный линейный код длины м над полем фкю размерность которого равна к (к <=н) тогда этот код является образом некоторого линейного оператора 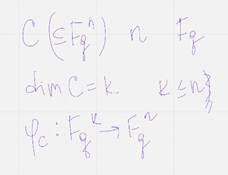
Действие оператора фиц можно выразить с помощью умножения на матрицу этого оператора (Г)
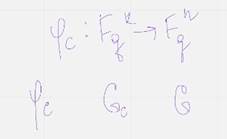
Тогда кодирование может быть выражено формулой 
Все целиком - 

Из теоремы о матрице линейного оператора вытекает что последовательность строк порождающ матрицу ж представляет собой последовательность закодированых базисных сообщений е1 е2 ек 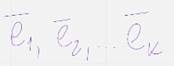 т.е в порождающей матрице записаны базисные вектора пространства (подпространства?) фкюн
т.е в порождающей матрице записаны базисные вектора пространства (подпространства?) фкюн

Как записать код 
К – размерность кода
Н – длина кода
Кю – мощность алфавита над которым построен код
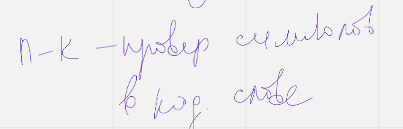 сколько проверочных символов в кодовом слове
сколько проверочных символов в кодовом слове
Будем пользоваться  скорость кода, она <1, но будем считать что <= (Для док ва теоремы доведем до абсурда)
скорость кода, она <1, но будем считать что <= (Для док ва теоремы доведем до абсурда)
Относительная избыточность – кол-во проверочных символов к длине кода 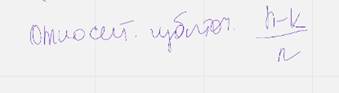
Одному коду может соотв несколько порождающих матриц  (же и же штрих)
(же и же штрих)
Опр – будем говорить, что порождающая матрица же нккю кода цэ является систематической если ее первые к столбцов представляют собой единичную матрицу  если в матрице ж можно выделить к столбцов которые составляют единичную подматрицу то порождающая матрица ж называется псевдосистематической
если в матрице ж можно выделить к столбцов которые составляют единичную подматрицу то порождающая матрица ж называется псевдосистематической
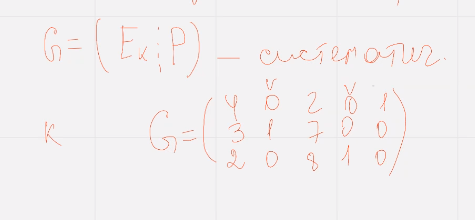
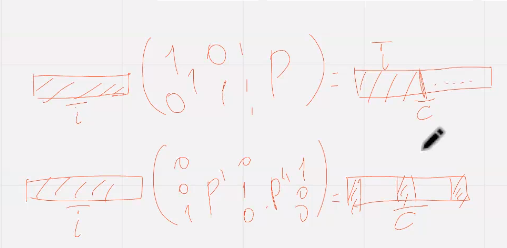
С1 – код н кратного повторения
С2 – код проверки на четность
Пример. 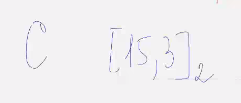 код пятикратного повторения
код пятикратного повторения

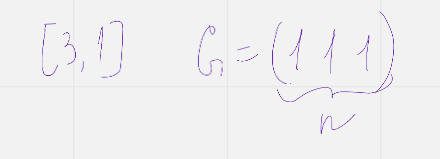 (например)
(например)
Построим мпатрицу



При передаче возникли ошибки
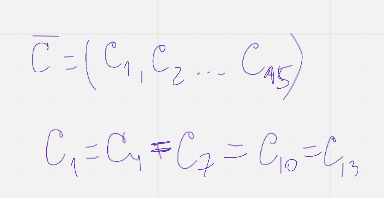
Смотрим где оно нарушается 
Мажоритарный алгоритм – решаем голосованием

Код проверки на четность

Пример 
Определение Два кода, Нккю код с1 и нккю с2 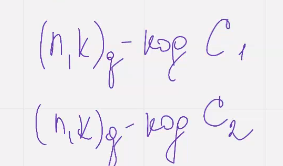 соотв порождающими матрицами г1 г2
соотв порождающими матрицами г1 г2 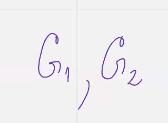 будем называть эквивалентными
будем называть эквивалентными
Если одну из порождающих матриц можно получить из другой с помощью последовательности элементарных преобразований строк и перестановкой столбцов В этом случае матрицы г1 г2 так же называются эквивалентными

Доказать что любая порождающая матрица линейного блочного кода эквивалентна систематической матрице (быстро на паре устно расказали 9:14)
Опр весом хменга вектора а называется число равное кол ву ненулевых координат 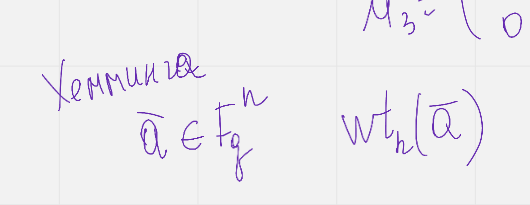 (методичка стр 87)
(методичка стр 87) 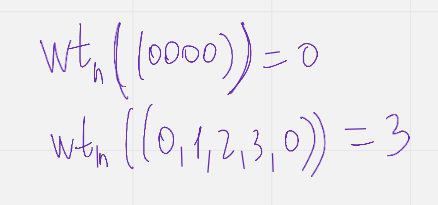
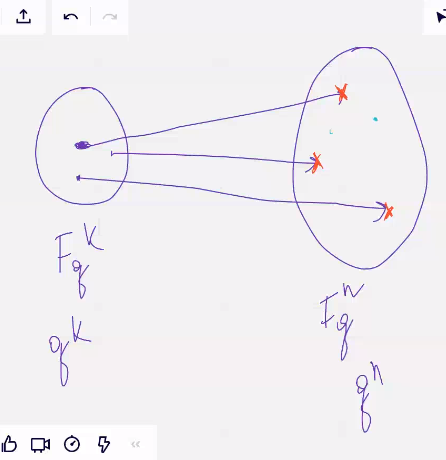
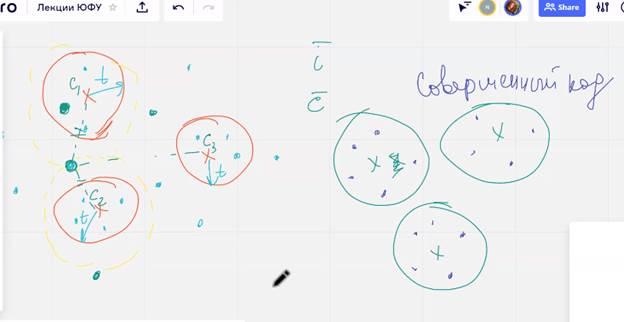 совершенный потому что нет проблем при декодировании
совершенный потому что нет проблем при декодировании
В метрическом пространстве хеминга можно обычным образом определить шары хеминга


Пример
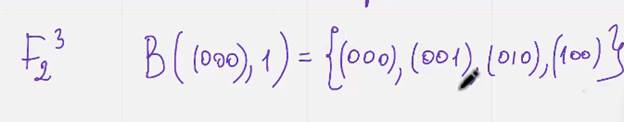
Повтор 30.09
Шар и сфера
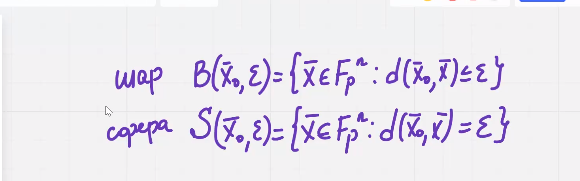
Лежит точка в шаре или нет 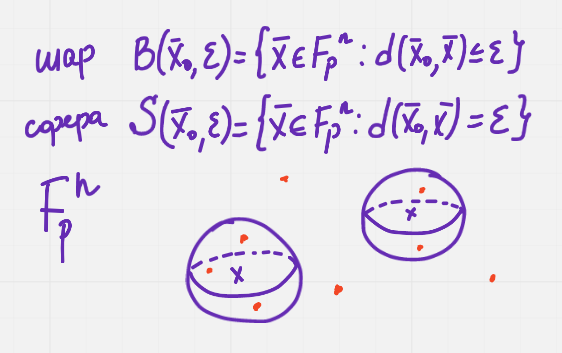
Какое кол во ошибок не портит кодовое слово 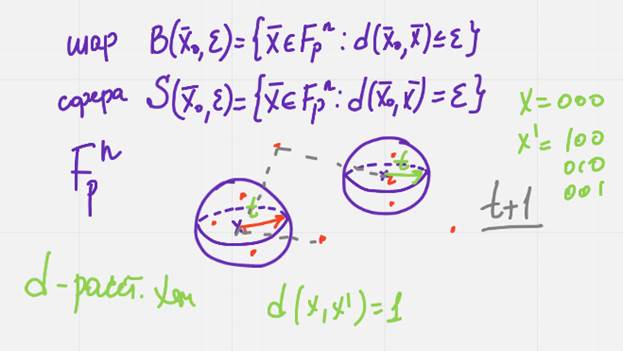
Опр Квазисовершенный код это код у которого сферы радиуса т вокруг каждого кодововго слова не пересекаются и все слова не лежащие внутри сфер лежат на расстоянии т+1 хотя бы от одного кодового слова
Опр В пространстве фкюн рассмотрим код ц, наименьшее кодовое расстояние опр формулой


Минимальное кодовое расстояние – мин значение расстояния между всеми парами кодовых слов (?)
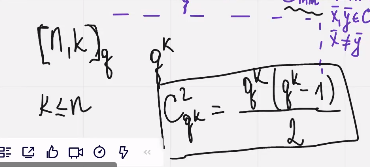
Задача нах мин код расстояния – сложная


Упрощеный способ нахождения мин кодового растояния
Лемма о вычислении мин кодового расстояния
Если ц это линейный нккю код то минимальное кодовое расстояние может быть вычислено по формуле 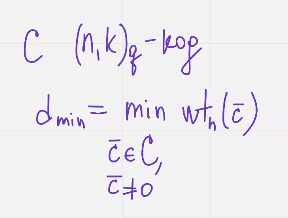


Для ненулевого кодового слова ц из кода Ц имеем. Вес Хемиинга кодового слова ц янвляется Д(ц,0) больше или равно мин кодового расстояния 
С другой стороны, если для некоторых двух различных кодовых слов у и в достигается наименьшее значение расстояния хеминга (расстояние равно д минимальному) то в силу линейности кода имеем 
Нулевое не меняем т.е в кодовом (7,4) двоичное всего 16 кодовых слов а мерять будем всего 15 (вопрос за засыпку)
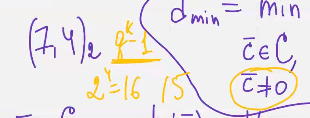
07.10
Вспоминаем - 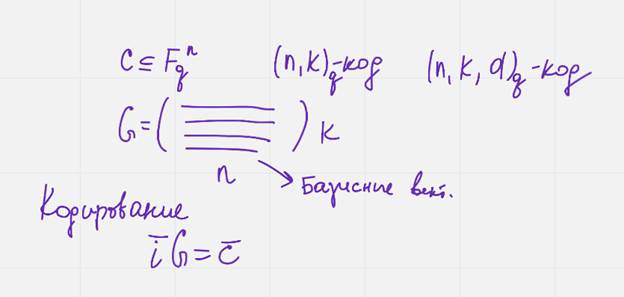
Универсальный декодер линейных блочных кодов по минимуму расстояния Хемминга (заголовок)
С точки зрения помехоустойчивости декодер является оптимальным, однако он неприемлемо затратный по времени и памяти (долгий)
1 шаг – строится таблица из двух столбцов, в одном из них находятся инф слова и , в другом – кодовые слова ц, 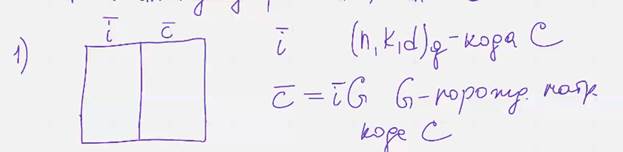
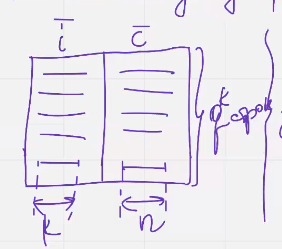
Шаг2 Пришедшая по каналу закодированная и возможно искаженное слово з  , сравнивается со всеми кодовыми словами в таблице, если з совпадает с одним из кодовых слов, то делается вывод что ошибок в з нет, а з это провильное кодовое слово
, сравнивается со всеми кодовыми словами в таблице, если з совпадает с одним из кодовых слов, то делается вывод что ошибок в з нет, а з это провильное кодовое слово
Шаг 3 – если в з есть ошибка, то в качестве правильного кодового слова, выбирается слово наиболее близкое по расстоянию хемминга ц 
Шаг 4 – по правильному кодовому слову с использованием таблицы востанавливаются соотв информационное слово и

Пример работы декодера:
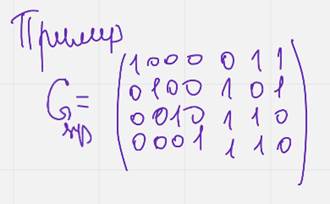 над полем
над полем 
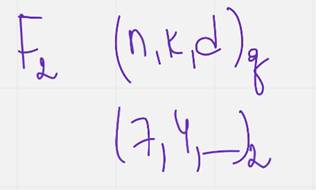

Умножаем вектор на матрицу
УПД Нашли ошибку


Узнаем мин кодовое растояние


Верное кодовое слово 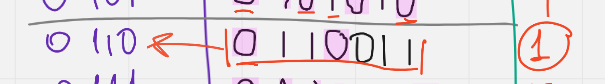


---перерыв---
Для того что бы код позволял гарантировано обнаруживать ро ошибок. Необходимо и достаточно что бы выполнялось равенство. Исправлять ку ошибок неодх достат что бы

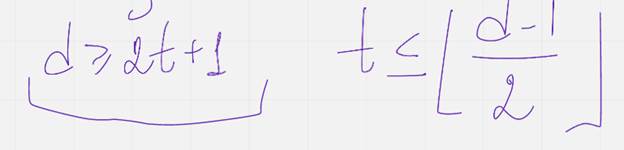 - округляем вниз 2.5 ->2
- округляем вниз 2.5 ->2
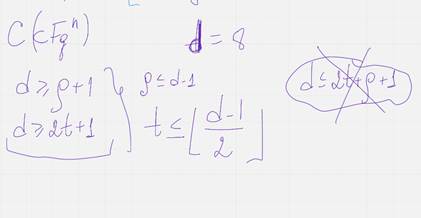
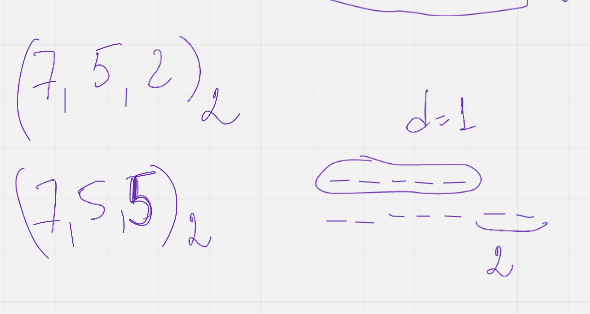
Теорема о границе синглтона

Пусть ц – произвольный нкдку код  тогда д
тогда д 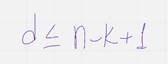
Док-во
Рассмотрим порождающую матрицу этого кода  с помощью элементарных преобразования мы можем привести ее к систематическому виду
с помощью элементарных преобразования мы можем привести ее к систематическому виду 
Код задается порождающей матрицей будет обл такими же параметрами как и исходный
Какой тут макс вес в строке? 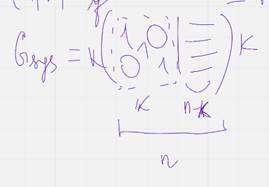
Вес каждой строки в этой матрице не превышает н-к+1 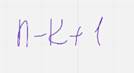
По определению д – наименьший из всех весов кодовых слов – следовательно 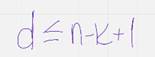
(границу доказали)
Определение:
Если для кода Ц граница синглтона выполняется как равенство, то говорят что это код с максимально достижимым расстоянием называют мдр-коды (напр относятся коды рида соломона и н-кратного повторения)

 (пример)
(пример)


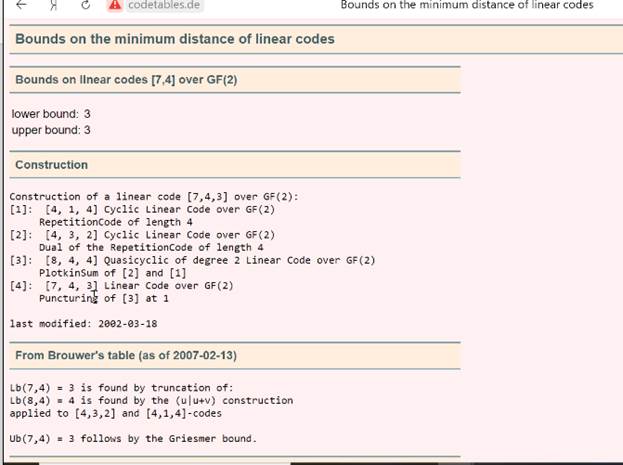
(показывают мин кодовые расстояния но и как строится такой код)
Так как код С это подпространство то для него можно построить ортогональное дополнение С-со значком 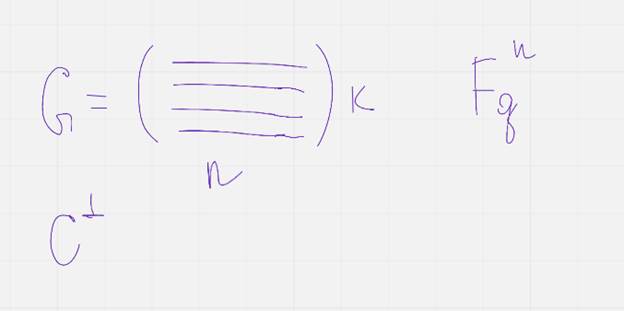
Которое так же будет являться подпространством и само может рассматриваться как код
Обозначим порождающую матрицу кода ц-з (ц со значком, как Н) 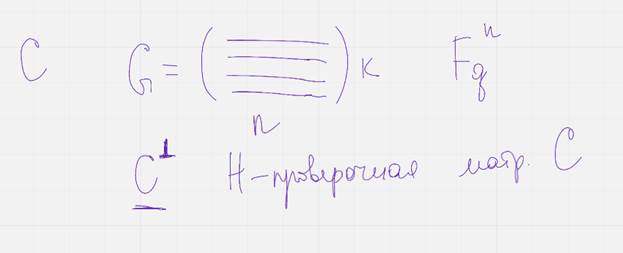
Эта матрица называется проверочной матрицей для кода ц
Очевидно, что ( порождающая матрицы связаны равенством 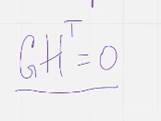
Если ж записана в систематическом виде  (единичная проверочная)
(единичная проверочная)
То соотв ей матрицу можно построить 

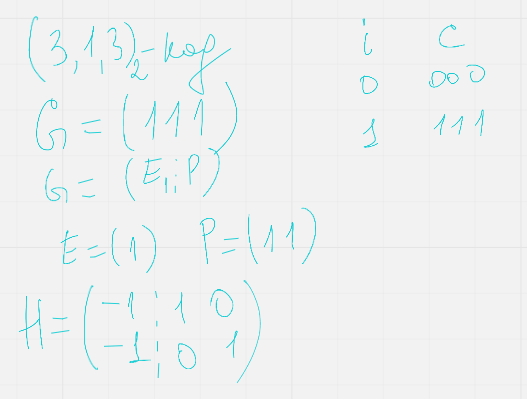 (пример)
(пример)
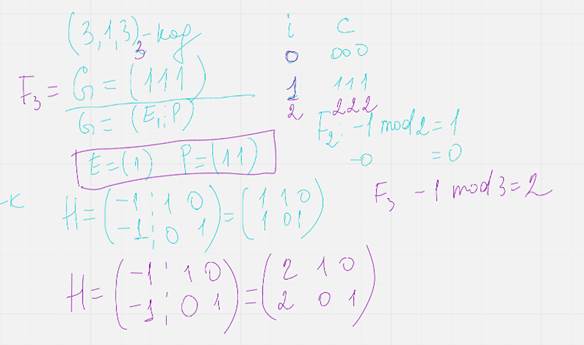

14.10.20
Вспоминаем что такое скалярное произведение


Два вектора ортогональны если их скалярное пр-е равно нулю 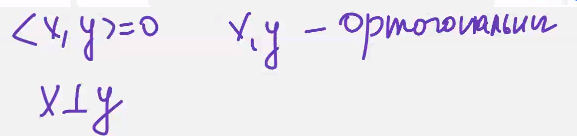
Вектора ортогональные заданому 
Для самост решения: Пусть вектора е1 е2…ек это базис пр-ва х, тогда 
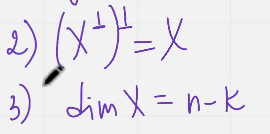

Р.м н к код ц, построим его ортогональное дополнение, параметры этого кода н-к его называют двойственным или ортогональным кодом по отношению к коду ц
Выберем в Ц ортогональный базис
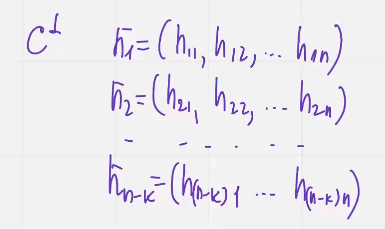 и составим матрицу из этих векторов
и составим матрицу из этих векторов
 - проверочная матрица кода ц
- проверочная матрица кода ц


Лемма Критерий кодовости слова:
Р.м нкку код ц  и его про матрицу н
и его про матрицу н  тогда
тогда

Базис ортогонального дополнения кода ц



Опр-е Р.м нкку код ц его проверочную матрицу н и какой то вектор с из фкюн 
Синдромом вектора ц называется вектор с равный

По синдрому можно проверить является ли пришедшее по каналу слово Z кодовым
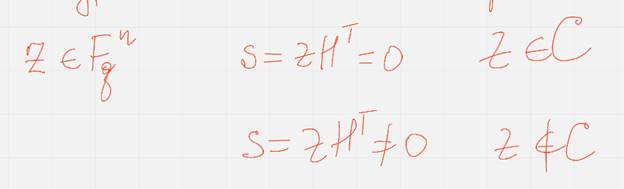
Если же синдром нулю не равен то с не кодовое
Лемма: о синдромах и ошибках
Р.м нкцу код ц и его проверочную матрицу н 
Если З пришедшее по каналу слово 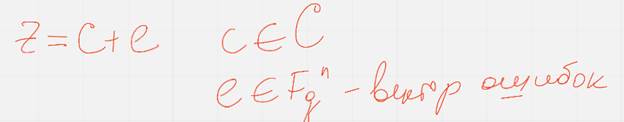
То синдром с зависит только от вектора ошибок
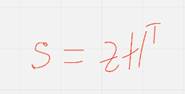
Док-во
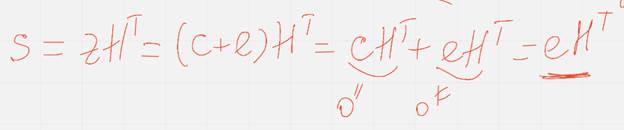
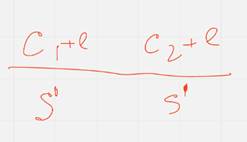
Лемма о критерии кодовости слова дает альтернативный способ задания кода, а именно как мн-во решений матричного уравнения вида  - проверочное уравнение кода ц
- проверочное уравнение кода ц
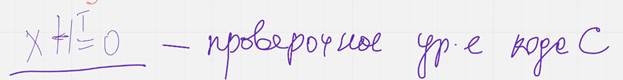
Из базиса решений этого уравнения можно сформировать кодирующую или порождающую матрицу г 
Лемма о связи между кодовой и проверочной матрицами
Р.м код нкку код ц 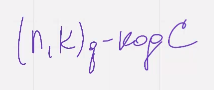 заданный с помощью порождающей и проверочной матрицы, следующее выражение справедливо (Их произведение дает ноль)
заданный с помощью порождающей и проверочной матрицы, следующее выражение справедливо (Их произведение дает ноль)

Основное ур-е помехоустойчивого кодирования 
Док-во : вытекает из леммы о критерии кодовости слова
(Строки этих матриц - базисы двух ортог пространст) 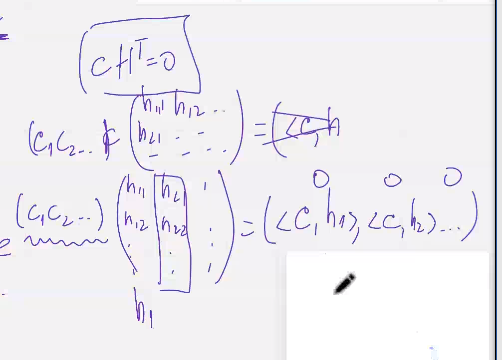
Приводим матрицу
 ( с помощью Г-сис получаем ЭКВИВАЛЕНТНЫЙ код а не тот же самый)
( с помощью Г-сис получаем ЭКВИВАЛЕНТНЫЙ код а не тот же самый)
Друг способ 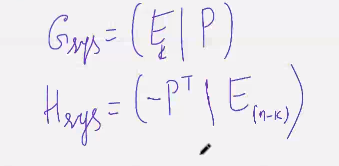
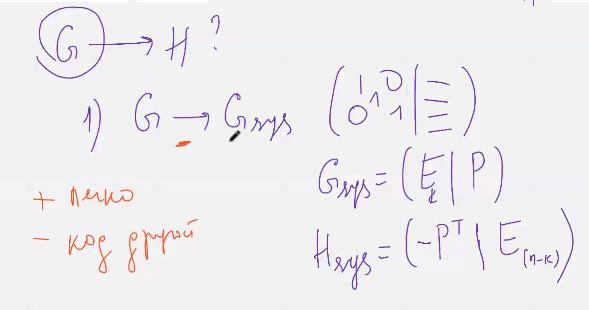
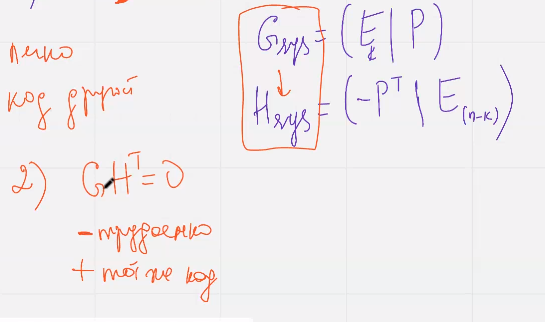
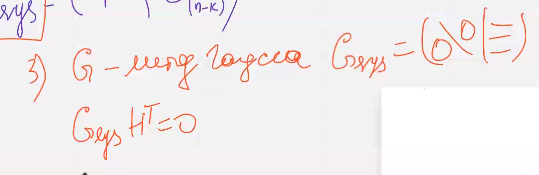 (тут нельзя переставлять столбцы, выполн только лин операции)
(тут нельзя переставлять столбцы, выполн только лин операции)

Пример:
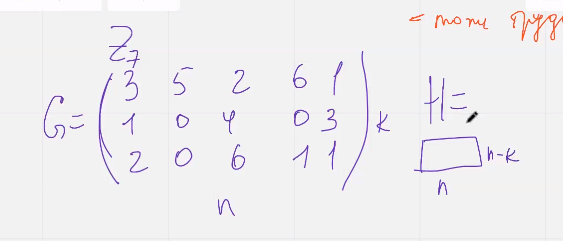
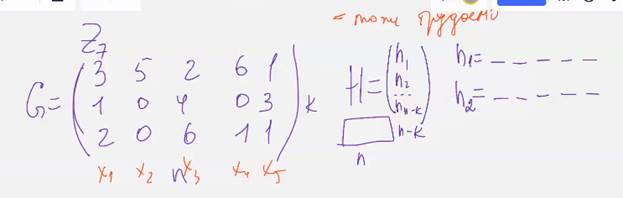
(Наш размер Н будет 5 на 2)
 обеспечили лин независимость
обеспечили лин независимость



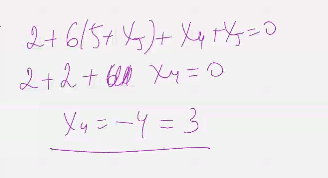 (Помним что работаем в Зед 7 т.е 7*х5 = 0)
(Помним что работаем в Зед 7 т.е 7*х5 = 0)

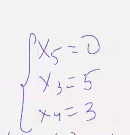
 нашли первый базисный вектор
нашли первый базисный вектор
Нет не нашли
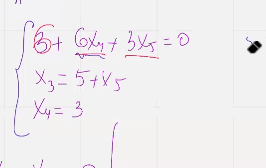
Нашли ошибку


Нашли первый, ищем второй
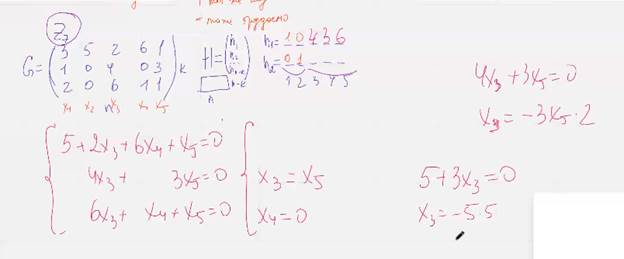
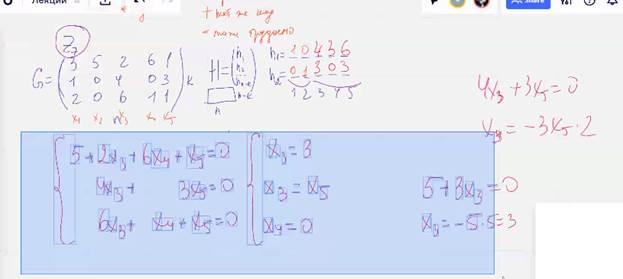



Новый пример
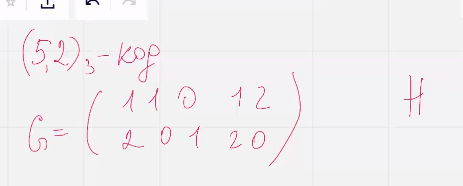
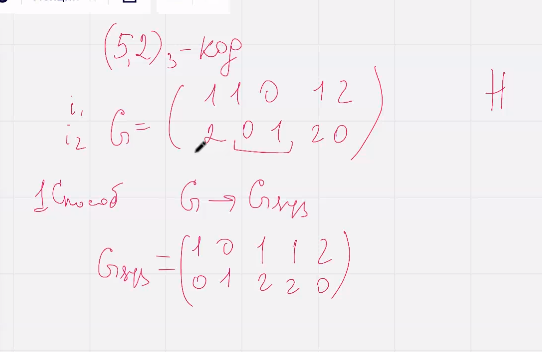


Кодировать матрицей Г-сис, декодировать матрицей Н-сис


Второй способ


21.10




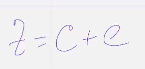
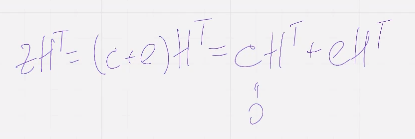 повторяем
повторяем



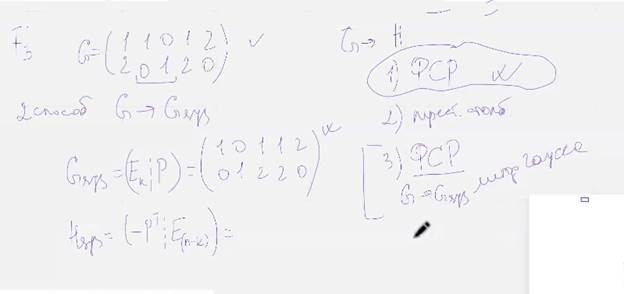
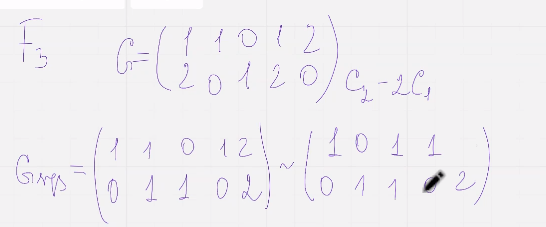

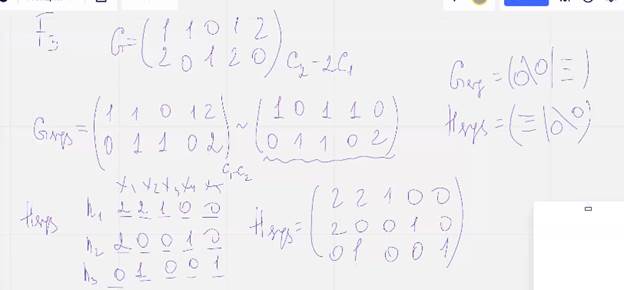
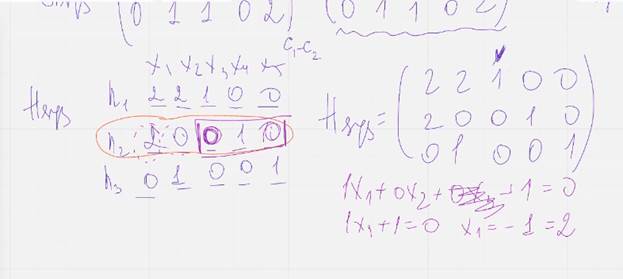
Теорема Критерий лин зависимости столбцов проверочной матрицы
Пусть бета это натуральное число  Р.м линейный код ц
Р.м линейный код ц  с проверочной матрицей Н
с проверочной матрицей Н  следующие условия эквивалентны:
следующие условия эквивалентны:
А) Существует ненулевое слово ц из Ц для которого вес хемминга не превосходит число бета 
Б) Матрица Н содержит бета линейно зависимых столбцов 

Док-во А->Б
Пусть ц такое кодовое слово что его вес  не превосходит бета,
не превосходит бета,  (
(  )множество номеров ненулевых координат вектора ц, запишем матрицу н в виде
)множество номеров ненулевых координат вектора ц, запишем матрицу н в виде 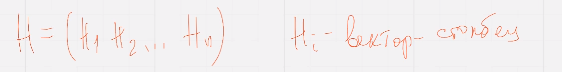 (вектор столбец), тогда
(вектор столбец), тогда  т.е
т.е 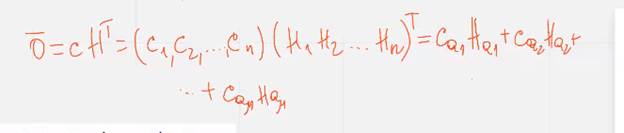
Видим что мю  столбцов матрицы н линейно зависимые , следовательно найдутся бета линейно зависимых столбцов (потому что
столбцов матрицы н линейно зависимые , следовательно найдутся бета линейно зависимых столбцов (потому что  )
)
Док во Б->А
Предположим что матрица Н содержит бета лин зависимых столбцов с номерами а1…а-бетый  тогда существуют элементы
тогда существуют элементы  не все равные нулю, такие что
не все равные нулю, такие что 
В пространстве  определим вектор
определим вектор  (определим его так что он будет явно кодовым)
(определим его так что он будет явно кодовым)
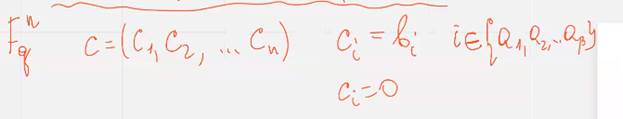
Ясно что вес вектора ц не превосходит бета 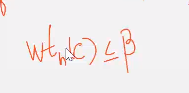 и вектор ц является кодовым т.к
и вектор ц является кодовым т.к 
Следствие 1 – пусть выполняются условия теоремы , тогда минимальное кодовое расстояние  столбцов матрицы Н линейно Независимы
столбцов матрицы Н линейно Независимы
Следствие 2 Пусть Н произвольная матрица размера n х m над полем фкю 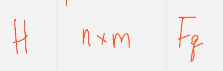 берем
берем  натуральное число, если любой набор из 2Т
натуральное число, если любой набор из 2Т  столбцов этой матрицы линейно независим, то Н это проверочная матрица -//- кода ц
столбцов этой матрицы линейно независим, то Н это проверочная матрица -//- кода ц  исправляющего т ошибок
исправляющего т ошибок 
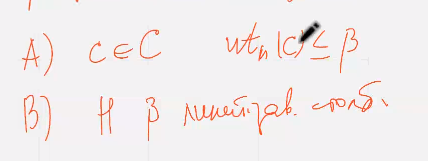 упр – доказать следствия самостоятельно
упр – доказать следствия самостоятельно

Пример: 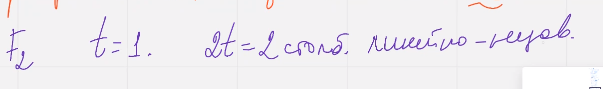
Нам достаточно построить матрицу у которой любой набор из двух столбцов был бы линейно независим. Для поля F2 это равносильно тому, что все столбцы матрицы ненулевые и различные

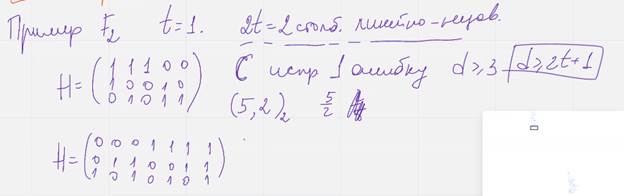
 избыточность 7/4
избыточность 7/4 
Вариант 2(где 7/4) предпочтительнее к использованию т.к меньше избыточность (он так же исправляет одну ошибку)

28.10.20
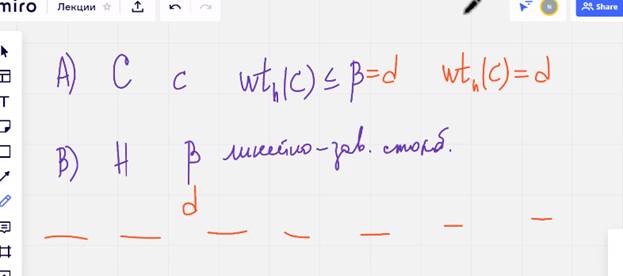 прошлая теорема в другой форме записи
прошлая теорема в другой форме записи
ТЕОР Если минимальное расстояние линейного нка кода равно д то любые л меньше либо равные д -1 столбцов матрицы н линейно независимы 
И найдутся д  линейно зависимых столбцов
линейно зависимых столбцов
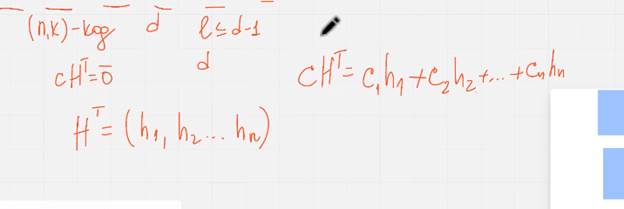
Построение линейных кодов с заданным минимальным кодовым расстоянием:
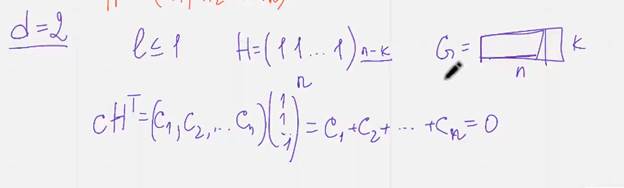


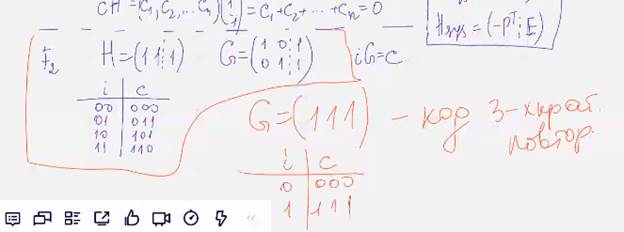
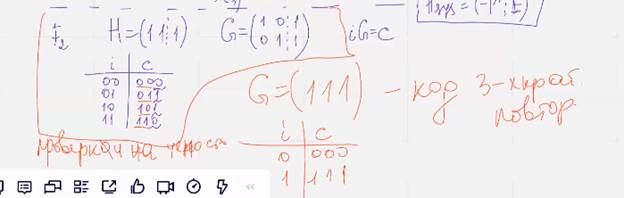
Следующий пример
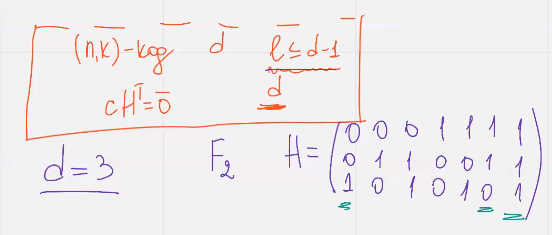
Код хемминга
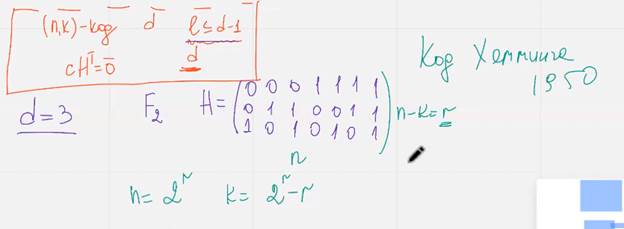

Для построения кода Хемминга нд полем фку где ку больше двух столбцами матрицы Н должны стать 
Куичные векторы длинны n которые не получаются друг из друга умножением на скаляр
Имеется ку – 1 ненулевой скаляр
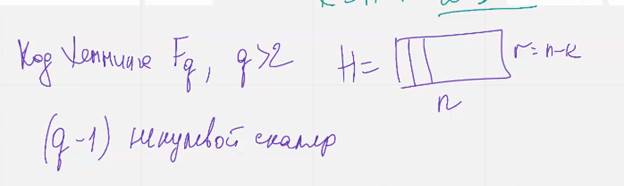

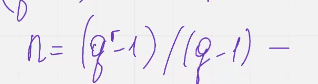 линейно независимы попарно, мин кодовое растояние 3
линейно независимы попарно, мин кодовое растояние 3 
Построим матрицу:
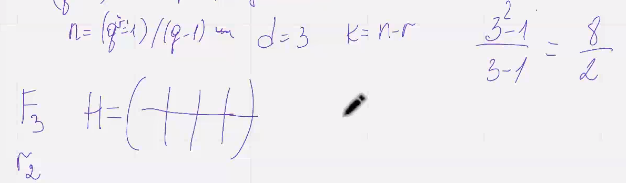

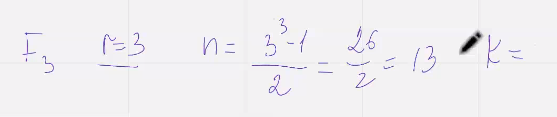
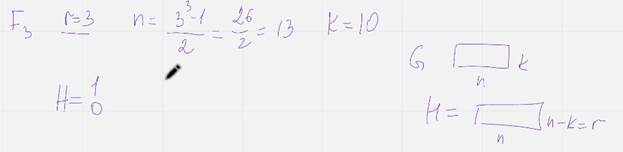
Проверочная матрица


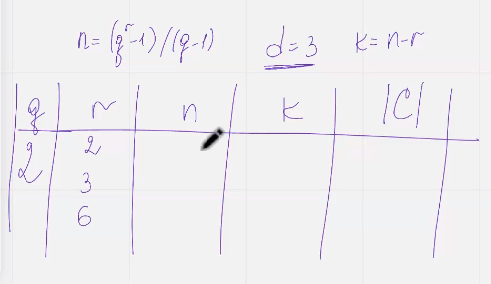
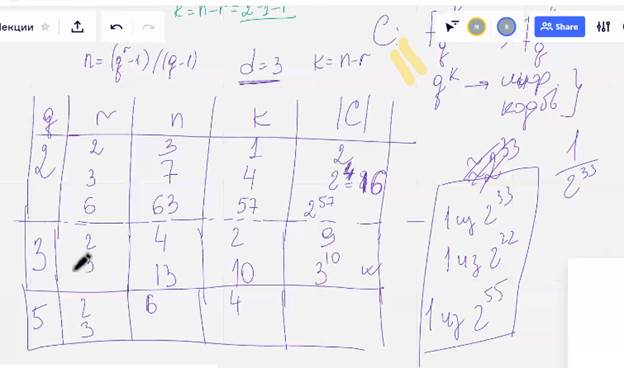
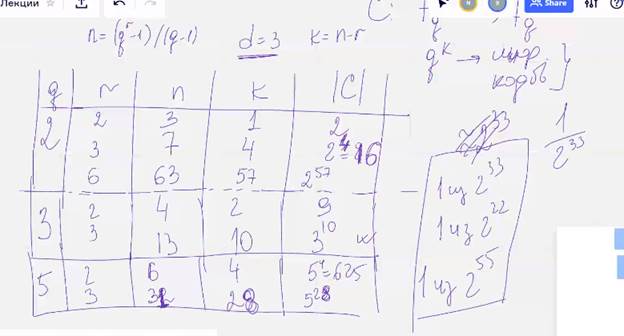
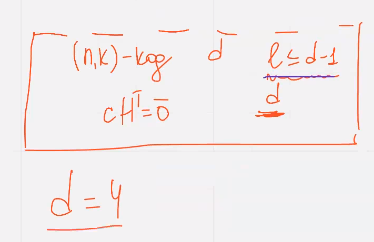

Проверочная матрица кода с D=4 любые л <=3 столбцов должны быть линейно независимыми, отсюда следует. Что при Q = 2 в матрице Н не должно быть нулевых и одинаковых столбцов 
Кроме этого, любые два столбца в сумме не должны давать третий
Проверочную матрицу, для D = 4 можно получить из Н 3 (Н у которого Д = 3) приписыванием к ней единичной строки и нулевого столбца. В этой матрице Н4 сумма двух любых столбцов не равна третьему столбцу т.к в сумме столбцов в последнем разряде будет ноль, а в матрице Н4 все столбцы в последнем разряде имеют единичку

Код построенный таким способом называется кодом расширенным проверкой на четность

Граница Хемминга
т – сколько исправляет ошибок
Пусть т это натуральное число, С – лин код фкюн, если код в С позволяет гарантировано исправить т ошибок 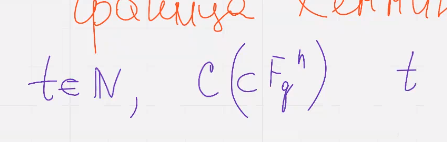 то выполняется
то выполняется 
(В разных учебниках разные формулы, если встретите другую исп преобразования)
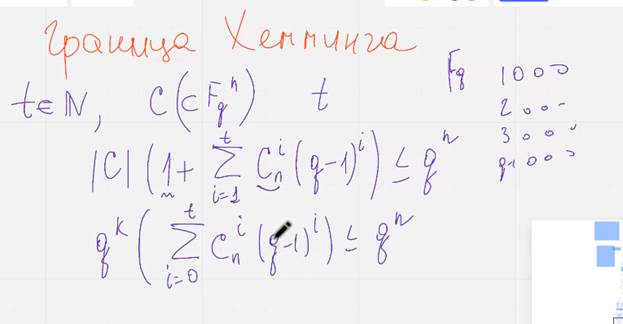
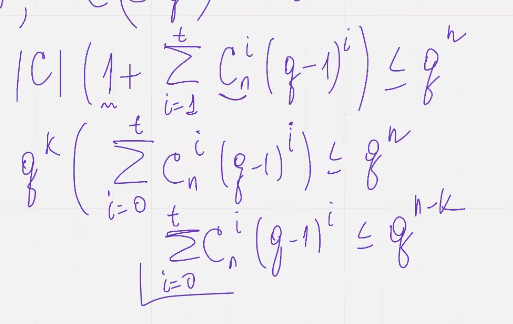
(это просто переписываем формулу в другом виде)

Если граница хеминга выполняется как равенство – код совершенный
11.11.2020
Граница синглтона 


МДР – максимально достижимое расстояние
Код хемминга не мдр 

Повторение прошлой теоремы, сколько ошибок исправляет код
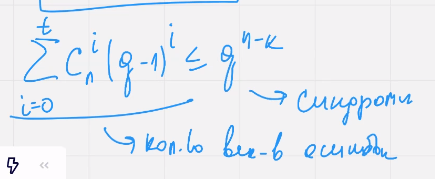 *кол во ошибок которые код может исправить
*кол во ошибок которые код может исправить


Совершенный код 
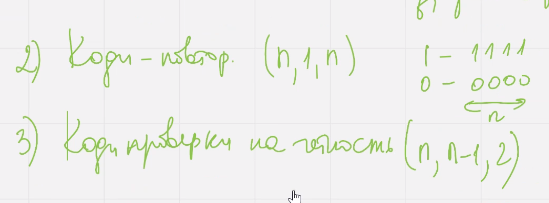

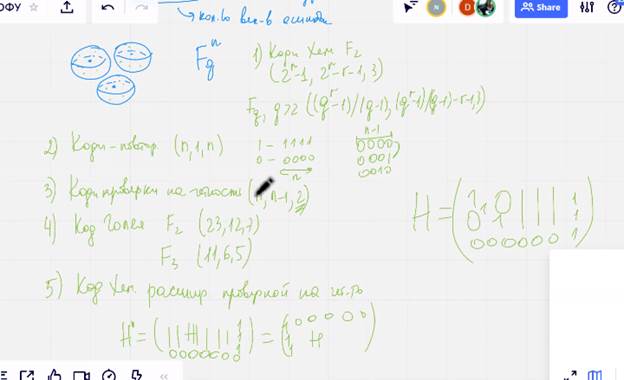
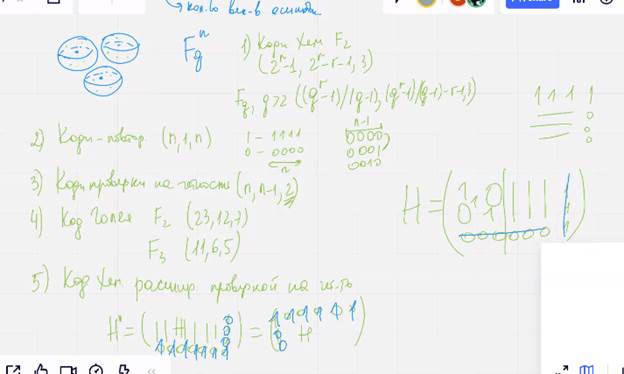
Граница гильберта
Существует нкдкю код, число слов которого удовлетворяет условию

Граница гильберта не требует от кода С линейности, аналог-я граница построена варшамовым для линейных кодов
Асимптотически эти границы совпадают и такую границу называют границой варшамова-гильберта
Теорема о границе варшамова-гильберта / нижняя граница-варшамова-гильберта
Если нкд натуральные числа, ку степень простого числа и выполняется неравенство

 то в векторном пространстве фкюн существует такой линейный код ц размерности к что его минимальное кодовое расстояние больше либо равно значению д
то в векторном пространстве фкюн существует такой линейный код ц размерности к что его минимальное кодовое расстояние больше либо равно значению д

Док во
Согласно теореме о критерии лин независимости столбцов проверочной матрицы
Для док ва теоремы о границе необходимо построить такую проверочную н-к матрицу Н над полем фку

У Которой любой набор из д-1 столбца линейно независим
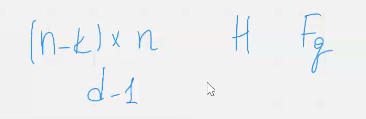
Предположим что н-к на j-1матрица кж-1 где ж-1 боллше или равно минус к уже построено

Покажем что существует такой вектор столбец что если приписать его справа матрице кжи минус один то полученное н-к на жи матрица кажи будет удовлетворять необходимому условию независимости столбов
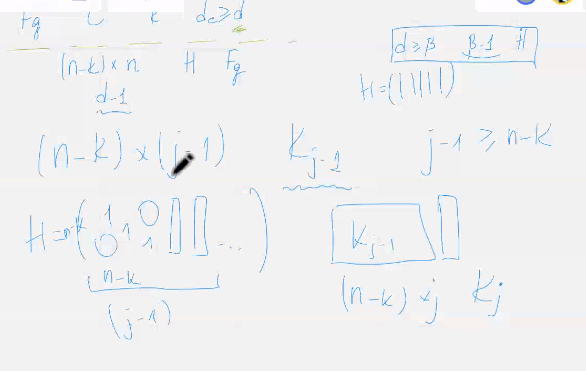
Для построения житого столбца матрица ка жи выясним сколько в пространстве фкюн минус кимеется векторов которые являются линейными комбинациями не более чем д-2 столбцов матрицы кажи минус 1
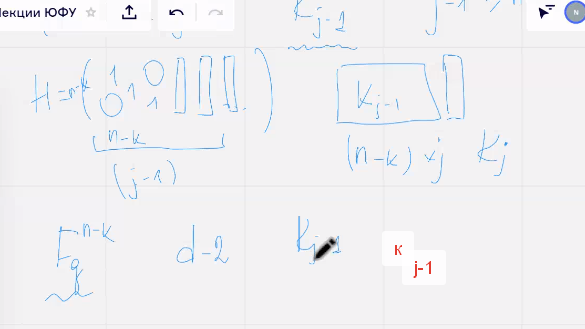
1) Нулевой вектор
2) Кол во линейных комбинаций из одного столбца без учета нулевого вектора будет

3) Кол-во линейных комбинаций из двух столбцов с ненулевыми коэфициентами равно с и жи минус один по два ку минус один в степени два
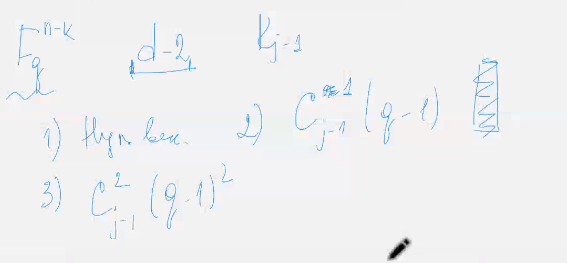
Продолжим этот процесс не учитывая не каждом последующем шаге те комбинации которые были учтены на предыдущих шагах – получим что
Кол во векторов которые являются линейными комбинациями не более чем д-2 столбцов из матрицы ка жи минус один равно

По условию теоремы выполняется неравенство * 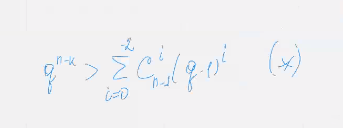
Вывод что существует по крайней мере один вектор который не является линейной комбинацией некоторого набора из д-2 векторов построенной ранее матрицы ка ж -1 
Припишем этот вектор к матрице ка жи минус один и получим
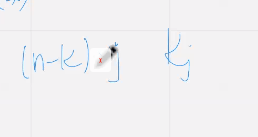
По построению матрицы любые столбцы линейно независимы (?) (помоему какие то определенные но я прослушала)

Две границы 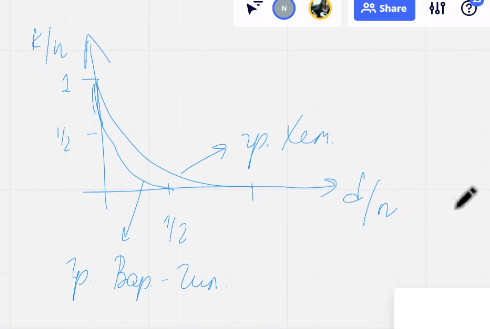
варшамова гилберта и хеминга
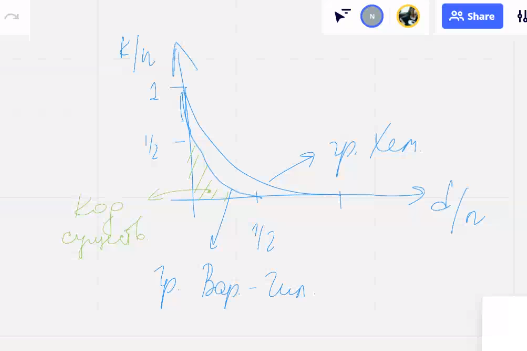

1) Если границы хеминга не выполняется то код не существует
2) Если граница варшамова гилберта выполн то код точно существует
3) Если граница варшамова гилберта не выполняется а граница хеминга выполяется (зазор между) то не понятно существует ли код с заданными параметрами
То что происходит между границами является одним из основных вопросов теории кодирования
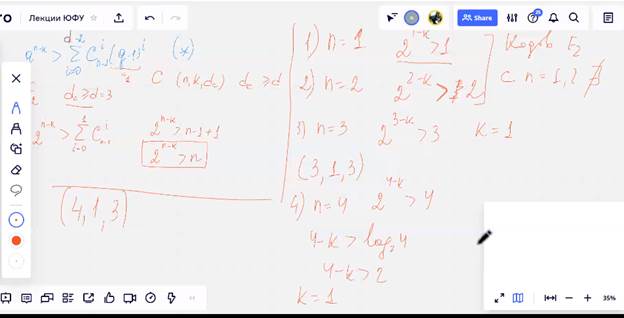
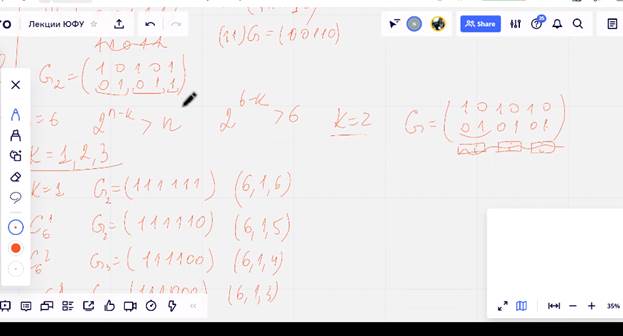
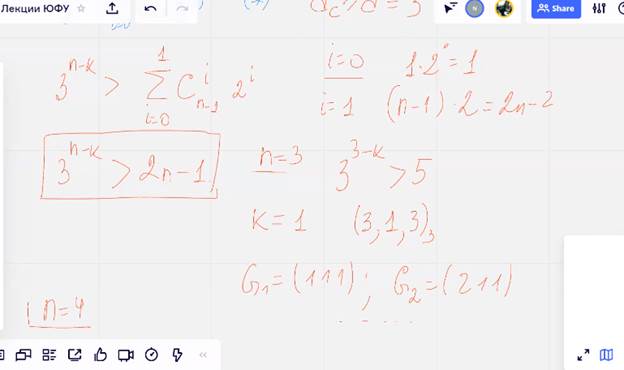
Начали строить и проверять: 


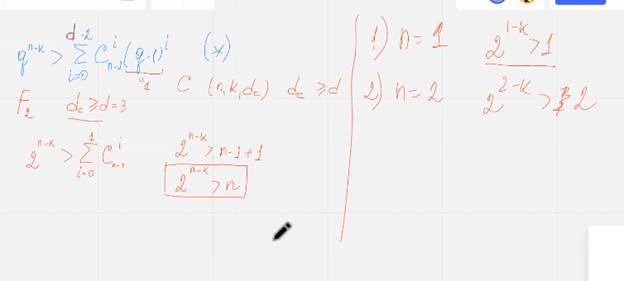 1 – решается, 2 не существует
1 – решается, 2 не существует



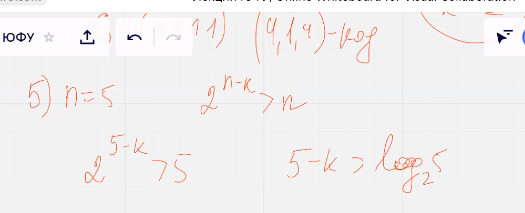







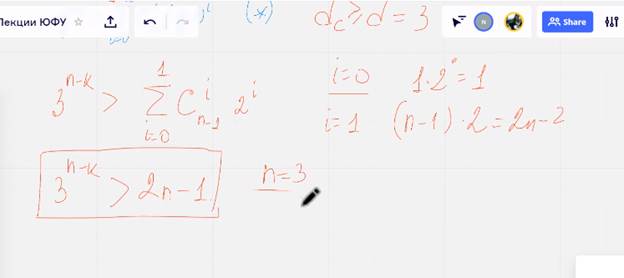
18.11.20
(Пропустила пол пары не было инета)
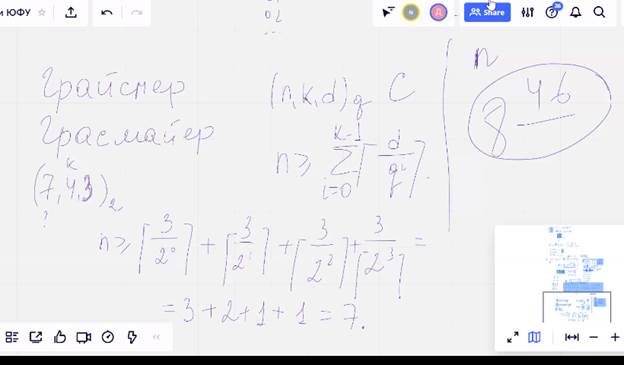
Модификации и комбинирование кодов
| Метод | Действие | Параметры кода |
| Укорочение кодов -укороченый | Удаление информационных символов | 
|
| Расширение -расширенный | Увеличение кол-ва проверочных символов | 

|
| Перфорация/выкалывание -перфорированый | Удаление проверочных символов | 

|
| Пополнение (UPD25.11) -пополненый | Добавл кодовое слово | 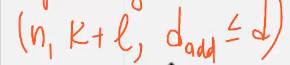
|
| Выбрасывание - код полученный с помощью модицикации выбрасывание | Удаление кодовых слов | 
|
| Удлинение кода - удлиненный | Выполняется добавление л столбцов и л строк к порождающей матрице | 
|
Укорочение кодов – пусть С линейный блочный код в параметрами нкд над полем фклю задан порождающей матрицей ж и порождающей матрицей н в систематиечском виде 
Эс – параметр укорочения 
Выбираем в диапазоне от  (строго)
(строго)
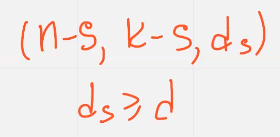
Что бы построить такой код
Порождающая матрица  можем быть получена удалением эс столбцов единичной матрицы подматрицы
можем быть получена удалением эс столбцов единичной матрицы подматрицы 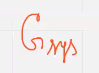 и эс строк соотв ненулевым элементам выбранных столбцов
и эс строк соотв ненулевым элементам выбранных столбцов
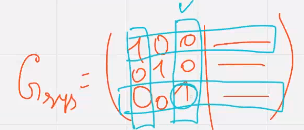
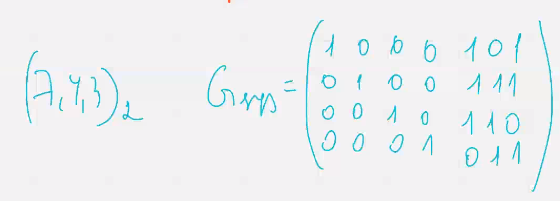
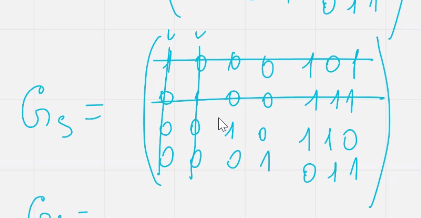


Доля проверочных символов больше чем в исходном коде
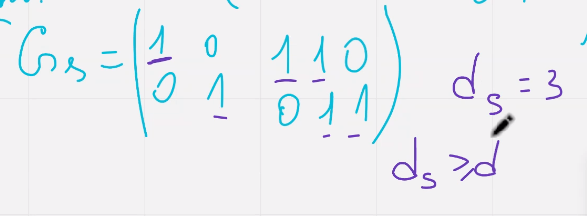
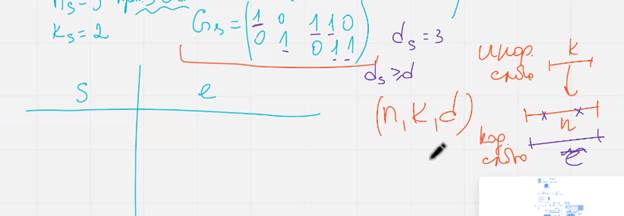
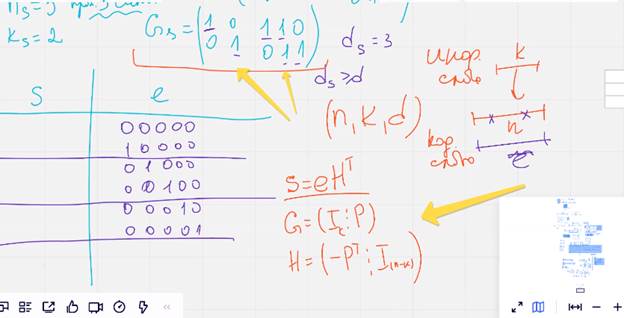

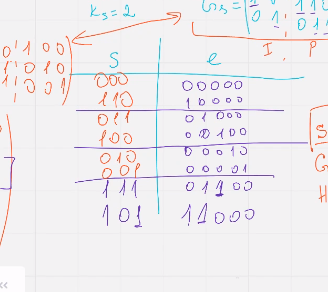
Расиширение
Расширение код ц означает добавление эпсилон проверочныз символов, 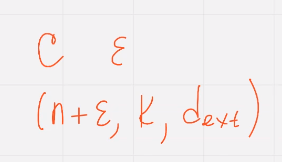
 расширенный код имеет минимальное кодовое расстояние
расширенный код имеет минимальное кодовое расстояние 
Расширенная проверочная матрица, размеры которой  получается из проверочной матрицы Н кода С с помощью добавления
получается из проверочной матрицы Н кода С с помощью добавления  эпсилон строк и столбов
эпсилон строк и столбов

Наиболее известный способ расширения состоит в добавлении общей проверки на четность
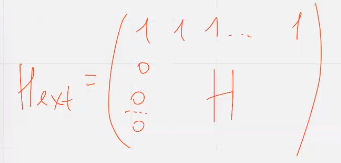
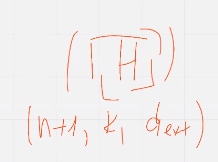
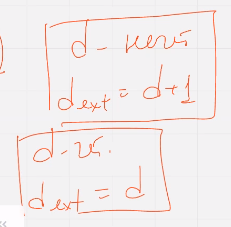 нечетный/четный случай
нечетный/четный случай
Пример:
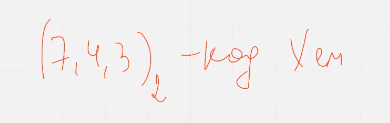
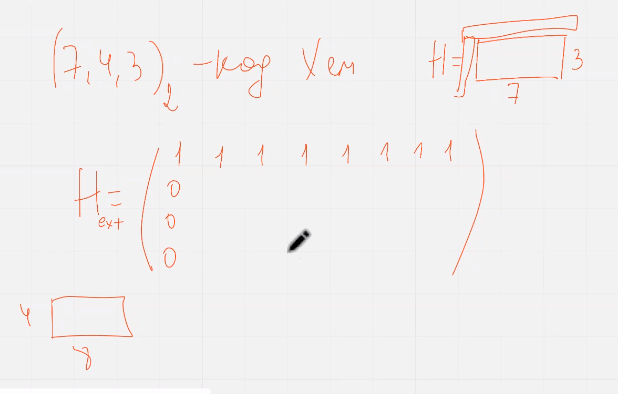

Упражнение – с помощью перестановки столбцов преобразовать матрицу, в порождающую матрицу кода рида малера с параметрами RM (1,3) (выполниться только для этих)
Перфорация приводит нас к линейному блочному коду
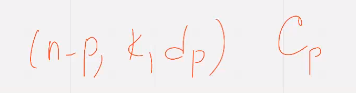
 ТАМ НЕ СТРОГО
ТАМ НЕ СТРОГО
минимальное расстояние убывает

Получаются с помощью удаления столбцов из единичной подматрицы матрицы Нсис и связанных с ними строк
Перфорация эквивалентна укорочению дуального кода


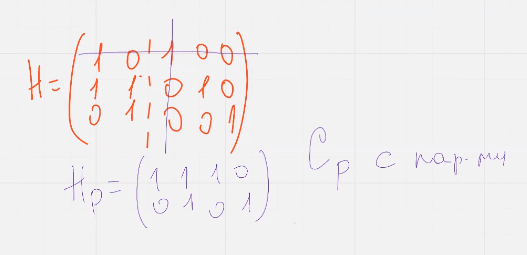
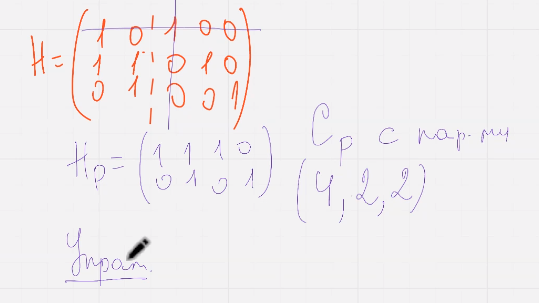 упражнение проверить что д равно 2 через теорему о лин независимости столбцов
упражнение проверить что д равно 2 через теорему о лин независимости столбцов
25.11
Вспоминаем:

Пополнение
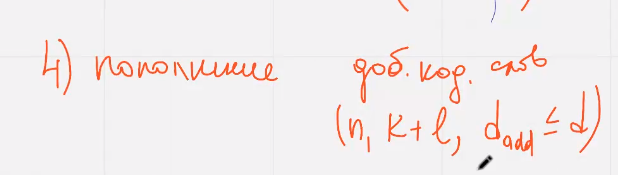
Вот тут пытались написать пример но не сохр-сь линейность 
Пополнение кода означает, добавление кодовых слов к исходному коду; для сохранения линейности удобно добавлять ЛинНезавис строки в порожд-ю матрицу
Общеизвестный способ состоит в дополнении матрицы кодовым словом из всех единиц если такое кодовое слово еще не принадлежит коду

Информационные и кодовое слова


Наша д (было 3 стало 2 (?)) уменьшилась и код перестал исправлять ошибки, зато увеличили кол-во кодовых слов
Выбрасывание – удаление кодовых слов - 
Фактически просто вычеркиваем строку
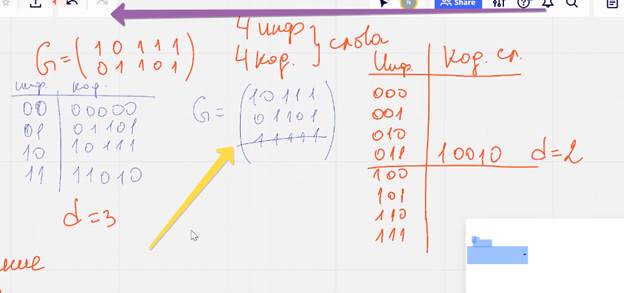
Метод: Удлинение кода
Выполняется добавление л столбцов и л строк к порождающей матрице


Зачем это все нужно (все методы):
 ->
->  ->
->  -> (30 на записи, нужно когда нужно чуть чуть подкоректировать длинну что бы не оставлять посл висящий пустой бит при передаче данных)
-> (30 на записи, нужно когда нужно чуть чуть подкоректировать длинну что бы не оставлять посл висящий пустой бит при передаче данных)
--------------Когда строим новый код в помощью комбинирования составлюящие называются компонентными
Последовательное соединение кода 
Расстроит два кода Ц1 Ц2 
Тогда последовательное соединение кодов эквивалентно поочередной передаче кодовых слов ц1 из кода Ц1 и ан но ц2
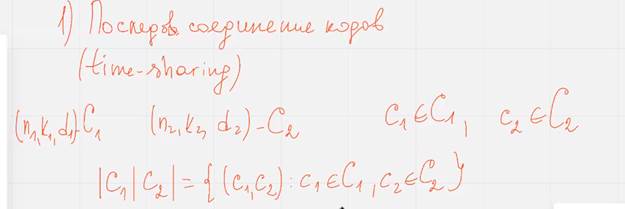
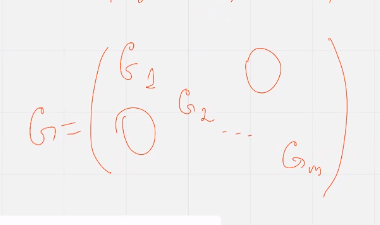
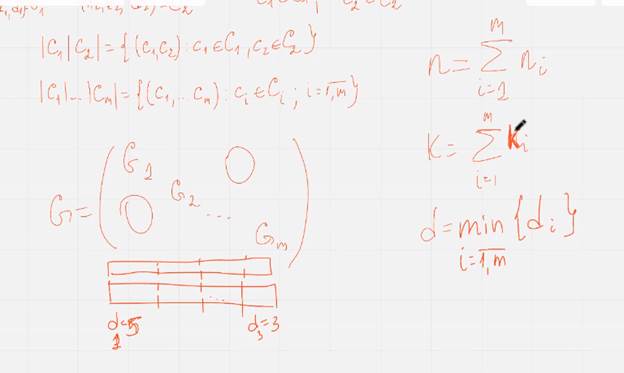
Используют в системах где нужна неравномерная система защиты от ошибок – в пакетах информация неоднородная по ценности
Последовательное соединение кодов широко используется в системах связи требующих различный уровень защиты от ошибок
Прямая сумма кодов:

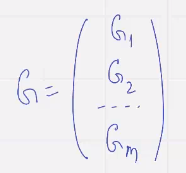
Н желательно брать фиксированным, к будет меньше или равно сумме…

Конструкция Плоткина



Коды Рида-Малера можно задать с помощью конструкции плоткина 
Тогда порожд матрица может быть построена из кода 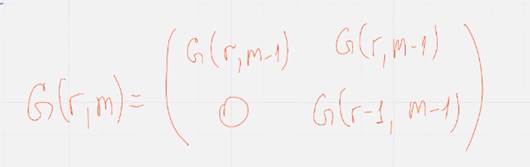
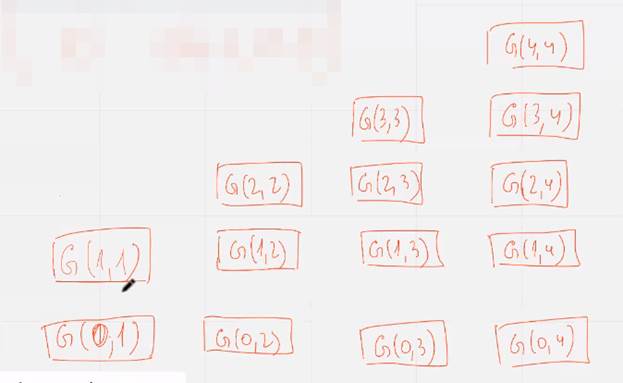

Порожд матрицу Р-м можно построить итерационно
(смотреть вот сюда) 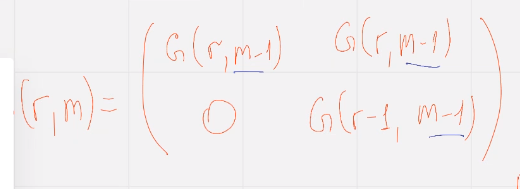
4) Конструкция Х (Маквильямс и Слоан)
5) Конструкция Х3 (икс три)
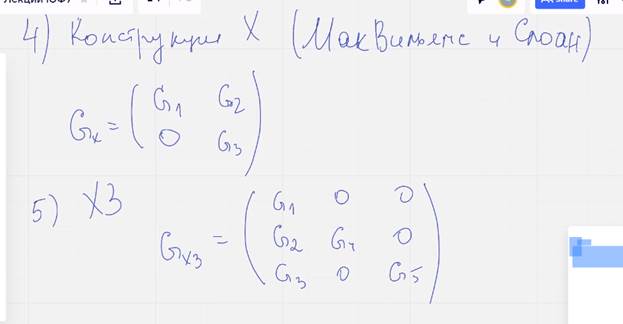
Упражнение оценить параметры кода полученного с помощью конструкции Х Х3, задуматься о роли нулей в матрицах комб кодов
6) Каскадирование кодов, автор Фарни
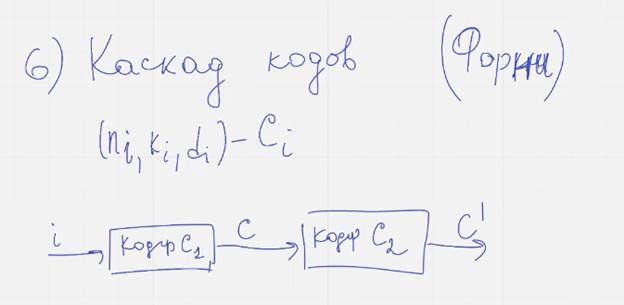
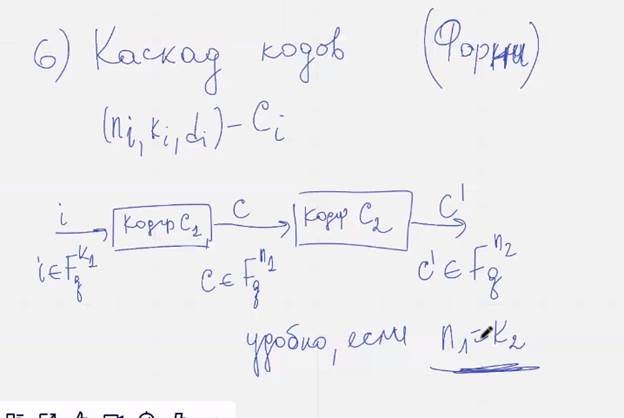
Если подчеркнутое равенство не выполнится, то 
Нужно иметь накопитель памяти

И для декодирования тоде будут нужны вспомогательные устройства
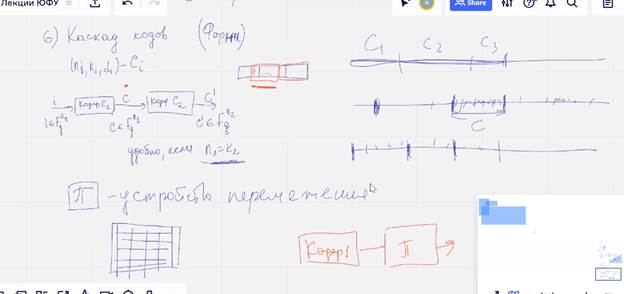
Черточки – как канал связи портит данные

Борьба с помощью каскадирования
Перемежения 
Накапливает кол во символов и передает в другом порядке  напр: записали по строчкам читаем по столбцам
напр: записали по строчкам читаем по столбцам
Наши ошибки равномерно размажет по всей длине после перемежения

7) Произведение кодов

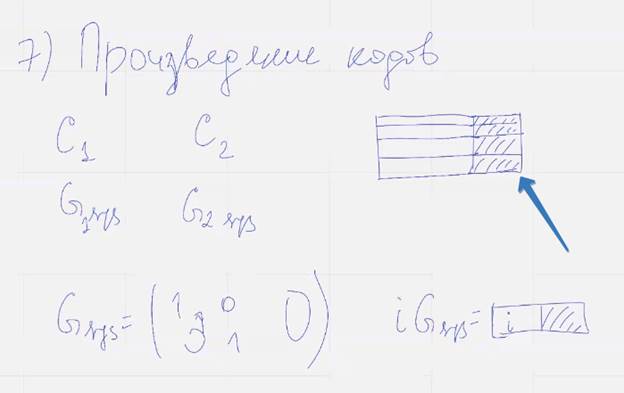
Синяя стрелка проверочные символы

Желтая стрелка – проверочные части для кода Ц2
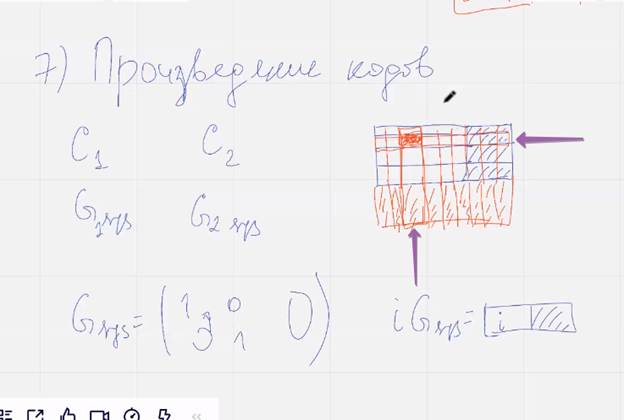 Восстановить из строки или стобца
Восстановить из строки или стобца
Проверочные двух кодов 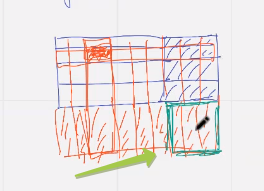
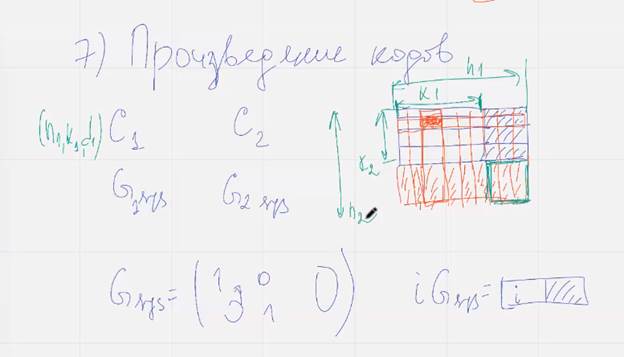

Строить такие каскады произведений кодов… в следующий раз
Дата добавления: 2021-07-19; просмотров: 88; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
