Решение двойственной задачи в среде EXCEL .
Федеральное государственное бюджетное образовательное
Учреждение высшего образования
«РОССИЙСКАЯ АКАДЕМИЯ НАРОДНОГО ХОЗЯЙСТВА
И ГОСУДАРСТВЕННОЙ СЛУЖБЫ
ПРИ ПРЕЗИДЕНТЕ РОССИЙСКОЙ ФЕДЕРАЦИИ»
СЕВЕРО-ЗАПАДНЫЙ ИНСТИТУТ УПРАВЛЕНИЯ
Факультет экономики и финансов
Кафедра бизнес-информатики
Курсовая работа на тему
«Применение математического моделирования в таможенном деле
Автор работы:
студент группы
(номер группы)
(ФИО студента)
Вариант №
Руководитель работы:
(ФИО преподавателя)
Санкт-Петербург
2021
Оглавление.
1. Задача 1. Решение транспортной задачи.
1.1. Решение «вручную».
1.2. Решение в среде EXCEL.
1.3. Решение двойственной задачи в среде EXCEL.
2. Задача 2. Обработка выборочной совокупности.
2.1. Вычисление характеристик выборки непосредственно по выборке.
2.2. Составление интервального ряда
2.3. Нахождение числовых характеристик выборки по ряду.
2.4. Построение гистограммы относительных частот и графика (гистограммы)
2.5. Проверка гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона.
Задача 3. Построение моделей системы массового обслуживания.
3.1. Многоканальная система массового обслуживания с ограниченной очередью
3.2. Многоканальная система массового обслуживания с неограниченной очередью (с ожиданием).
1.Задача 1.
Дано:
Имеется 3 склада однотипной продукции и 5 потребителей. Количество товара и цены перевозки единицы продукции даны в таблице.
| Цена перевозки единицы товара. | Запасы на складах: | |||||
| 15 | 23 | 2 | 19 | 17 | 150 | |
| 17 | 13 | 14 | 12 | 20 | 200 | |
| 13 | 21 | 24 | 16 | 12 | 100 | |
| Заявки потребителей: | 90 | 150 | 75 | 60 | 75 | 90 |
Требуется составить план перевозок таким образом, чтобы суммарная цена перевозок была бы минимальной.
1.1. Решение «вручную».
Введем обозначения:
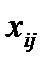 - количество товара, перевозимое от склада номер i к потребителю номер j.
- количество товара, перевозимое от склада номер i к потребителю номер j.
 - количество потребителей (заявок). В нашей задаче
- количество потребителей (заявок). В нашей задаче 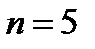 .
.
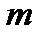 - количество поставщиков (складов). В нашей задаче
- количество поставщиков (складов). В нашей задаче 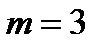 .
.
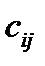 - цена перевозки единицы товара, перевозимого от склада номер i к потребителю номер j.
- цена перевозки единицы товара, перевозимого от склада номер i к потребителю номер j.
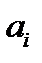 запас на складе номер i.
запас на складе номер i.  - заявка потребителя номер j.
- заявка потребителя номер j.
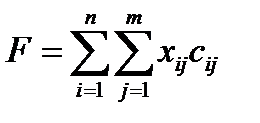 - суммарная стоимость всех перевозок. Значение
- суммарная стоимость всех перевозок. Значение  следует сделать минимальным, построив оптимальный план перевозок.
следует сделать минимальным, построив оптимальный план перевозок.
Проверим, является ли наша задача сбалансированной: 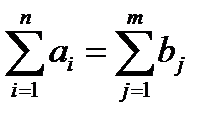 . Действительно, 150+200+100=90+150+75+60+75=450. То есть задача закрытая.
. Действительно, 150+200+100=90+150+75+60+75=450. То есть задача закрытая.
Напомним условия допустимого плана перевозок
| Количество перевозимого товара. | Запасы на складах 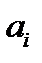 : :
| |||||
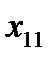
| 
| 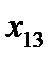
| 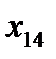
| 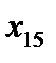
| 150 | |
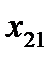
| 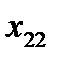
| 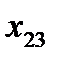
| 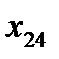
| 
| 200 | |
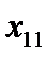
| 
| 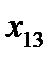
| 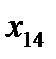
| 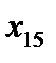
| 100 | |
Заявки потребителей  : :
| 90 | 150 | 75 | 60 | 75 | 90 |

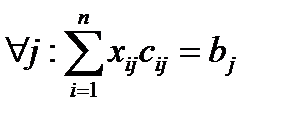 всего здесь записано m+n равенств. Также ставятся условия
всего здесь записано m+n равенств. Также ставятся условия 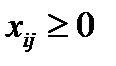 , то есть нельзя везти товар от потребителя к поставщику.
, то есть нельзя везти товар от потребителя к поставщику.
Составим первоначальный план перевозок методом северо-западного угла:
| Количество перевозимого товара. | Запасы на складах: | |||||
| 90 | 60 | 150 | ||||
| 90 | 75 | 35 | 200 | |||
| 25 | 75 | 100 | ||||
| Заявки потребителей | 90 | 150 | 75 | 60 | 75 | 90 |
Проверим этот план на не вырожденность. Количество заполненных клеток должно быть
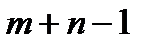 . Действительно, имеем 7 заполненных клеток, что равно 3+5-1. Наш первоначальный план не вырожденный.
. Действительно, имеем 7 заполненных клеток, что равно 3+5-1. Наш первоначальный план не вырожденный.
Далее находим пустую клетку с отрицательным ценовым балансом, и перемещаем нужное количество товара по циклу клетки. Нужное количество есть минимальное количество в отрицательных вершинах цикла. После каждого перемещения, получаем новый план, которым проделываем то же самое. До тех пор, пока в плане не будет пустых клеток с отрицательным ценовым балансом. В нашей задаче оказалось достаточно двух перемещений:

Последний план оптимальный:
| Количество перевозимого товара. | Запасы на складах: | |||||
| 75 | 75 | 150 | ||||
| 150 | 50 | 200 | ||||
| 15 | 10 | 75 | 100 | |||
| Заявки потребителей | 90 | 150 | 75 | 60 | 75 | 90 |
Суммарная цена перевозок равна  .
.
Решение в среде EXCEL.
Для решения задачи на листе EXCEL построим отдельно матрицу перевозок, вычисленную методом северо-западного угла, и матрицу цен. Просуммируем столбцы и строки матрицы перевозок и отдельно выпишем запасы на складах и заявки потребителей. Вычислим (целевая ячейка F) общую сумму перевозок. Используя последнюю, как целевую ячейку - минимум, применим ПОИСК РЕШЕНИЯ, в котором в строке ИЗМЕНЯЯ ЯЧЕЙКИ, укажем диапазон плана перевозок, а в условиях не отрицательность перевозок и необходимые равенства, написанные в предыдущем решении. После нажатия ВЫПОЛНИТЬ, получим решение: 
Результаты совпали.
Решение двойственной задачи в среде EXCEL .
Сформулируем двойственную к транспортной задачу.
Найти потенциалы 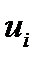
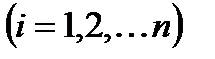 поставщиков (складов) и потенциалы потребителей
поставщиков (складов) и потенциалы потребителей 
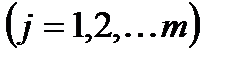 из условия максимума целевой функции
из условия максимума целевой функции  и
и 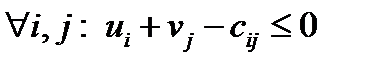 . В это й задаче у нас одна целевая функция и mn неравенств. Заметим, что здесь не требуется матрица перевозок. Но листе EXCEL запишем матрицу цен
. В это й задаче у нас одна целевая функция и mn неравенств. Заметим, что здесь не требуется матрица перевозок. Но листе EXCEL запишем матрицу цен 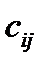 , столбец
, столбец 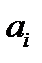 , строку
, строку 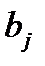 , столбец неизвестных
, столбец неизвестных 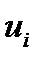 , строку неизвестных
, строку неизвестных  (пока с некоторыми произвольными значениями) и матрицу левых частей неравенств
(пока с некоторыми произвольными значениями) и матрицу левых частей неравенств 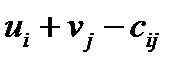 . При вычислении значений в последней матрице приходится вводить частичную защиту адресов. В ПОИСК РЕШЕНИЯ целевая ячейка – G - максимум. В ИЗМЕНЯЯ ЯЧЕЙКИ приходится ввести нерегулярный диапазон, а именно столбец
. При вычислении значений в последней матрице приходится вводить частичную защиту адресов. В ПОИСК РЕШЕНИЯ целевая ячейка – G - максимум. В ИЗМЕНЯЯ ЯЧЕЙКИ приходится ввести нерегулярный диапазон, а именно столбец 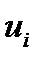 , и строку
, и строку  . В условии (одно условие) вводим неравенство для всех значений матрицы
. В условии (одно условие) вводим неравенство для всех значений матрицы 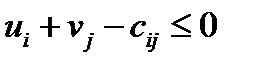 . После ВЫПОЛНИТЬ, получаем значение целевой функции G, которое равно значению целевой функции прямой задачи, а также искомые потенциалы:
. После ВЫПОЛНИТЬ, получаем значение целевой функции G, которое равно значению целевой функции прямой задачи, а также искомые потенциалы:

Задача2.
Дана статистическая совокупность Объем выборки n=120.

Проанализировать предложенную совокупность и на основе анализа
Вычислить характеристики выборки непосредственно по совокупности.
Составить интервальный вариационный ряд;
Вычислить относительные частоты;
Вычислить эмпирическую функцию распределения;
Построить графики (гистограммы) относительных частот и эмпирической функции распределения;
Вычислить выборочные: среднее значение, дисперсию, среднеквадратическое отклонение и определить выборочные моду и медиану.
Решение:
2.1 Вычисление характеристик выборки непосредственно по выборке.
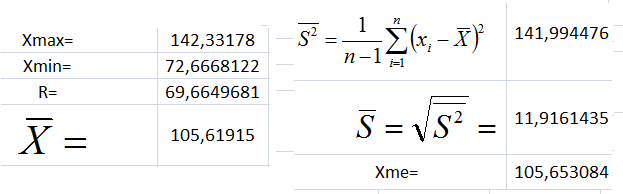
2.2 Составление интервального ряда
При n=120 формула Стерджесса (N=1+3,32lg(n), округлить до целого) дает результат: количество интервалов равно N=8. Предполагая нормальное распределение, будем находить границы интервалов из условия, что середина первого интервала равна минимальному значению, а середина последнего – максимальному. Это условие однозначно определяет все границы интервалов.
 , где R = Xmax-Xmin - размах выборки. Накопленную частоту находим через функцию ЧАСТОТА. Получаем интервальный ряд:
, где R = Xmax-Xmin - размах выборки. Накопленную частоту находим через функцию ЧАСТОТА. Получаем интервальный ряд:
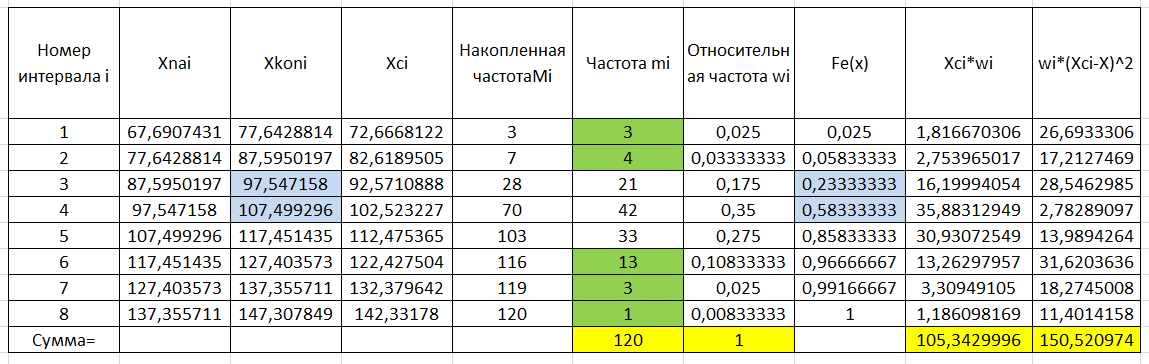
2.3. Нахождение числовых характеристик выборки по ряду.
Предположим, что сама выборка утеряна, а составленный ряд имеется. Можно приближенно вычислить числовые характеристики:
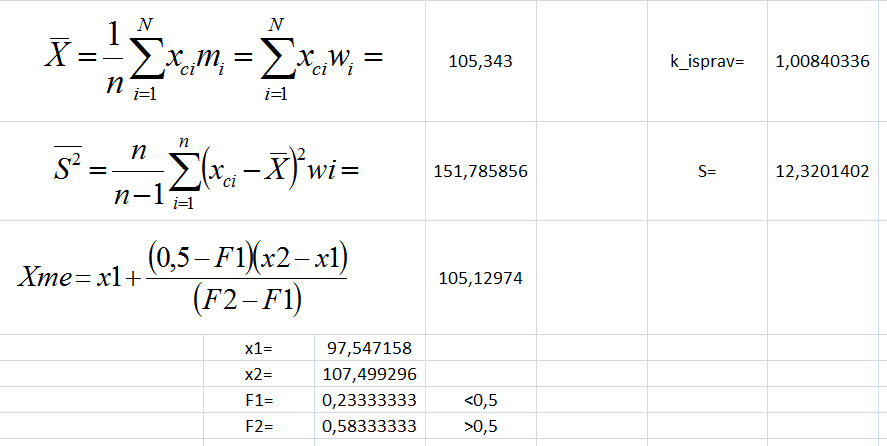
Здесь k_isprav – «исправляющий» коэффициент. При нахождении суммы 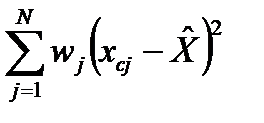 мы получаем смещенную оценку дисперсии. Несмещенная оценка получается умножением этой суммы на этот исправляющий коэффициент, равный
мы получаем смещенную оценку дисперсии. Несмещенная оценка получается умножением этой суммы на этот исправляющий коэффициент, равный  .
.
Медиана находится как значение Х, в котором функция распределения равна 0,5. Если бы значение F(x) для какого-нибудь интервала оказалось бы точно равно 0,5, то за медиану приняли бы координату конца интервала. Иначе находим соседние интервалы со значениями F(x)<0,5 и F(x)>0,5. Применяя линейную интерполяцию, находим медиану.
Видим, что значения характеристик выборки, найденные двумя способами, близкие.
2.4. Построение гистограммы относительных частот и графика (гистограммы) эмпирической функции распределения.
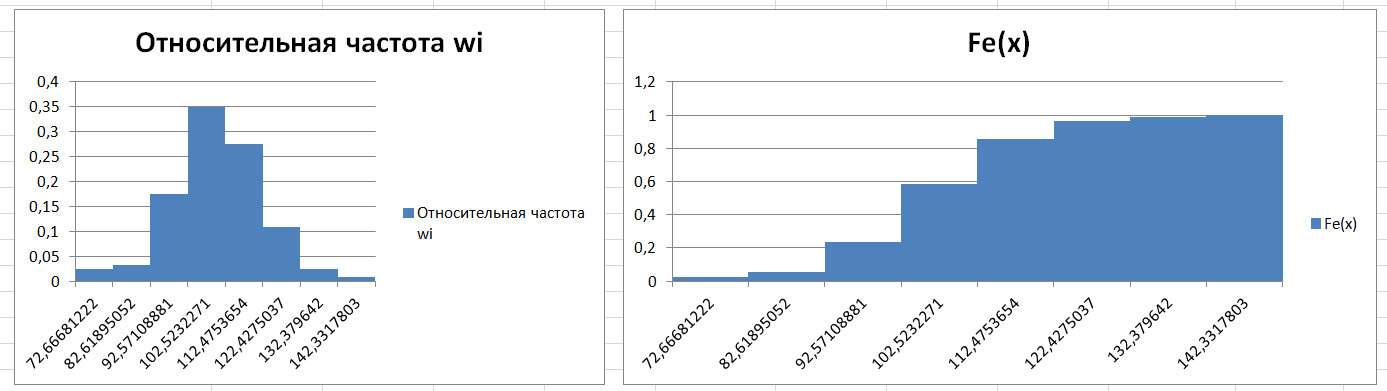
2.5. Проверка гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона.
Выдвинем гипотезу:
Н0: генеральная совокупность имеет нормальное распределение  , где
, где  105,61915 и
105,61915 и 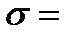 11,9161435.
11,9161435.
Н1: генеральная совокупность не распределена нормально с данными параметрами.
Уровень значимости  0,04.
0,04.
Для проверки этой гипотезы примем, что частота, равная 5 еще является репрезентативной, а меньшие значения не являются таковыми. Если есть нерепрезентативные частоты, то это заставляет объединять интервалы. В нашем случае придется объединить первый и второй интервалы, а также последние 3 интервала. В итоге получим (вместо 8) 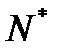 =5 интервалов. Получим такой интервальный ряд:
=5 интервалов. Получим такой интервальный ряд:
Начало первого интервала примем как -∞, а конец последнего как ∞. Для этого введем в соответствующие ячейки большие значения (-100000 и 100000). Вероятности  попадания в интервал номер i можно считать через функцию Лапласа
попадания в интервал номер i можно считать через функцию Лапласа 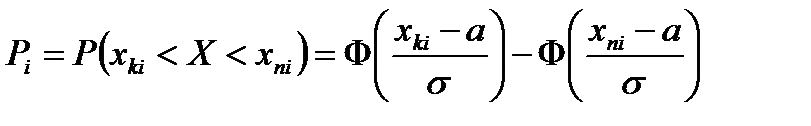 , но в EXCEL лучше считать по формуле
, но в EXCEL лучше считать по формуле 
Наблюдаемое значение H2n критерия Пирсона подсчитывается по формуле 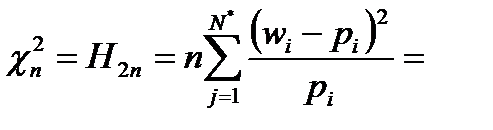 0,908. Число степеней свободы равно
0,908. Число степеней свободы равно  . Здесь
. Здесь 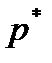 - число параметров распределения. У нормального распределения
- число параметров распределения. У нормального распределения 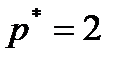 . Следовательно,
. Следовательно,  . По уровню значимости и числу степеней свободы находим критическое значение распределения хи-квадрат Пирсона (используем функцию ХИ2ОБР).
. По уровню значимости и числу степеней свободы находим критическое значение распределения хи-квадрат Пирсона (используем функцию ХИ2ОБР). 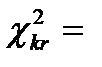 6,438. Так как
6,438. Так как  , то нулевую гипотезу принимаем.
, то нулевую гипотезу принимаем.
Задача 3
Для прохождения таможенного контроля при пересечении государственной границы к таможенному пункту с интенсивностью λ подъезжают грузовые машины. Таможенный пункт имеет n площадок для досмотра, на каждой из которых работает 1 сотрудник таможни. Время обслуживания имеет показательный закон распределения с параметром 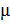 . Машины, ждущие досмотра, выстраиваются в очередь.
. Машины, ждущие досмотра, выстраиваются в очередь.
Разработать две математические модели для определения основных характеристик функционирования таможенного пункта (с ограничением по длине очереди m и с бесконечной очередью). Оценить работу пункта (многоканальной системы массового обслуживания) по следующим позициям:
1. Трафик системы
2. Показатель нагрузки на 1 сотрудника
3. Среднее число занятых сотрудников
4. Вероятность отсутствия очереди
5. Вероятность того, что придется ждать обслуживания
6. Среднее число машин в очереди
7. Среднее время ожидания в очереди
8. Среднее время обслуживания
9. Среднее число обслуживаемых машин
3.1. Рассмотрим многоканальную систему массового обслуживания с ограниченной очередью.
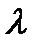 =7 интенсивность входного потока заявок.
=7 интенсивность входного потока заявок.
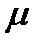 = 10 интенсивность обслуживания одного канала.
= 10 интенсивность обслуживания одного канала.
 =3 число каналов обслуживания.
=3 число каналов обслуживания.
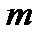 =2 число мест в очереди.
=2 число мест в очереди.
Выполним расчеты:
Коэффициент загрузки (трафик СМО) 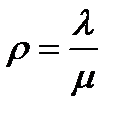 =0,7.
=0,7.
Показатель нагрузки на одного сотрудника 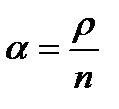 =0,2333333.
=0,2333333.
Вероятность, что в системе нет заявок 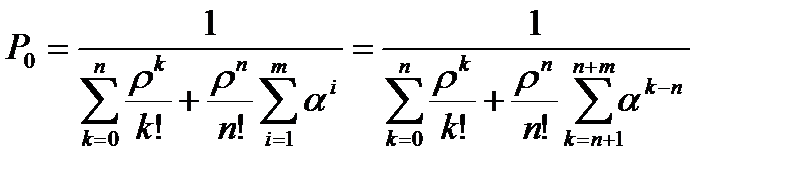 = 0,495388.
= 0,495388.
Вероятности, что в системе ровно k заявок составляют: 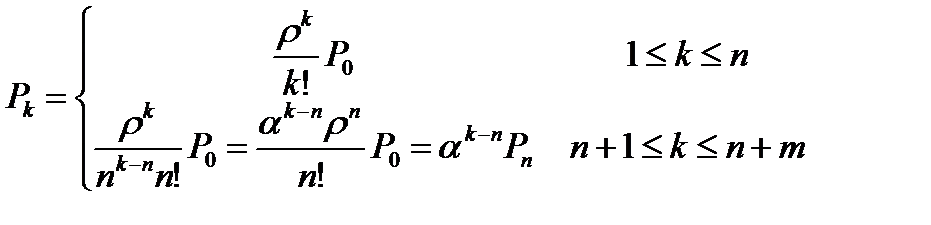
| k | Pk |
| 0 | 0,495388438 |
| 1 | 0,346771907 |
| 2 | 0,121370167 |
| 3 | 0,028319706 |
| 4 | 0,006607931 |
| 5 | 0,001541851 |
Вероятность отказа обслуживания 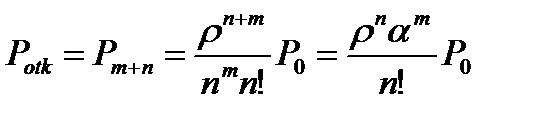 = 0,0015419.
= 0,0015419.
Относительная пропускная способность СМО 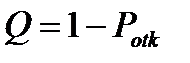 = 0,9984581
= 0,9984581
Абсолютная пропускная способность СМО 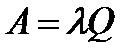 = 6,9892
= 6,9892
Среднее число занятых сотрудников (каналов) 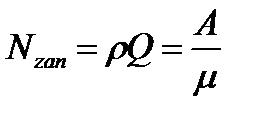 =0,69892
=0,69892
Вероятность отсутствия очереди  = 0,99185
= 0,99185
Вероятность нахождения в очереди  =0,00815
=0,00815
Среднее число машин в очереди  = 0,009691633.
= 0,009691633.
Среднее время ожидания в очереди 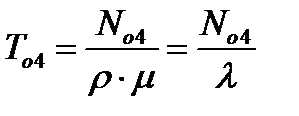 =0,0013845
=0,0013845
Среднее число машин на обслуживании 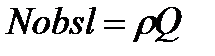 = 0,69892
= 0,69892
Среднее число машин на таможне  = 0,7086123
= 0,7086123
Среднее время пребывания на таможне 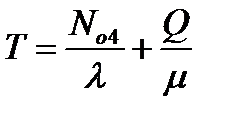 =0,10123
=0,10123
7б. Рассмотрим многоканальную систему массового обслуживания с неограниченной очередью (с ожиданием).
Исходные данные те же, что и в предыдущей модели.
Коэффициент загрузки (трафик СМО) 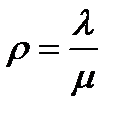 =0,7.
=0,7.
Показатель нагрузки на одного сотрудника 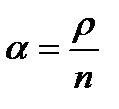 =0,223333.
=0,223333.
Вероятность, что в системе нет заявок 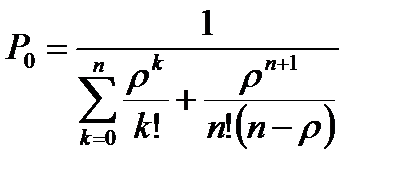 = 0,495156.
= 0,495156.
Вероятности, что в системе ровно k заявок составляют: 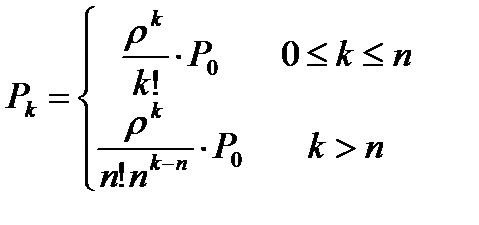
| k | Pk |
| 0 | 0,495156082 |
| 1 | 0,346609257 |
| 2 | 0,12131324 |
| 3 | 0,028306423 |
| 4 | 0,006604832 |
| 5 | 0,001541127 |
| 6 | 0,000359596 |
| 7 | 8,39058E-05 |
| 8 | 1,9578E-05 |
| 9 | 4,56821E-06 |
| 10 | 1,06591E-06 |
| 11 | 2,48713E-07 |
| 12 | 5,80331E-08 |
| 13 | 1,35411E-08 |
| 14 | 3,15958E-09 |
| 15 | 7,37236E-10 |
И т д.
Вероятность отказа обслуживания 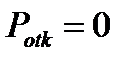
Относительная пропускная способность СМО 
Абсолютная пропускная способность СМО 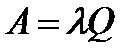 = 7
= 7
Среднее число занятых сотрудников (каналов) 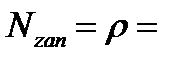 0,7
0,7
Вероятность отсутствия очереди  = 0,991385
= 0,991385
Вероятность нахождения в очереди  =0,008615
=0,008615
Среднее число машин в очереди 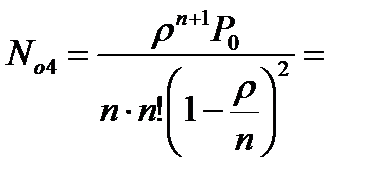 0,011236954
0,011236954
Среднее время ожидания в очереди  =0,001605279
=0,001605279
Среднее число машин на обслуживании  = 0,7
= 0,7
Среднее число машин на таможне  = 0,711236954
= 0,711236954
Среднее время пребывания на таможне 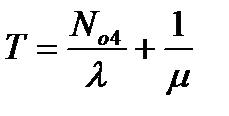 =0б101605279
=0б101605279
Заключение.
????
Дата добавления: 2021-07-19; просмотров: 525; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
