Числовые характеристики дискретных случайных величин
Элементы теории вероятностей и математической статистики
Комбинаторика изучает количество соединений, подчиненных определенным условиям, которые можно составить из элементов, безразлично какой природы, заданного конечного множества.
Произведение всех натуральных чисел от единицы до п обозначают символом п! (Читается «эн – факториал»). Используя знак факториала, можно, например, записать:
Перестановками называют соединения, состоящие из одних и тех же п различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок
,
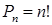где 
– факториал числа 
.
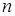Заметим, что удобно рассматривать 0!, полагая, по определению, 
.
Пример 1:Сколько трехзначных чисел можно составить из 1, 2, 3, если каждая цифра входит в изображение числа только один раз?
Решение: Искомое число трехзначных чисел
.
Размещениями называют соединения, составленные из п различных элементов по к элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений
.
Пример 2: Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2?
Решение: Искомое число сигналов
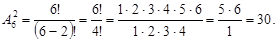
Размещения учитывают порядок следования предметов. Так, например, наборы < 2,1,3 > и < 3,2,1 > являются различными, хотя состоят из одних и тех же элементов {1,2,3}.
Сочетаниями называют соединения, составленные из п различных элементов по к элементов, которые отличаются хотя бы одним элементом. Число сочетаний
|
|
|
.
Пример 3:Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей?
Решение: Искомое число способов
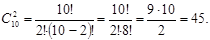
Свойства сочетаний
1. 
;
2. 
;
3. 
.
Предмет теории вероятностей.
Наблюдаемые нами события (явления) можно подразделить на следующие три вида: достоверные, невозможные и случайные.
Достоверным называют событие, которое обязательно произойдет, если будет осуществлена определённая совокупность условий S .
Пример 4: Если в сосуде содержится вода при нормальном атмосферном давлении и температуре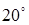 
, то событие «вода в сосуде находится в жидком состоянии» есть достоверное.
Невозможным называют событие, которое заведомо не произойдет, если будет осуществлена определённая совокупность условий S .
Пример 5: Событие «вода в сосуде находится в твердом состоянии» заведомо не произойдет, если будет осуществлена совокупность условий предыдущего примера.
Случайным называют событие, которое при осуществлении совокупности условий S может либо произойти, либо не произойти.
Пример 6:Если брошена монета, то она может упасть так, что сверху будет либо герб, либо надпись.
|
|
|
Достаточно большое число однородных случайных событий независимо от их конкретной природы подчиняется определенным закономерностям, а именно вероятностным закономерностям. Установлением этих закономерностей и занимается теория вероятностей.
Предметом теории вероятностей является изучение вероятностных закономерностей массовых однородных случайных событий.
Событие рассматривается как результат испытания.
События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.
Пример 7:Брошена монета. Появление «герба» исключает появление надписи. События «появился герб» и «появилась надпись» – несовместные.
Несколько событий образуют полную группу, если в результате испытания появилось хотя бы одно из них. Другими словами, появление хотя бы одного из событий полной группы есть достоверное событие.
Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. Итак, вероятность события А определяется формулой
.
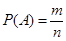Данное определение вероятности события называют классическим определением, число m называют числом благоприятных исходов, а число n – числом всех исходов.
|
|
|
Вероятность достоверного события равна единице.
.
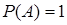Вероятность невозможного события равна нулю.
.
Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
.
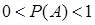Итак, вероятность любого события удовлетворяет двойному неравенству
.
Пример 8:Набирая номер телефона, абонент забыл одну цифру и выбрал ее наудачу. Найти вероятность того, что выбрана нужная цифра.
Решение: Обозначим через А событие – набрана нужная цифра. Абонент мог набрать любую из 10 цифр, поэтому общее число возможных элементарных исходов равно 10. Эти исходы несовместны, равновозможны и образуют полную группу.
Благоприятствует событию А лишь один исход (нужная цифра лишь одна). Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:
.
Относительная частота
Относительной частотой события называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний.
Таким образом, относительная частота события 
определяется формулой
|
|
|
,
где т – число появлений события, п – общее число испытаний.
Данное определение вероятности события называют статистическим определением.
Таким образом, классическую вероятность вычисляют до опыта, а статистическую (относительную частоту) – после опыта.
Пример 9:По цели произвели 24 выстрела, причем было зарегистрировано 19 попаданий. Относительная частота поражения цели
.
Операции над событиями
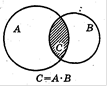
Суммой двух событий А и В называется событие С (рис. 1.), заключающееся в осуществлении во время единичного испытания или события А, или события В, или обоих событий А и В одновременно (обозначается 
или 
).
Рис. 1.
События называются противоположными, если в условиях испытания они, являясь его исходами, несовместны.
Событие, противоположное событию (то есть не наступление события ), обозначают 
. Сумма вероятностей двух противоположных событий равна единице:
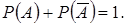
Произведением двух событий А и В называется событие С (рис. 2.), которое заключается в одновременном осуществлении обоих событий А и В во время единичного испытания (обозначается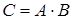 
или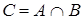 
).
Рис. 2.
Теорема сложения вероятностей несовместных событий. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
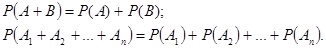
Теорема сложения вероятностей совместных событий. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
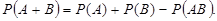
Вероятность наступления события , вычисленная в предположении, что событие 
уже произошло, называется условной вероятностью события при условии и обозначается 
.
События 
называются независимыми в совокупности, если вероятность каждого из них не меняется в связи с наступлением или не наступлением других событий по отдельности или в любой их комбинации.
Если и – независимые события, то
.
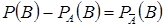Пример 10: Найти вероятность того, что наудачу взятое двузначное число окажется кратным либо 3, либо 5, либо тому и другому одновременно.
Решение: Пусть – событие, состоящее в том, что наудачу взятое число окажется кратным 3, а – в том, что оно кратно 5. Найдем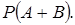 
Так как и совместные события, то воспользуемся формулой:
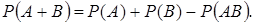
Всего имеется 90 двузначных чисел: 10, 11, …, 98, 99. Из них 30 являются кратными 3 (благоприятствуют наступлению события ); 18 – кратными 5 (благоприятствуют наступлению события ) и 6 – кратными одновременно 3 и 5 (благоприятствуют наступлению события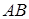 
).
Таким образом,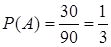 
, 
, 
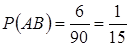, то есть
.
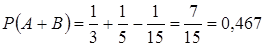Теорема умножения вероятностей независимых событий. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
.
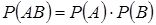Вероятность появления нескольких событий, независимых в совокупности, вычисляется по формуле
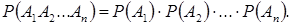
Теорема умножения вероятностей зависимых событий. Вероятность совместного появления двух зависимых событий равна произведению одного из них на условную вероятность второго:
.
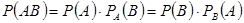Пример 11: В одной урне находятся 4 белых и 8 черных шаров, в другой – 3 белых и 9 черных. Из каждой урны вынули по шару. Найти вероятность того, что оба шара окажутся белыми.
Решение: Пусть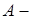 
появление белого шара из первой урны, а 
появление белого шара из второй урны. Очевидно, что события и независимы. Найдем 
, 
. Таким образом, получим
.
Формула полной вероятности
Пусть события (гипотезы) 
образуют полную группу событий и при наступлении каждого из них, например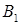 
, событие может наступить с некоторой условной вероятностью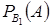 
. Тогда вероятность наступления события равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события :
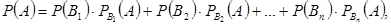
где 
Пример 12: На склад поступили детали с трех станков. На первом станке изготовлено 40 % деталей от их общего количества, на втором – 35 % и на третьем 25 %, причем на первом станке было изготовлено 90 % деталей первого сорта, на втором – 80 % и на третьем – 70 %. Какова вероятность того, что взятая наугад деталь окажется первого сорта?
Решение: Пусть 
деталь изготовлена на первом станке; 
на втором станке и 
на третьем станке; событие 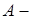деталь оказалась первого сорта. Из условия следует, что 
, 
, 
, 
, 
, 
.
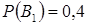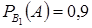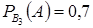Следовательно,
Формула Бернулли
Если производятся испытания, при которых вероятность появления события в каждом испытании не зависит от исходов других испытаний, то такие испытания называются независимыми относительно события .
Вероятность того, что в 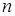независимых испытаниях, в каждом из которых вероятность появления события равна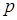 
(где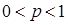 
), событие наступит ровно 
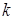раз (безразлично, в какой последовательности), находится по формуле Бернулли:
, где 
.
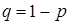Пример 13: Вероятность попадания в цель при одном выстреле составляет 
. Найти вероятность четырех попаданий при шести выстрелах.
Решение: Здесь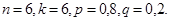 
По формуле Бернулли находим
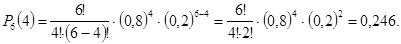
Закон больших чисел
Теорема Бернулли. Если в ряде испытаний вероятность некоторого события остается для каждого испытания постоянной и равна p,то придостаточно большом количестве испытаний практически достоверно, что частота 
появления события отличается от ее вероятности меньше, чем как угодно малое число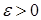 
.
Случайная величина
Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперёд не известное и зависящее от случайных причин, которые заранее не могут быть учтены.
Пример 14: Число родившихся мальчиков среди ста новорожденных есть случайная величина, которая имеет следующие возможные значения: 0, 1, 2, …, 1000.
Будем далее обозначать случайные величины прописными буквами 
, а их возможные значения – соответствующими строчными буквами 
Например, если случайная величина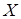 
имеет три возможных значения, то они будут обозначены так: 
Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определёнными вероятностями. Число возможных значений дискретной случайно величины может быть конечной или бесконечной.
Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений непрерывной случайной величины бесконечно.
Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями.
При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая – их вероятности:
| Х | 
| 
| … | 
|
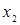
| Р | 
| 
| … | 
|
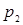
Приняв во внимание, что в одном испытании случайная величина принимает одно и только одно возможное значение, заключаем,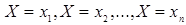 
образует полную группу; следовательно, сумма вероятностей этих событий, т.е. сумма вероятностей второй строки таблицы, равна единице:
.
Числовые характеристики дискретных случайных величин
Математическим ожиданием дискретной случайной величины называют сумму произведений всех её возможных значений на их вероятности.
Пусть случайная величина Х может принимать только значения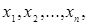 
вероятности которых соответственно равны 
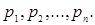Тогда математическое ожидание 
случайной величины Х определяется равенством
.
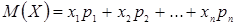Пример 15:Найти математическое ожидание случайной величины Х, зная закон её распределения:
| Х | 3 | 5 | 2 |
| p | 0,1 | 0,6 | 0,3 |
Решение. Искомое математическое ожидание равно сумме произведений всех возможных значений случайной величины на их вероятности:
.
Дата добавления: 2021-07-19; просмотров: 71; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!