Один из наиболее распространенных методов решения неравенств- метод интервалов основан на свойстве непрерывности функции.
Методические рекомендации по решению алгебраических неравенств .
Готовимся к ЕГЭ.
Учитель математики МОУ «СОШ №61»
Ленинского района г.Саратова
Вахлаева Ольга Васильевна
Содержание
Введение …………………………………………………………………………2
Глава 1 Теоретико-методические аспекты изучения темы «Алгебраические неравенства» в школьном курсе математики…………………………………..2
1.1 Анализ изложения темы «Алгебраические неравенства» в учебно-методической и научно-популярной литературе………………...…………....3
1.2 Функционально-графические методы решения неравенств………………4
1.2.1 Метод интервалов…………………………………………………….4
1.2.2 Использование свойств монотонности функций в решении неравенств………………………………………………………………………..6
1.2.3 Метод рационализации………………………………………………7
1.3 Алгебраические методы решения неравенств……...…………………….7
1.3.1 Метод равносильных переходов…………………………………… 7
1.3.2 Метод введения новых переменных………………………………...9
1.3.3 Разбиение области определения неравенства на подмножества.....9
1.4.Геометрический подход в решении неравенств…………………………...10
Глава 2 Алгебраические неравенства в контрольно-измерительных материалах государственной итоговой аттестации по математике………….11
2.1.1 Типы алгебраических неравенств, используемые на ГИА ………….....12
|
|
|
2.2.2Типичные ошибки при решении алгебраических неравенств и способы их устранения…...…………………………………………………………..…...14
Заключение .……………………………………………………………………...17
Список использованной литературы………………………………………..….28
Введение
Выпускной экзамен по математике - сложное, но необходимое испытание для всех выпускников, потому что успешная его сдача-обязательное условие для получения аттестата о среднем полном образовании, а набранные баллы по математике профильного уровня- пропускной билет в высшую школу. Поэтому выпускники серьезно и основательно готовятся к его сдаче.
В соответствии с распространенными рекомендациями все задания экзамена по математике и базового и профильного уровня условно делят на группы: самые простые, решая которые можно набрать минимальное количество баллов, перешагнуть «порог», задания среднего уровня сложности, решая которые можно набрать «хорошее» количество баллов, сложные задания, решив которые, выпускник набирает максимальное количество баллов. Задания первой группы решают все- это необходимая данность, а вот задания второй группы-для ребят знающих, творческих, амбициозных, трудолюбивых. К этой второй важной, сложной, но интересной группе заданий можно отнести и задания, связанные с решением алгебраических неравенств (задания № 18 базового уровня, задания №17 - профильного уровня). Поэтому в работе рассмотрены основные методы решения этого типа заданий.
|
|
|
Поскольку тема «алгебраические неравенства» обширна, в своей работе я остановлюсь на решении рациональных, дробно-рациональных неравенствах и неравенствах, содержащих знак модуля.
Глава 1 Теоретико-методические аспекты изучения темы «Алгебраические неравенства» в школьном курсе математики
При решении неравенств в школьном курсе используют такие основные методы: метод интервалов (обобщенный метод интервалов), метод равносильных переходов, метод введения новых переменных, метод рационализации, метод оценки и другие.
Анализ изложения темы «алгебраические неравенства» в
Учебно-методической и научно-популярной литературе
Неравенства и методы их решения включены в обязательный минимум содержания образовательных программ основного общего и среднего полного образования, поэтому эта тема изложена в школьных учебниках по математике. В УМК по алгебре для 7–9 классов Мордковича А.Г., Никольского С.М., Дорофеева В.Г., Макарычева Ю.Н., Колягина Ю. М. , а также в УМК по алгебре и началам математического анализа для 10–11 Мордковича А.Г., Никольского С.М., Дорофеева В.Г., Колягина Ю. М. . Виленкина Н.Я. и др. в полном объеме изложены основные методы решения алгебраических неравенств. В многочисленных математических справочниках, например «Повторяем и систематизируем школьный курс алгебры и начал анализа» Крамора В.С., «Математика» Гусева В.А., Мордковича А.Г. и других, эта тема также подробно изложена. В научно-популярной литературе много публикаций, связанных с нестандартными методами решения неравенств. Например, это статья Олехник, С. Н. « Уравнения и неравенства. Нестандартные методы решения. 10-11 классы» в учебно-методическом пособии, посвященном задачам, которые для школьников считаются задачами повышенной трудности или публикация «Нестандартные методы решения неравенств и их систем» Короповец З.П. Много публикаций связано с методом рационализации, его еще называют метод декомпозиции (Моденов В.П.), метод замены множителей (Голубев В.И) который получил достаточно широкое распространение, хотя в школьных учебниках он, как правило, не рассматривается. Мне показалась интересной классификация методов, представленная в работе Прокофьева А.А. и Корянова А.Г. «Решение неравенств с одной переменной». Авторы предлагают в зависимости от трактовки или интерпретации неравенства различать алгебраический, функциональный или геометрический подходы в решении неравенств. Первые два подхода различаются в понятии неравенства, которое рассматривается либо как сравнение двух выражений, либо как сравнение двух функций. При алгебраическом подходе выполняют равносильные общие (над обеими частями неравенства) или частичные преобразования неравенств (отдельных выражений, входящих в неравенство). При функциональном подходе используют свойства функций (монотонность, ограниченность и т.д.), входящих в данное неравенство. В некоторых случаях алгебраический и функциональный подходы взаимно заменяемы. Основой геометрического подхода является интерпретация неравенств и их решений на координатной прямой, координатной плоскости или в пространстве, что позволяет перейти к равносильным неравенствам, опираясь на геометрические утверждения.
|
|
|
|
|
|
1.2 Функционально-графические методы решения неравенств Функциональный подход в решении неравенств использует свойства функций.
Один из наиболее распространенных методов решения неравенств- метод интервалов основан на свойстве непрерывности функции.
Пример1(Базовый уровень)
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
Решим каждое из неравенств (предварительно приравняв левую часть к нулю) методом интервалов.
А)  ,
, 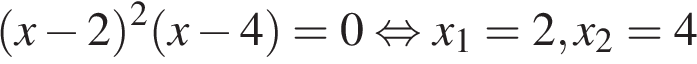
Отметим данные решения на числовой прямой и расставим знаки на соответствующих интервалах:
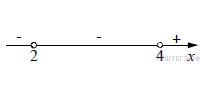 Данному решению соответствует 1)
Данному решению соответствует 1)
Б) 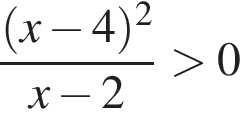 ,
, 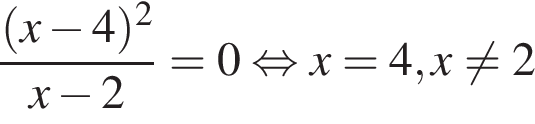
Отметим данные решения на числовой прямой и расставим знаки на соответствующих интервалах:
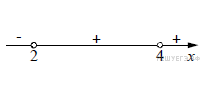 Данному решению соответствует 4)
Данному решению соответствует 4)
В) 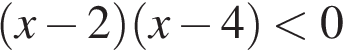 ,
, 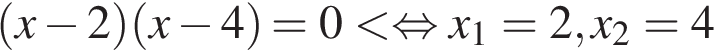
Отметим данные решения на числовой прямой и расставим знаки на соответствующих интервалах:
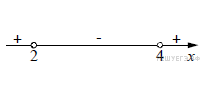 Данному решению соответствует 3)
Данному решению соответствует 3)
Г) 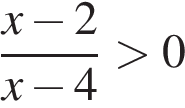 ,
, 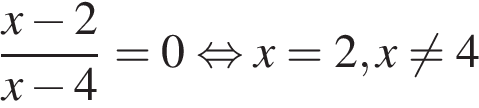
Отметим данные решения на числовой прямой и расставим знаки на соответствующих интервалах:
 Данному решению соответствует 2)
Данному решению соответствует 2)
Ответ: 1432
В рациональных неравенствах профильного уровня часто используется обобщенный метод интервалов, например, для которых при переходе из одного интервала в смежный интервал знак функции f (х) может не меняться.
Пример 2. Решите неравенство: 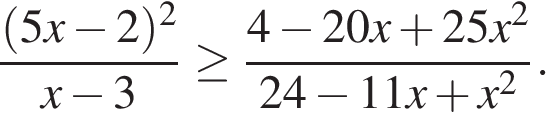
Преобразуем неравенство: 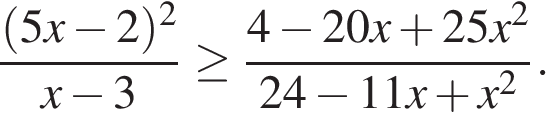

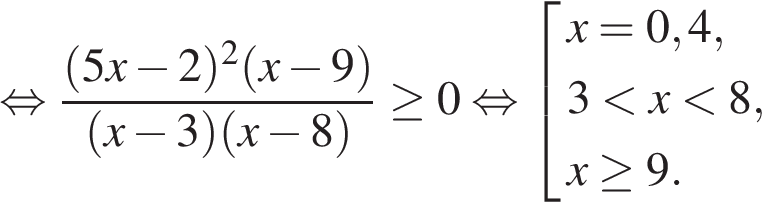
Ответ: 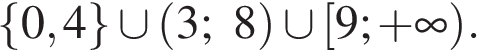
1.2.2Свойство монотонности при решении неравенств используют для случаев, когда функции, стоящие в обеих частях неравенства, имеют одинаковую монотонность или разную монотонность. Например:
Пример 3. Решите неравенство: х7+1<0.
Его можно записать его в виде х7<-17, и рассматривая функцию у= х7, которая возрастает на всей области определения, можно сделать вывод, что последнее неравенство равносильно неравенству х <-1.
Ответ: (-∞; -1).
Пример 4. Решите неравенство: (2х2+1)5 - (3х)5 >3х - 2х2-1.
Запишем неравенство как
(2х2+1)5+ 2х2+1> (3х)5+3х
Рассмотрим функцию у = t5 + t, определенную при всех действительных значениях t. Так как у ¢ (t) =5t4 +1 > 0 для любого t из области определения, то функция у(t) возрастает на всей области определения . Для возрастающей функции, определенной на всей числовой прямой, неравенство у(t1) > у(t2) равносильно неравенству t1> t2.Значит, наше неравенство равносильно неравенству 2х2+1>3х,
2х2-3х +1>0, откуда х <0,5 или х>1.
Ответ: (-∞;0,5) (1; + ∞).
1.2.3При решении неравенств методом интервалов могут возникать трудности вычислительного характера. Чтобы расширить возможности применения метода интервалов при решении неравенств, используют идею рационализации неравенств. Метод рационализации заключается в замене сложного выражения на более простое выражение, при которой более сложное неравенство равносильно более простому неравенству на области определения исходного неравенства.
Пример 5. Решите неравенство: (х2-1)2+х > (х2-1)5х-3
Запишем его как (х2-1)2+х - (х2-1)5х-3>0 и используем метод рационализации.
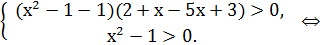
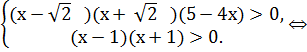
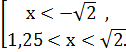
Ответ: (-¥ ; 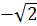 ) È (1, 25;
) È (1, 25; 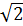 )
)
1.3 Алгебраические методы решения неравенств
1.3.1 При решении неравенств алгебраическими методами используют преобразования, позволяющие привести неравенство к более простому виду. При выполнении преобразований множество решений исходного неравенства или не меняется, или расширяется (можно получить посторонние решения), или сужается (можно потерять решения). Поэтому важно знать, какие преобразования неравенства являются равносильными и при каких условиях. Например, решая неравенство с модулем методом сведения его к равносильной системе или совокупности систем можно использовать стандартные схемы для решения, которые опираются на определение модуля, его геометрический смысл и свойства
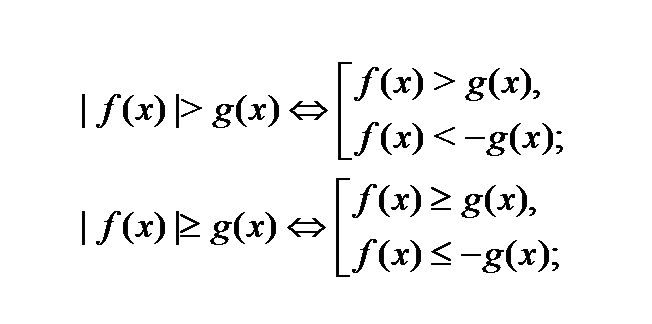
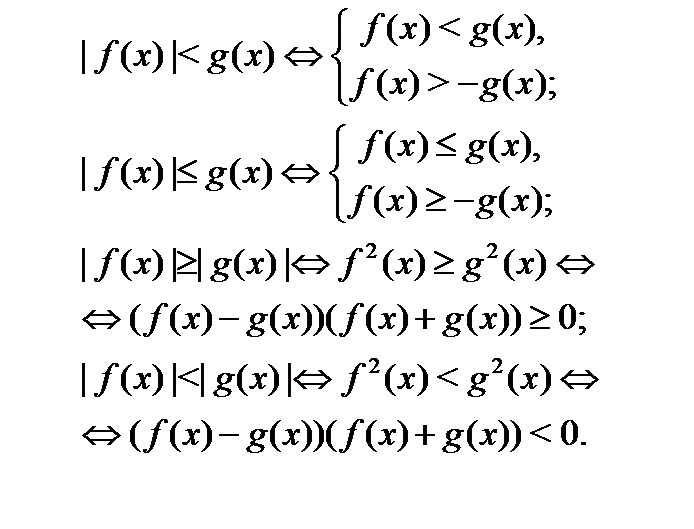
Пример 6. Решите неравенство:
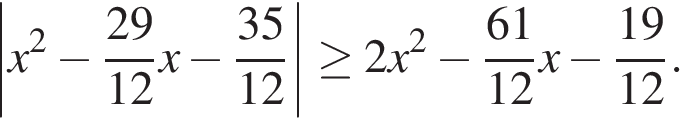
Согласно одной из стандартных схем неравенство равносильно совокупности неравенств:

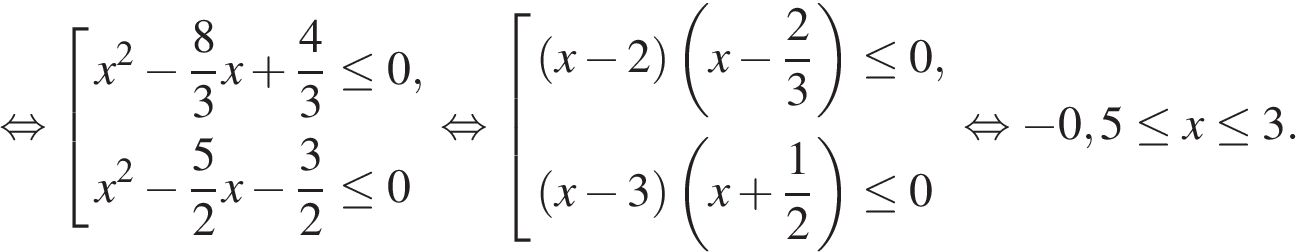
Ответ: 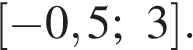
1.3.2 Для решения неравенств часто используют метод введения новой переменной, решают неравенство относительно этой переменной, а и затем решают полученные неравенства (или неравенство) с первоначальной переменной х.
Пример 7. Решите неравенство:

Сделаем замену 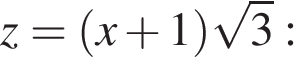 решим неравенство методом интервалов.
решим неравенство методом интервалов.
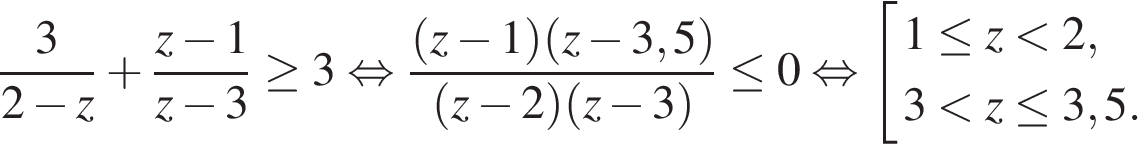
Возвратимся к исходной переменной и получим:
1  (х+1)
(х+1)  3
3  (х+1)
(х+1) 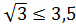
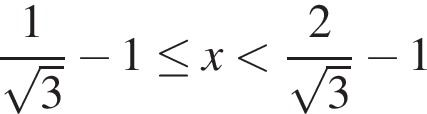 или
или 
Ответ: 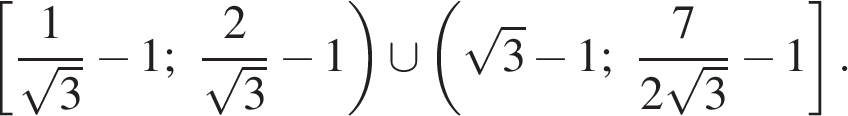
1.3.3 Разбиение области определения неравенства на подмножества Разбиение области определения неравенства на промежутки позволяет упростить некоторые неравенства. Решение неравенства рассматривают отдельно на каждом промежутке. Особенно наглядно этот метод работает при решении неравенств с модулями, когда модуль раскрываем на каждом промежутке.
Пример 8. Решите неравенство:

Числа 2 и -1 разбивают числовую прямую на три промежутка (-¥;1) ,
[1; 2) и [2; + ¥) . Освобождаясь от знаков модулей, с учетом знаков выражений под знаком модуля решим данное неравенство на каждом из этих промежутков.
Первый случай.
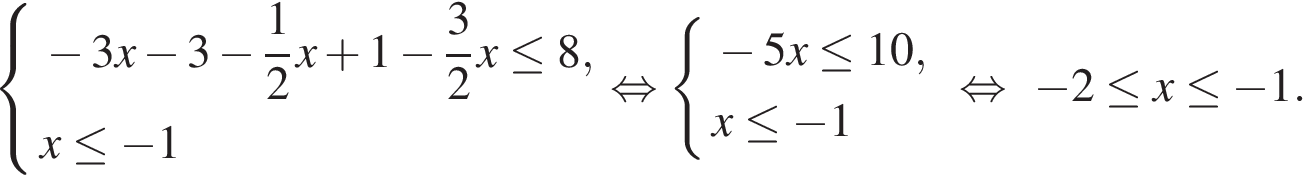
Второй случай.
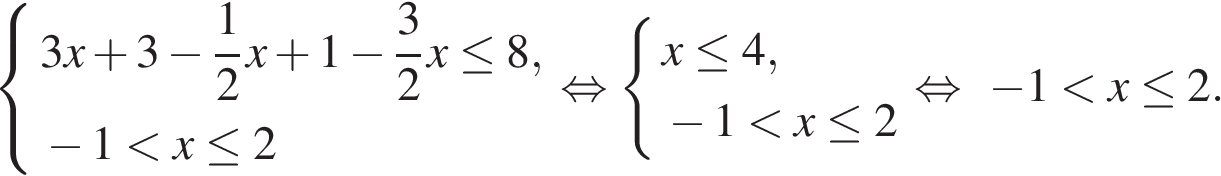
Третий случай.
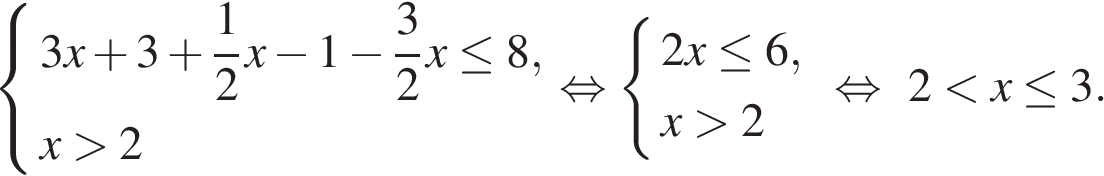
Объединяя промежутки, получаем 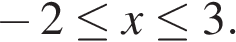
Ответ: 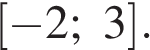
1.4 Геометрический подход в решении неравенств
Геометрические методы решения неравенств не часто используются на практике. Однако, геометрическая интерпретация неравенств позволяет легко и красиво решать, как простые, так и сложные задачи.
Пример 9. Решите неравенство: | x - 5 | > | x + 2 |.
Геометрическая интерпретация дает простое и красивое решение: так как |x - 5 | и | x + 2 | = | x - (-2) | – это расстояния от точки x до точек 5 и – 2 соответственно, то из данного равенства следует, что точка x – середина отрезка [-2;5], и поэтому х= 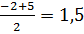 . Значит, решениями данного неравенства являются все числа x Î(-¥;1,5), т.е. все точки, расстояния от каждой из которых до точки 5 больше расстояния до точки (–2).
. Значит, решениями данного неравенства являются все числа x Î(-¥;1,5), т.е. все точки, расстояния от каждой из которых до точки 5 больше расстояния до точки (–2).
Ответ: (-¥;1,5).
В материалах для дистанционного обучения нашей группы в блоке «Методы решения уравнений. Модуль», представленном доцентом кафедры математического образования Конник О.Ю. этот подход развивается. Анализируя различные способы решения уравнений, содержащих модуль, Ольга Юрьевна делает вывод: обобщением решения вышеприведенных уравнений являются следующие равносильные переходы:
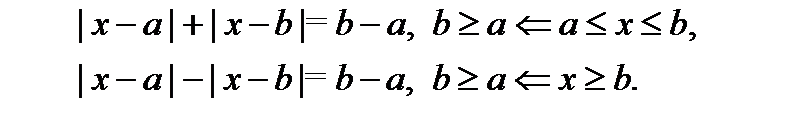 , которые можно использовать в решении неравенств.
, которые можно использовать в решении неравенств.
Пример 10. 1Решите неравенство: 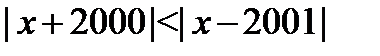 .
.
Решим неравенство, используя координатную прямую. Данное неравенство выполняется для всех точек c координатой х, которые находятся ближе к точке с координатой-2000, чем к точке с координатой -2001. Так как 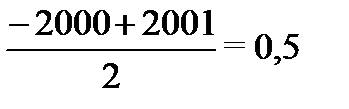 , то искомыми являются все точки, расположенные левее точки с координатой
, то искомыми являются все точки, расположенные левее точки с координатой 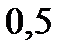 .
.
Ответ: 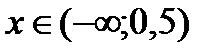 .
.
Глава 2. Алгебраические неравенства в контрольно-измерительных материалах государственной итоговой аттестации по математике
Все представленные выше методы используются при решении неравенств на государственной итоговой аттестации. В математике базового уровня задания с неравенствами однотипны: они на установление соответствия между неравенствами(простейшими) и их решениями. В математике профильного уровня неравенства могут встретиться в различных заданиях, но в основном они представлены в заданиях №13. Эти задания занимают одну из важнейших позиций в структуре КИМ. К их выполнению в 2015 г. приступало более 60% участников профильного единого государственного экзамена (ЕГЭ), а положительные баллы получили более 30% всех участников. Успешность выполнения заданий этого типа является характеристическим свойством, различающим базовый и профильный уровни подготовки учащихся. Поэтому при подготовке выпускников к экзамену решению заданий подобного уровня следует уделять много внимания.
2.1.1 Все задания, связанные с неравенствами, на базовом уровне (задания №17) зависимости от формы записи решений неравенств можно условно разделить на следующие прототипы: неравенства, в которых решения записаны в виде числовых промежутков, в виде неравенств, на геометрической модели.
- Решения записаны в виде числовых промежутков:
Поставьте в соответствие каждому неравенству множество его решений.
| НЕРАВЕНСТВА | РЕШЕНИЯ | |
А) 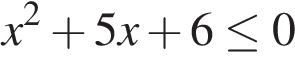 Б)
Б)  В)
В) 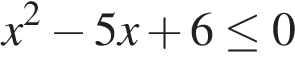 Г)
Г) 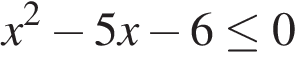
| 1) 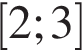 2)
2) 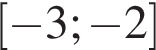 3)
3) 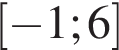 4)
4) 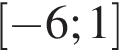
|
- Решения записаны в виде неравенств:
| НЕРАВЕНСТВА | РЕШЕНИЯ | |
А) 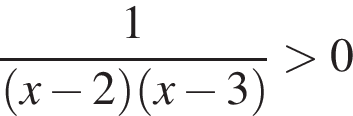 Б)
Б) 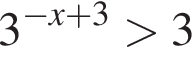 В)
В) 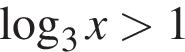 Г)
Г) 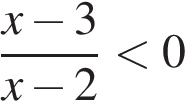
| 1)  или или  2)
2) 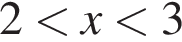 3)
3)  4)
4) 
|
-Решения представлены на числовой прямой:
| НЕРАВЕНСТВА | РЕШЕНИЯ | |
А) 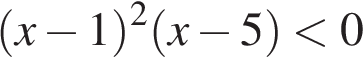 Б)
Б) 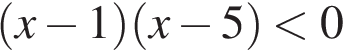 В)
В) 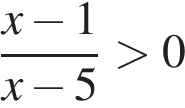 Г)
Г) 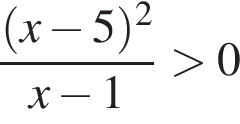
| 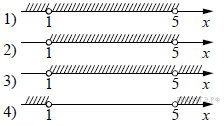
|
Чтобы ученик мог справиться с этими заданиями, надо отрабатывать различные формы записи ответа.
К типичным ошибкам можно отнести ошибки в расстановке знаков, ошибки в правильной записи луча, отрезка, интервала. Для профилактики таких ошибок можно использовать упражнения типа: «Составить неравенство, решение которого - (-∞, -10) U [-7, -4]», на которых отрабатываются эти понятия.
Рассматриваемые в этой работе рациональные, дробно-рациональные неравенства и неравенства, содержащие знак модуля, представленные в заданиях №13 профильного уровня можно условно разбить на прототипы.
К прототипу1 можно отнести неравенства, состоящие из алгебраических дробей, их суммы, произведения множителей. Например:
а) 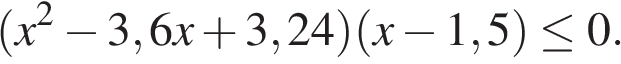
б) 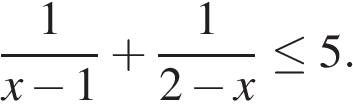
в) 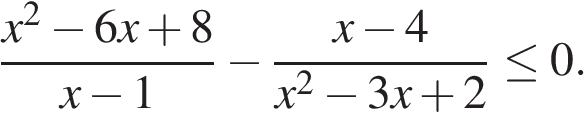
г) 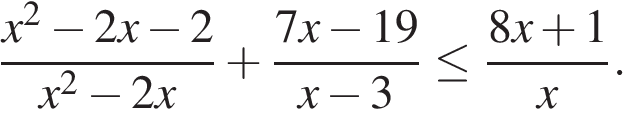
Такие неравенства надо преобразовать, чтобы свести их к решению методом интервалов (наиболее часто применяемый метод). Типичные ошибки в таких заданиях:
- последовательность шагов решения неверная или выполнена не до конца;
-формальное перенесение приемов решения уравнений на неравенство того же типа;
- не исключаются из ответа точки, в которых знаменатель обращается в 0;
-ошибки в расстановке знаков;
- в нестрогих неравенствах исключается из ответа точки (как правило, конечное их число), при которых числитель обращается в 0;
- последовательность шагов решения преобразования выполняются «в лоб» (например, алгебраические дроби складываются без учета разложения квадратного трехчлена на множители или по формуле), что приводит к тупиковой ситуации или неверному решению.
К прототипу 2 можно отнести сложные дробно-рациональные неравенства, которые решаются методом введения новых переменных.
а) 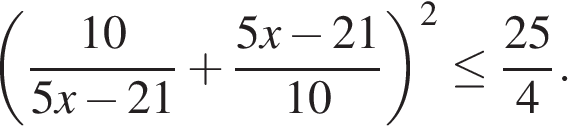
б) 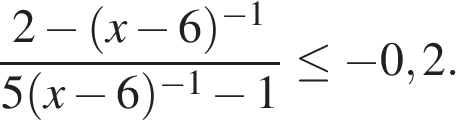
в) 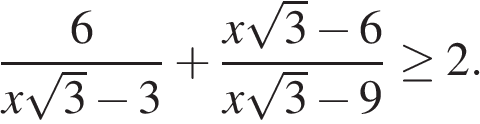
Типичные ошибки:
- используют преобразования, нарушающие равносильность;
- последовательность шагов решения выполнена не до конца (не выполнена обратная замена или ошибки в обратном переходе).
К прототипу 3 можно отнести неравенства, содержащие знак модуля, которые решаются методом равносильных переходов.

 К прототипу 4 можно отнести неравенства, содержащие знак модуля такого типа:
К прототипу 4 можно отнести неравенства, содержащие знак модуля такого типа:
Типичные ошибки:
- ошибки при применении равносильных переходов и в знаках при раскрытии модуля.
2.2.2К типичным ошибкам, относящимся ко всем неравенствам можно отнести неверное использование логической символики. Т.к. «конъюнкция» и «дизъюнкция» в школьном курсе математики не изучаются, зачастую эти символы применяются неверно, поэтому лучше их заменить словами «и», «или».
Чтобы ошибок при решении неравенств было меньше, необходима система устной работы для формирования вычислительной грамотности, которая в том числе поможет и безошибочно расставлять знаки в методе интервалов, нужно более тщательно отрабатывать применение метода введения вспомогательной переменной при решении неравенств, указывая на отличия от уравнений, решаемых тем же способом. Надо обращать внимание учащихся на то, что множество решений неравенства, полученного при введении вспомогательной переменной, целесообразно записать в виде одного или нескольких элементарных неравенств, в которых и возвращаться к исходной переменной. Запись же решений промежуточного неравенства в виде числовых промежутков часто не позволяет ученикам продолжить решение.
Учителю надо сформировать набор дидактических материалов по данной теме с учетом типичных ошибок и по индивидуальному маршруту совершенствовать с учащимися навыки решения неравенств.
Задача учителя-помочь ученику овладеть методикой решения неравенств, научился видеть «изюминки», тогда и решения получаются красивые, и результаты экзамена радуют.
Решите неравенство:
. 
Решение:
Преобразуем неравенство:
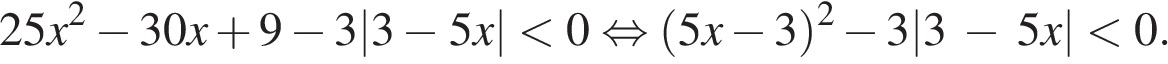
Сделав замену  получаем неравенство
получаем неравенство 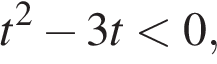 откуда
откуда 
Тогда: 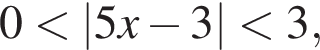 откуда
откуда 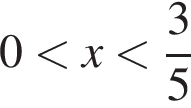 или
или 
Ответ: 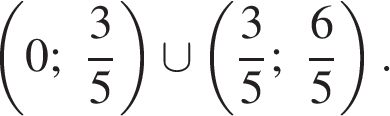
Заключение.
В своей работе я постаралась проанализировать изложение темы «алгебраические неравенства» в учебно-методической и научно-популярной литературе, систематизировать методы решения алгебраических неравенств по общему подходу к их решению (функциональный, алгебраический и геометрический подходы). Учитывая разнообразие неравенств, в данной работе были рассмотрены рациональные, дробно-рациональные неравенства и неравенства, содержащие знак модуля. Основные типы неравенств по данной теме, встречающиеся на государственной итоговой аттестации по математике, сгруппированы по прототипам, рассмотрены типичные ошибки каждой группы и способы их устранения.
Список использованных источников
1.Алгебра и начала анализа. 10-11 классы. В 2 частях. Ч. 1: Учебник для общеобразовательных учреждений. : учебник / Под. ред. А. Г. Мордковича. - М.: Мнемозина, 2013.
2. Алгебра и начала анализа. 10-11 классы. В 2 частях. Ч. 2: Задачник для общеобразовательных учреждений. : учебник / Под. ред. А. Г. Мордковича. - М.: Мнемозина, 2013.
3. Олехник С. Н. Уравнения и неравенства. Нестандартные методы решения. 10-11 классы : учебно-методическое пособие . - М.: Дрофа, 2004. - 192 с.
4.Прокофьев А. А., Корянов А. Г. Решение неравенств с одной переменной. Серия: Готовимся к ЕГЭ .-Р.Легион,2015,-93с.
5.Математика.Нестандартные методы решения неравенств и их систем/З.Л.Коронец, А.А.Коронец, Т.А.Алексеева_Орел,2012,-125с.
6.Прокофьев А.А., Корянов А.Г. Готовим к ЕГЭ хорошистов и отличников. Лекция 3. Решение неравенств алгебраическими методами. // Математика. – М., 2011, – №16, − С. 50-61
7.Прокофьев А.А., Корянов А.Г. Готовим к ЕГЭ хорошистов и отличников. Лекция 4. Решение неравенств функционально графическим методом. // Математика. – М., 2011, – №17, − С. 49-61.
Интернетресурсы
Математика ЕГЭ 2016 (открытый банк заданий)- www.mathege.ru
ЕГЭ по математике: подготовка к тестированию -www.alexlarin.narod.ru
ЕГЭ по математике: подготовка к тестированию- www. ege.sdamgia.ru
Открытый банк заданий ЕГЭ по математике на сайте- fipi.ru
Дата добавления: 2021-06-02; просмотров: 136; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
