Програмування графічним методом.
Розглянемо алгоритм розв’язування задач .лінійного програмування графічним методом .
1. Згідно з обмеженнями математичної моделі задачі побудувати ОПР. Для цого:
1.1. Всі обмеження - нерівності замінити рівняннями прямою заміною знаків “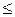 
” та “ 
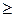” знаком “=”.
1.2. Кожне знайдене рівняння зобразити на площині прямою, яку будують за двома довільними точками. Кожна така пряма поділяє площину на дві півплощини – допустиму та недопустиму, а сама пряма є межею цих півплощин.
Щоб знайти допустиму півплощину, треба взяти дві довільні точки (по одній в кожній півплощині) та їх координати підставити до заданого обмеження. Точка, яка порушує знак обмеження, є точкою недопустимої півплощини, а точка, яка не порушує знака, - допустимої півплощини (для такого аналізу доцільно використовувати нульову точку, тобто початок координат).
1.3. Для кожного обмеження – нерівності виділити допустиму півплощину. Слід зауважити, що якщо математична модель містила обмеження – рівняння, то множина точок, які задовольняють обмеженню знаходиться на прямій, а не є півплощиною.
1.4. Після побудови всіх прямих і допустимих півплощин знайти ОПР, як перетин цих півплощин з урахуванням умови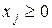 
.
Будьте уважними! Останнє обмеження 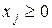означає, що вся область припустимих розв’ язків знаходиться в І координатній чверті!
2. Побудувати градієнт цільової функції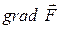 
.
Так як ми розглядаємо задачі лінійного програмування і цільова функція є лінійною, то координати градієнта цільової функції співпадають з її коефіцієнтами, тому в будь – якій точці координати градієнта однакові. Але для полегшення побудови градієнт краще будувати з початком в початку координат (тобто в точці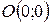 
). Тоді координати точки - кінця градієнта співпадають з координатами самого градієнта.
|
|
|
3. Побудувати пряму цільової функції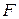 
(так звану гіперплощину), яка перпендикулярна градієнту цільової функції (наприклад, через початок координат, де 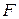=0).
4. Знайти місце розміщення оптимальних точок в допустимому просторі. Для цього побудовану пряму цільової функції зсунути за допомогою паралельного переносу вздовж градієнта і побудувати два її образи так, щоб ОПР знаходилась між ними і дотикалась їх. Зважаючи на те, що градієнт вказує в якому напрямку знаходиться точка максимуму, то з двох точок дотику перша точка в напрямку градієнта відповідає точці мінімуму, а друга – точці максимуму.
5. Знайти координати точок дотику ОПР. Для цього розв’язати системи рівнянь прямих, на перетині яких знаходяться ці точки. Результат розв’язування таких систем рівнянь дає оптимальні значення змінних.
|
|
|
6. Підставити у цільову функцію знайдені координати точок (оптимальні значення змінних) та знайти значення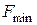 
або 
відповідно.
Зауваження:
§ Якщо серед обмежень математичної моделі є обмеження – рівняння, то ОПР є частина прямої (відрізок або промінь).
§ Якщо пряма цільової функції 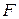розташовується паралельно одній з меж ОПР, то в цьому випадку задача має множину оптимальних розвязків з одним і тим самим значенням 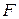( 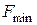чи відповідно). Будь – яка точка тієї частини границі ОПР (відрізку), яка паралельна гіперплощині є точкою відповідного екстремуму (максимуму або мінімуму). Для того, щоб знайти оптимальні розв’язки, необхідно знайти координати кінців відрізка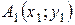 
та 
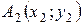, розв’язавши дві системи. Координати будь – якої точки 
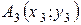, розташованої на відрізку 
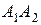знаходяться за формулою відрізка, а саме:
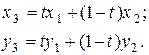
де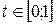 
- довільне число.
Приклади.
Приклад № 1. Знайти графічним методом оптимальний розв’язок задачі за такою математичною моделлю:
цільова функція
;
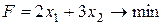обмеження:
.
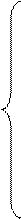
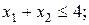
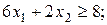
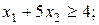
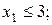
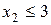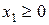і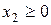 
.
Розв’язок:
Згідно з обмеженнями задачі, будуємо ОДР (рис. 4).
1. 
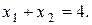
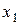
| 0 | 4 |
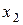
| 4 | 0 |
Множина точок, координати яких задовольняють нерівності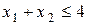 
, знаходиться нижче прямої 
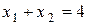, так як коефіцієнт біля змінної 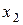додатний (1>0), а знак нерівності “ 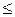” вказує на те, що це мають бути точки, які при однакових значеннях абсцис мають ординати менші, ніж відповідна точка на прямій .
|
|
|
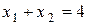2. 
|
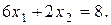
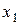
| 0 | 1 |
|
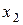
| 4 | 1 |
Множина точок, координати яких задовольняють нерівності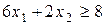 
, знаходиться вище прямої 
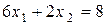, так як коефіцієнт біля змінної 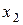додатний (2>0), а знак нерівності “ 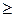” вказує на те, що це мають бути точки, які при однакових значеннях абсцис мають ординати більші, ніж відповідна точка на прямій .
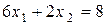3. 
|
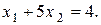
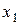
| -1 | 4 |
|
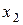
| 1 | 0 |
Множина точок, координати яких задовольняють нерівності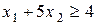 
, знаходиться вище прямої 
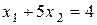, так як коефіцієнт біля змінної 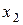додатний (5>0), а знак нерівності “ 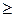” вказує на те, що це мають бути точки, які при однакових значеннях абсцис мають ординати більші, ніж відповідна точка на прямій .
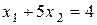4. 
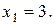
Ця пряма проходить паралельно вісі ординат через точку (3;0). Множина точок, яка задовольняє нерівності знаходиться зліва від прямої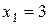 
, тому що нерівність має знак “ ”.
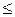5. 
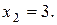
Ця пряма проходить паралельно вісі абсцис через точку (0;3). Множина точок, яка задовольняє нерівності знаходиться нижче прямої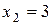 
, тому що нерівність має знак “ ”.
|
|
|
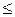Зважаючи на те, що математична модель має ще обмеження на змінн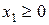і і 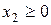, то область знаходиться тільки в першій координатній чверті.
Потім будуємо градієнт цільової функції 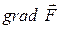- вектор з початком в точці 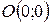та кінцем в точці (2;3), а потім – пряму цільової функції 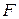перпендикулярно до побудованого градієнта. Побудовану пряму переміщуємо за допомогою паралельного переносу вздовж градієнта і будуємо два образи: 
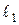та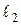 
між якими знаходиться побудована ОДР. Так як за умовою задачі, необхідно знайти 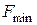, то це значення знаходиться в точці дотику образа 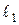з ОДР, тобто в точці М, яка утворюється прямими 
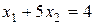та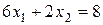 
. Розв’язуючи їх сумісно, знаходимо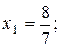 
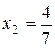, а значення цільової функції 
.
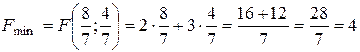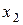
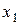
Рис. 4.
Відповідь: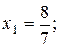 
, 
.
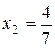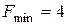Приклад № 2. Знайти графічним методом оптимальний розв’язок задачі, математична модель якої має вид:
цільова функція
;
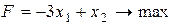обмеження:
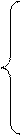
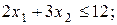
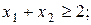
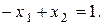
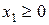і .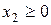
Розв’язок:
Згідно з обмеженнями задачі, будуємо ОДР (рис. 5).
1. 
|
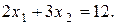
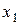
| 0 | 6 |
|
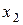
| 4 | 0 |
Множина точок, координати яких задовольняють нерівності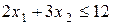 
, знаходиться нижче прямої 
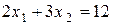, так як коефіцієнт біля змінної 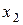додатний (3>0), а знак нерівності “ 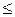” вказує на те, що це мають бути точки, які при однакових значеннях абсцис мають ординати менші, ніж відповідна точка на прямій .
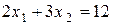2. 
|
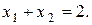
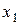
| 0 | 2 |
|
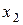
| 2 | 0 |
Множина точок, координати яких задовольняють нерівності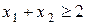 
, знаходиться вище прямої 
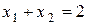, так як коефіцієнт біля змінної 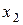додатний (1>0), а знак нерівності “ 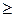” вказує на те, що це мають бути точки, які при однакових значеннях абсцис мають ординати більші, ніж відповідна точка на прямій .
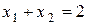3.
|
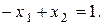
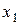
| 0 | -1 |
|
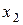
| 1 | 0 |
Множина точок, координати яких задовольняють рівнянню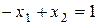 
знаходиться на прямій! Тому ОДР – це є відрізок АВ.
Потім будуємо градієнт цільової функції 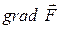- вектор з початком в точці 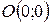та кінцем в точці (-3;1), а після цього – пряму цільової функції 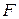перпендикулярно до побудованого градієнта. Побудовану пряму переміщуємо за допомогою паралельного переносу вздовж градієнта і будуємо два образи: 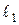та 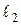між якими знаходиться відрізок АВ. Один з кінців відрізка відповідає мінімуму, а інший кінець – максимуму цільової функції. Так як за умовою задачі, необхідно знайти 
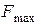, то це значення знаходиться в точці А, яка утворюється прямими 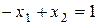та 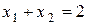. Розв’язуючи їх сумісно, знаходимо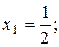 
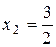, а значення цільової функції 
.
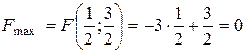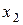
Рис. 5.
Відповідь: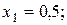 
. 
.
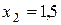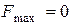Приклад № 3. Знайти графічним методом оптимальний розв’язок задачі математична модель якої має вид:
цільова функція
;
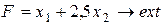обмеження:
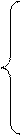
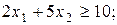
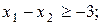
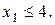
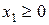і .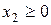
Розв’язок:
Згідно з обмеженнями задачі, будуємо ОДР (рис. 6).
1. 
.
|
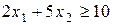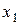
| 0 | 5 |
|
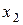
| 2 | 0 |
Множина точок, координати яких задовольняють нерівності 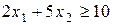, знаходиться вище прямої 
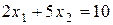, так як коефіцієнт біля змінної 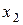додатний (5>0), а знак нерівності “ 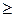” вказує на те, що це мають бути точки, які при однакових значеннях абсцис мають ординати більші, ніж відповідна точка на прямій .
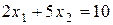2. 
.
|
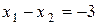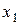
| 0 | -3 |
|
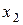
| 3 | 0 |
Множина точок, координати яких задовольняють нерівності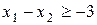 
, знаходиться нижче прямої 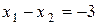, так як коефіцієнт біля змінної 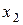від’ємний (-1<0). Від’ємний коефіцієнт біля змінної 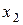вказує на те, що треба змінити напрямок розташування точок, які задовольняють нерівності, тобто знак нерівності “ 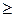” вказує на те, що це мають бути точки, які при однакових значеннях абсцис мають ординати не більші, а менші, ніж відповідна точка прямої .
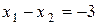3. 
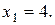
Ця пряма проходить паралельно вісі ординат через точку (4;0). Множина точок, яка задовольняє нерівності знаходиться зліва від прямої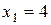 
, тому що нерівність має знак “ ”.
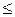Зверніть увагу на те, що математична модель має обмеження на змінн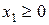і і 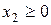, тобто область знаходиться тільки в першій координатній чверті. ОДР є чотирикутник АВСД.
Побудуємо тепер градієнт цільової функції 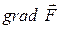з початком в точці 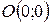та кінцем в точці (1;2,5). Після цього будуємо пряму цільової функції 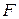перпендикулярно до градієнта. Побудовану пряму переміщуємо за допомогою паралельного переносу вздовж градієнта і будуємо два образи: 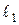та 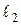між якими знаходиться побудована ОДР. Так як за умовою задачі, необхідно знайти 
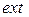, то це означає, що необхідно вказати точки мінімуму і максимуму, а також знайти відповідні значення цільових функцій 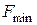та 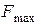. З рисунку (6) видно, що образ 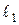, який відповідає мінімуму, співпадає з відрізком АД області, тобто дотиком є не кутова точка області, а цілий відрізок. Це означає, що задача має альтернативний мінімум, тобто точкою мінімуму є будь – яка точка відрізку АД. Знайдемо координати точок А і Д.
Точка А: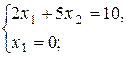 
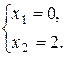А(0;2).
Точка Д: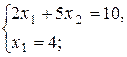 
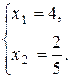Д(4;0,4).
Координати будь – якої точки, що знаходиться на відрізку АД можуть бути знайдені за формулами:
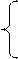
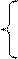
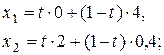тобто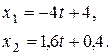 
де 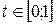- довільне число.
Таким чином,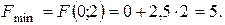 
Так як образ гіперплощини 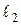дотикається ОДР в одній точці С, то значить цільова функція має один максимум.
Точка С: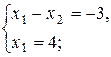 
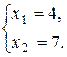С(4;7).
Тому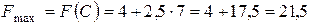 
Рис. 6.
Відповідь: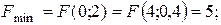 
.
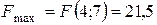Завдання для самостійного розв’язування.
Розв’язати графічним методом задачу, математична модель якої вже відома.
Варіант 1.
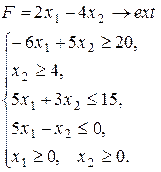
Варіант 3.
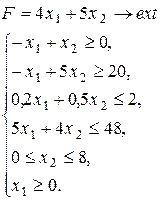
Варіант 5.
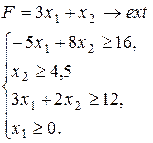
Варіант 7.
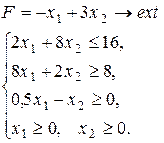
Варіант 2.
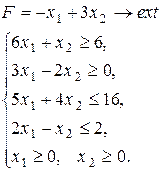
Варіант 4.
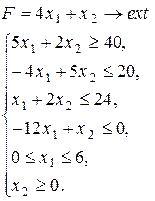
Варіант 6.
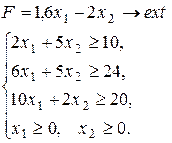
Варіант 8.
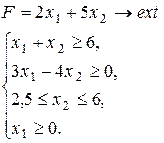
Варіант 9.
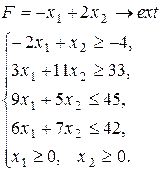
Варіант 11.
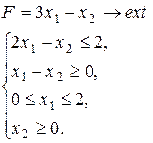
Варіант 13.
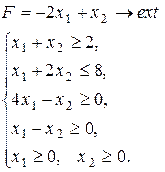
Варіант 15.
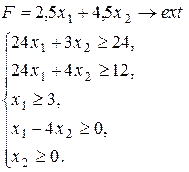
Варіант 10.
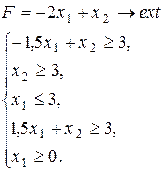
Варіант 12.
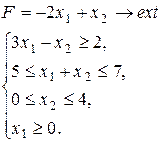
Варіант 14.
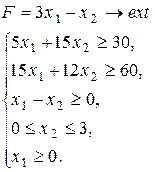
Варіант 16.
Варіант 17.
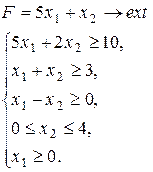
Варіант 19.
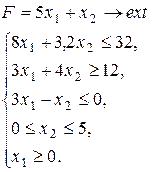
Варіант 21.
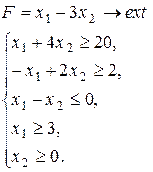
Варіант 23.
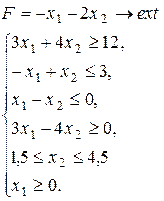
Варіант 18.
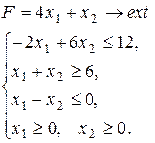
Варіант 20.
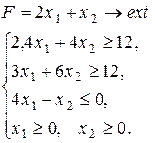
Варіант 22.
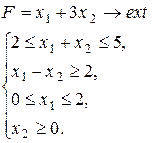
Варіант 24.
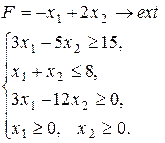
Варіант 25.
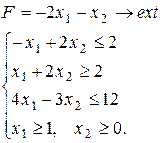
Варіант 26.
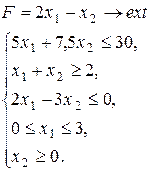
Варіант 28.
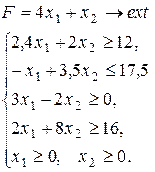
Варіант 30.
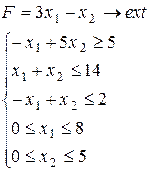
Варіант 27.
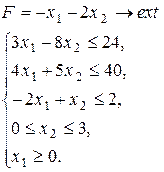
Варіант 29.
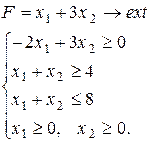
Література.
1. І. Акулич И.Л. Математическое программирование в примерах и задачах. - М.: Высш. шк., 1986.
2. Костевич Д.С., Лапко А.А. Теория игр. Исследование операций. - Минск: Вышейш. шк., 1982.
3. Кузнецов Ю.Н., Кузубов В.М., Волощенко А.Б. Математическое программирование. - М.: Высш. шк., 1985.
4. Кузнецов А.В, Холод Н.И. Математическое программирование. - Минск: Вышейш. шк., 1984.
5. Сакович В.А. Исследование операций. - Минск: Вышейш. шк., 1985.
6. Щербак А.Ф. Математичне програмування, ч.1-2, КФ КДЕУ,1994.
7. Щербак А.Ф. Збірник задач з математичного програмування. – КЕІ КНЕУ, 1999.
8. Щербак А.Ф., Глоба Н.Г., Нєвєров С.Л., Ковтун Р.Х., Щербак Т.А. Вироб ничі ситуації з використанням методів оптимізації та ЕОМ. – КЕІ КНЕУ, 2001.
9. Щербак А.Ф., Глоба Н.Г. Методичні вказівки до самостійної роботи студентів та розв’язування задач з дисципліни “Дослідження операцій та дискретний аналіз”, ч.1-2, - КЕІ КНЕУ, 2001.
Дата добавления: 2021-03-18; просмотров: 70; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!