Свойства биномиальных коэффициентов.
Лекция № 9. Формула бинома Ньютона. Свойства биноминальных коэффициентов. Треугольник Паскаля.
Формула бинома Ньютона
Определение.
Бино́м Нью́то́на — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид. где. — биномиальные коэффициенты, — неотрицательное целое число.
Для натуральных n имеет вид
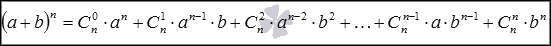, где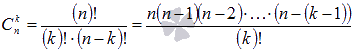 
- биномиальные коэффициенты, представляющие из себя сочетания из n по k, k=0,1,2,…,n, "!" – это знак факториала).
Пример.
Формула сокращенного умножения "квадрат суммы" раскладывается согласно формуле бинома Ньютона:
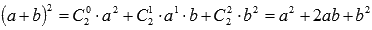
т.е.представляет собой частный случай бинома Ньютона при n=2.
Примечание.
- выражение в правой части формулы бинома Ньютона, называют разложением выражения (a+b)n;
- выражение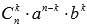 
называют (k+1) -ым членом разложения, k=0,1,2,…,n.
Коэффициенты бинома Ньютона, свойства биномиальных коэффициентов, треугольник Паскаля.
Треугольник Паскаля.
Биномиальные коэффициенты для различных n удобно представлять в виде таблицы, которая называется арифметический треугольник Паскаля.
В общем виде треугольник Паскаля имеет следующий вид:
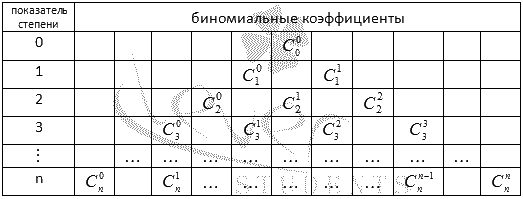
Треугольник Паскаля чаще встречается в виде значений коэффициентов бинома Ньютона для натуральных n:
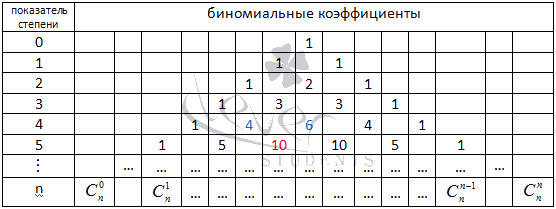
Боковые стороны треугольника Паскаля состоят из единиц. Внутри треугольника Паскаля стоят числа, получающиеся сложением двух соответствующих чисел над ним. Например, значение десять (выделено красным) получено как сумма четверки и шестерки (выделены голубым). Это правило справедливо для всех внутренних чисел, составляющих треугольник Паскаля, и объясняется свойствами коэффициентов бинома Ньютона.
|
|
|
Свойства биномиальных коэффициентов.
Для коэффициентов бинома Ньютона справедливы следующие свойства:
· коэффициенты, равноудаленные от начала и конца разложения, равны между собой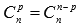 
, p=0,1,2,…,n;
· 
;
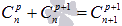· сумма биномиальных коэффициентов равна числу 2, возведенному в степень, равную показателю степени бинома Ньютона: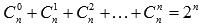 
;
· сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме биномиальных коэффициентов, стоящих на нечетных местах.
Бином Ньютона - применение при решении примеров.
Пример 1.
Напишите разложение выражения (a+b)5 по формуле бинома Ньютона.
Решение.
Смотрим на строку треугольника Паскаля, соответствующую пятой степени (п.2.1). Биномиальными коэффициентами будут числа 1, 5, 10, 10, 5, 1.
Таким образом, имеем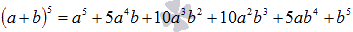 
.
Пример 2.
Найдите коэффициент бинома Ньютона для шестого члена разложения выражения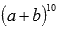 
.
|
|
|
Решение.
В нашем примере n=10, k=6-1=5. Таким образом, мы можем вычислить требуемый биномиальный коэффициент:
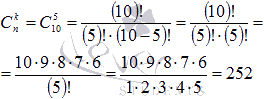
Пример 3.
Доказать, что значение выражения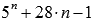 
, где n – натуральное число, делится на 16 без остатка.
Решение.
Представим первое слагаемое выражение как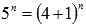 
и воспользуемся формулой бинома Ньютона:
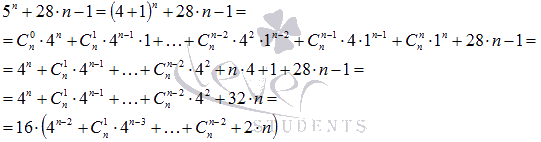
Полученное произведение доказывает делимость исходного выражения на 16 , без остатка.
Пример 4.
Возведите в степень выражение – (х2 - 2y)5
Решение.
Согласно формуле бинома Ньютона имеем:
- (a+b)n = (х2 - 2y)5;
- a = х2;
- b = - 2y.
Раскладываем по формуле бинома Ньютона:
С50*(х2)5 + С51*(х2)4 * (-2y) + С52*(х2)3 * (-2y)2 + С53*(х2)2 * (-2y)3 + С54*(х)2 * (-2y)4 + С55* (-2y)5
По треугольнику Паскаля для n = 5 (см. п.2.1) определяем значения биноминальных коэффициентов:
С50 = 1; С51 = 5; С52 = 10; С53 = 10; С54 = 5; С55 = 1;
Подставляем в формулу бинома Ньютона:
1*(х)10 + 5*(х)8 * (-2y) + 10*(х)6 * (-2y)2 + 10*(х)4 * (-2y)3 + 5*(х)2 * (-2y)4 + 1* (-2y)5
Задание 1 . Найдите коэффициент бинома Ньютона для члена разложения выражения 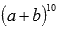. (№ члена разложения указан в таблице; № варианта равен № в классном журнале).
| № варианта | Исходные данные | № варианта | Исходные данные | |||
| Вариант 1 | k = 5 | Вариант 13
| k = 10 | |||
| Вариант 2 | k = 4 | Вариант 14 | k = 4 | |||
| Вариант 3 | k = 8 | Вариант 15 | k = 8 | |||
| Вариант 4 | k = 10 | Вариант 16 | k = 7 | |||
| Вариант 5 | k = 6 | Вариант 17 | k = 8 | |||
| Вариант 6 | k = 7 | Вариант 18 | k = 10 | |||
| Вариант 7 | k = 8 | Вариант 19 | k = 7 | |||
| Вариант 8 | k = 12 | Вариант 20 | k = 9 | |||
| Вариант 9 | k = 4 | Вариант 21 | k = 5 | |||
| Вариант 10 | k = 7 | Вариант 22 | k = 4 | |||
| Вариант 11 | k = 9 | Вариант 23 | k = 8 | |||
| Вариант 12 | k = 14 | Вариант 24 | k = 12 | |||
Задание 2 . Возведите в степень выражение – (a + b)n
| № варианта | Исходные данные | № варианта | Исходные данные | |||
| Вариант 1 | (4x + 2y); n = 5 | Вариант 13 | (4x3 + 2y2); n = 3 | |||
| Вариант 2 | (x3 - y); n = 4 | Вариант 14 | (x + 2y4); n = 4 | |||
| Вариант 3 | (4x2 + 8y); n = 6 | Вариант 15 | (4x - 10y); n = 5 | |||
| Вариант 4 | (x – y2); n = 4 | Вариант 16 | (8x + 2y); n = 6 | |||
| Вариант 5 | (4x2 + y); n = 6 | Вариант 17 | (4x2 - y); n = 5 | |||
| Вариант 6 | (x2 – y2); n = 4 | Вариант 18 | (x + 2y2); n = 5 | |||
| Вариант 7 | (5x – y); n = 5 | Вариант 19 | (4x3 + y); n = 4 | |||
| Вариант 8 | (x + 2y); n = 6 | Вариант 20 | (x + 8y); n = 6 | |||
| Вариант 9 | (2x3 - 4y); n = 3
| Вариант 21 | (5x2 + y3); n = 3 | |||
| Вариант 10 | (8x2 – y); n = 4 | Вариант 22 | (x2 - 6y); n = 5 | |||
| Вариант 11 | (8x – 10y); n = 5 | Вариант 23 | (4x + 9y3); n = 3 | |||
| Вариант 12 | (x2 + y); n = 6 | Вариант 24 | (x2 + 2y); n = 5 | |||
ДЗ – конспект (контрольные вопросы):
1. Бино́м Нью́то́на – определение, примечание.
2. Порядок заполнения треугольника Паскаля значениями биноминальных коэффициентов (п. 2.1, после 2-й таблицы).
Свойства биномиальных коэффициентов.
4. Решить вариант задания №1 и №2.
Дата добавления: 2021-03-18; просмотров: 427; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!