Выбор формы уравнения регрессии
Особенности эконометрического метода
Эконометрический метод складывался в преодолении следующих неприятностей, искажающих результаты применения классически статистических методов:
1) асимметричность связей;
2) мультиколлинеарность объясняющих переменных;
3) закрытость механизма связи между переменными в изолированной регрессии;
4) эффект гетероскедастичности, т.е. отсутствие нормального распределения остатков для регрессионной функции;
5) автокорреляция;
6) ложная корреляция;
7) наличие лагов.
Эконометрическое исследование заключается в решении следующих проблем:
1) качественный анализ связей экономических переменных – выделение зависимых и независимых переменных;
2) изучение соответствующего раздела экономической теории;
3) подбор данных;
4) спецификация формы связи между зависимыми и независимыми переменными;
5) оценка параметров модели;
6) проверка ряда гипотез о свойствах распределения вероятностей для случайной компоненты (гипотезы о средней дисперсии и ковариации);
7) анализ мультиколлинеарности объясняющих переменных, оценка ее статистической значимости, выявление переменных, ответственных за мультиколлинеарность;
8) введение фиктивных переменных;
9) выявление автокорреляции, лагов;
10) выявление тренда, циклической и случайной компонент;
11) проверка остатков на гетероскедастичность;
12) анализ структуры связей и построение системы одновременных уравнений;
|
|
|
13) проверка условия идентификации;
14) оценивание параметров системы одновременных уравнений (двухшаговый и трехшаговый метод наименьших квадратов, метод максимального правдоподобия);
15) моделирование на основе системы временных рядов: проблемы стационарности и коинтеграции;
16) построение рекурсивных моделей, авторегрессионных моделей;
17) проблема идентификации и оценивания параметров.
этапы эконометрического исследования можно указать:
1. Постановка проблемы.
2. Получение данных, анализ их качества.
3. Спецификация модели.
4. Оценка параметров.
5. Интерпретация результатов.
№2.
К простейшим показателям степени тесноты связи относят коэффициент корреляции знаков, который был предложен немецким ученым Г.Фехнером
Этот показатель основан на оценке степени согласованности направлений отклонений индивидуальных значений факторного и результативного признаков от соответствующих средних.
na – число совпадений знаков отклонений индивидуальных величин от средней, nb – число несовпадений знаков отклонений, то коэффициент Фехнера
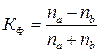
Более совершенным показателем степени тесноты связи является линейный коэффициент корреляции (r).
|
|
|
При расчете этого показателя учитываются не только знаки отклонений индивидуальных значений признака от средней, но и сама величина таких отклонений, Т.е. соответственно для факторного и результативного признаков величины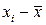 
и 
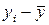. Однако непосредственно сопоставлять между собой полученные абсолютные величины нельзя, так как сами признаки могут быть выражены в разных единицах (как это имеет место в представленном примере), а при наличии одних и тех же единиц измерения средние могут быть различны по величине. В этой связи сравнению могут подлежать отклонения, выраженные в относительных величинах, т.е. в долях среднего квадратического отклонения (их называют нормированными отклонениями). Так, для факторного признака будем иметь совокупность величин 
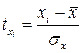, а для результативного 
.
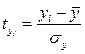Для того чтобы на основе сопоставления рассчитанных нормированных отклонений получить обобщающую характеристику степени тесноты связи между признаками для всей совокупности, рассчитывают среднее произведение нормированных отклонений. Полученная таким образом средняя и будет являться линейным коэффициентом корреляции r.
|
|
|
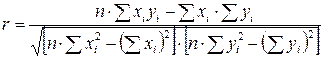
При пользовании этой формулой отпадает необходимость вычислять отклонения индивидуальных значений признаков от средней величины, что исключает ошибку в расчетах при округлении средних величин.
Линейный коэффициент корреляции может принимать любые значения в пределах от –1 до +1. Чем ближе коэффициент корреляции по абсолютной величине к +1, тем теснее связь между признаками. Знак при линейном коэффициенте корреляции указывает на направление связи – прямой зависимости соответствует знак плюс, а обратный зависимости – знак минус.
Если с увеличением значений факторного признака х, результативный признак у имеет тенденцию к увеличению, то величина коэффициента корреляции будет находиться между 0 и 1. Если же с увеличением значений х результативный признак у имеет тенденцию к снижению, коэффициент корреляции может принимать значения в интервале от 0 до –1.
Квадрат коэффициента корреляции (r2) носит название коэффициента детерминации. Для рассматриваемого примера его величина равна 0,6569, а это означает, что 65,69% вариации числа клиентов, воспользовавшихся услугами фирмы, объясняется вариацией затрат фирм на рекламу своих услуг.
|
|
|
Оценка значимости коэф кореляции
При большом объеме выборки из нормально распределенной совокупности можно считать распределение линейного коэффициента корреляции приближенно нормальным со средней, равной r и дисперсией
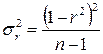, (1.8)
откуда средняя квадратическая ошибка коэффициента корреляции:
,
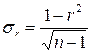Доверительный интервал для коэффициента корреляции будет записан так:
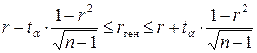, (1.10)
где rген – значение коэффициента корреляции в генеральной совокупности.
В нашем примере s r = 0,0787; t a(0,05, 18) = 2,1; D = 0,1654 и пределы коэффициента корреляции: от 0,6451 до 0,9759.
При малых объемах выборки и линейном коэффициенте корреляции, близким к 1, использование средней квадратической ошибки по формуле в качестве критерия существенности r оказывается невозможным в силу того, что распределение выборочного r может значительно отличаться от нормального.
2. Для малого объема выборочной совокупности используется тот факт, что величина
при условии r = 0, распределена по закону Стьюдента с (n –2) степенями свободы.
Полученную величину tрасч сравнивают с табличным значением t-критерия (число степеней свободы равно n –2). Если рассчитанная величина превосходит табличную, то практически невероятно, что найденное значение обусловлено только случайными совпадениями x и y в выборке из генеральной совокупности, для которой действительное значение коэффициента корреляции равно нулю. Если же вычисленная величина меньше, чем табличная, то полагают, что коэффициент корреляции в генеральной совокупности в действительности равен нулю и соответственно эмпирический коэффициент корреляции существенно не отличается от нуля.
№3.
Коэффициенты корреляции, основанные на использовании рангов, были предложены К. Спирмэном и М.Кендэлом. Коэффициент корреляции рангов Спирмэна основан на рассмотрении разности рангов значений факторного и результативного признаков.
Формула коэффициента корреляции рангов Спирмэна, который обозначают r:
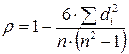(1.11)
где di = xi – yi – разность между рангами исходных переменных x и y.
Поскольку коэффициенты корреляции рангов могут изменяться в пределах от –1 до +1 (как и линейный коэффициент корреляции), по результатам расчетов коэффициента Спирмэна можно предположить наличие достаточно тесной прямой зависимости между x и y.
Существует специальная таблица предельных значений коэффициентов корреляции рангов Спирмэна при условии верности нулевой гипотезы об отсутствии корреляционной связи при заданном уровне значимости и определенном объеме выборочных данных.
По такой таблице находим, что при объеме выборки в 10 единиц (n = 10) и уровне значимости 5% (a = 0,05) критическая величина для рангового коэффициента корреляции составляет ± 0,6364. Это означает, что вероятность получить величину коэффициента r, превышающую критическое значение при условии верности нулевой гипотезы, будет менее 5%.
М.Кендэл предложил еще одну меру связи между переменными xi и yi – коэффициент корреляции рангов Кендэла – t:
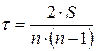, где S = P + Q. (1.12)
Для вычисления t надо упорядочить ряд рангов переменной х, приведя его к ряду натуральных чисел. Затем рассматривают последовательность рангов переменной у
Для нахождения суммы S находят два слагаемых Р и Q. При определении слагаемого Р нужно установить, сколько чисел, находящихся справа от каждого из элементов последовательности рангов переменной у, имеют величину ранга, превышающую ранг рассматриваемого элемента. Так, например, первому значению в последовательности рангов переменной у, т.е. числу 2, соответствует 8 чисел (7, 6, 3, 4, 5, 9, 10, 8), которые превышают ранг 2; второму значению 1 соответствует также 8 чисел(7, 6, 3, 4, 5, 9, 10, 8); превышающих 1 и т.д. Суммируя полученные таким образом числа, мы получим слагаемое Р, которое можно рассматривать как меру соответствия последовательности рангов переменной у последовательности рангов переменных х. Для нашего примера Р = 35 (8+8+3+3+5+4+3+1).
Второе слагаемое Q характеризует степень несоответствия последовательности рангов переменной у последовательности рангов переменной х. Чтобы определить Q подсчитаем, сколько чисел, находящихся справа от каждого из членов последовательности рангов переменной у имеет ранг меньше, чем эта единица. Такие величины берутся со знаком минус.
В рассматриваемом примере Q = –10 (–1 –0 –4 –3 –0 –0 –0 –1 –1)
Следовательно, S = P + Q = 35 – 10 = 25.
Коэффициент корреляции рангов Кендэла в нашем примере равен:
.
Коэффициент Кендэла также изменяется в пределах от –1 до +1 и равен нулю при отсутствии связи между рядами рангов.
Вычисляем коэффициент ранговой корреляции Фехнера по формуле
.
№4.
Сводится линейная регрессия к нахождению уравнения вида
.
Построение линейной регрессии сводится к оценке ее параметров – a и b. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).
Этот метод позволяет получить такие оценки параметров a и b, при которых сумма квадратов отклонений фактических значений результативного признака от расчетных (теоретических) минимальна:
.
система нормальных уравнений для оценки параметров a и b:
.
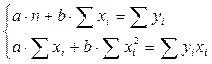
Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.
Знак при коэффициенте регрессии b показывает направление связи: при b > 0 – связь прямая, при b < 0 – обратная.
Формально а – значение у при х = 0. Если признак-фактор не имеет и не может иметь нулевого значения, то трактовка свободного члена а не имеет смысла. Параметр а может не иметь экономического содержания. Попытки экономически интерпретировать параметр а могут привести к абсурду, особенно при а < 0.
Интерпретировать можно лишь знак при параметре а. Если а > 0, то относительное изменение результата происходит медленнее, чем изменение фактора
Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции rxy.
Как известно, линейный коэффициент корреляции находится в границах –1 £ rxy £ 1. Если коэффициент регрессии b > 0, то 0 £ rxy £ 1, и, наоборот, при b < 0 –1 £ rxy £ 0.
,
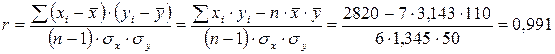Коэффициент детерминации характеризует долю дисперсии результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака:
. (2.10)
Соответственно величина 1 – r 2 характеризует долю дисперсии у, вызванную влиянием остальных не учтенных в модели факторов.
Величина коэффициента детерминации является одним из критериев оценки качества линейной модели. Чем больше доля объясненной вариации, тем соответственно меньше роль прочих факторов и, следовательно, линейная модель хорошо аппроксимирует исходные данные, и ею можно воспользоваться для прогноза значений результативного признака.
Линейный коэффициент корреляции по содержанию отличается от коэффициента регрессии. Выступая показателем силы связи, коэффициент регрессии b на первый взгляд может быть использован как измеритель ее тесноты.
лин коэффициент корреляции:
Его величина выступает в качестве стандартизованного коэффициента регрессии и характеризует среднее в сигмах (s y)изменение результата с изменением фактора на одну s x.
Линейный коэффициент корреляции как измеритель тесноты линейной связи признаков логически связан не только с коэффициентом регрессии b , но и с коэффициентом эластичности, который является показателем силы связи, выраженным в процентах. При линейной связи признаков х и у средний коэффициент эластичности в целом по совокупности определяется как 
,т. е. его формула по построению близка к формуле линейного коэффициента корреляции 
.
Несмотря на схожесть этих показателей, измерителем тесноты связи выступает линейный коэффициент корреляции (rxy)а коэффициент регрессии (b у/х)и коэффициент эластичности (Эу/х) – показатели силы связи: коэффициент регрессии является абсолютной мерой, ибо имеет единицы измерения, присущие изучаемым признакам у и х, а коэффициент эластичности – относительным показателем силы связи, потому что выражен в процентах.
№5.
Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера.
Непосредственному расчету F-критерия предшествует анализ дисперсии.
;
;
.
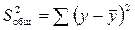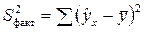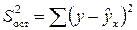Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим средний квадрат отклонений или дисперсию на одну степень свободы S2 и вытекающую из нее стандартную ошибку S.
.
Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F-отношения, т.е.критерий F:
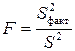
F-статистика используется для проверки нулевой гипотезы H0: S2факт = S2.
Если нулевая гипотеза H0 справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Если H0 несправедлива, то факторная дисперсия превышает остаточную в несколько раз. Английским статистиком Снедекором разработаны таблицы критических значений F-отношений при разных уровнях значимости нулевой гипотезы и различном числе степеней свободы. Табличное значение F-критерия – это максимальная величина отношений дисперсий, которая может иметь место при случайном расхождении их для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение F-отношения признаётся достоверным (отличным от единицы), если оно больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи:
Fфакт > Fтабл, H0 отклоняется.
Если же величина F окажется меньше табличной, то вероятность нулевой гипотезы выше заданного уровня (например, 0,05) и она не может быть отклонена без риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым: Fфакт < Fтабл, H0 не отклоняется.
Величина F-критерия связана с коэффициентом детерминации r2.
Тогда значение F-критерия можно выразить следующим образом:
.
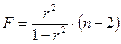В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка: mb и ma.
Для оценки значимости коэффициента регрессии его величину сравнивают с его стандартной ошибкой, т.е. определяют фактическое значение t-критерия Стьюдента:
,
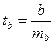которое затем сравнивают с табличным значением при определенном уровне значимости a и числе степеней свободы (n – 2).
Поскольку коэффициент регрессии b в эконометрических исследованиях имеет четкую экономическую интерпретацию, доверительные границы интервала для коэффициента регрессии не должны содержать противоречивых результатов, например, – 10 £ b £ 40. Такого рода запись показывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже нуль, чего не может быть.
Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции mr:
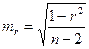. (2.19)
Фактическое значение t-критерия Стьюдента определяется как
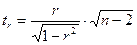. (2.20)
Данная формула свидетельствует, что в парной линейной регрессии t2r = F, ибо, как уже указывалось,
.
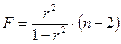Кроме того, t2b = F, следовательно, t2r = t2b.
Таким образом, проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о значимости линейного уравнения регрессии.
№6. Интервальный прогноз на основе линейного уравнения регрессии
В прогнозных расчетах по уравнению регрессии определяется предсказываемое yr значение как точечный прогноз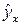 
при x р = xk. т.е. путем подстановки в линейное уравнение регрессии 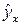= a + b × x соответствующего значения x. Однако точечный прогноз явно нереален, поэтому он дополняется расчетом стандартной ошибки 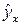, т.е. 
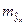и соответственно мы получаем интервальную оценку прогнозного значения y*:
.
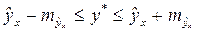
Отсюда следует, что стандартная ошибка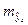 
зависит от ошибки 
и ошибки коэффициента регрессии b, т.е.
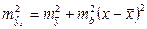(2.23)
Из теории выборки известно, что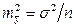 
. Используя в качестве оценки s2 остаточную дисперсию на одну степень свободы S2, получим формулу расчета ошибки среднего значения переменной y:
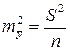. (2.24)
Ошибка коэффициента регрессии, как уже было показано, определяется формулой
.
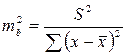Считая, что прогнозное значение фактора xp = xk, получим следующую формулу расчета стандартной ошибки предсказываемого по линии регрессии значения, т.е. :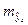
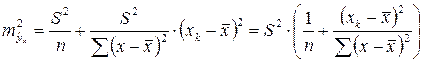. (2.25)
Соответственно 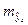имеет выражение:
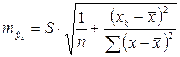. (2.26)
Рассмотренная формула стандартной ошибки предсказываемого среднего значения y при заданном значении xk характеризует ошибку положения линии регрессии. Величина стандартной ошибки 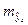достигает минимума при xk = x и возрастает по мере того, как «удаляется» от x в любом направлении. Иными словами, чем больше разность между xk и x, тем больше ошибка 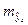, с которой предсказывается среднее значение y для заданного значения xk. Можно ожидать наилучшие результаты прогноза, если признак-фактор x находится в центре области наблюдения x и нельзя ожидать хороших результатов прогноза при удалении xk от x. Если же значение xk оказывается за пределами наблюдаемых значений, используемых при построении линейной регрессии, то результаты прогноза ухудшаются в зависимости от того, насколько xk откланяется от области наблюдаемых значений фактора x.
Однако фактические значения y варьируют около среднего значения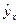 
. Индивидуальные значения y могут отклоняться от 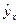на величину случайной ошибки e, дисперсия которой оценивается как остаточная дисперсия на одну степень свободы S. Поэтому ошибка предсказываемого индивидуального значения y должна включать не только стандартную ошибку 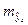, но и случайную ошибку S.
Средняя ошибка прогнозируемого индивидуального значения y составит:
(2.27)
При прогнозировании на основе уравнения регрессии следует помнить, что величина прогноза зависит не только от стандартной ошибки индивидуального значения у, но и от точности прогноза значения фактора x . Его величина может задаваться на основе анализа других моделей исходя из конкретной ситуации, а также анализа динамики данного фактора.
Рассмотренная формула средней ошибки индивидуального значения признака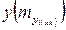 
может быть использована также для оценки существенности различия предсказываемого значения и некоторого гипотетического значения.
№7
Различают два класса нелинейных регрессий:
– регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам;
– регрессии, нелинейные по оцениваемым параметрам.
Примером нелинейной регрессии по включенным в нее объясняющим переменным могут служить следующие функции:
– полиномы разных степеней:
– равносторонняя гипербола
К нелинейным регрессиям по оцениваемым параметрам относятся функции:
– степенная
– показательная
– экспоненциальная
При выборе вида зависимости между двумя признаками нагляден графический метод, особенно для монотонных (не имеющих максимумы и минимумы) зависимостей.
Таблица 2.3. – Основные зависимости и параметры для их выбора
| № | Формула | Xk | Yk | Приведение к линейному виду |
| 1 |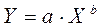 
| 
| 
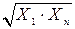
| U = A + bZ; U = lgY; A = lga; Z = lgX |
| 2 | 
| 
| 
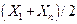
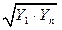
| U = A + BX; U = lgY; A = lga; B = lgb |
| 3 |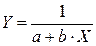 
| 
| 
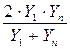
| U = a + bX; U = 1/Y |
| 4 |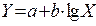 
| 
| 
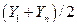
| Y = a + bZ; Z = lgX |
| 5 | 
| 
|
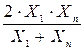
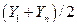
| Y = a + bZ; Z = 1/X |
| 6 | 
|
| 
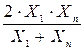
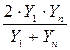
| U = A + BZ; U = 1/Y; Z = 1/X; A = 1/a; B = b/a |
Рассмотрим нелинейные регрессии по оцениваемым параметрам. Пусть в результате наблюдения получен ряд изучаемого показателя X и Y. По этим значениям можно построить график.
| X | x1 | x2 | … | xn |
| Y | y1 | y2 | … | yn |
Теперь необходимо подобрать формулу, которая могла бы описать экспериментальные данные. Для выбора вида зависимости воспользуемся методом средних точек. Для каждой зависимости рассчитываем координаты средних точек Xk и Yk по формулам из таблицы. Средние точки наносим на график и выбираем ту формулу, средняя точка которой лежит ближе всего к экспериментальной кривой.
Затем необходимо определить параметры выбранной зависимости a и b таким образом, чтобы расчетная кривая лежала как можно ближе к экспериментальной кривой. В качестве критерия близости S выбираем минимум суммы квадратов отклонений между экспериментальными и расчетными значениями.
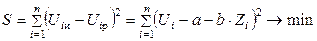. (2.28)
Для каждой формулы в этом критерии будут присутствовать разные переменные в зависимости от приведения их к линейному виду. Например, для первой формулы U = lgY ; Z = lgX. Тогда система нормальных уравнений для определения параметров линейной зависимости будет иметь вид:
,
где [Z] = SZi; [U] = SUi; [Z2] = SZi×Zi; [U×Z] = SUi×Zi; n – количество экспериментов; A = lga и b – искомые коэффициенты уравнения (для определения а необходимо выполнить обратное преобразование: a = 10A).
Для нахождения соответствующих сумм в каждом случае необходимо получить различные вспомогательные таблицы с учетом приведения выражений к линейному виду. Например, для второй формулы иSZi = SXi, а SUi = Slg(Yi) и т.д.
Решив эту систему, получаем искомые значения параметров. Следует отметить, что при нахождении параметров других зависимостей необходимо сначала привести их к линейному виду согласно
Для проверки правильности выполненных действий получаем расчетные значения подстановкой в найденную формулу экспериментальных значений X. Полученные расчетные значения наносим на график с экспериментальными данными и делаем вывод об адекватности.
| X | x1 | x2 | … | xn |
| Y | y1р | y2р | … | ynр |
№8
Парабола второй степени целесообразна к применению, если для определенного интервала значений фактора меняется характер связи рассматриваемых признаков: прямая связь изменяется на обратную или обратная на прямую. В этом случае определяется значение фактора, при котором достигается максимальное (или минимальное) значение результативного признака: приравниваем к нулю первую производную параболы второй степени:
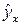= а + b × x + c × x2
т.е. b + 2 × c × x = 0 и x = – b/2c .
Если же исходные данные не обнаруживают изменения направленности связи, то параметры параболы второго порядка становятся трудно интерпретируемыми, а форма связи часто заменяется другими нелинейными моделями.
Применение МНК для оценки параметров параболы второй степени приводит к следующей системе нормальных уравнений:
,
Решить ее относительно параметров а, b , с можно методом определителей:
; 
; 
,
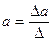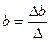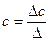где D – определитель системы; D a, D b, D c – частные определители для каждого из параметров.
При b > 0 и с < 0 кривая симметрична относительно высшей точки, т. е. точки перелома кривой, изменяющей направление связи, а именно рост на падение.
Ввиду симметричности кривой параболу второй степени далеко не всегда можно использовать в конкретных исследованиях. Чаще исследователь имеет дело лишь с отдельными сегментами параболы, а не с полной параболической формой. Кроме того, параметры параболической связи не всегда могут быть логически истолкованы. Поэтому если график зависимости не демонстрирует четко выраженной параболы второго порядка (нет смены направленности связи признаков), то она может быть заменена другой нелинейной функцией, например степенной.
Таблица 2.5. Зависимость урожайности озимой пшеницы от количества внесенных удобрений
| Внесено удобрений, ц/га, x | Урожайность, ц/га, y | x2 | x3 | x4 | y × x | y × x2 |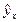 
|
| 1 | 6 | 1 | 1 | 1 | 6 | 6 | 6,2 |
| 2 | 9 | 4 | 8 | 16 | 18 | 36 | 8,5 |
| 3 | 10 | 9 | 27 | 81 | 30 | 90 | 10,4 |
| 4 | 12 | 16 | 64 | 256 | 48 | 192 | 11,9 |
| 5 | 13 | 25 | 125 | 625 | 65 | 325 | 13,0 |
| S = 15 | 50 | 55 | 225 | 979 | 167 | 649 |
система нормальных уравнений составит:
.
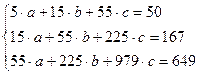Решив эту систему методом определителей, получим:
D = 700, D a = 2380, D b = 2090, D c = – 150.
Откуда параметры искомого уравнения составят: a = 3,4; b = 2,986; c = –0,214, а уравнение параболы примет вид:
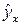= 3,4 + 2,986 × x – 0,214 × x2.
Последовательно подставляя в это уравнение значения x, найдем теоретические значения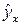
Сумма квадратов отклонений остаточных величин S (y – 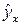)2 = 0,457. Ввиду того, что данные табл.2.4 демонстрируют лишь сегмент параболы второго порядка, рассматриваемая зависимость может быть охарактеризована и другой функцией.
№9
Уравнение нелинейной регрессии, так же как и в линейной зависимости, дополняется показателем корреляции, а именно индексом корреляции (R)
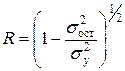(2.29)
где s2ост – остаточная дисперсия, определяемая из уравнения регрессии f(x); s2y – общая дисперсия результативного признака.
Поскольку s2y = (1/n) × S(y – )2, а s2ост = (1/n) × S(y – 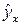)2, индекс корреляции можно выразить как
.
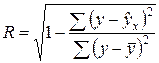Величина данного показателя находится в границах: 0 £ R £ 1; чем ближе к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии.
Разделив остаточную сумму квадратов на соответствующее ей число степеней свободы, получим средний квадрат отклонений или дисперсию на одну степень свободы S2 и вытекающую из нее стандартную ошибку S.
.
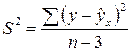
Парабола второй степени, как и полином более высокого порядка, при линеаризации принимает вид уравнения множественной регрессии. Если же нелинейное относительно объясняемой переменной уравнение регрессии при линеаризации принимает форму линейного уравнения парной регрессии, то для оценки тесноты связи может быть использован линейный коэффициент корреляции, величина которого в этом случае совпадает с индексом корреляции ryz, где преобразованная величина признака-фактора, например, z = 1/x или z = ln x.
Приведем в качестве примера равностороннюю гиперболу yx = a + b/x. имеем линейное уравнение yz = a + b × z, для которого может быть определен линейный коэффициент корреляции: b × s z/s y. Возводя данное выражение в квадрат, получим:
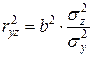, (2.30)
где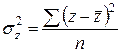 
и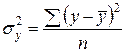 
.
Отсюда r 2 yz можно записать как:
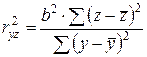. (2.31)
Как было показано в разд.2.3,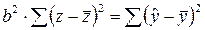 
и соответственно
.
Но так как 
и 
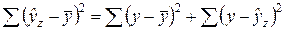, то
,
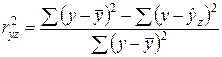т.е. пришли к формуле индекса корреляции:
.
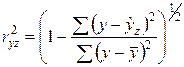Заменив z на 1/x,получим yz = yx, соответственно ryz = Ryx.
Аналогичные выражения можно получить и для полулогарифмической кривой yx = a + b × ln x, ибо в ней, как и в предыдущем случае, преобразования в линейный вид (z = ln x) не затрагивают зависимую переменную, и требование МНК S(y – 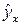)2 ® min выполнимо.
Поскольку в расчете индекса корреляции используется соотношение факторной и общей суммы квадратов отклонений, R2 имеет тот же смысл, что и коэффициент детерминации. В специальных исследованиях величину R2 для нелинейных связей называют индексом детерминации.
Оценка статистической значимости индекса корреляции проводится так же, как и оценка значимости коэффициента корреляции
Индекс детерминации R2 используется для проверки статистической значимости в целом уравнении нелинейной регрессии по F-критерию Фишера.
, (2.35)
где n – число наблюдений; m – число параметров при переменных x.
Величина m характеризует число степеней свободы для факторной суммы квадратов, а (n – m – 1) – число степеней свободы для остаточной суммы квадратов.
. В противном случае проводится оценка существенности различия между R2 и r2, вычисленных по одним и тем же исходным данным, через Стьюдента:
(2.36)
где m!R – r! – ошибка разности между определяемая по формуле
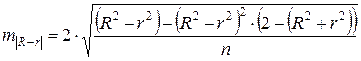(2.37)
Если tфакт > tтабл, то различия между рассматриваемыми показателями корреляции существенны и замена нелинейной регрессии уравнением линейной функции невозможна. Практически если величина t < 2, то различия между R и r несущественны, и, следовательно, возможно применение линейной регрессии, даже если есть предположения о некоторой нелинейности рассматриваемых соотношений признаков фактора и результата.
№10.
Средняя ошибка аппроксимации
Фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии. Чем меньше эти отличия, тем ближе теоретические значения к эмпирическим данным, тем лучше качество модели. Величина отклонений фактических и расчетных значений результативного признака каждому наблюдению представляет собой ошибку аппроксимации. В отдельных случаях ошибка аппроксимации может оказаться равной нулю. Отклонения (y – 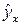) несравнимы между собой, исключая величину, равную нулю. Так, если для одного наблюдения y – 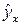= 5, а для другого – 10, то это не означает, что во втором случае модель дает вдвое худший результат. Для сравнения используются величины отклонений, выраженные в процентах к фактическим значениям. Например, если для первого наблюдения y = 20, а для второго y = 50, ошибка аппроксимации составит 25 % для первого наблюдения и 20 % – для второго.
Поскольку (y – 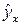) может быть величиной как положительной, так и отрицательной, ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю.
Отклонения (y – 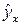) можно рассматривать как абсолютную ошибку аппроксимации, а
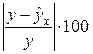
– как относительную ошибку аппроксимации. Для того, чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, находят среднюю ошибку аппроксимации как среднюю арифметическую простую
. (2.38)
По нашим данным представим расчет средней ошибки аппроксимации для уравнения Y = 6,136 × Х0,474 в следующей таблице.
Таблица. Расчет средней ошибки аппроксимации
| y | yx | y –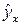
| 
|
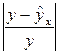
| 6 | 6,135947 | -0,135946847 | 0,022658 |
| 9 | 8,524199 | 0,475801308 | 0,052867 |
| 10 | 10,33165 | -0,331653106 | 0,033165 |
| 12 | 11,84201 | 0,157986835 | 0,013166 |
| 13 | 13,164 | -0,163999272 | 0,012615 |
| Итого | 0,134471 |
A = (0,1345 / 5) × 100 = 2,69 %, что говорит о хорошем качестве уравнения регрессии, ибо ошибка аппроксимации в пределах 5-7 % свидетельствует о хорошем подборе модели к исходным данным.
Возможно и другое определение средней ошибки аппроксимации:
(2.39)
Для нашего примера эта величина составит:
.
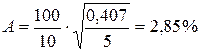Для расчета средней ошибки аппроксимации в стандартных программах чаще используется формула (2.39).
Аналогично определяется средняя ошибка аппроксимации и для уравнения параболы.
№11
Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:
1) быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то нужно придать ему количественную определенность (например, в модели урожайности качество почвы задается в виде баллов; в модели стоимости объектов недвижимости учитывается место нахождения недвижимости: районы могут быть проранжированы);
2) не должны быть коррелированны между собой и тем более находиться в точной функциональной связи.
Включение в модель факторов с высокой интеркорреляцией, когда ryx1 < rx1x2, для зависимости y = a + b1 × x1 + b2 × x2 + e, может привести к нежелательным последствиям – система нормальных уравнений может оказаться плохо обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии.
Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель, и параметры уравнения регрессии оказываются неинтерпретируемыми. Так, в уравнении y = a + b1 × x1 + b2 × x2 + e, предполагается, что факторы x1 и x2 независимы друг от друга, т.е. rx1x2 = 0. Тогда можно говорить, что параметр b1 измеряет силу влияния фактора x1 на результат y при неизменном значении фактора x2. Если же rx1x2 = 1, то с изменением фактора x1 фактор x2 не может оставаться неизменным. Отсюда b1 и b2 нельзя интерпретировать как показатели раздельного влияния x1 и x2 на y.
Пример 3.2. При изучении зависимости y = f(x, z, v) матрица парных коэффициентов корреляции оказалась следующей:
| y | x | z | v | |
| y | 1 | |||
| x | 0,8 | 1 | ||
| z | 0,7 | 0,8 | 1 | |
| v | 0,6 | 0,5 | 0,2 | 1 |
Очевидно, что факторы x и z дублируют друг друга. В анализ целесообразно включить фактор z, а не x, так как корреляция z, с результатом y слабее, чем корреляция фактора x с y (ryz < ryx), но зато слабее межфакторная корреляция rzv < rxv. Поэтому в данном случае в уравнение множественной регрессии включаются факторы z, и v.
По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью, т.е. имеет место совокупное воздействие факторов друг на друга. Наличие мультиколлинеарности факторов может означать, что некоторые факторы всегда будут действовать в унисон. В результате вариация в исходных данных перестает быть полностью независимой и нельзя оценить воздействие каждого фактора в отдельности. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов.
Если рассматривается регрессия y = a + b × x + c × z + d × v + e, то для расчета параметров с применением МНК предполагается равенство
S2y = S2факт + S2e,
где S2y – общая сумма квадратов отклонений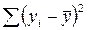 
; S2факт – факторная (объясненная) сумма квадратов отклонений 
; S2e – остаточная сумма квадратов отклонений 
.
В свою очередь, при независимости факторов друг от друга выполнимо равенство
S2факт = S2x + S2z + S2v,
где S2x, S2z, S2v – суммы квадратов отклонений, обусловленные влиянием соответствующих факторов.
Если же факторы интеркоррелированы, то данное равенство нарушается.
Включение в модель мультиколлинеарных факторов нежелательно по следующим причинам:
– затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом» виде, ибо факторы коррелированны; параметры линейной регрессии теряют экономический смысл;
– оценки параметров ненадежны, обнаруживают большие стандартные ошибки и меняются с изменением объема наблюдений (не только по величина, но и по знаку), что делает модель непригодной для анализа и прогнозирования.
Для оценки факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами.
Если бы факторы не коррелировали между собой, то матрицы парных коэффициентов корреляции между ними была бы единичной, поскольку все недиагональные элементы rxixj (xi ¹ xj) были бы равны нулю. Так, для уравнения, включающего три объясняющих переменных,
y = a + b1 × x1 + b2 × x2 + b3 × x3 + e,
матрица коэффициентов корреляции между факторами имела бы определитель, равный единице
,
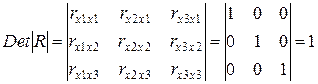поскольку rx 1 x 1 = rx 2 x 2 = rx 3 x 3 = 1 и rx 1 x 2 = rx 1 x 3 = rx 2 x 3 = 0.
Если же между факторами существует полная линейная зависимость и все коэффициенты корреляции равны единице, то определитель такой матрицы равен нулю
.
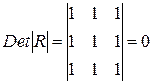Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
Оценка значимости мультиколлинеарности факторов может быть проведена методом испытания гипотезы о независимости переменных H0: DetïRï = 1. Доказано, что величина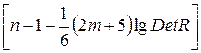 
имеет приближенное распределение c2 с df = m × (m – 1)/2 степенями свободы. Если фактическое значение c2 превосходит табличное (критическое): c2факт > c2табл(df , a) то гипотеза H0 отклоняется. Это означает, что DetïRï ¹ 1, недиагональные ненулевые коэффициенты корреляции указывают на коллинеарность факторов. Мультиколлинеарность считается доказанной.
Через коэффициенты множественной детерминации можно найти переменные, ответственные за мультиколлинеарность факторов. Для этого в качестве зависимой переменной рассматривается каждый из факторов. Чем ближе значение коэффициента множественной детерминации к единице, тем сильна проявляется мультиколлинеарность факторов. Сравнивая между собой коэффициенты множественной детерминации факторов R2x1ïx2x3…xp; R2x2ïx1x3…xp и т.п., можно выделить переменные, ответственные за мультиколлинеарность, следовательно, можно решать проблему отбора факторов, оставляя в уравнении факторы с минимальной величиной коэффициента множественной детерминации.
Имеется ряд подходов преодоления сильной межфакторной корреляции. Самый простой из них состоит в исключении из модели одного или нескольких факторов. Другой путь связан с преобразованием факторов, при котором уменьшается корреляция между ними. Например, при построении модели на основе рядов динамики переходят от первоначальных данных к первым разностям уровней Dy = yt – yt –1, чтобы исключить влияние тенденции, или используются такие методы, которые сводят к нулю межфакторную корреляцию, т.е. переходят от исходных переменных к их линейным комбинациям, не коррелированным друг с другом (метод главных компонент).
Одним из путей учета внутренней корреляции факторов является переход к совмещенным уравнениям регрессии, т.е. к уравнениям, которые отражают не только влияние факторов, но и их взаимодействие. Так, если y = f(x1, x2, x3). то можно построить следующее совмещенное уравнение:
y = a + b1 × x1 + b2 × x2 + b3 × x3 + b12 × x1 × x2 + b13 × x1 × x3 + b23 × x2 × x3 + e.
Рассматриваемое уравнение включает эффект взаимодействия первого порядка. Можно включать в модель и взаимодействие более высоких порядков, если будет доказана его статистическая значимость, например включение взаимодействия второго порядка b123 × x1× x2 × x3 и т.д. Как правила, взаимодействие третьего и более высоких порядков оказывается статистически незначимым; совмещенные уравнения регрессии ограничиваются взаимодействием первого и второго порядков. Но и оно может оказаться несущественным. Тогда нецелесообразно включать в модель взаимодействие всех факторов и всех порядков. Так, если анализ совмещенного уравнения показал значимость только взаимодействия факторов x1×и x3, то уравнение будет иметь вид:
y = a + b1 × x1 + b2 × x2 + b3 × x3 + b13 × x1 × x3 + e.
Взаимодействие факторов x1×и x3 означает, что на разных уровнях фактора x3 влияние фактора x1×на y будет неодинаково, т.е. оно зависит от значений фактора x3. На рис. 3.1 взаимодействие факторов представляется непараллельными линиями связи x1×с результатом y. И, наоборот, параллельные линии влияния фактора x1×на y при разных уровнях фактора x3 означают отсутствие взаимодействия факторов x1×и x3.
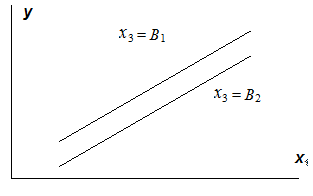
Рис. 3.1. Графическая иллюстрация взаимодействия факторов
Совмещенные уравнения регрессии строятся, например, при исследовании эффекта влияния на урожайность разных видов удобрений (комбинаций азота и фосфора).
Решению проблемы устранения мультиколлинеарности факторов может помочь и переход к уравнениям приведенной формы. С этой целью в уравнение регрессии подставляют рассматриваемый фактор, выраженный из другого уравнения.
Пусть, например, рассматривается двухфакторная регрессия вида yx = a + b1 × x1 + b2 × x2, для которой факторы x1×и x2 обнаруживают высокую корреляцию. Если исключить один из факторов, то мы придем к уравнению парной регрессии. Вместе с тем можно оставить факторы в модели, но исследовать данное двухфакторное уравнение регрессии совместно с другим уравнением, в котором фактор (например, x2) рассматривается как зависимая переменная. Предположим, что x2 = A + B ×y + C × x3. Подставив это уравнение в искомое вместо x2, получим:
yx = a + b1 × x1 + b2 × (A + B × y + C × x3)
или
yx × (1 – b2 × B) = (a + b2 × A) + b1 × x1 + C × b2 × x3.
Если (1 – b2 × B) ¹ 0, то, разделив обе части равенства на (1 – b2 × B), получим уравнение вида
,
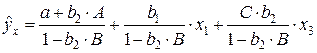которое принято называть приведенной формой уравнения для определения результативного признака y. Это уравнение может быть представлено в виде
yx = a’ + b’1 × x1 + b’3 × x3.
К нему для оценки параметров может быть применен метод наименьших квадратов.
Отбор факторов, включаемых в регрессию, является одним из важнейших этапов практического использования методов регрессии. Подходы к отбору факторов на основе показателей корреляции могут быть разные. Они приводят построение уравнения множественной регрессии соответственно к разным методикам. В зависимости от того, какая методика построения уравнения регрессии принята, меняется алгоритм её решения на компьютере.
Наиболее широкое применение получили следующие методы построения уравнения множественной регрессии:
– метод исключения;
– метод включения;
– шаговый регрессионный анализ.
Каждый из этих методов по-своему решает проблему отбора факторов, давая в целом близкие результаты – отсев факторов из полного его набора (метод исключения), дополнительное введение фактора (метод включения), исключение ранее введенного фактора (шаговый регрессионный анализ).
На первый взгляд может показаться, что матрица парных коэффициентов корреляции играет главную роль в отборе факторов. Вместе с тем вследствие взаимодействия факторов парные коэффициенты корреляции не могут в полной мере решать вопрос о целесообразности включения в модель того или иного фактора. Эту роль выполняют показатели частной корреляции, оценивающие в чистом виде тесноту связи фактора с результатом. Матрица частных коэффициентов корреляции наиболее широко используется в процедуре отсева факторов. Отсев факторов можно проводить и по t-критерию Стьюдента для коэффициентов регрессии: из уравнения исключаются факторы с величиной t-критерия меньше табличного. Так, например, уравнение регрессии составило:
y = 25 + 5x1 + 3x2 + 4x3 + e.
(4,0) (1,3) (6,0)
В скобках приведены фактические значения t-критерия для соответствующих коэффициентов регрессии, как правило, при t < 2 коэффициент регрессии незначим и, следовательно, рассматриваемый фактор не должен присутствовать в регрессионной модели. В данном случае – это фактор x2.
При отборе факторов рекомендуется пользоваться следующим правилом: число включаемых факторов обычно в 6-7 раз меньше объема совокупности, по которой строится регрессия. Если это соотношение нарушено, то число степеней свободы остаточной вариации очень мало. Это приводит к тому, что параметры уравнения регрессии оказываются статистически незначимыми, а F-критерий меньше табличного значения.
Выбор формы уравнения регрессии
Как и в парной зависимости, используются разные виды уравнений множественной регрессии: линейные и нелинейные.
Ввиду четкой интерпретации параметров наиболее широко используются линейная и степенная функция. В линейной множественной регрессии y = a + b1 × x1 + b2 × x2 + … + bp × xp параметры при x называются коэффициентами «чистой» регрессии. Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизменном значении других факторов, закрепленных на среднем уровне.
Пример 3.3. Предположим, что зависимость расходов на продукты питания по совокупности семей характеризуется следующим уравнением:
y = 0,5 + 0,35x1 + 0,73x2,
где y –расходы семьи за месяц на продукты питания, тыс. руб.; x1 – месячный доход на одного члена семьи, тыс. руб.; x2 – размер семьи, человек.
Анализ данного уравнения позволяет сделать выводы – с ростом дохода на одного члена семьи на 1 тыс. руб. расходы на питание возрастут в среднем на 350 руб. при том же среднем размере семьи. Иными словами, 35 % дополнительных семейных расходов тратится на питание. Увеличение размера семьи при тех же её доходах предполагает дополнительный рост расходов на питание на 730 руб. Параметр a не имеет экономической интерпретации.
При изучении вопросов потребления коэффициенты регрессии рассматриваются как характеристики предельной склонности в потреблению. Например, если функция потребления Ct имеет вид
Ct = a + b0 × Rt + b1 × Rt–1 + e,
то потребление в период времени t зависит от дохода того же периода Rt и от дохода предшествующего периода Rt–1. Соответственно коэффициент b0 характеризует эффект единичного возрастания дохода Rt при неизменном уровне предыдущего дохода. Коэффициент b0 обычно называют краткосрочной предельной склонностью к потреблению. Общим эффектом возрастания как текущего, так и предыдущего дохода будет рост потребления на b = b1. Коэффициент b рассматривается здесь как долгосрочная склонность к потреблению. Поскольку коэффициенты b0 и b1 > 0, долгосрочная склонность к потреблению должна превосходить краткосрочную b0. Напрмер, за период 1905-1951 гг. (за исключением военных лет) М.Фридман построил для США следующую функцию потребления: Ct = 53 + 0,58 × Rt + 0,32 × Rt–1 с краткосрочной предельной склонностью к потреблению 0,58 и с долгосрочной склонностью к потреблению 0,9.
Функция потребления может рассматриваться также в зависимости от прошлых привычек потребления, т.е. от предыдущего уровня потребления Ct –1:
Ct = a + b0 × Rt + b1 × Ct–1 + e.
В этом уравнении параметр b0 также характеризует краткосрочную предельную склонность к потреблению, т.е. влияние на потребление единичного роста доходов того же периода Rt. Долгосрочную предельную склонность к потреблению здесь измеряет выражение b0/(1 – b1).
Так, если уравнение регрессии составило:
Ct = 23,4 + 0,46 × Rt + 0,20 × Ct–1 + e.
то краткосрочная склонность к потреблению равна 0,46, а долгосрочная – 0,575 (0,46/0,8).
Свободный член уравнения множественной линейной регрессии (параметр a) вбирает в себя информацию о прочих не учитываемых в модели факторах. Его величина экономической интерпретации не имеет. Формально его значение предполагает то значение y, когда все x = 0, что практически не бывает.
В степенной функции yx = a × x1b1 ×x2b2 × … ×xpbp коэффициенты bj являются коэффициентами эластичности. Они показывают, на сколько процентов в среднем изменяется результат с изменением соответствующего фактора на 1 % при неизменности действия других факторов. Этот вид уравнения регрессии получил наибольшее распространение в производственных функциях, в исследованиях спроса и потребления.
Предположим, что при исследовании спроса на мясо получено уравнение
yx = 0,82 × x1–2,63 × x21,11 ×или yx = 0,82 × x21,11/x12,63,
где yx – количество спрашиваемого мяса; x1 – цена; x2 – доход.
Следовательно, рост цен на 1 % при том же доходе вызывает снижение спроса в среднем на 2,63 %. Увеличение дохода на 1 % обусловливает при неизменных ценах рост спроса на 1,11 %.
В производственных функциях вида
P = a × F1b1 × F2b2 … × Fmbm × e,
где P – количество продукта, изготавливаемого с помощью m производственных факторов (F1, F2, … Fm); b – параметр, являющийся эластичностью количества продукции по отношению к количеству соответствующих производственных факторов.
Экономический смысл имеют не только коэффициенты b каждого фактора, но и их сумма, т.е. сумма эластичности: B = b1 + b2 + … + bm. Эта величина фиксирует обобщенную характеристику эластичности производства. Пусть производственная функция имеет вид:
P = 2 × F10,3 × F20,2 × F30,5 × e,
где P – выпуск продукции; F1 – стоимость основных производственных фондов; F2 – отработано человеко-дней; F3 – затраты на производство.
Эластичность выпуска по отдельным факторам производства составляет в среднем 0,3 % с ростом F1 на 1 % при неизменном уровне других факторов; 0,2 % – с ростом F2 на 1 % также при неизменности других факторов производства; 0,5 % – с ростом F3 на 1 % при неизменном уровне других факторов. Для данного уравнения B = b1 + b2 + b 3 = 1. Следовательно в целом с ростом каждого фактора производства на 1 % коэффициент эластичности выпуска продукции составляет 1 %, т.е. выпуск продукции увеличивается на 1 %, что в микроэкономике соответствует постоянной отдаче от масштаба.
При практических расчетах не всегда сумма коэффициентов равна единице. Она может быть как больше, так и меньше единицы. В этом случае величина B фиксирует приближенную оценку эластичности выпуска с ростом каждого фактора производства на 1 % в условиях увеличивающейся (B > 1) или уменьшающейся (B < 1) отдачи от масштаба.
Так, если P = 2,4 × F10,3 × F20,7 × F30,2, то с ростом значений каждого фактора производства на 1 % выпуск продукции в целом возрастает приблизительно на 1,2 %.
Возможны и другие линеаризуемые функции для построения уравнения множественной регрессии:
– экспонента 
;
– гипербола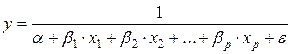 
, которая используется при обратных связях признаков.
Стандартные компьютерные программы обработки регрессионного анализа позволяют перебирать различные функции и выбрать ту из них, для которой остаточная дисперсия и ошибка аппроксимации минимальны, а коэффициент детерминации максимален.
Если исследователя не устраивает предлагаемый стандартной программой набор функций регрессии, то можно использовать любые другие функции, приводимые путем соответствующих преобразований к линейному виду, например
.
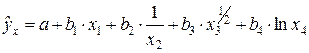Обозначив
z1 = x1, z2 = 1/x2, z3 = x31/2, z4 = ln x4,
получим линейное уравнение множественной регрессии
y = a + b1 × z1 + b2 × z2 + b3 × z3 + b4 × z4 + e.
Однако чем сложнее функция, тем менее интерпретируемы её параметры.
При использовании сложных полиномиальных функций с большим числом факторов необходимо помнить, что каждый параметр преобразованной функции является средней величиной, которая должна быть подсчитана по достаточному числу наблюдений. Если число наблюдений невелико, что, как правило, имеет место в эконометрике, то увеличение числа параметров функции приведет к их статистической незначимости и соответственно потребует упрощения вида функции. Если один и тот же фактор вводится в регрессию в разных степенях, то каждая степень рассматривается как самостоятельный фактор. Так, если модель имеет вид полинома второго порядка
y = a + b1 × x1 + b2 × x2 + b11 × x12 + b22 × x22 + b12 × x1 × x2 + e,
то после замены переменных z1 = x1, z2 = x2, z3 = x12, z4 = x22, z5 = x1x2, получим линейное уравнение регрессии с пятью факторами
y = a + b1 × z1 + b2 × z2 + b3 × z3 + b4 × z4 + b5 × z5 + e.
Поскольку, как отмечалось, должно выполняться соотношение между числом параметров и числом наблюдений, для полинома второй степени требуется не менее 30-35 наблюдений.
В эконометрике регрессионные модели часто строятся на основе макроуровня экономических показателей, когда ставится задача оценки влияния наиболее экономически существенных факторов на моделируемый показатель при ограниченном объеме информации. Поэтому полиномиальные модели высоких порядков используются редко.
К линейному виду может быть приведена и следующая экспоненциальная модель: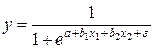 
, так как 
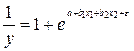или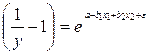 
. Далее, логарифмируя обе части равенства, получим: 
, где 
можно обозначить через Y, т.е. имеем линейную модель множественной регрессии Y = a + b1 × x1 + b2 × x2 + e .
№12
Оценка параметров
Параметры уравнения множественной регрессии оцениваются, как и в парной регрессии, методом наименьших квадратов. При его применении строится система, решение которой и позволяет получить оценки параметров регрессии.
Так, для уравнения y = a + b1 × x1 + b2 × x2 + … + bp × xp +e система нормальных уравнений составит:
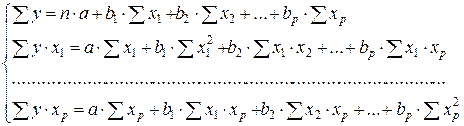
Её решение может быть осуществлено методом определителей:
a = D a / D, b1 = D b1 / D,…, bp = D bp / D,
где D – определитель системы; D a, D b1, …, D bp – частные определители.
При этом
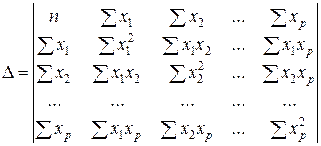
а D a, D b1, …, D bp получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы.
Процедура оценки параметров b0 = a, b1, b2, bk та же, что и в парной линейной регрессии, т.е. находим по правилу умножения матрицу XTX, обратную матрицу (XTX)–1, XTY, и далее оценки B, как: B = (XTX)–1XTY.
Пример 3.4. Имеются следующие данные по 10 предприятиям концерна о прибыли (y – млн. руб.), выработке продукции на одного работника (x1 – единиц) и доле продукции, производимой на экспорт (– %), приведенные в табл. 3.1.
Таблица 3.1. Исходные и расчетные данные для примера построения множественной регрессии
| № п/п | y | x1 | x2 | y2 | x12 | x22 | yx1 | yx2 | x1x2 | yr |
| 1 | 2 | 11 | 3 | 4 | 121 | 9 | 22 | 6 | 33 | 2,284553 |
| 2 | 1 | 10 | 2 | 1 | 100 | 4 | 10 | 2 | 20 | 1,45935 |
| 3 | 3 | 12 | 4 | 9 | 144 | 16 | 36 | 12 | 48 | 3,109756 |
| 4 | 8 | 18 | 10 | 64 | 324 | 100 | 144 | 80 | 180 | 8,060976 |
| 5 | 7 | 15 | 11 | 49 | 225 | 121 | 105 | 77 | 165 | 6,544715 |
| 6 | 5 | 13 | 6 | 25 | 169 | 36 | 65 | 30 | 78 | 4,174797 |
| 7 | 4 | 13 | 5 | 16 | 169 | 25 | 52 | 20 | 65 | 3,934959 |
| 8 | 6 | 15 | 7 | 36 | 225 | 49 | 90 | 42 | 105 | 5,585366 |
| 9 | 7 | 16 | 10 | 49 | 256 | 100 | 112 | 70 | 160 | 6,890244 |
| 10 | 7 | 17 | 12 | 49 | 289 | 144 | 119 | 84 | 204 | 7,955285 |
| Итого | 50 | 140 | 70 | 302 | 2022 | 604 | 755 | 423 | 1058 |
Система нормальных уравнений составит:
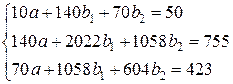
Решая ее методом определителей, получим:
D = 9840, D a = –47960, D b1 = 5760, D b2 = 2360,
откуда:
a = –4,874; b1 = 0,585; b2 = 0,240.
Уравнение регрессии выглядит следующим образом:
№13
На основе линейного уравнения множественной регрессии
y = a + b1 × x1 + b2 × x2 + … + bp × xp + e
могут быть найдены частные уравнения регрессии:
т.е. уравнения регрессии, которые связывают результативный признак с соответствующими факторами x при закреплении других учитываемых во множественной регрессии факторов на среднем уровне. Частные уравнения регрессии имеют следующий вид:
;
;
.
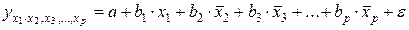При подстановке в эти уравнения средних значений соответствующих факторов они принимают вид парных уравнений линейной регрессии, т.е. имеем:
;
;
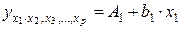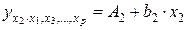где
;
;
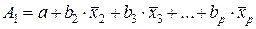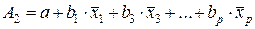В отличие от парной регрессии частные уравнения регрессии характеризуют изолированное влияние фактора на результат, ибо другие факторы закреплены на неизменном уровне. Эффекты влияния других факторов присоединены в них к свободному члену уравнения множественной регрессии. Это позволяет на основе частных уравнений регрессии определять частные коэффициенты эластичности:
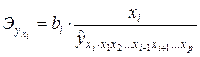(3.5)
где bi – коэффициенты регрессии для фактора xi в уравнении множественной регрессии;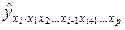 
– частное уравнение регрессии.
Пример 3.7. Предположим, что по ряду регионов множественная регрессия величины импорта на определенный товар y относительно отечественного его производства x1, изменения запасов x2 и потребления на внутреннем рынке x3 оказалась следующей:
y = –66,028 + 0,135 × x1 + 0,476 × x2 + 0,343 × x3.
При этом средние значения для рассматриваемых признаков составили:
y = 31,5; x1 =245; x2 =3,7; x3 = 12,5.
На основе данной информации могут быть найдены средние по совокупности показатели эластичности:
.
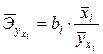Для этого примера они окажутся равными:
,
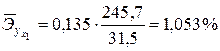т.е. с ростом объема отечественного производства на 1 % размер импорта в среднем по совокупности регионов возрастет на 1,053 % при неизменных запасах и потреблении семей.
Для второй переменной коэффициент эластичности составляет:
,
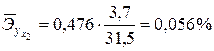т.е. с ростом изменения запасов на 1 % при неизменном производстве и внутреннем потреблении величина импорта увеличивается в среднем на 0,056 5.
Для третьей переменной коэффициент эластичности составляет:
,
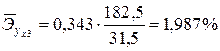т.е. при неизменном объеме производства и величины запасов с увеличением внутреннего потребления на 1 % импорт товара возрастает в среднем на 1,987 %. Средние показатели эластичности можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат. В рассматриваемом примере наибольшее воздействие на величину импорта оказывает размер внутреннего потребления товара x3, а наименьшее – изменение запасов x2.
Наряду со средними показателями эластичности в целом по совокупности регионов на основе частных уравнений регрессии могут быть определены частные коэффициенты эластичности для каждого региона.
Частные уравнения регрессии в нашем случае составят:
,
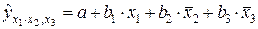т.е.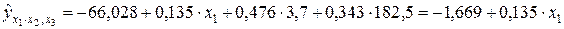 
;
,
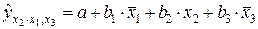т.е.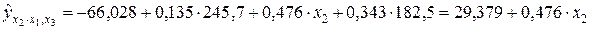 
;
,
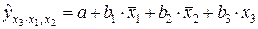т.е.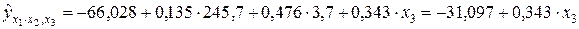 
.
Подставив в данные уравнения фактические значения соответствующих факторов по отдельным регионам, получим значения моделируемого показателя y при заданном уровне одного фактора и средних значениях других факторов. Эти расчетные значения результативного признака используются для определения частных коэффициентов эластичности по приведенной выше формуле. Так, если в регионе x1 = 160,2; x2 = 4,0; x3 = 190,5, то частные коэффициенты эластичности составят:
;
;
.
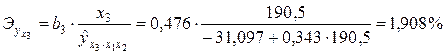Как видим, частные коэффициенты эластичности для региона несколько отличаются от аналогичных средних показателей по совокупности регионов. Они могут быть использованы при принятии решений по развитию конкретных регионов.
№14.
Множественная корреляция
Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком, или оценивает тесноту совместного влияния факторов на результат.
Независимо от формы связи показатель множественной корреляции может быть найден как индекс множественной корреляции:
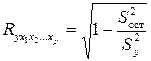
где S2ост – остаточная сумма квадратов для уравнения y = f(x1, x2,…,xp); S2y – общая сумма квадратов результативного признака.
Чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов.
Можно пользоваться следующей формулой индекса множественной корреляции
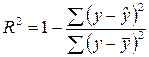. (3.7)
(3.8)
Формула индекса множественной корреляции для линейной регрессии получила название линейного коэффициента множественной корреляции или совокупного коэффициента корреляции.
Найдем для нашего примера совокупный коэффициент корреляции:
.
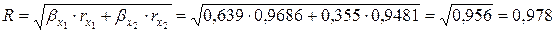Для того чтобы не допустить возможного преувеличения тесноты связи, применяется скорректированный индекс (коэффициент) множественной корреляции
Скорректированный индекс множественной корреляции содержит поправку на число степеней свободы, а именно остаточная сумма квадратов 
делится на число степеней свободы остаточной вариации (п – т – 1), а общая сумма квадратов отклонений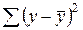 
– на число степеней свободы в целом по совокупности (п – 1).
Формула скорректированного индекса множественной детерминации имеет вид:
, (3.17)
где п – число наблюдений; т – число параметров при переменных
. (3.18)
Чем больше величина т, тем сильнее различия 
и R2.
Для линейной зависимости признаков скорректированный коэффициент множественной корреляции определяется по той же формуле, что и индекс множественной корреляции, Т.е. как корень квадратный из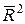 
. Отличие состоит лишь в том, что в линейной зависимости под т подразумевается число факторов, включенных в регрессионную модель, а в криволинейной зависимости т – число параметров при х и их преобразованиях ( x2, ln х и др.), которое может быть больше числа факторов как экономических переменных.
ЧАСТНАЯ КОРРЕЛЯЦИЯ
Частные коэффициенты (или индексы) корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии.
Показатели частной корреляции представляют собой отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в модель.
Предположим, что зависимость y x1 характеризуется уравнением
yx1 = a + b1 × x1.
Подставив в это уравнение фактическое значение x1, найдем теоретические величины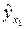 
и соответствующую величину остаточной дисперсии s2:
.
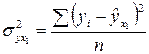Включив в уравнение регрессии дополнительный фактор x2, получим уравнение регрессии вида
yx1x2 = a + b1 × x1 + b2 × x2.
Чем большее число факторов включено в модель, тем меньше величина остаточной дисперсии, т.е. происходит ее сокращение. Чем больше доля этого сокращения в остаточной вариации до введения дополнительного фактора, тем теснее связь между y и x2 при постоянном действии фактора x1. Следовательно, чистое влияние фактора x2 на результат y можно найти как
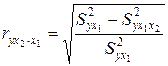. (3.19)
Знак «точка» в выражении частного коэффициента корреляции ryx2×x1 означает элиминирование той переменной (переменных), которая стоит после знака «точка».
Аналогично определяется и чистое влияние на результат y фактора x1:
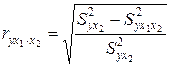. (3.20)
Если выразить остаточную дисперсию через показатель детерминации S2ост = S2y (1 – r2), то формула коэффициента частной корреляции примет вид:
. (3.21)
Соответственно
.
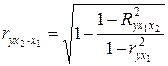Рассмотренные показатели частной корреляции принято называть коэффициентами (индексами) частной корреляции первого порядка, ибо они фиксируют тесноту связи двух переменных при закреплении (элиминировании влияния) одного фактора.
Если рассматривается регрессия с числом факторов р, то возможны частные коэффициенты корреляции не только первого, но и второго, третьего, ..., (р – 1) порядка, т. е. влияние фактора x1 можно оценить при разных условиях независимости действия других факторов:
ryx1×x2 – при постоянном действии фактора x2;
ryx1×x2x3 – при постоянном действии факторов x2 и x3;
ryx1×x2…xp – при неизменном действии всех факторов, включенных в уравнение регрессии.
Сопоставление коэффициентов частной корреляции разных порядков по мере увеличения числа включаемых факторов показывает процесс «очищения» связи результативного признака с исследуемым фактором.
Хотя частная корреляция разных порядков и может представлять аналитический интерес, в практических исследованиях предпочтение отдают показателям частной корреляции самого высокого порядка, ибо именно эти показатели являются дополнением к уравнению множественной регрессии.
В общем виде при наличии р факторов для уравнения
y = a + b1 × x1 + b2 × x2 + … + bp × xp + e.
коэффициент частной корреляции, измеряющий влияние на у фактора xi; при неизменном уровне других факторов, можно определить по формуле
. (3.23)
где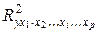 
– множественный коэффициент детерминации всего комплекса р факторов с результатом; 
– тот же показатель детерминации, но без введения в модель фактора xi.
При i = 1 формула коэффициента частной корреляции примет вид:
. (3.24)
Данный коэффициент частной корреляции позволяет измерить тесноту связи между у и xi при неизменном уровне всех других факторов, включенных в уравнение регрессии.
Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается. Например, ryx1×x2 – коэффициент частной корреляции первого порядка. Соответственно коэффициенты парной корреляции называются коэффициентами нулевого порядка. Коэффициенты частной корреляции более высоких порядков можно найти через коэффициенты частной корреляции более низких порядков по рекуррентной формуле
. (3.25)
При двух факторах и i = 1 данная формула примет вид:
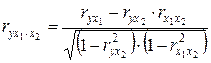. (3.26)
Соответственно при i = 2 и двух факторах частный коэффициент корреляции у с фактором x2 можно определить по формуле
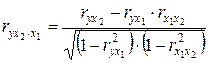. (3.27)
В основном их используют на стадии формирования модели, в частности в процедуре отсева факторов.
Зная частные коэффициенты корреляции (последовательно первого, второго и более высокого порядка), можно определить совокупный коэффициент корреляции по формуле
. (3.31)
При полной зависимости результативного признака от исследуемых факторов коэффициент совокупного влияния их равен единице. Из единицы вычитается доля остаточной вариации признак (1 – r2), обусловленная последовательно включенными в анализ факторами. В результате подкоренное выражение характеризует совокупное действие всех исследуемых факторов.
№15
Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью F-критерия Фишера:
где s2факт – факторная дисперсия на одну степень свободы; R2 – коэффициент (индекс) множественной детерминации; n – число наблюдений; m – число параметров при переменных x (в линейной регрессии совпадает с числом включенных в модель факторов); s2ост – остаточная дисперсия на одну степень свободы.
Определяем все суммы квадратов и дисперсии. Общая сумма квадратов:
.
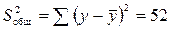Остаточная сумма квадратов:
.
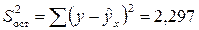Факторная:
.
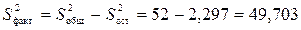Факторная дисперсия на одну степень свободы
.
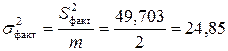Остаточная дисперсия на одну степень свободы s2ост и вытекающую из нее стандартную ошибку s:
.
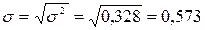Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F-отношения, т.е. критерий F:
.
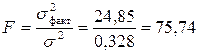Или по формуле (3.32):
.
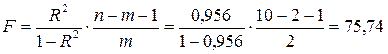Оценивается значимость не только уравнения в целом, но и фактора, дополнительно включенного в регрессионную модель. Необходимость такой оценки связана с тем, что не каждый фактор, вошедший в модель, может существенно увеличивать долю объясненной вариации результативного признака. Кроме того, при наличии в модели нескольких факторов они могут вводиться в модель в разной последовательности. Ввиду корреляции между факторами значимость одного и то го же фактора может быть разной в зависимости от последовательности введения в модель. Мерой для оценки включения фактора в модель служит частный F-критерий, т.е. Fxi.
С помощью частного F-критерия можно проверить значимость всех коэффициентов регрессии в предположении, что каждый соответствующий фактор xi был введен в уравнение множественной регрессии последним.
Для проверки значимости коэффициентов регрессии определяется средняя квадратическая ошибка каждого коэффициента регрессии по формуле:
.
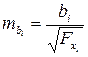Затем определяется значение t-критерия Стьюдента по известной формуле:
.
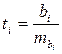Если величина частного F-критерия выше табличного значения, то это означает одновременно не только значимость рассматриваемого коэффициента регрессии, но и значимость частного коэффициента корреляции. Существует взаимосвязь между квадратом частного коэффициента корреляции и частным F-критерием, а именно
, (3.41)
где r2yxi×x1…xi–1xi+1…xp – частный коэффициент детерминации фактора xi с y при неизменном уровне всех других факторов; 1 – R2yx1…xi–1xi+1…xp – доля остаточной вариации уравнения регрессии, включающего все факторы, кроме фактора xi; 1 – R2yx1…xp – доля остаточной вариации для уравнения регрессии с полным набором факторов.
Взаимосвязь показателей частного коэффициента корреляции, частного F-критерия и t-критерия Стьюдента для коэффициентов чистой регрессии может использоваться в процедуре отбора факторов. Отбор факторов при построении уравнения регрессии методом исключения практически можно осуществлять не только по частным коэффициентам корреляции, исключая на каждом шаге фактор с наименьшим незначимым значением частного коэффициента корреляции, но и по величинам tbi и Fxi. Частный F-критерий широко используется и при построении модели методом включения переменных и шаговым регрессионным методом.
№16
нелинейному уравнению множественной регрессии, в качестве которого выбираем полный полином второго порядка:
Для определения коэффициентов такого уравнения средствами Excel необходимо дополнительно сформировать 6 столбцов для расчета коэффициентов от b11 до b23. После этого применяем процедуру Регрессия \ Анализ данных. Результаты в следующей таблице:
Расчетные значения по этому уравнению приведены в соответствующем столбце таблицы. Статистические характеристики. Общая сумма квадратов:
.
Остаточная сумма квадратов:
.
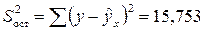Факторная:
.
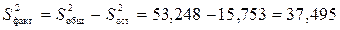Факторная дисперсия на одну степень свободы sфакт = 37,495/9 = 4,166. Остаточная дисперсия на одну степень свободы s2ост и вытекающая из нее стандартная ошибка sост:
.
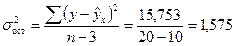
Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F-отношения, т.е. критерий F:
.
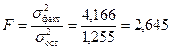Индекс множественной корреляции:
.
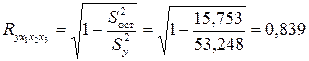Коэффициент детерминации:
.
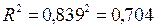Критерий Фишера по формуле (3.32):
.
Величина скорректированного индекса детерминации
.
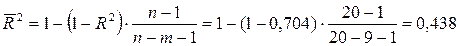Средняя ошибка аппроксимации A = (17,62 / 20) × 100 = 88,11 %. Или:
.
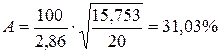Для полученных уравнений 1-го и 2-го порядков можно подсчитать все статистические характеристики, как в примере для линейной множественной регрессии: частный F-критерий, ошибки в определении коэффициентов и значения критериев Стьюдента для каждого из них, уравнение регрессии в стандартизованном масштабе и его статистические характеристики.
Дата добавления: 2021-03-18; просмотров: 75; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!