Координаты правильной шестиугольной призмы
Шестиугольная призма — это «клонированная» трехгранная. Можно понять, как это происходит, если взглянуть на нижнее основание — обозначим его ABCDEF. Проведем дополнительные построения: отрезки AD, BE и CF. Получилось шесть треугольников, каждый из которых (например, треугольник ABO) является основанием для трехгранной призмы.

Теперь введем систему координат. Начало координат — точку O — поместим в центр симметрии шестиугольника ABCDEF. Ось x пойдет вдоль FC, а ось y — через середины отрезков AB и DE. Получим такую картинку:
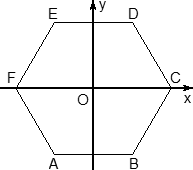
Нужно обратить внимание на то, что начало координат не совпадает с вершиной многогранника. На самом деле, при решении настоящих задач выясняется, что это очень удобно, поскольку позволяет значительно уменьшить объем вычислений. Осталось добавить ось z. Проводим ее перпендикулярно плоскости OXY и направляем вертикально вверх. Получим картинку:
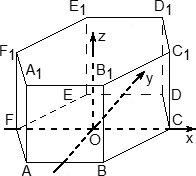
Запишем теперь координаты точек. Предположим, что все ребра нашей правильной шестигранной призмы равны 1. Итак, координаты нижнего основания:
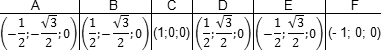
Координаты верхнего основания сдвинуты на единицу по оси z:
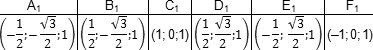
Координаты правильной четырехугольной пирамиды
Итак, правильная четырехугольная пирамида. Обозначим ее SABCD, где S — вершина. Введем систему координат: начало в точке A, единичный отрезок AB = 1, ось x направим вдоль AB, ось y — вдоль AD, а ось z — вверх, перпендикулярно плоскости OXY. Для дальнейших вычислений нам потребуется высота SH — вот и построим ее. Получим следующую картинку:
|
|
|
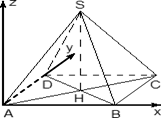
Теперь найдем координаты точек. Для начала рассмотрим плоскость OXY. Здесь все просто: в основании лежит квадрат, его координаты известны. Проблемы возникают с точкой S. Поскольку SH — высота к плоскости OXY, точки S и H отличаются лишь координатой z. Длина отрезка SH — это и есть координата z для точки S, поскольку H = (0,5; 0,5; 0).
Заметим, что треугольники ABC и ASC равны по трем сторонам (AS = CS = AB = CB = 1, а сторона AC — общая). Следовательно, SH = BH. Но BH — половина диагонали квадрата ABCD, т.е. BH = AB · sin 45°. Получаем координаты всех точек:




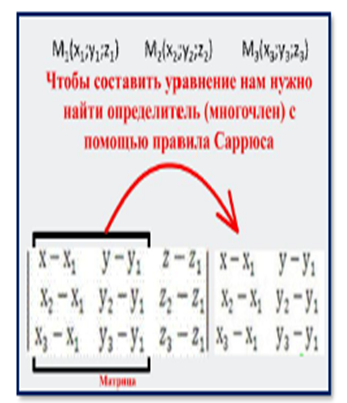
Ниже представлено, как найти определитель третьего порядка по правилу Саррюса, составить уравнение плоскости и найти вектор нормали.

Практическая часть
Ниже представлены задачи:
- на нахождение угла между прямыми;
- угла между прямой и плоскостью;
- угла между плоскостями;
- расстояния от точки до прямой;
- расстояния от точки до плоскости.
Эти задачи решили мои ученики 11 класса
Вариант 13. Задача №14 по сборнику Ф.Ф.Лысенко
В кубе ABCDA1B1C1D1, ребро которого равно 4, точка М является серединой отрезка BC1. Найдите расстояние между прямыми А1В и АМ.
|
|
|



Задача №14 по сборнику ФИПИ 2016
В правильной шестиугольной призме ABCDEFA1B1C1D1 E1F1 все рёбра равны 1. Найдите расстояние от точки В до прямой C1F.

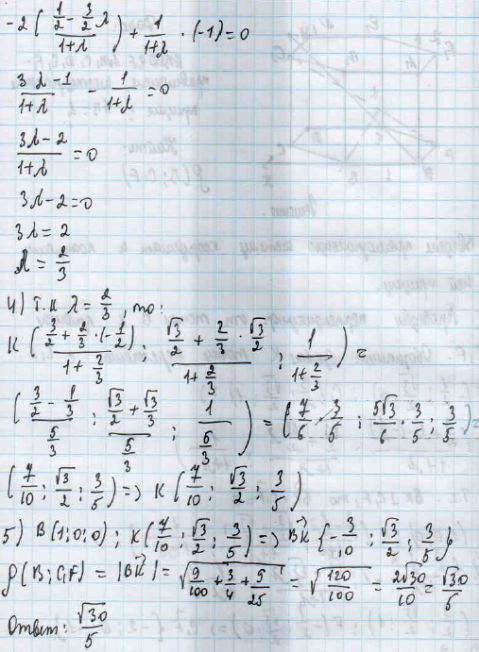
Задача №14 по сборнику ФИПИ 2017
Дана правильная четырёхугольная призма ABCDA1B1C1D1. Найдите расстояние от точки B1 до плоскости AD1 C , если АВ равно 5, АА1равно 6.


Задача №14 ЕГЭ по сборнику ФИПИ 2017
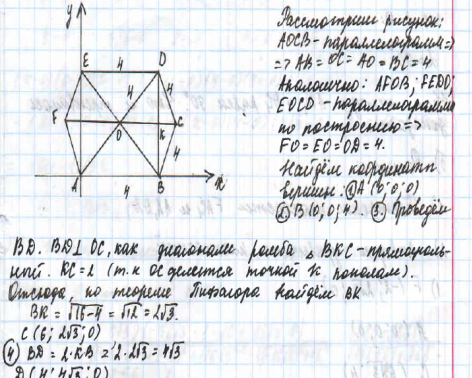
В правильной шестиугольной призме ABCDEFA1B1C1D1 E1F1 все рёбра равны 4.
а) Докажите, что угол между прямыми АD1 и DC1 равен 900.
б) Найдите угол между плоскостями FAC1 и AA1D.




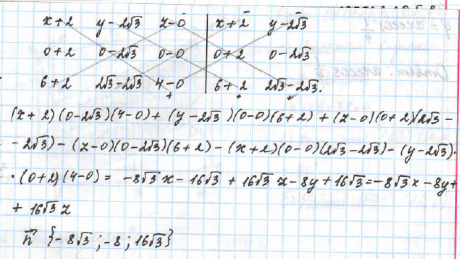
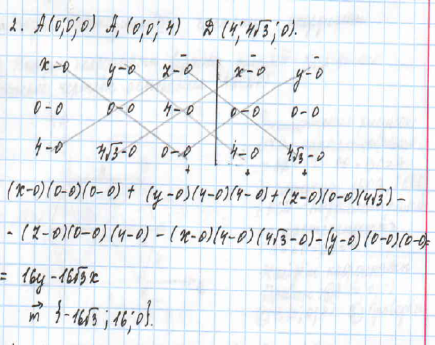
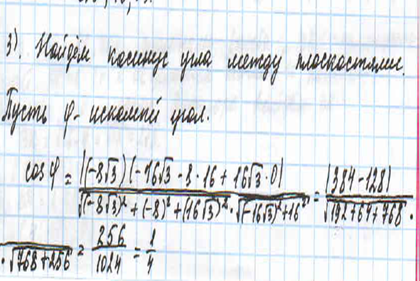

Задача №14 ЕГЭ по сборнику ФИПИ 2017
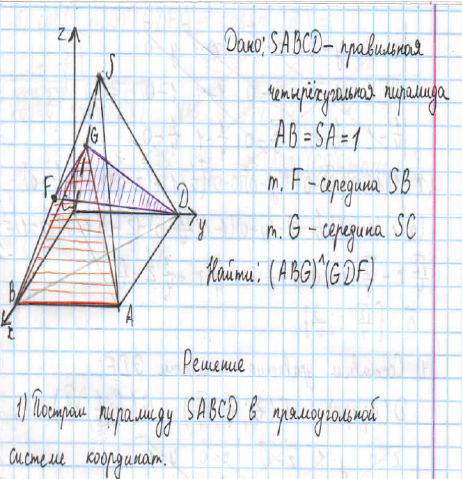


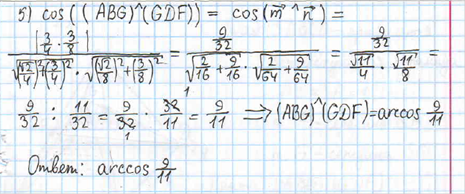


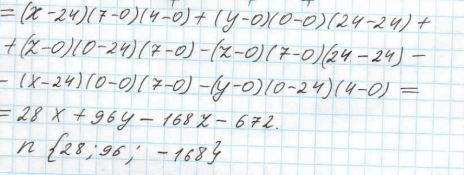
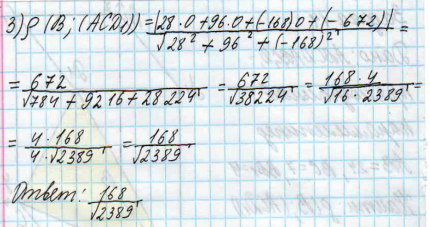
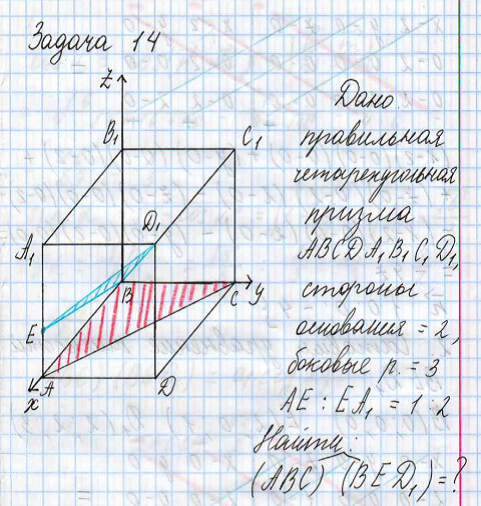
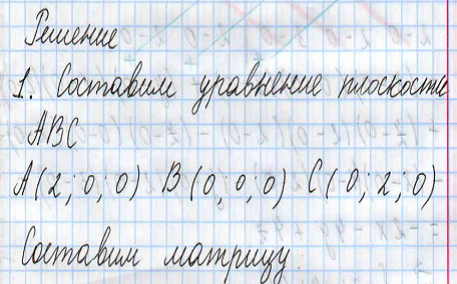

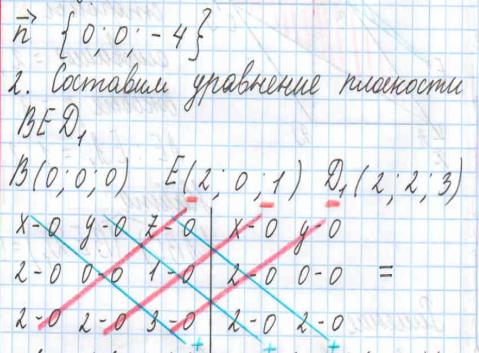
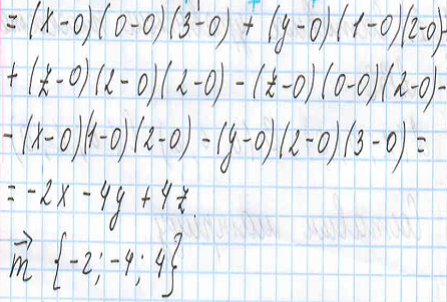

Вывод
Мы изучили метод координат на более высоком уровне по сравнению со школьной программой по геометрии. Познакомились и научились применять новые формулы: на нахождение расстояния от точки до плоскости, от точки до прямой, угла между прямыми, угла между прямой и плоскостью, угла между плоскостями. Мы узнали, что для составления уравнения плоскости можно использовать матрицу и определитель третьего порядка, который можно посчитать правилом Саррюса.
Мы пришли к выводу, что использование метода координат требует от ученика внимательности, хороших вычислительных навыков. Мы убеждены в том, что координатно-векторный метод в школьном курсе геометрии необходимо изучать на глубоком уровне и увеличить количество часов на изучение данной темы.
|
|
|
Нами подобраны задания из сборников ФИПИ 2016г и 2017г, которые мы самостоятельно решили и которые помогут отработать полученные навыки, и тем самым более качественно подготовиться к сдаче экзамена.
Мы надеемся, что изложенная в работе информация поможет выпускникам решать задание №14 и достичь более высоких результатов на ЕГЭ по математике
Список литературы
1. ЕГЭ 2017. Математика. И.В. Ященко. 36 вариантов. Профильный уровень
2. ru.wikipedia.org – Система координат.
3. Смирнова, И.М. C50 Геометрия. Расстояния и углы в пространстве: учебно-методическое пособие / И.М. Смирнова, В.А. Смирнов. – 2-е изд., перераб. И доп. – М.: Издательство «Экзамен», 2009. – 158, [2] с. (Серия «ЕГЭ. 100 баллов»)
4. Геометрия, 10 – 11 : Учеб. Для общеобразоват. учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 13-е изд. – М.: Просвещение, 2014. – 206 с.: ил.
5. Корянов А.Г, Прокофьев А.А. Многогранники: виды задач и методы их решения. МАТЕМАТИКА ЕГЭ 2013 (типовые задания С2) «Многогранники: виды задач и методы их решения» www.alexlarin.narod.ru
|
|
|
6. Корянов А.Г, « Расстояния и углы в пространстве» МАТЕМАТИКА ЕГЭ 2010 (типовые задания С2) www.alexlarin.narod.ru
7. В.В. Леваков «Решение задач координатно-векторным методом»
Дата добавления: 2021-03-18; просмотров: 471; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
