Описание лабораторной установки
Лабораторная работа №4. «Исследование переходных процессов в линейных электрических цепях ВТОРОГО порядка»
Цель работы: снятие переходных и импульсных характеристик простейших электрических цепей и сопоставление результатов эксперимента с результатами расчета.2.1. Краткие теоретические сведения
Краткие теоретические сведения
В отличие от рассмотренных в лабораторной работе №3 линейных электрических цепей первого порядка, переходные процессы в цепях второго порядка описываются линейными дифференциальными уравнениями второго порядка. Общий вид таких уравнений:
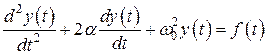, (4.1)
где 
- реакция электрической цепи, а 
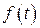- функция, определяемая задающими токами и ЭДС источников, действующих на цепь. Коэффициенты 
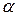и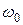 
носят названия коэффициента затухания и частоты незатухающих колебаний. Главной особенностью переходных процессов в линейных электрических цепях второго порядка является зависимость типа переходного процесса от соотношения между введенными коэффициентам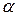и, и 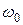. Различают три типа переходных процессов: апериодический, критический и колебательный. Вид свободной составляющей реакции определяется, как и в случае линейных электрических цепей первого порядка, корнями характеристического уравнения, которое в данном случае имеет вид:
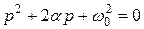. (4.2)
Вид корней этого уравнения определяется его дискриминантом.
|
|
|
1. Если дискриминант характеристического уравнения положителен, а это соответствует неравенству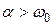 
, то корни этого уравнения оказываются вещественными, разными, отрицательными. Свободная составляющая реакции цепи в этом случае определяется выражением:
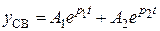, (4.3)
где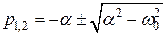 
. Говорят, что переходной процесс в этом случае носит апериодический характер.
2. Если дискриминант характеристического уравнения равен нулю, что выполняется при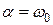 
, то корни характеристического уравнения оказываются вещественными, одинаковыми, отрицательными. В этом случае свободная составляющая может быть записана в виде:
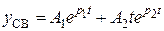, (4.4)
где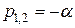 
. Характер переходного процесса в этом случае - критический.
3. Если дискриминант характеристического уравнения отрицателен, что возможно только при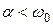 
, то корни характеристического уравнения оказываются комплексно сопряженными с отрицательной вещественной частью. Общий вид свободной составляющей реакции цепи в этом случае такой же, как и для апериодического переходного процесса:
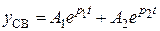, (4.5)
где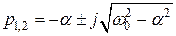 
[1]. Тип переходного процесса в этом случае – колебательный.
Однако, это не единственная форма представления свободной составляющей реакции для колебательного переходного процесса. Выражение (4.5) может быть также сведено к тригонометрической форме[2]:
|
|
|
(4.6)
где введено обозначение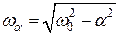 
.
Из выражения (4.6) непосредственно виден физический смысл введенных коэффициентов. Коэффициент 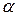есть ни что иное, как относительная скорость уменьшения амплитуды колебаний. Величина 
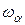описывает частоту затухающих колебаний. Если 
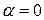, то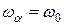 
, а значит, 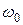имеет смысл частоты незатухающих колебаний.
Помимо введенного коэффициента затухания 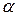изменение амплитуды колебаний можно характеризовать так называемыми линейным и логарифмическим декрементами затухания 
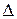и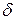 
. Физический смысл этих величин можно пояснить с помощью рис. 4.1, иллюстрирующего свободную составляющую реакции электрической цепи в колебательном переходном процессе.
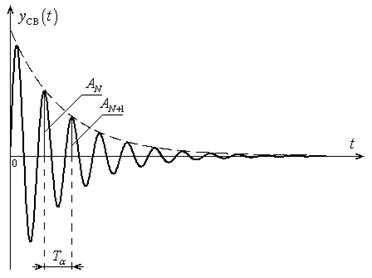
Рис. 4.1
Под линейным декрементом затухания понимают отношение двух амплитуд свободных колебаний, отстоящих друг от друга по времени на величину периода затухающих колебаний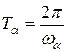 
:
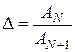. (4.7)
Из выражения (4.6) видно, что:
.
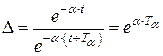Логарифмический декремент связан с линейным декрементом затухания выражением:
. (4.8)
|
|
|
Простейшей цепью второго порядка является последовательное соединение источника ЭДС, сопротивления, индуктивности и емкости, известное как последовательный колебательный контур. Важнейшей характеристикой такой цепи является добротность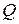 
, определяемая как отношение энергии, запасаемой в системе к энергии потерь в ней за период колебаний, умноженной на 
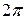. Эта величина также связана с затуханием колебаний и может быть оценена по графику свободной составляющей реакции цепи как число полных различимых колебаний.
Из выражений (4.4)-(4.7) видно, что отыскание реакции цепи сопровождается определением двух констант интегрирования (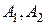 
или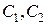 
). Это возможно, если известны два начальных условия, в качестве которых принято выбирать значение реакции и ее производной в момент времени 
.
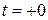Рассмотрим различные типы переходных процессов на конкретных примерах.
Пример 1
Рассмотрим переходный процесс в линейной электрической цепи второго порядка, вызванный подключением источника постоянной ЭДС к последовательно соединенным сопротивлению, индуктивности и ёмкости (рис. 4.2), выбрав в качестве реакции напряжение на емкости.
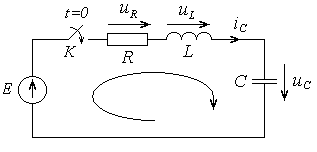
Рис. 4.2
Рассмотрим переходной процесс в цепи, составив дифференциальное уравнение для искомой реакции. Поскольку цепь не содержит узлов, а представляет собой контур, то достаточно составить одно уравнение по второму закону Кирхгофа, дополнив его компонентными соотношениями:
|
|
|
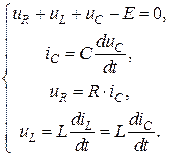(4.9)
Подставим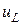 
и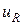 
в первое уравнение. Получим:
(4.10)
Подстановка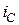 
в первое уравнение с последующим его делением почленно на 
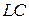приводит к дифференциальному уравнению вида:
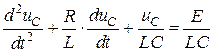. (4.11)
Введем обозначения:
, 
.
Пусть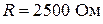 
, 
, 
, 
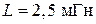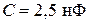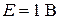. Тогда:
, 
.
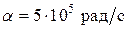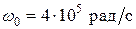Поскольку 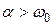, то переходной процесс носит апериодический характер и свободная составляющая реакции 
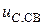запишется в виде:
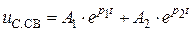, (4.12)
где:
,
.
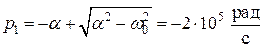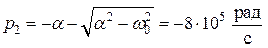Вынужденную составляющую реакции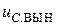 
определим, исключив обе производные из дифференциального уравнения (4.11):
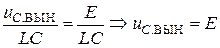. (4.13)
Тогда общее решение уравнения (4.11) имеет вид:
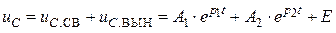. (4.14)
Найдем независимые и зависимые начальные условия. В момент времени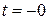 
источник ЭДС был отключен от цепи и, следовательно:
, 
.
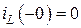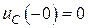Согласно законам коммутации:
, 
.
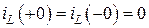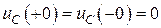Поскольку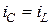 
, то и 
.
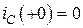Определим константы интегрирования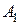 
и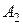 
исходя из начальных условий для 
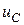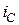и . С этой целью запишем общее выражение для тока 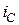, воспользовавшись уравнение (4.13) и вторым уравнением исходной системы (4.9):
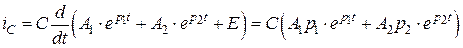. (4.15)
Подставляя начальные условия в (4.14) и (4.15) получим следующую систему для определения 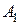и :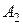
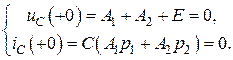(4.16)
Выразим 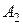из первого уравнения и подставим его во второе. Получим:
, 
.
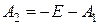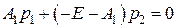Следовательно:
, 
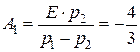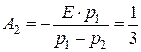. (4.17)
С учетом найденных констант интегрирования искомая реакция принимает вид:
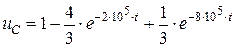. (4.18)
На рис. 4.3 представлен график зависимости найденной реакции от времени:
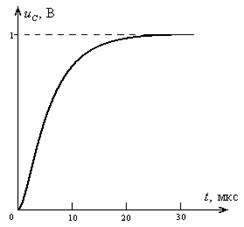
Рис. 4.3
Пример 2
Рассмотрим переходной процесс в линейной электрической цепи второго порядка, вызванный подключением ветви, содержащей емкость (рис. 4.4). Выберем в качестве реакции ток, протекающий через емкость. Однако задачу проще решить, если сначала найти выражение, описывающее изменение напряжения на емкости, а затем воспользоваться компонентным соотношением.
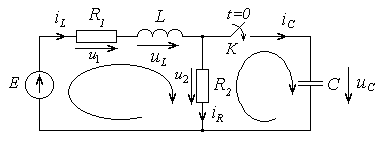
Рис. 4.4
Данная цепь содержит два узла и три ветви. Следовательно, по первому закону Кирхгофа достаточно составить одно уравнение и по второму закону Кирхгофа – два уравнения[3]. Дополним эти уравнения компонентными соотношениями. Полученная система уравнений имеет вид:
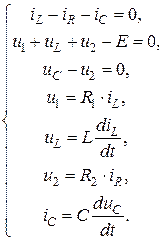(4.19)
Сведем данную систему уравнений к дифференциальному уравнению для напряжения на емкости. С этой целью подставим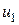 
, 
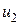и 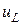во второе и третье уравнения. Получим:
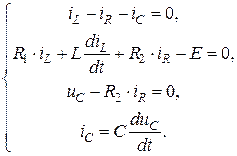(4.20)
Выразим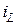 
из первого уравнения и подставим во второе. Получим систему из трех уравнений вида:
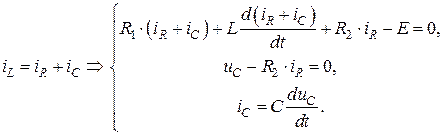(4.21)
Следующим шагом исключим из системы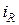 
. Для этого выразим его из второго уравнения и подставим в первое. Получим:
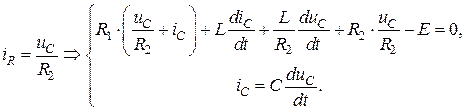(4.22)
Подставим 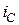в первое уравнение, приведем подобные и разделим все уравнение на 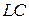. Получим:
. (4.23)
Введем принятые выше обозначения:
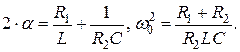
Пусть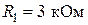 
, 
, 
, 
, 
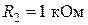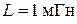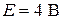. Тогда:
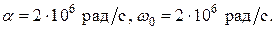
Поскольку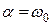 
, то характер переходного процесса – критический. Значит, свободная составляющая напряжения на емкости 
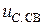равна:
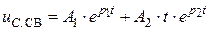, (4.24)
где:
.
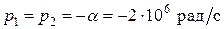Вынужденную составляющую напряжения на емкости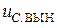 
найдем, исключив обе производные из дифференциального уравнения (4.23):
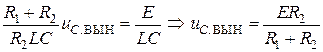. (4.25)
Тогда общее решение уравнения (4.23) имеет вид:
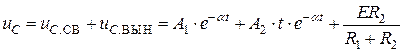. (4.26)
Для определения констант интегрирования 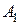и 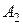найдем зависимые и независимые начальные условия. Рассмотрим цепь в момент времени 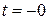, предшествующий замыканию ключа (рис. 4.5).
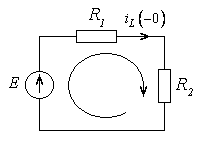
Рис. 4.5
Согласно второму закону Кирхгофа для данной цепи:
.
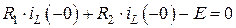Следовательно:
.
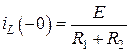Поскольку емкость была отключена от цепи, то напряжение на ней равнялось нулю:
.
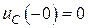Согласно законам коммутации:
, .
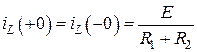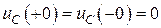Рассмотрим цепь в момент времени 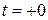, следующий сразу за замыканием ключа, и определим зависимое начальное условие 
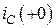(рис. 4.6).
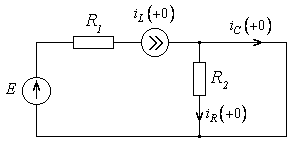
Рис. 4.6
Поскольку сопротивление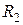 
в данной схеме оказывается закороченным, то напряжение на нем равно нулю, а значит, согласно закону Ома, и ток 
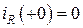. Следовательно, так как разветвления тока источника 
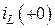не происходит, то:
.
Запишем общее выражение для тока 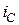, воспользовавшись (4.26) и компонентным соотношением для емкости:
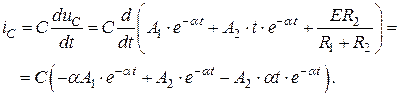(4.27)
Подстановка найденных начальных условий в (4.26) и (4.27) дает следующую систему уравнений для нахождения 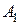и :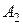
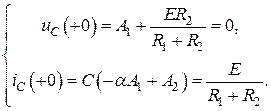(4.28)
Решая эту систему, находи, что:
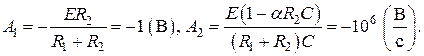
Тогда напряжение на емкости и ток, протекающий через нее, имеют вид:
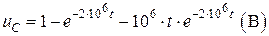, (4.29)
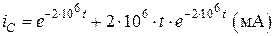. (4.30)
На рис. 4.7 представлен график изменения тока 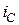со временем.
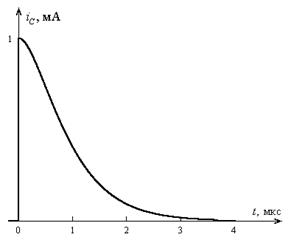
Рис. 4.7
Пример 3
Рассмотрим переходный процесс в линейной электрической цепи второго порядка, вызванный подключение ветви, содержащей сопротивление 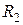и емкость 
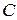(рис. 4.8), выбрав в качестве реакции ток 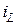, протекающий через индуктивность.
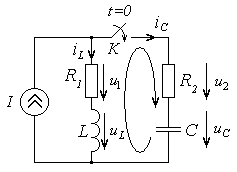
Рис. 4.8
Поскольку цепь содержит два узла и три ветви, то для описания протекающих в ней процессов необходимо записать одно уравнение по первому закону Кирхгофа и два – по второму. Однако один из токов ветвей является задающим током источника и считается известным. Следовательно, по второму закону Кирхгофа будет составлено лишь одно уравнение. Дополним систему компонентными соотношениями. Получим:
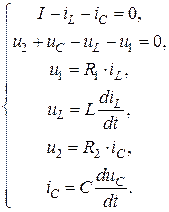(4.31)
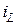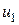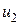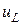Сведем систему (4.31) к дифференциальному уравнению для тока . С этой целью подставим выражения для , и во второе уравнение системы. Получим:
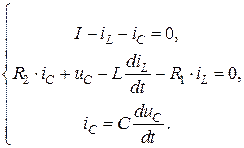(4.32)
Выразим ток 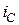из первого уравнения и подставим во второе и третье:
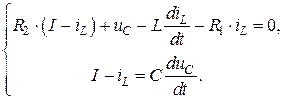(4.33)
Выразим 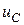из первого уравнения и подставим во второе. После приведения подобных и деления всего уравнения почленно на 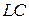получим:
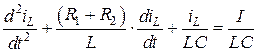. (4.34)
Введем обозначения:
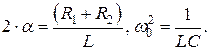
Пусть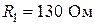 
, 
, 
, 
, 
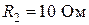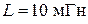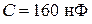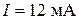. Тогда:
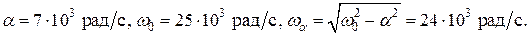
Поскольку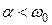 
, то характер переходного процесса – колебательный. Значит свободная составляющая тока, протекающего через индуктивность 
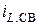равна:
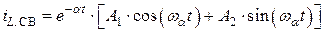, (4.35)
Вынужденную составляющую тока, протекающего через индуктивность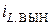 
, найдем, исключив обе производные из дифференциального уравнения (4.34):
. (4.36)
Тогда общее решение уравнения (4.34) имеет вид:
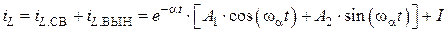. (4.37)
Для определения констант интегрирования 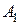и 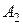найдем зависимые и независимые начальные условия. Рассмотрим цепь в момент времени 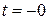, предшествующий замыканию ключа (рис. 4.9).
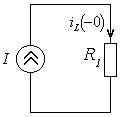
Рис. 4.9
Поскольку цепь одноконтурная, то элементы соединены последовательно и во всей цепи протекает один и тот же ток, равный задающему току источника:
.
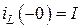Поскольку до замыкания ключа емкость была отключена, то напряжение на ней:
.
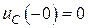Тогда согласно законам коммутации:
, .
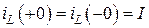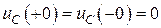Рассмотрим цепь в момент времени 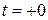, следующий сразу за замыканием ключа, и определим зависимое начальное условие 
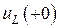(рис. 4.10).
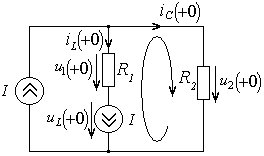
Рис. 4.10
Поскольку в цепи действует два источника, то суммарное напряжение 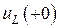найдем как сумму напряжени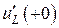й 
и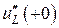 
, отражающих реакцию цепи на действие каждого из источников в отдельности (метод наложения). Поочередное гашение источников тока приводит к цепям, изображенным на рис. 4.11.
Рис. 4.11
Для цепи на рис. 4.11, а ток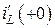и 
и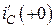 
имеют одинаковое абсолютное значение, равное задающему току источника, но противоположны по направлению. Значит, второй закон Кирхгофа для этой одноконтурной цепи имеет вид:
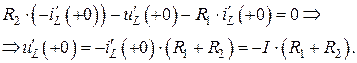
Для цепи на рис. 4.11, б ток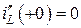 
, а ток 
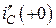согласно первому закону Кирхгофа равен задающему току источника 
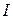. Тогда уравнение, составленное по второму закону Кирхгофа для выбранного контура, имеет вид:
.
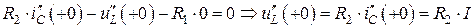Тогда зависимое начальное условие для напряжения на емкости:
.
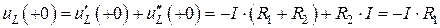Запишем общее выражение для напряжения 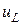, воспользовавшись (4.37) и компонентным соотношением для индуктивности:
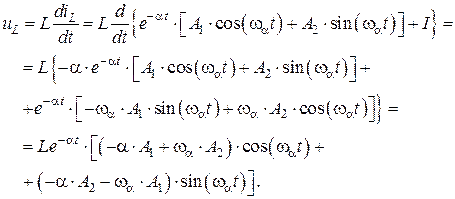(4.38)
Подстановка найденных начальных условий в (4.37) и (4.38) дает следующую систему уравнений для нахождения 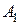и :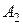
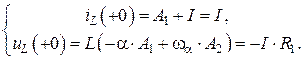(4.39)
Из первого уравнения системы (4.39) находим, что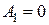 
. Тогда из второго уравнения следует, что 
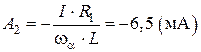. Тогда ток, протекающий через индуктивность, имеет вид:
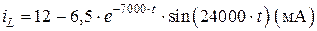. (4.40)
На рис. 4.12 представлен график изменения тока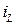 
со временем.
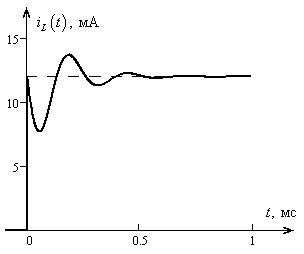
Рис. 4.12
Описание лабораторной установки
В состав лабораторной установки входят: генератор стандартных сигналов, электронный осциллограф и лабораторный макет с набором необходимых элементов. Каждая бригада, получив задание, монтирует исследуемые цепи на наборной плате макета с помощью перемычек.
Задание на самоподготовку
В соответствии с исходными данными (табл.1) рассчитать постоянные времени RC и RL-цепей для двух значений сопротивления. Вычислить длительность переходного процесса, длительность импульса и частоту их следования, необходимые для наблюдения импульсных и переходных характеристик всех исследуемых цепей (см. бланк отчета).
Таблица 1.
| Номер бригады | Вид переходного процесса | L, мГн | C, нФ | R, Ом |
| 1 | Апериодический | 3,1 | 4,6 | 200 |
| Колебательный | 1000 | |||
| 2 | Апериодический | 15 | 29 | 270 |
| Колебательный | 6200 | |||
| 3 | Апериодический | 44 | 43 | 270 |
| Колебательный | 6200 |
Лабораторное задание
1. Подготовить измерительные приборы к работе, включить их.
2. Смонтировать на макете последовательный апериодический RLC-контур.
3. Снять осциллограммы свободных и переходных колебаний напряжения на емкости (импульсных и переходных характеристик) последовательной RLC-цепи в апериодическом режиме.
4. Определить по осциллограммам значения рассчитанных в п. 1.3 числовых параметров и сравнить их с расчетными значениями.
5. Смонтировать на макете последовательный колебательный RLC-контур.
6. Снять осциллограммы свободных и переходных колебаний напряжения на емкости (импульсных и переходных характеристик) последовательной RLC-цепи в колебательном режиме.
7. Определить по осциллограммам значения рассчитанных в п. 1.3 числовых параметров и сравнить их с расчетными значениями.
Содержание отчета
1. Цель работы.
2. Схемы исследуемых цепей и расчеты при самоподготовке.
3. Функциональная схема лабораторной установки.
4. Результаты экспериментального исследования (осциллограммы и необходимые вычисления).
5. Сравнение результатов расчета и эксперимента и выводы.
Контрольные вопросы
1. Какая линейная электрическая цепь называется цепью второго порядка? Привести примеры.
2. В чем состоит особенность поиска начальных условий для цепи второго порядка?
3. Какие режимы переходного процесса возможны в цепи второго порядка, и при каких условиях (три формы условий) они возникают?
4. Перечислите свойства корней характеристического уравнения в различных режимах переходного процесса.
5. Как записывается свободная составляющая реакции цепи в каждом из режимов переходного процесса?
6. Дайте определение коэффициента затухания, частоты собственных незатухающих колебаний и частоты собственных затухающих колебаний. Как их определить из дифференциального уравнения цепи?
7. Дайте определение линейного декремента затухания. Как определить линейный декремент из графика свободных колебаний? Как связаны линейный и логарифмический декременты затухания?
8. Как определяется длительность переходного процесса в различных режимах и от чего она зависит?
9. Дайте определение добротности последовательного RLC-контура. Покажите, что число полных наблюдаемых колебаний в графике свободных колебаний определяется величиной добротности.
Литература
1. Крюков И.Н., Шрейдер Б.Г., Щепеткин Ф.В. Основы теории цепей. - КВИ ФПС. Калининград 1998.
2. Баскаков С.И. Лекции по теории цепей. -М.: МЭИ, 1991.
3. Матханов П.Н. Основы анализа линейных электрических цепей. -М.: Высшая школа, 1987.
[1] Здесь и далее символом обозначена мнимая единица . Символ не применяется, так как он используется для обозначения тока.
[2] Для этого необходимо воспользоваться формулами Эйлера: ,
[3] Смотри примеры решения задач на переходные процессы в линейных электрических цепях первого порядка.
Дата добавления: 2021-03-18; просмотров: 52; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!